Video Lecture
Theory For Making Notes
Induced Emf In A Rotating Coil
Suppose a rectangular coil having N turns placed initially in a magnetic field such that magnetic field is perpendicular to it’s plane as shown.
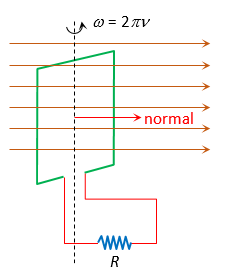
\displaystyle \omega – Angular speed , where \displaystyle \omega =\frac{\theta }{t}\text{ also }\omega =2\pi \upsilon
\displaystyle \nu – Frequency of rotation of coil
R – Resistance of coil
For uniform rotational motion with angular velocity \displaystyle \omega , the flux linked with coil at any time t
\phi =NBA\cos \theta =NBA\cos \omega t here \displaystyle \theta is the angle between normal to coil and the magnetic field
\phi ={{\phi }_{0}}\cos \,\omega t where \displaystyle {{\phi }_{o}}=NBA= maximum flux
Using Faraday’s law we can find the Induced emf in the coil as follows
E=-\frac{{d\phi }}{{dt}}=-NBA\frac{d}{{dt}}(\cos \omega \,t)=NBA\omega \sin \omega \,t
\displaystyle \Rightarrow E={{E}_{0}}\sin \omega t
Where \displaystyle {{E}_{0}} = emf amplitude or max. emf =NBA\omega ={{\phi }_{0}}\omega
The equation shows that the emf changes in periodic manner that’s why this phenomenon is also called periodic EMI
Induced current in the coil can be found using ohm’s law as follows
At any time t, I=\frac{E}{R}=\frac{{{{E}_{0}}}}{R}\sin \omega \,t={{I}_{0}}\sin \omega \,t
where \displaystyle {{I}_{0}} = current amplitude or max. current {{I}_{0}}=\frac{{{{E}_{0}}}}{R}=\frac{{NBA\omega }}{R}=\frac{{{{\phi }_{0}}\omega }}{R}
Note that the flux depends on \displaystyle cos\theta whereas the emf depends on \displaystyle sin\theta , hence there exist a phase difference of \displaystyle {{90}^{o}} between them, this means that when the flux passing through the coil is maximum the emf induced in it is zero and vise versa
AC Generator
An electrical machine used to convert mechanical energy into electrical energy is known as ac generator/alternator.
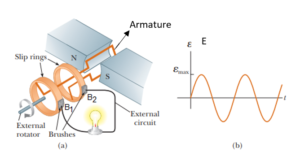
Principle : It works on the principle of electromagnetic induction i.e., when a coil is rotated in uniform magnetic field, an induced emf is produced in it.
Construction : The main components of ac generator are
(i) Armature : Armature coil consists of large number of turns of insulated copper wire wound over a soft iron core.
(ii) Strong field magnet : A strong permanent magnet or an electromagnet whose poles (N and S) are cylindrical in shape in a field magnet. The armature coil rotates between the pole pieces of the field magnet. The uniform magnetic field provided by the field magnet is perpendicular to the axis of rotation of the coil.
(iii) Slip rings : The two ends of the armature coil are connected to two brass slip rings . These rings rotate along with the armature coil.
(iv) Brushes : Two carbon brushes, are pressed against the slip rings. The brushes are fixed while slip rings rotate along with the armature. These brushes are connected to the load through which the output is obtained.
Working : When the armature coil rotates in the magnetic field provided by the strong field magnet, it cuts the magnetic lines of force. Thus the magnetic flux linked with the coil changes and hence induced emf is set up in the coil. The direction of the induced emf or the current in the coil is determined by the Fleming’s right hand rule.
The current flows out through the brush \displaystyle {{B}_{1}} in one direction of half of the revolution and through the brush \displaystyle {{B}_{2}} in the next half revolution in the reverse direction. This process is repeated. Therefore, emf produced is of alternating nature.
E=-\frac{{Nd\phi }}{{dt}}
hence, E =NBA\omega \sin \omega t
\displaystyle \Rightarrow E={{E}_{0}}\sin \omega t where \displaystyle {{E}_{0}}=NBA\omega
I=\frac{E}{R}=\frac{{{{E}_{0}}}}{R}\sin \omega t={{I}_{0}}\sin \omega t R =Resistance of the circuit
ILLUSTRATION
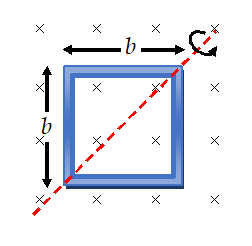
A single square loop of side b=20cm is rotated in a constant magnetic field B=2T at frequency 50Hz as shown. What is the maximum emf induced in it? Also write the equation of instantaneous emf induced in it. State will the emf change if the loop is rotated about one of its sides?
Solution :
As discussed in the topic given above the induced emf in the rotating coil is given by E={{E}_{0}}\sin \,\omega t, where \displaystyle {{E}_{0}}=NBA\omega
In this question N=1 , B= 2T,
A= 20 x 20 \displaystyle =\text{ }400\text{ }c{{m}^{2}}=\text{ }4\times {{10}^{{-2}}}{{m}^{2}}~,
\displaystyle \omega \text{ }=\text{ }2\pi \nu =\text{ }2\times \pi \times 50\text{ }=\text{ }100\pi rad/sec
Hence maximum emf \displaystyle {{E}_{0}}=NBA\omega
i.e. \displaystyle =\text{ }1\times 2\times 4\times {{10}^{{-2}}}\times 100\pi \text{ }=\text{ }8\text{ }\pi volt
Equation of instantaneous emf induced in it is E={{E}_{0}}\sin \,\omega t
Hence \displaystyle E=8\pi sin(100\pi t)
If the coil is rotating about any side the emf remains the same as it depends on magnitude of area, angular velocity, magnetic field and the number of turns. As long as these quantities remains same the emf remains same.
Practice Questions (Basic Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Main Level)
Q.1
A flat circular coil of n turns, area A and resistance R is placed in a uniform magnetic field B. The plane of coil is initially perpendicular to B. When the coil is rotated through an angle of 180o about one of its diameter, a charge Q1 flows through the coil. When the same coil, after being brought to its initial position, is rotated through an angle of 360o about the same axis a charge Q2 flows through it. Then Q2/Q1 is
(a) 1 (b) 2 (c) 1/2 (d) 0
Ans. (d)
Q.2
A square loop of side b is rotated in a constant magnetic field B at angular frequency w as shown in the figure. What is the emf induced in it?
(a) b2Bw sin wt
(b) bBw sin2 wt
(c) bB2w cos wt
(d) b2Bw
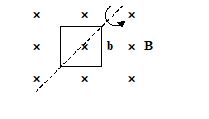
Ans. (a)
Q.3
If the flux of magnetic induction through a coil of resistance R and having n turns changes from f1 to f2, then the magnitude of the charge that passes through the coil is
(a) \frac{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}{R}
(b) \frac{{n\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}{R}
(c) \frac{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}{{nR}}
(d) \frac{{nR}}{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}
Ans. (b)
Q.4
A coil of 20×20 cm having 30 turns is making 30 rps in a magnetic field of 1 tesla. The peak value of the induced e.m.f. is approximately
(a) 452 V (b) 226 V (c) 113 V (d) 339 V
Ans. (b)
Q.5
In a uniform magnetic field of induction B, a wire in the form of semicircle of radius r rotates about the diameter of the circle with angular frequency w. If the total resistance of the circuit is R, the mean power generated per period of rotation is
(a) \frac{{B\pi {{r}^{2}}\omega }}{{2R}}
(b) \frac{{{{{(B\pi {{r}^{2}}\omega )}}^{2}}}}{{2R}}
(c) \frac{{{{{(B\pi r\omega )}}^{2}}}}{{2R}}
(d) \frac{{{{{(B\pi {{r}^{2}}\omega )}}^{2}}}}{{8R}}
Ans. (d)
Practice Questions (JEE Advance Level)
Q.1
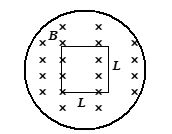
Figure shows a square loop of side L perpendicular to the uniform field of a solenoid. Evaluate \oint{{\vec{E}}}. d \vec{l} around the loop.
(a) 4L\frac{{dB}}{{dt}}
(b) 2{{L}^{2}}\frac{{dB}}{{dt}}
(c) L\frac{{dB}}{{dt}}
(d) {{L}^{2}}\frac{{dB}}{{dt}}
Ans : (d)
Q.2
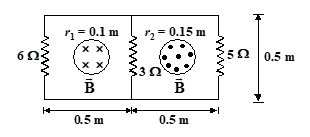
Two infinitely long solenoids (shown in cross-section) pass through a circuit as shown in the figure.
100 T/s. The current in 6ohm, 5ohm and 3ohm resistors are respectively
(a) 0.06A, 0.85A, 0.91A
(b) 2.06A, 1.85A,1.91A
(c) 0.06A, 2.85A,3.91A
(d) 1.06A, 0.85A,2.91A
Ans : (a)