Video Lecture
Theory For Notes Making
Electric Lines of Force
The lines of forces are purely geometrical construction which helps in visualising the nature of electric field in a region. It has no physical existence. Lines of forces are drawn in such a way that the tangent to a line of force gives the direction of resultant electric field. The density of field lines in any region is proportional to the magnitude of the electric field in that region. Field lines originate on positive charges and terminate on negative charges.
1.
There cannot be any closed line of force in an electrostatic field \displaystyle \vec{E}. Electric lines of force emerge from positive charges and terminate on negative charges (or extends to infinity).

2.
Crowded lines represent strong field, while distant represent weak field.
3.
The number of lines originating or terminating on a charge is proportional to the magnitude of the charge. In SI units, the number of electric field lines associated with a unit charge (i.e., 1 coulomb) is taken as 1/ε0. Thus, if a body encloses a charge q, total lines of force associated with it (also called flux) will be q/ε0.
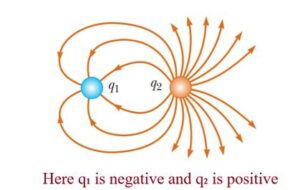
In the above figure the magnitude of q2 is more than that of q1.
4.
Lines of force can never cross each other. It is obvious, because if they cross at a point the intensity at that point will have two directions, which is absurd.
5.
Lines of force have tendency to contract longitudinally (like a stretched elastic string) and repel each other laterally. This concept, like the lines of force, is also imaginary. It helps in understanding how attraction is produced between opposite charges, and how repulsion is produced between similar charges.

Electric field lines for two positive point-charges of equal magnitude.

Electric field lines of two similar charges placed near to each other
6.
If there is no electric field in a region of space, there will be no lines of force. This is why inside a conductor or at a neutral point (where resultant intensity is zero) there cannot be any line of force.
7.
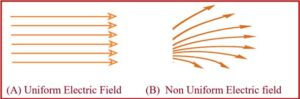
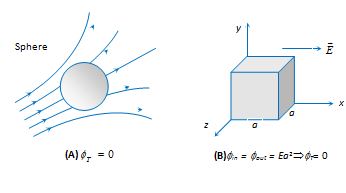
If the lines of force are equidistant straight lines, the field is uniform [Fig. (A)]. If either lines of force are not equidistant or straight lines or both, the field will be non-uniform [Fig. (B)]
Electric Flux
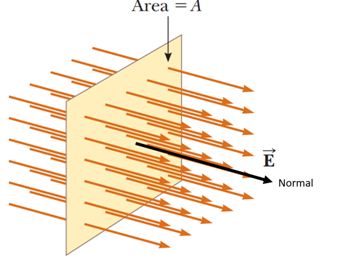
Consider a surface of area A placed in an electric field E.
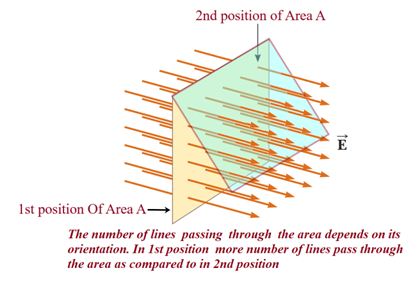
Now the number of lines that penetrate through the surface depends on three factors
(i) Strength of electric field E
(ii) Surface area A
(iii) Orientation of area with respect to the electric field .
If N is the number of electric field lines passing through the Area then
\displaystyle N\propto \vec{E} —————(i)
And \displaystyle N\propto \vec{A} —————(ii)
On combining (i) and (ii) we get
\displaystyle N\propto \vec{E}.\vec{A}
Here the term \displaystyle \vec{E}.\vec{A} is called electric flux and is denoted by \displaystyle \phi .
So we can define electric flux as the dot product of electric field vector and area vector.
The number of electric field lines passing through the surface area depends on the electric flux.
Hence \displaystyle \phi =\vec{E}.\vec{A}
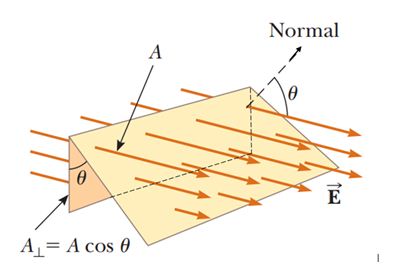
Or \displaystyle \phi =EA\cos \theta .
Here \displaystyle A\cos \theta is denoted by \displaystyle {{A}_{\bot }} and it is the projection of area A onto a plane oriented perpendicular to the electric field as shown in the diagram given below and \displaystyle \theta is the angle between electric field vector and normal to the area.
Note that
- SI units of \displaystyle \phi is N.m2/C.
- \displaystyle \phi is a scalar quantity.
From the equation \displaystyle \phi =EA\cos \theta we can conclude the following important points
(i)
when θ = 0 that is the normal to area is parallel to the electric field or the plane of the area is perpendicular to the field , the flux through the area is maximum
(ii)
When θ =90o the flux passing through the area is zero.

(iii)
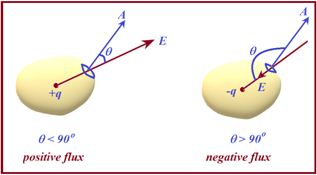
Concept of positive and negative flux
In case of closed surface the flux may be positive or negative depending on the direction of field lines and the angle between the normal and the electric field as shown in the diagram given below. In the diagram there are two close surfaces. The first one contains a positive charge and the second contains a negative charge. In the first case the angle between the normal to surface and the electric field is less than 90o. So according to formula \displaystyle \phi =EA\cos \theta , the flux is positive. whereas in the second case the flux is negative because θ is more than 90o.
(iv)
For a closed body outward flux is taken to be positive as shown in fig. (A) while inward negative as shown in fig. (B)

(v)
The electric flux is contributed by only that charge which is enclosed by the surface. If a charge is lying outside the closed surface the net electric flux passing the closed surface is zero whereas electric field is produced by all the charges whether inside on outside.
Gauss Theorem
The statement of the Gauss’s law may be written as follows :
The flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ε0.
Mathematically it can be written as
\displaystyle \oint\limits_{{surface}}{{\overrightarrow{E}\,\cdot \,\overrightarrow{{dS}}}}\,\,=\,\,\frac{{{{q}_{{in}}}}}{{{{\varepsilon }_{0}}}} …(i)
where qin is the net charge enclosed by the surface through which the flux is calculated.
It should be carefully noted that the electric field on the left-hand side of equation (i) is the resultant electric field due to all the charges existing in the space, whereas, the charge appearing on the right-hand side includes only those which are inside the closed surface.
Derivation of Gauss’s Theorem
Consider a charge q . Construct a spherical surface around it with charge at the center. Now the flux passing through the spherical surface is same as that produced by the charge.
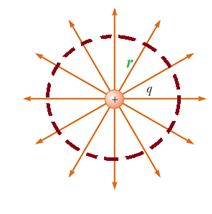
The flux passing through the spherical surface can be calculated using the equation \displaystyle \phi =EA\cos \theta .
here E is the electric field produced by the charge hence \displaystyle E=\frac{{kq}}{{{{r}^{2}}}},
A is the surface area of the sphere hence \displaystyle A=4\pi {{r}^{2}}
and \displaystyle \theta = 0 as the electric field is radial hence it is along the normal to the surface.
So \displaystyle \phi =\frac{{kq}}{{{{r}^{2}}}}.4\pi {{r}^{2}}.\cos (0)=kq4\pi
\displaystyle \Rightarrow \phi =\frac{1}{{4\pi {{\varepsilon }_{o}}}}q4\pi
hence \displaystyle \phi =\frac{q}{{{{\varepsilon }_{o}}}}
This is the flux passing through the spherical surface and actually it is produced by the charge q place at the center. So we conclude that a charge q produce a total flux equal to \displaystyle \frac{q}{{{{\varepsilon }_{o}}}}.
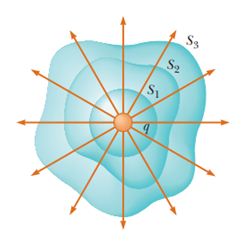
Hence if a charge is surrounded by a number of closed surfaces of any shape as shown then the flux passing through every surface is equal to that produced by the charge i.e. \displaystyle \frac{q}{{{{\varepsilon }_{o}}}}.
Application of Gauss’s Law
Using Gauss’s law in some cases with symmetry arguments, we can derive several important results in electrostatic situations.
(For detailed derivation please see the video lectures)
1.
The electric field at any point due to an infinite line of charge with uniform linear charge density \lambda is perpendicular to the line of charge and has magnitude
E=\frac{\lambda }{{2\pi {{\varepsilon }_{o}}r}} (line of charge)
where r is the perpendicular distance from the line of charge to the point.
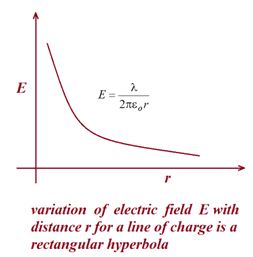
2.
The electric field due to an infinite nonconducting sheet with uniform surface charge density σ is perpendicular to the plane of the sheet and has magnitude
E=\frac{\sigma }{{2{{\varepsilon }_{o}}}} (sheet of charge)
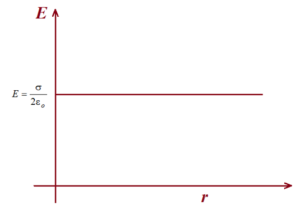
Note that this electric field does not depend on the distance r from the sheet,hence it is a constant.
3.
The electric field outside a spherical shell of charge with radius R and total charge q is directed radially and has magnitude
E=\frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{q}{{{{r}^{2}}}} (spherical shell, for r ≥ R).
Here r is the distance from the center of the shell to the point at which E is measured. (The charge behaves, for external points, as if it were all located at the center of the sphere).
The field inside a uniform spherical shell of charge is exactly zero.
hence for a spherical shell E=0 ( for r<R).
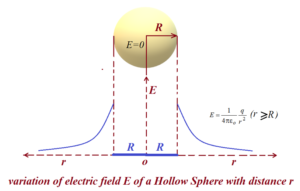
4.
The electric field inside a uniformly charged non conducting sphere is directed radially and has magnitude
E=\left( {\frac{q}{{4\pi {{\varepsilon }_{o}}{{R}^{3}}}}} \right)r=\frac{{\rho r}}{{3{{\varepsilon }_{o}}}}
where as outside it is given as E=\frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{q}{{{{r}^{2}}}}

Illustration
A spherical shell of radius a is placed in a uniform electric field \displaystyle \vec{E}. Find the amount of flux entering into the shell

Solution
It is the shaded circular area or projected area of shell which is intercepting the flux hence flux entering depends on this area
\phi=E.S=E.\pi {{a}^{2}}
Illustration
Determine the field at a point distant \rho from a uniformly charged plane with surface charge density \sigma .

Solution
By symmetry, we conclude the \displaystyle \overrightarrow{E} can only be normal to the charged plane. Also, at points A and B, symmetric with respect to the plane, \displaystyle \overrightarrow{E} should have same magnitude but opposite directions. Hence, a right cylinder is chosen as Gaussian surface.
The flux through the lateral surface is zero. If \displaystyle \Delta S is the area of each end face,the total flux is
\displaystyle \Delta \phi \text{ }=E\Delta S+E\Delta S=\text{ }2E\Delta S
Then according to Gauss’s Law,
2E \Delta S = \frac{{{{q}_{{in}}}}}{{{{\varepsilon }_{0}}}}\text{ }=\text{ }\frac{{\sigma \Delta S}}{{{{\varepsilon }_{0}}}}
\displaystyle E=\frac{\sigma }{{2{{\varepsilon }_{0}}}}
Illustration
A uniform positive charge density \rho (charge per unit volume) exists throughout a spherical volume of radius R. Find the electric field (a) outside the sphere and (b) inside the sphere. Also show how electric field varies as the distance of the point from the centre increases from zero to infinite.
Solution
By symmetry, we conclude that the field \displaystyle \overrightarrow{E} can only be radially outward, both inside and outside the sphere. Moreover, for a given value of r, \displaystyle \overrightarrow{E} has the same magnitude everywhere. To match this symmetry, we choose a Gaussian surface in the form of a sphere of radius r, centred on the spherical volume.
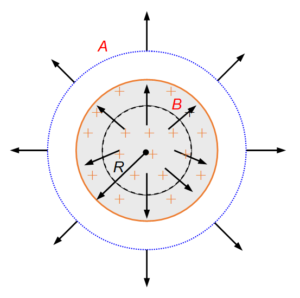
(a)
For any point outside the sphere, r > R :
The total charge inside the spherical volume (surface A) is
\displaystyle Q=\int{{\rho dV}}=\rho \left( {\frac{4}{3}\pi {{R}^{3}}} \right) …(i)
Applying Gauss’s Law,
\oint{{\vec{E}.d\vec{S}}} = \frac{{{{q}_{{\text{in}}}}}}{{{{\varepsilon }_{0}}}}
\displaystyle E(4\pi {{r}^{2}})=\frac{Q}{{{{\varepsilon }_{0}}}}
or \displaystyle E=\frac{Q}{{4\pi {{\varepsilon }_{0}}{{r}^{2}}}} …(ii)
This is just the inverse-square-law field for a point charge Q. In fact, this result is valid for any charged sphere, whether solid or hollow, conducting or non-conducting. The sphere behaves as if whole charge is concentrated at its centre. We can express the result of Eqn.(ii) in terms of the given parameters by using Eqn. (i),
\displaystyle E=\frac{Q}{{4\text{ }\pi {{\varepsilon }_{0}}{{r}^{2}}}}=\frac{1}{{4\text{ }\pi {{\varepsilon }_{0}}{{r}^{2}}}} \rho \left( {\frac{4}{3}\pi {{R}^{3}}} \right)=\frac{{\rho {{R}^{3}}}}{{3\text{ }{{\varepsilon }_{0}}}} \frac{1}{{{{r}^{2}}}}
i.e. E ∝ \displaystyle \frac{1}{{{{r}^{2}}}}
(b)
For any point inside the sphere (r<R) :
We now choose a Gaussian surface B, so that r<R. The charge inside this sphere is
\displaystyle {{q}_{{in}}} = \int\limits_{0}^{r}{{\rho dV}} = \rho \left( {4\text{/3 }\pi {{r}^{3}}} \right)
Applying Gauss’s law,
\displaystyle \oint{{\overrightarrow{E}\,\,.\,\,d\overrightarrow{S}}} = \frac{{{{q}_{{in}}}}}{{{{\varepsilon }_{0}}}}
or \displaystyle E(4\text{ }\pi \text{ }{{r}^{2}})\text{ }=\text{ }\frac{{4\text{ }\rho \text{ }\pi \text{ }{{r}^{3}}}}{{3{{\varepsilon }_{0}}}}
or E = \displaystyle \frac{\rho }{{3{{\varepsilon }_{0}}}}r
i.e. E ∝ r
Thus, inside the sphere of uniform charge, the field is directly proportional to the distance r from the centre. The variation of E with distance r is shown in the figure.

Some important Cases
(1)
If a closed body (not enclosing any charge) is placed in an electric field (either uniform or non-uniform) total flux linked with it will be zero
(2)
If a hemispherical body is placed in uniform electric field then flux linked with the curved surface calculated as follows
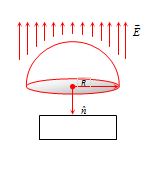
{{\phi }_{{Curved face}}}+{{\phi }_{{Circular face}}}=0
{{\phi }_{{Curved face}}}=-{{\phi }_{{Circular face}}}
=-\,(E\times \pi {{R}^{2}}\cos 180{}^\circ )
=+\pi {{R}^{2}}E
(3)
If a hemispherical body is placed in non-uniform electric field as shown below. then flux linked with the circular surface calculated as follows
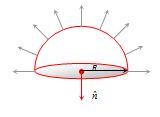
we know that in this ssituation the total flux passing through the hemisphere is zero.
So {{\phi }_{{(Circular face)}}}+{{\phi }_{{(Curved face)}}}=0
or {{\phi }_{{(Circular face)}}}=-{{\phi }_{{(Curved face)}}}
where {{\phi }_{{(Curved face)}}}= \,E\times 2\pi {{R}^{2}}\cos 0{}^\circ
therefore {{\phi }_{{(Circular face)}}}=-\,(E\times 2\pi {{R}^{2}}\cos 0{}^\circ )
so {{\phi }_{{(Circular face)}}}=-\,2\pi {{R}^{2}}E
(4)
If a charge is kept at the centre of cube, its total flux will pass through all 6 faces equally.
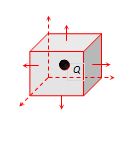
Hence {{\phi }_{{face}}= \frac{{{\phi }_{{total}}}}{6}}
where {{\phi }_{{total}}}=\frac{1}{{{{\varepsilon }_{0}}}}.(Q) (By Gauss’s Theorem)
Therefore {{\phi }_{{face}}}=\frac{Q}{{6{{\varepsilon }_{0}}}}
(5)
If charge is kept at the centre of a face as shown in fig.(A)
To find the flux passing through the cube first we should enclose the charge by assuming a Gaussian surface (an identical imaginary cube)as shown in fig.(B)
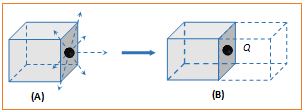
Total flux emerging from the system (Two cubes) {{\phi }_{{total}}}=\frac{Q}{{{{\varepsilon }_{0}}}}
Hence flux from the given cube (i.e. from 5 face only) {{\phi }_{{cube}}}=\frac{Q}{{2{{\varepsilon }_{0}}}}
(6)
If a charge is kept at the corner of a cube of edge length ‘a’ as shown in fig.(A). Then the flux passing through the cube can be found using Gauss’s theorem
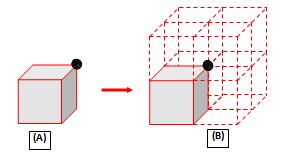
First enclose the charge by seven more cubes so that a bigger cube of side 2a can be made a shown in fig. (B). Now the given charge comes at the center of the bigger cube.
The total flux from the charge is {{\phi}_{T}}= \frac{Q}{{{{\varepsilon }_{0}}}}
This total flux is shared by all 8 cubes equally. Hence flux through one cube is one eighth of the total flux .
Therefore the flux from given cube is {{\phi }_{{cube}}}=\frac{Q}{{8{{\varepsilon }_{0}}}} .
Flux from one face opposite to charge, of the given cube is one third of the flux from the cube
Hence {{\phi }_{{face}}}=\frac {{{\phi }_{{cube}}}}{3}
so {{\phi }_{{face}}}=\frac{{Q/8{{\varepsilon }_{0}}}}{3}
Hence {{\phi }_{{face}}}=\frac{Q}{{24{{\varepsilon }_{0}}}} (Because only three faces will share the flux).
(7)
A long straight wire of charge density λ penetrates a hollow cube as shown below . The flux emerges from the cube is
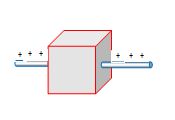
\displaystyle \phi = \lambda.x
(where x is the length of the wire inside the cube which is actually equal to the length of the edge of the cube )
Objective Assignment
Q.1
The electric field in a region of space is given by \overrightarrow{E}=5 \hat i+10 \hat j +20 \hat k N/C. The flux of due to this field through an area 2 m2 lying in the y-z plane, in SI units, is
(a) 10
(b) zero
(c) 10 \sqrt{2}
(d) 2 \sqrt{{29}}
Ans. (a)
Q.2
Figure shows a closed surface which intersects a conducting sphere. If a positive charged is placed at the point P, the flux of the electric field through the closed surface
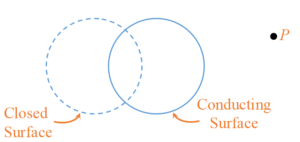
(a) will remain zero
(b) will become positive
(c) will become negative
(d) will become undefined
Ans. (b)
Q.3
In a region of space, an electric field is given as \overrightarrow{E}={{E}_{o}}.x \hat i . Consider an imaginary cubical volume of edge a, with its edges parallel to the axes of coordinates in this region. The charge inside this volume is
(a) zero
(b) {{\varepsilon}_{o}}{{E}_{o}}{{a}^{3}}
(c) \frac{1}{{{\varepsilon}_{o}}}{{E}_{o}}{{a}^{3}}
(d) \frac{1}{6{{\varepsilon}_{o}}}{{E}_{o}}{{a}^{2}}
Ans. (b)
Q.4
In a region of space, an electric field of 10 N/C acts in y-z plane at an angle of {{60}^{o}} with the +ve z axis. The electric flux through a surface of area of 100 units in x-y plane is
(a) 100 units
(b) 500 units
(c) 500 \sqrt{3} units
(d) 1500 units
Ans. (b)
Q.5
A cylinder of length L and radius b has its axis coincident with the y axis. The electric field in this region is \overrightarrow{E}=200 \hat j . Find the flux through the bottom surface of the cylinder.
(a) – 200 \pi {{b}^{2}}
(b) – 700 \pi {{b}^{2}}
(c) – 200bL
(d) 200 (\pi {{b}^{2}}+bL)
Ans: (a)
Q.6
Two oppositely charged parallel plates have dimensions of 10x20cm and have a charge of 20mC each. Find the electric flux and electric flux density between the two plates.
(a)0.25×106 Nm2/C , 0.125×108 N/C
(b) 25×106 Nm2/C , 125×108 N/C
(c) 2.25×106 Nm2/C , 1.125×108 N/C
(d)35×106 Nm2/C , 2×108 N/C
Ans: (c)
Q.7
A long string with a charge of \lambda per unit length passes through an imaginary cube of edge a. The maximum flux of the electric field through the cube will be
(a) \frac{{\lambda a}}{{{{\varepsilon }_{0}}}}
(b) \frac{{\sqrt{2}\,\lambda a}}{{{{\varepsilon }_{0}}}}
(c) \frac{{6\lambda {{a}^{2}}}}{{{{\varepsilon }_{0}}}}
(d) \frac{{\sqrt{3}\,\lambda a}}{{{{\varepsilon }_{0}}}}
Ans (d)
Q.8
A charge Q is located at the centre of a cube. The electric flux through any face of the cube is
(a) \frac{Q}{12{{\varepsilon}_{o}}}
(b) \frac{4\pi Q}{{{\varepsilon}_{o}}}
(c) \frac{Q}{6{{\varepsilon}_{o}}}
(d) \frac{Q}{4\pi {{\varepsilon}_{o}}}
Ans. (c)
Q.9
How many electrons must be added to a spherical conductor of radius 10 cm to produce a field of 2 \times {{10}^{-3}} N/C just above the surface
(a) 1.39 \times {{10}^{4}}
(b) 1.6 \times {{10}^{5}}
(c) 3 \times {{10}^{4}}
(d) 9.1 \times {{10}^{4}}
Ans. (a)
Q.10
A cylinder of radius R and length L is placed in a uniform electric field E applied parallel to the cylinder axis. The net flux passing through the surface of the cylinder is given by
(a) 2 \pi {{R}^{2}}E
(b) \frac {2 \pi {{R}^{2}}}{E}
(c) zero
(d) none of these
Ans. (c)
Q.11
A hemispherical surface of radius R is placed with its cross-section perpendicular to a uniform electric field E as shown in figure. Flux linked with its curved surface is
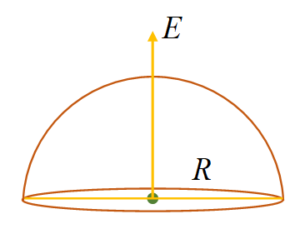
(a) zero
(b) 2\pi {{R}^{2}}E
(c) \pi {{R}^{2}}E
(d) \frac{E}{{2{{\varepsilon }_{o}}}}
Ans. (c)
Q.12
A hollow conducting uniformly charged sphere of radius R does not produce an electric field at any
(a) Interior point
(b) Exterior point
(c) Point beyond 2R metre
(d) Point beyond 10R metre
Ans. (a)
Q.13
A positive point charge, which is free to move, is placed inside a hollow conducting sphere, placed away from it centre. The conducting sphere is uniformly charged with negative charge. The positive charge will
(1) Move towards the centre
(2) Move towards the nearer wall of the conductor
(3) Remain stationary
(4) Oscillate between the centre and the nearer wall
Ans. (3)
Q.14
How does the electric field strength vary when one move from the center to surface of a uniformly charged spherical cloud ?
(1) Decreases inversely as the square of the distance from the surface.
(2) Decreases directly as the square of the distance from the surface
(3) Increase directly as the square of the distance from the centre
(4) Increases directly as the distance from the centre.
Ans. (4)
Q.15
Gauss’s law helps in
(1) Determination of electric force between point charges
(2) Situations where Coulomb’s law fails
(3) Determination of electric field due to symmetric charge distributions
(4) Determining electric potential due to symmetric charge distributions.
Ans. (3)
Q.16
Which one of the following graphs, figures shows the variation of electric field strength E with distance d from the centre of the hollow conducting sphere ?

Ans (d)
Q.17
If an insulated non-conducting sphere of radius R has charge density \rho. The electric field at a distance r from the centre of sphere (r<R) will be
(a) \frac{{\rho R}}{{3{{\varepsilon }_{0}}}}
(b) \frac{{\rho r}}{{{{\varepsilon }_{0}}}}
(c) \frac{{\rho r}}{{3{{\varepsilon }_{0}}}}
(d) \frac{{3\rho R}}{{{{\varepsilon }_{0}}}}
Ans (c)
Q.18
Shown in the figure is a distribution of charges. The flux of electric field due to these charges through the surface is
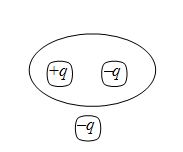
(a) \frac {3q}{{\varepsilon}_{o}}
(d) \frac {2q}{{\varepsilon}_{o}}
(c) \frac {q}{{\varepsilon}_{o}}
(d) Zero
Ans (d)
Q.19
The inward and outward electric flux for a closed surface in units of N-m2/coulomb are respectively 8 × 103 and 4 × 103. Then the total charge inside the surface is
(a) 4 × 103 coulomb
(b) -4\times {{10}^{3}} coulomb
(c) -\frac{{4\times {{{10}}^{3}}}}{{{{\varepsilon }_{0}}}} coulomb
(d) -4\times {{10}^{3}}\times{{\varepsilon}_{o}} coulomb
Ans (d)
Subjective Assignment
Q.1
A hemisphere of radius 20cm is kept in a uniform electric field of 200N/C. If its circular base is perpendicular to the electric field find the electric flux passing through the hemisphere.
Ans: 25.12 N{{m}^{2}}/C
Q.2
Two charges of 10 \mu C each are kept at a distance of 10cm and 30 cm from the center of a hollow sphere of radius 20cm. Find the electric flux passing through the spherical surface.
Ans: 1.12 \times {{10}^{6}} N{{m}^{2}}/C
Q.3
A charge of 20 \mu C is kept at a distance of 10cm above the center of a square plane of side 20cm lying horizontally. Find the electric flux passing through the plane.
Ans: 3.76 \times {{10}^{5}} N{{m}^{2}}/C
Q.4
Consider a uniform electric field E= 3 \times {{10}^{3}}{ }\hat i { }N/C .
(a) What is the flux of this field through a square of 10 cm side whose plane is parallel to the yz plane?
(b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
(c) What is the net flux of the uniform electric field through a cube of side 20cm oriented so that its faces are parallel to the coordinate planes?
Ans: (a) 300 N{{m}^{2}}/C, (b)150 N{{m}^{2}}/C, (c) zero
Q.5
A line of charge of infinite length and linear charge density 10 \mu C/m is kept coaxial with a cylinder of radius 5cm and length 50cm. Find the electric flux passing through the cylinder.
Ans: 5.64 \times {{10}^{5}} N{{m}^{2}}/C
Q.6
Three charges of 10\mu C , -40\mu C and 50\mu C are enclosed by a surface. Find the net flux passing through the surface.
Ans: 2.25 \times {{10}^{6}} N{{m}^{2}}/C
Q.7
The electric field in a region is given by \overrightarrow{E}= \frac {3}{4}{{E}_{o}} \hat i +\frac {4}{3}{{E}_{o}} \hat j with {{E}_{o}}= 6000N/C. Find the flux passing through a rectangular surface of area 4{{m}^{2}} parallel to the x-z plane.
Ans: 32 \times {{10}^{3}} N{{m}^{2}}/C
Q.8
A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
Ans: \frac {Q}{2{{\varepsilon}_{o}}}
Q.9
Show that there can be no net charge in a region in which the electric field is uniform at all points.
Ans: (Hint: The net flux passing through the region is zero in a uniform electric field and use Gauss’s theorem)
Q.10
The electric field in a region is given by \overrightarrow{E}= {{E}_{o}}(2+x) \hat i N/C . Find the charge contained inside a cubical volume bounded by the surfaces x = 0, x = 1m, y = 0, y = 1m, z = 0 and z = 1m. Take {{E}_{o}}=5000 N/Cm
Ans: -4.4 \times {{10}^{-8}} C
Q.11
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and the Gauss’s law, find the flux of the electric field due to this charge through the hemispherical surface and the circular base .
Ans: \frac {Q}{2{{\varepsilon}_{o}}}, zero
Q.12
A spherical volume contains a uniformly distributed charge of density 2\times {{10}^{4}} C/{{m}^{3}}. Find the electric field at a point inside the volume at a distance 4.0 cm from the centre.
Ans: 3 \times {{10}^{13}} N{{m}^{2}}/C
Q.13
Two charges of magnitudes–2Q and +Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ and ‘5a’ respectively with its centre at the origin?
Ans: \frac {-2Q}{{{\varepsilon}_{o}}}, \frac {-Q}{{{\varepsilon}_{o}}}
Q.14
Define electric flux. Write its S.I.unit. A charge q is enclosed by a spherical surface of radius R. If the radius is reduced to half, how would the electric flux through the surface change ?
Ans: S.I. unit : N{{m}^{2}}/C, remains same
Q.15
A positive point charge (+q) is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines originating from the point on to the surface of the plate. Derive the expression for the electric field at the surface of a charged conductor.
Ans: Try yourself
Q.16
Use Gauss Theorem to find the electric field in the following cases
(1) Outside and inside a solid nonconducting cylinder with uniform volume charge density \rho
(2) Outside and inside a solid conducting spherical shell with uniform surface charge density \sigma
(3) Outside and inside a thick conductor. Write the S.I. units of the charge density used for finding this electric field.
Ans: Refer the video lectures for derivation of elctric fields
Q.17
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17\times{{10}^{-22}} C{{m}^{-2}} .Find the acceleration of two protons :
(a) one released in the outer region of the plates,
(b) second released in the inner region of the plates.
Take mass of proton = 1.6\times{{10}^{-27}}kg
Ans: zero , 0.0187 m{{s}^{-2}}
Q.18
A dipole has two equal and opposite charges \pm1\mu C each situated at (0,0) and (1,0).Two spheres with equation {{x}^{2}}+{{y}^{2}}+{{z}^{2}}=4 and {{(x-1)}^{2}}+{{y}^{2}}+{{z}^{2}}=0.04 are present in that region. Find the flux passing through them.
Ans: zero, 1.1 \times {{10}^{5}} N{{m}^{2}}/C
