Video Lecture
Theory For Making Notes
Collision
Collision may be considered as a phenomenon of observation of mutual action and reaction force of great magnitude between particles for a very short interval of time. Collision is a brief event between objects that interact each other through a force which may be a contact force or field force. The interaction between two or more objects is called a collision if there exists three identifiable stages to this interaction: before, during and after. In the before and after stage the interaction forces are zero or approaches zero asymptotically. Between these two states the interaction forces are large and often the dominating forces governing the object’s motion. The magnitude of the interacting force is often unknown. Therefore, the conservation of momentum statement is useful for relating the initial velocities before the interaction to the final velocities after the interaction without requiring a detailed knowledge of the interaction forces.
Types of Collision
(i)
Elastic collision
( Linear Momentum and kinetic energy both are conserved)
(ii)
Inelastic collision
(Linear Momentum is conserved but kinetic energy is not conserved)
(iii)
Perfectly Inelastic collision
( Linear Momentum is conserved and there is a maximum loss of kinetic energy)
So collisions may be either elastic or inelastic. Linear momentum is conserved in both cases. A perfectly elastic collision is defined as one in which the total kinetic energy of the particles is also conserved hence the equation of kinetic energy conservation may be written as follows
\frac{1}{2}{{m}_{1}}u_{1}^{2}+\frac{1}{2}{{m}_{2}}u_{2}^{2}=\frac{1}{2}{{m}_{1}}v_{1}^{2}+\frac{1}{2}{{m}_{2}}v_{2}^{2}
In an inelastic collision, the total kinetic energy of the particle changes. Some of the kinetic energy is stored as potential energy associated with a change in internal structure or state, and is not immediately recovered. Some of the energy may be used to raise the system (e.g. an atom) to a state with higher energy. Or, it may be converted into thermal energy of vibrating atoms and molecules or into light, sound or some other from of energy.In a completely inelastic collision, the two bodies couple or stick together.
Coefficient of Restitution
It is defined as the ratio of velocity of separation to the velocity of approach of the two colliding bodies
According to Newton’s experimental law on collisions of two bodies the relative velocity of any one of the colliding bodies relative to the other body after impact is proportional to the relative velocity of the same body before impact but opposite in direction. The constant of proportionality is called the ‘coefficient of restitution’ and it is generally denoted by ‘e’. Thus
v12(after impact) = –e × u12 (before impact) where v12 and u12 stands for the final and initial relative velocity of 1 with respect to 2.
So Coefficient of Restitutione = \frac{{\text{velocity}\,\,\text{of}\,\text{separation}}}{{velocity\,of\,appraoch}}=\left| {\frac{{{{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}}}}{{{{{\vec{u}}}_{1}}-{{{\vec{u}}}_{2}}}}} \right|
Generally e is less than 1. When e = 1, collision is said to be ‘perfectly elastic’. It is to be remembered that when collision takes place between a particle and a smooth heavy wall, only the perpendicular components of velocities before and after impact are subject to Newton’s law and not the ones parallel to the wall. The components of velocities before and after impact parallel to the wall remain unaltered.
Impact Parameter: Head-on Collision
Suppose that a spherical ball of radius R approaches another spherical ball at rest and of radius r. Draw a line through the center of the ball at rest parallel to the direction of motion of the other ball. Then the perpendicular distance between these two lines is called the impact parameter of collision.
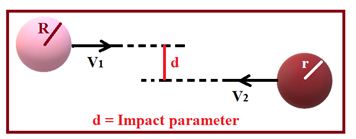
Depending on impact parameter there are two types of collisions
Head-on elastic collision [one dimensional elastic collision]
Consider two bodies A and B of masses m1 and m2 respectively moving along the same straight line in the same direction. Let u1 and u2 be their respective magnitudes of velocities such that u1> u2
The two bodies will collide after some time.
Let v1 and v2 be the magnitude of velocities of A and B respectively after the collision.

Applying the law of conservation of momentum,
total momentum before collision = total momentum after collision
{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} (in magnitude)
or {{m}_{1}}({{u}_{1}}-{{v}_{1}})={{m}_{2}}({{v}_{2}}-{{u}_{2}}) …(i)
Since the collision is elastic therefore kinetic energy will be conserved.
Kinetic energy before collision = Kinetic energy after collision
\frac{1}{2}{{m}_{1}}{{u}_{1}}_{{}}^{2}+\frac{1}{2}{{m}_{2}}{{u}_{2}}_{{}}^{2}=\frac{1}{2}{{m}_{1}}{{v}_{1}}_{{}}^{2}+\frac{1}{2}{{m}_{2}}{{v}_{2}}_{{}}^{2}
or {{m}_{1}}({{u}_{1}}+{{v}_{1}})\,({{u}_{1}}-{{v}_{1}})\,={{m}_{2}}({{v}_{2}}+{{u}_{2}})\,({{v}_{2}}-{{u}_{2}}) …(ii)
Dividing (ii) by (i), we get
{{u}_{1}}+{{v}_{1}}={{v}_{2}}+{{u}_{2}}
or {{u}_{1}}-{{u}_{2}}={{v}_{2}}-{{v}_{1}} …(iii)
\displaystyle ({{u}_{1}}-{{u}_{2}}) is the magnitude of the relative velocity of A with respect to B i.e. relative velocity before the collision. Whereas ({{v}_{2}}-{{v}_{1}}) is the magnitude of relative velocity of B with respect to A after the collision. It may be noted that the direction of relative velocity is reversed after the collision.
From equation (iii), {{v}_{2}}={{u}_{1}}-{{u}_{2}}+{{v}_{1}} , let’s put it in equation (i)
From equation (i),
{{m}_{1}}({{u}_{1}}-{{v}_{1}})={{m}_{2}}({{u}_{1}}-{{u}_{2}}+{{v}_{1}}-{{u}_{2}})
on solving for v1 we get \displaystyle {{v}_{1}}=\frac{{{{m}_{1}}-{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{1}}+\frac{{2{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{2}} …(iv)
Again, from equation (iii),
{{v}_{1}}={{v}_{2}}-{{u}_{1}}+{{u}_{2}}
Substituting this value in equation (i) and simplifying, we get
{{v}_{2}}=\frac{{{{m}_{2}}-{{m}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{2}}+\frac{{2{{m}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{1}} …(v)
Special Cases Of Elastic One Dimensional Collision
(i)
When two bodies of equal masses collide elastically head-on, their velocity will interchange as shown in the figure given below
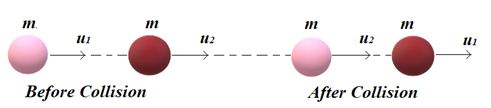
(ii)
When a very light body of very small mass collide elastically head-on with a stationary heavy body of very large mass then the lighter body rebound with the same speed whereas the heavy body remains stationary.
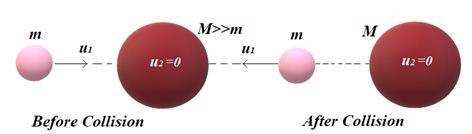
(iii)
When a very heavy body of very large mass collide elastically head-on with a stationary light body of very small mass then the heavy body continues to move with the same initial speed the lighter body moves with a speed double that of the initial velocity of the heavier body.
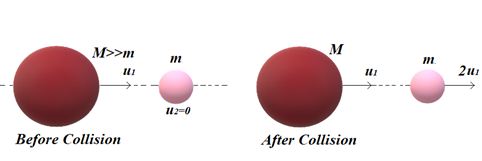
Perfectly Inelastic Collision
In this type of collision the two bodies acquire equal velocity along the line of impact after the collision . One of the example of this type of collision is when the two bodies stick together after the collision. Consider two masses m1 and m2 moving along the same line with speed u1 and u2 in the same direction as shown in the figure.
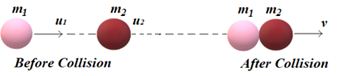
By the law of conservation of momentum
{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}=({{m}_{1}}+{{m}_{2}})v
v=\frac{{{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}
In this case maximum loss of kinetic energy takes place . Let’s calculate the loss in kinetic energy .
\Delta K=\left( {\frac{1}{2}{{m}_{1}}u_{1}^{2}+\frac{1}{2}{{m}_{2}}u_{2}^{2}} \right)-\frac{1}{2}({{m}_{1}}+{{m}_{2}}){{v}^{2}}
By substituting the value of v we get \Delta K=\frac{1}{2}\left( {\frac{{{{m}_{1}}{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}} \right)\,{{({{u}_{1}}-{{u}_{2}})}^{2}}
Head on Inelastic Collision

Let two bodies of mass m1and m2 collide inelastically and coefficient of restitution is e.
Where e=\frac{{{{v}_{2}}-{{v}_{1}}}}{{{{u}_{1}}-{{u}_{2}}}}=\frac{{\text{Relative velocity of separation}}}{{\text{Relative velocity of approach}}}
{{v}_{2}}-{{v}_{1}}=e({{u}_{1}}-{{u}_{2}})
\displaystyle {{v}_{2}}-{{v}_{1}}=e({{u}_{1}}-{{u}_{2}}) …(i)
From the law of conservation of linear momentum
{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} …(ii)
By solving (i) and (ii) we get
{{v}_{1}}=\left( {\frac{{{{m}_{1}}-e{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}} \right)\,{{u}_{1}}+\left( {\frac{{(1+e)\,{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}} \right)\,{{u}_{2}}
Similarly {{v}_{2}}=\left[ {\frac{{(1+e)\,{{m}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}} \right]\,{{u}_{1}}+\left( {\frac{{{{m}_{2}}-e\,{{m}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}} \right)\,{{u}_{2}}
Ratio of velocities after inelastic collision : A sphere of mass m moving with velocity u hits inelastically with another stationary sphere of same mass.
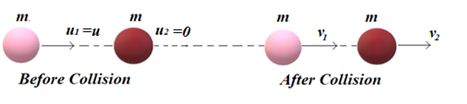
e=\frac{{{{v}_{2}}-{{v}_{1}}}}{{{{u}_{1}}-{{u}_{2}}}}=\frac{{{{v}_{2}}-{{v}_{1}}}}{{u-0}}
{{v}_{2}}-{{v}_{1}}=eu …(i)
By conservation of momentum :
Momentum before collision = Momentum after collision
mu=m{{v}_{1}}+m{{v}_{2}}
Þ {{v}_{1}}+{{v}_{2}}=u …(ii)
Solving equation (i) and (ii) we get {{v}_{1}}=\frac{u}{2}(1-e)
and {{v}_{2}}=\frac{u}{2}(1+e)
\ \frac{{{{v}_{1}}}}{{{{v}_{2}}}}=\frac{{1-e}}{{1+e}}
Calculation of Loss in kinetic energy
Loss in K.E. (ΔK) = Total initial kinetic energy – Total final kinetic energy
= \left( {\frac{1}{2}{{m}_{1}}u_{1}^{2}+\frac{1}{2}{{m}_{2}}u_{2}^{2}} \right)-\left( {\frac{1}{2}{{m}_{1}}v_{1}^{2}+\frac{1}{2}{{m}_{2}}v_{2}^{2}} \right)
Substituting the value of {{v}_{1}} and {{v}_{2}} from the above expressions
Loss (ΔK) = \frac{1}{2}\left( {\frac{{{{m}_{1}}{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}} \right)\,(1-{{e}^{2}})\,{{({{u}_{1}}-{{u}_{2}})}^{2}}
By substituting e = 1 we get ΔK = 0 i.e. for perfectly elastic collision, loss of kinetic energy will be zero or kinetic energy remains same before and after the collision.
Elastic collision in two dimensions (Oblique collision)
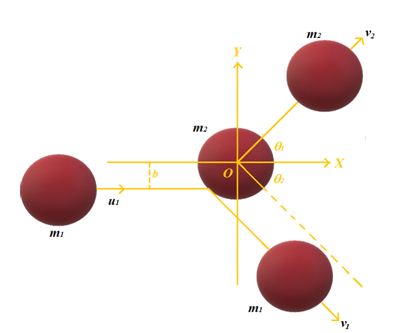
Consider two masses m1 and m2 collide with a impact parameter b. Initially m1 is moving with speed u1 whereas the mass m2 is at rest .
Applying the law of conservation of momentum to the x-component of motion, we get
{{m}_{1}}{{u}_{1}}={{m}_{1}}{{v}_{1}}\cos {{\theta }_{1}}+{{m}_{2}}{{v}_{2}}\cos {{\theta }_{2}} …(i)
For y-component of motion,
{{m}_{1}}{{v}_{1}}\sin {{\theta }_{1}}-{{m}_{2}}{{v}_{2}}\sin {{\theta }_{2}}=0 …(ii)
The collision is elastic. So kinetic energy will be conserved.
\frac{1}{2}{{m}_{1}}{{u}_{1}}_{{}}^{2}=\frac{1}{2}{{m}_{1}}{{v}_{1}}_{{}}^{2}+\frac{1}{2}{{m}_{2}}{{v}_{2}}_{{}}^{2}
or {{m}_{1}}{{u}_{1}}_{{}}^{2}={{m}_{1}}{{v}_{1}}_{{}}^{2}+{{m}_{2}}{{v}_{2}}_{{}}^{2} …(iii)
The equations (i), (ii) and (iii) can be used to solve this problem.
Special case : If {{m}_{1}}={{m}_{2}} and {{u}_{2}}=0 substituting these values in equation (i), (ii) and (iii) we get
{{u}_{1}}={{v}_{1}}\cos {{\theta }_{1}}+{{v}_{2}}\cos {{\theta }_{2}} …(iv)
0={{v}_{1}}\sin {{\theta }_{1}}-{{v}_{2}}\sin {{\theta }_{2}} …(v)
And u_{1}^{2}=v_{1}^{2}+v_{2}^{2} …(vi)
Squaring (iv) and (v) and adding we get
u_{1}^{2}=v_{1}^{2}+v_{2}^{2}+2{{v}_{1}}{{v}_{2}}\cos ({{\theta }_{1}}+{{\theta }_{2}}) …(vii)
Using (vi) and (vii) we get \displaystyle \cos ({{\theta }_{1}}+{{\theta }_{2}})=0
{{\theta }_{1}}+{{\theta }_{2}}=\pi /2
i.e. after perfectly elastic oblique collision of two bodies of equal masses (if the second body is at rest), the scattering angle {{\theta }_{1}}+{{\theta }_{2}} would be {{90}^{o}}.
Illustration
A ball moving with a speed of 9m/s strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of 30° with the original line of motion. Find the speeds of the two balls after collisions.
Solution:
Here, {{m}_{1}}={{m}_{2}}=m, {{u}_{1}}=9\,\text{m/s},{{u}_{2}}=0
{{\theta }_{1}}={{\theta }_{2}}=30{}^\circ ,{{v}_{1}}=?{{v}_{2}}=?
Applying principle of conservation of linear momentum
(i)
along the direction of motion (X-axis) {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}\cos {{\theta }_{1}}+{{m}_{2}}{{v}_{2}}\cos {{\theta }_{2}}
m\times 9+0=m{{v}_{1}}\cos 30{}^\circ +m{{v}_{2}}\cos 30{}^\circ
or, 9={{v}_{1}}\sqrt{3}/2+{{v}_{2}}\sqrt{3}/2=\frac{{({{v}_{1}}+{{v}_{2}})\sqrt{3}}}{2}
{{v}_{1}}+{{v}_{2}}=\frac{{18}}{{\sqrt{3}}} …(i)
(ii)
along a direction perpendicular to the direction of motion (Y-axis)
0+0={{m}_{1}}{{v}_{1}}\sin {{\theta }_{1}}-{{m}_{2}}{{v}_{2}}\sin {{\theta }_{2}}
{{m}_{1}}{{v}_{1}}\sin {{\theta }_{1}}={{m}_{2}}{{v}_{2}}\sin {{\theta }_{2}}
m{{v}_{1}}\sin 30{}^\circ =m{{v}_{2}}\sin 30{}^\circ
{{v}_{1}}={{v}_{2}}
Put in (i) 2{{v}_{1}}=\frac{{18}}{{\sqrt{3}}}
{{v}_{1}}=\frac{9}{{\sqrt{3}}}=\frac{{9\sqrt{3}}}{{\sqrt{3}\sqrt{3}}}=3\sqrt{3}\ \text{m/s}
Hence the two balls move with the same velocity \displaystyle =3\sqrt{3}\ \text{m/s} after collision. Ans.
Illustration
Two ball bearings of mass m each moving in opposite directions with equal speed v collides head on with each other. Predict the out come of the collision, assuming it to be perfectly elastic.
Solution:
Here, {{m}_{1}}={{m}_{2}}=m, {{u}_{1}}=v,\ {{u}_{2}}=-v
Velocities of the two balls after perfectly elastic collision between them are
v=\frac{{({{m}_{1}}-{{m}_{2}}){{u}_{1}}+2{{m}_{2}}{{u}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}
{{v}_{1}}=\frac{{0+2m(-v)}}{{m+m}}=-v
{{v}_{2}}=\frac{{({{m}_{2}}-{{m}_{1}}){{u}_{2}}+2{{m}_{1}}{{u}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}} =\frac{{0+2mv}}{{2m}}=v
After collision, the two ball bearings will move with same speeds, but their directions of motion will be reversed.
Illustration
A railway carriage of mass 10000 kg moving with a speed of 15ms–1 strikes a stationary carriage of the same mass. After the collision, the carriages get coupled and move together. What is their common speed after collision?
Solution:
Here, {{m}_{1}}=10000kg, {{v}_{1}}=15\text{m}{{\text{s}}^{{-1}}} , {{m}_{2}}=10000kg,\ {{v}_{2}}=0,\ v=?
As the collision is perfectly inelastic, therefore,
({{m}_{1}}+{{m}_{2}})v={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}
(10000+10000)v=10000\times 15+0
v=\frac{{10000\times 15}}{{20000}}=7.5\text{m}{{\text{s}}^{{-1}}}.
Illustration
A ball of 0.1 kg makes an elastic head on collision with a ball of unknown mass initially at rest. If the 0.1 kg ball rebounds at one third of its original speed, what is the mass of the other ball?
Solution:
Here, {{m}_{1}}=0.1\text{kg}\ {{m}_{2}}=?
{{u}_{2}}=0 Let {{u}_{1}}=u;
As {{v}_{1}}=\frac{{({{m}_{1}}-{{m}_{2}}){{u}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}+\frac{{2{{m}_{2}}{{u}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}
{{v}_{1}}=-\frac{u}{3}
-\frac{u}{3}=\frac{{(0.1-{{m}_{2}})u}}{{0.1+{{m}_{2}}}}
or -\frac{1}{3}=\frac{{0.1-{{m}_{2}}}}{{0.1+{{m}_{2}}}}
or -0.3+3{{m}_{2}}=0.1+{{m}_{2}}
2{{m}_{2}}=0.1+0.3=0.4
{{m}_{2}}=\frac{{0.4}}{2}\text{kg}.=0.2\text{kg}\text{.}
Illustration
A ball of mass m approaches a wall of mass M (>>m) with speed 4 m/s along the normal to the wall. The speed of wall is 1 m/s towards the ball. The speed of the ball after an elastic collision with the wall is
(a) 5 m/s away from the wall
(b) 9 m/s away from the wall
(c) 3 m/s away from the wall
(d) 6 m/s away from the wall
Solution
Let v be the velocity of ball after collision
Collision is elastic.
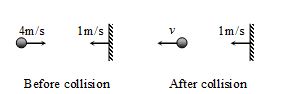
e = 1
or,
relative velocity of separation = relative velocity of approach
v-1=4+1
or
v = 6 m/s (away from the wall)
(d)
Illustration
A ball A of mass m moving with velocity u, collides head on with another ball B of the same mass at rest. If the co-efficient of restitution between balls is e, the ratio of the final and initial velocities of ball A will be
(a) \frac{{1+e}}{{1-e}}
(b) \frac{{1+e}}{2}
(c) 1 – e
(d) \frac{{1-e}}{2}
Solution
mu=m{{v}_{1}}+m{{v}_{2}}
u={{v}_{1}}+{{v}_{2}} …(1)
e = \frac{{{{v}_{2}}-{{v}_{1}}}}{u}
v2 = eu + v1 …(2)
from equation (1) and (2)
u = v1 + eu + v1
\frac{{{{v}_{1}}}}{u}=\frac{{1-e}}{2}
(d)
Practice Questions (Level-1)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-2)
1.
A ball is allowed to fall from a height of 10m. If there is 40% loss of energy due to impact, then after one impact the ball will bounce upto
(a) 10 m
(b) 8 m
(c) 4 m
(d) 6 m
Ans (d)
2.
A body of mass m having an initial velocity v, makes head on elastic collision with a stationary body of mass M. After the collision, the body of mass m comes to rest and only the body having mass M moves. This will happen only when
(a) m>>M
(b) m<<M
(c) m = M
(d) m=\frac{1}{2}M
Ans (c)
3.
A ball hits the floor and rebounds after collision. Which of the following is correct?
(a) The total momentum of the ball and the earth is conserved
(b) The total energy of the ball and the earth is conserved
(c) The mechanical energy of the ball remains the same in the collision
(d) The momentum of the ball just after collision is zero
Ans (a)
4.
If a particle of mass m1 approaches mass m2 , initially at rest, with speed v1, then the speed of the centre of mass of the system is \frac{{{{m}_{1}}{{v}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}} before collision takes place. If the collision is perfectly elastic, then the speed of the centre of mass of the system after the collision is
(a) \frac{{{{m}_{2}}{{v}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}
(b) \frac{{{{m}_{1}}{{v}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}
(c) \frac{{{{m}_{2}}-{{m}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}{{v}_{1}}
(d) zero
Ans (b)
5.
Two perfectly elastic particles P and Q of equal mass are travelling along the line joining them with velocities 15 m s–1 and 10 ms–1 respectively. After collision, their velocities respectively (in ms–1) will be
(a) 0, 25
(b) 5, 20
(c) 10, 15
(d) 20, 5
Ans (c)
6.
A moving body with a mass m1 strikes a stationary body of mass m2. The masses m1 and m2 should be in the ratio m1/m2 so as to decrease the velocity of the first body 1.5 times assuming a perfectly elastic impact. Then the ratio m1/m2 is
(a) 5
(b) 1/5
(c) 1/25
(d) 25
Ans (a)
7.
A glass marble dropped from a certain height above the horizontal surface reaches the surface in time t and then continues to bounce up and down. The time in which the marble finally comes to rest is
(a) et
(b) e2t
(c) t\,\left[ {\frac{{1+e}}{{1-e}}} \right]
(d) t\,\left[ {\frac{{1-e}}{{1+e}}} \right]
Ans (c)
8.
A nucleus ruptures into two parts which have their velocity ratio equal to 2 : 1. The ratio of their respective nuclear size (nuclear radii) is
(a) 1 : 2
(b) 1:\sqrt{2}
(c) 1 : 21/3
(d) 1 : 8
Ans (c)
9.
A ball is dropped from a height h on the ground. If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
(a) h{{e}^{{2n}}}
(b) h{{e}^{n}}
(c) \frac{{{{e}^{{2n}}}}}{h}
(d) \frac{h}{{{{e}^{{2n}}}}}
Ans (a)
10.
A technician is experimenting to construct laboratory model of a rifle. He observes that if the length of the barrel of the rifle is cut by 1cm, the velocity of the bullet is reduced from \sqrt{5}\ \text{m}{{\text{s}}^{{-1}}} to 2 ms–1. If the bullet weighs 50g, then the force acting on the bullet is
(a) 1 N
(b) 1.5 N
(c) 2.5 N
(d) 3.5 N
Ans (c)
11.
The quantities remaining constant in a elastic collision are
(a) momentum, kinetic energy and temperature
(b) momentum and kinetic energy but not temperature
(c) momentum and temperature but not kinetic energy
(d) momentum, but neither kinetic energy nor temperature
Ans (a)
12.
What percentage of kinetic energy of a moving particle is transferred to a stationary particle when it suffers one-dimensional elastic collision with the stationary particle? [Given: mass of stationary particle = mass of moving particle]
(a) 25 %
(b) 50 %
(c) 75 %
(d) 100 %
Ans (d)
13.
A heavy steel ball of mass greater than 1 kg moving with a speed of 2 ms–1, collides head-on with a stationary ping-pong ball of mass less than 0.1g. The collision is elastic. After the collision, the ping-pong ball moves approximately with speed
(a) 2 ms–1
(b) 4 ms–1
(c) 2 × 104ms–1
(d) 2 × 103ms–1
Ans (b)
14.
A sphere of mass m moving horizontally with velocity v0 collides against a pendulum bob of mass m. If the two masses stick together after the collision, then the maximum height attained is
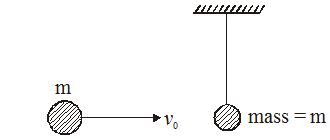
(a) \frac{{v_{0}^{2}}}{{2g}}
(b) \frac{{v_{0}^{2}}}{{4g}}
(c) \frac{{v_{0}^{2}}}{{6g}}
(d) \frac{{v_{0}^{2}}}{{8g}}
Ans (c)
15.
A metal ball hits a wall and does not rebound whereas a rubber ball of the same mass on hitting the wall with the same velocity rebounds back. It can be concluded that
(a) metal ball suffers greater change in momentum
(b) rubber ball suffers greater change in momentum
(c) the initial momentum of metal ball is greater than initial momentum of rubber ball
(d) both suffer same change in momentum
Ans (b)
16.
The velocities of two bodies having masses 5 kg and 10 kg are 4 ms–1 and 2 ms–1 respectively along x and y axes. They collide and stick together. The compound body moves with velocity v at angle q with x-axis. The value of q is
(a) 30°
(b) 45°
(c) 60°
(d) –75°
Ans (b)
17.
A bullet moving with a velocity of 800 ms–1 passes through two plates of widths d1 and d2. In passing through each of them, it loses a velocity of 200 ms–1. If both the plates offer same resistance to the motion of bullet, then the radio d1/d2 is
(a) \frac{7}{5}
(b) \frac{5}{7}
(c) \frac{4}{3}
(d) \frac{3}{4}
Ans (a)
18.
A bullet of mass 50 g moving with a velocity of 400 ms–1 strikes a wall and goes out from the other side with a velocity of 100ms–1. Calculate work done in passing through the wall.
(a) 3.75 × 103J
(b) 3.00 × 103J
(c) 2.50 × 103J
(d) 3.75 × 10-3J
Ans (a)
19.
A block of mass m moving at a speed v compresses a spring through a distance x before its speed is halved. Find the spring constant of the spring.
(a) -3mv2/-4x2
(b) 2mv2/5x2
(c) 6mv2/8x2
(d) 3mv2/4x2
Ans(d)
20.
A ball is dropped vertically from rest at a height of 12 m. After striking the ground, it bounces back to a height of 9m. What percentage of K.E. does it lose on striking the ground?
(a) 20%
(b) 25%
(c) 35%
(d) 50%
Ans (b)
21.
A body of mass 2.0 kg makes an elastic collision with another body at rest and continues to move in the original direction with a speed equal to half its original speed. Find the mass of the second body.
(a) 0.20 kg
(b)1.00 kg
(c) 0.67 kg
(d) 0.50 kg
Ans (c)
22.
What percentage of K.E. of a moving particle is transferred to a stationary particle when it strikes the stationary particle of 4 times its mass?
(a) 64%
(b) 50%
(c) 62%
(d) 30%
Ans (a)
23.
A sphere of mass m moving with velocity u hits another stationary sphere of same mass. If e is coefficient of restitution, what is the ratio of velocities of two spheres after collision?
(a) \frac{{1+e}}{{1+e}}
(b) \frac{{1-e}}{{1-e}}
(c) \frac{{1-e}}{{1+e}}
(d) \frac{{1+e}}{{1-e}}
Ans (c)
Comprehension Based Question (24 and 25)
What percentage of K.E. of a moving particle is transferred to stationary particle, when it strikes the stationary particle of
24.
100 times its mass
(a) 2.00 %
(b) 3.92 %
(c) 2.05 %
(d)4.33 %
Ans (b)
25.
equal mass?
(a) 65%
(b) 30%
(c) 10%
(d) 100%
Ans (d)
26.
A ball of mass m hits a floor with a speed v making an angle of incidence q with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
(a) v\prime =v\sqrt{{{{{\sin }}^{-2}}\theta +{{e}^{2}}{{{\cos }}^{4}}\theta }},\ \theta \prime ={{\tan }^{{-3}}}(\tan \theta /e)
(b) v\prime =v\sqrt{{{{{\sin }}^{2}}\theta +{{e}^{2}}{{{\cos }}^{2}}\theta }},\ \theta \prime ={{\tan }^{{-1}}}(\tan \theta /e)
(c) v\prime =v\sqrt{{{{{\sin }}^{2}}\theta +{{e}^{4}}{{{\cos }}^{2}}\theta }},\ \theta \prime ={{\tan }^{{1}}}(\tan \theta /e)
(d) v\prime =v\sqrt{{{{{\sin }}^{-2}}\theta +{{e}^{-2}}{{{\cos }}^{2}}\theta }},\ \theta \prime ={{\tan }^{{-1}}}(\tan \theta /e)
Ans (b)
27.
A body falling on the ground from a height of 10m rebounds to a height of 2.5 m. Calculate the percentage loss of kinetic energy of the body during its collision with the ground
(a)20%
(b) 75%
(c) 50%
(d) 60%
Ans (b)
