Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-1)
Q.1
If a long cylindrical conductor carries a steady current parallel to its length,
(a) the electric field along the axis is zero
(b) the magnetic field along the axis is zero
(c) the magnetic field outside the conductor is zero
(d) the direction of electric field outside the conductor is perpendicular to the length of conductor .
Ans. (b)
Q.2
A vertical solenoid has 200 turns in a length of 0.40 m and carries a current of 3 A in the direction shown. The flux density in the middle in tesla (T) is about
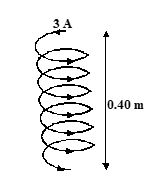
(a) 1.9 ´ 10-3 and downward
(b) 2.9 ´ 10-5 and upward
(c) 1.9 ´ 10-3 and upward
(d) 0.19 and upward
Ans :(C)
Q.3
A uniformly distributed current I flows through a cylindrical conductor of radius r. The magnetic field at a point x (< r) is
(a) \frac{{{{\mu }_{0}}I}}{{2\pi x}}
(b) \frac{{{{\mu }_{0}}I}}{{2\pi (x-r)}}
(c) \frac{{{{\mu }_{0}}Ix}}{{2\pi {{r}^{2}}}}
(d) \frac{{{{\mu }_{0}}I}}{{2\pi {{{(x-r)}}^{2}}}}
Ans. (c)
4.
A current I flows uniformly along a solid rod of radius R. Show that the B–field inside this rod, at a distance r from the axis is,
(a) B=\frac{{{{\mu }_{1}}Ir}}{{3\pi {{R}^{2}}}}
(b) B=\frac{{{{\mu }_{0}}Ir}}{{5\pi {{R}^{3}}}}
(c) B=\frac{{{{\mu }_{0}}Ir}}{{9\pi {{R}^{4}}}}
(d) B=\frac{{{{\mu }_{0}}Ir}}{{2\pi {{R}^{2}}}}
Ans (d)
Practice Questions (Level-2)
Q.1
A current I flows along the length of an infinitely long, straight thin walled pipe. Then
(a) The magnetic field at any point inside the pipe is the same but not zero
(b) The magnetic field at any point inside the pipe is zero
(c) The magnetic field is zero only on the axis
(d) The magnetic field is different at different points inside the pipe
Ans : (b)
Q.2
A long metallic cylinder of radius R has a current i flowing through it. The magnetic induction B will vary with distance from the center as shown in figure
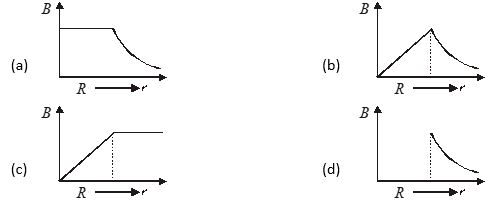
(a) a (b) b (c) c (d) d
Ans. (b)
Q.3
If a long copper rod carries a direct current, the magnetic field associated with the current will be
(a) Inside the rod only
(b) Outside the rod only
(c) Both inside and outside the rod
(d) Neither inside nor outside the rod
Ans. (c)
4.
A current I flows uniformly along a solid rod of radius R. Show that the B–field inside this rod, at a distance r from the axis is,
(a) B=\frac{{{{\mu }_{1}}Ir}}{{3\pi {{R}^{2}}}}
(b) B=\frac{{{{\mu }_{0}}Ir}}{{5\pi {{R}^{3}}}}
(c) B=\frac{{{{\mu }_{0}}Ir}}{{9\pi {{R}^{4}}}}
(d) B=\frac{{{{\mu }_{0}}Ir}}{{2\pi {{R}^{2}}}}
Ans (d)