Video Lecture
Theory For Making Notes
Thomson's Atomic Model
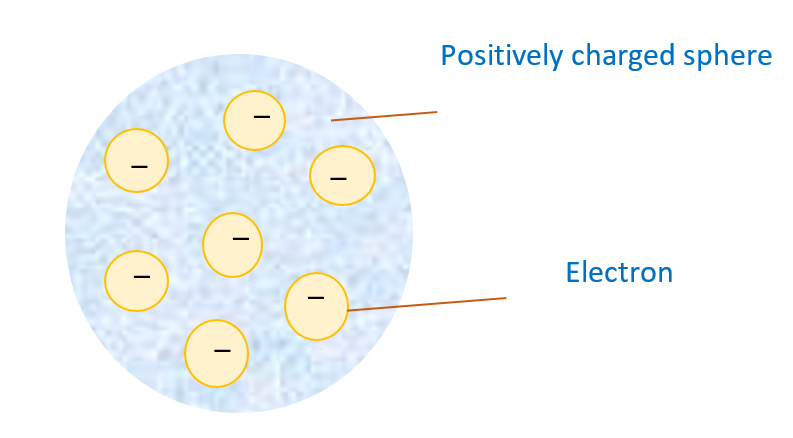
J.J. Thomson gave the first idea regarding structure of atom. According to his model an atom is a solid sphere in which entire positive charge is uniformly distributed and the negative charge (i.e. electron) are embedded like seeds in watermelon
This model explained successfully the phenomenon of thermionic emission, photoelectric emission and ionization. The model fail to explain the scattering of a– particles and it cannot explain the origin of spectral lines observed in the spectrum of hydrogen and other atoms.
Alpha Particle Scattering Experiment
Geiger and Marsden were the students of Rutherford who studied the scattering of a-particles by gold foil on the advice of Rutherford and made some of the revolutionary observations which helped Rutherford to propose a better model of atom than that of Thomson .
The experimental setup of the experiment is shown below.Here a beam of alpha particles is obtained by using slits made in Lead Screens.
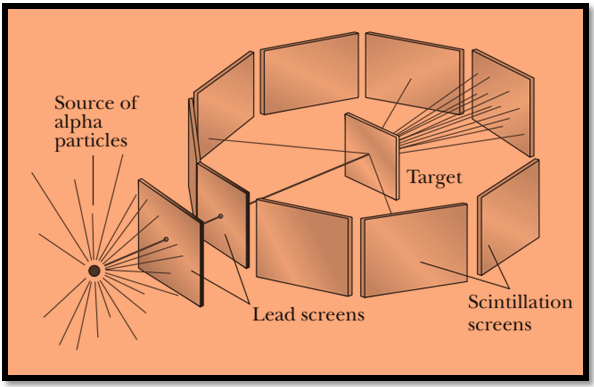
The beam is allowed to fall on a gold thin foil of thickness `t’. Screens are placed surrounding the Target (gold foil) to receive the scattered alpha particles. As an alpha particle strikes the screen , a scintillation (bright spot) is produced on the screen.
Using this setup they made the following observations:
(1) Most of the a-particles pass through the foil straight and un-deflected.
(2) Some of them are deflected through small angles.
(3) Some a-particles (1 in 1000) are deflected through an angle more than 90o.
(4) Only a few a -particles returned back after suffering a deflection of 180o.
(5) Number of scattered particles : N\propto \frac{1}{{{{{\sin }}^{4}}(\theta /2)}}
(6) If t is the thickness of the foil and N is the number of a-particles scattered in a particular direction (i.e. q = constant), it was observed that \frac{N}{t}=\text{constant} Þ \frac{{{{N}_{1}}}}{{{{N}_{2}}}}=\frac{{{{t}_{1}}}}{{{{t}_{2}}}}

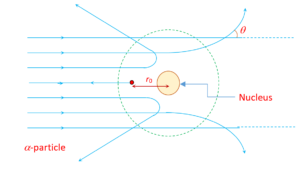
All the above observations are used to draw a picture (given below) of the scattering of alpha particles as they pass through the gold atoms of the foil (Target).
SOME IMPORTANT TERMS
Distance of closest approach (r0)
The minimum distance from the nucleus up to which the a-particle approach, is called the distance of closest approach ( \displaystyle {{r}_{0}}). The alpha-particle stops at this point and cannot go further closer of the nucleus.
Let m is the mass and v is the velocity of the alpha-particle with which it is approaching nucleus from a far off place say infinity. This distance of nearest approach, can be calculated using conservation of mechanical energy .At the distance of nearest approach all kinetic energy of alpha-particle is converted to potential energy of nucleus and electron system.

From conservation of mechanical energy
\displaystyle {{\left( {K.E.\text{ }+\text{ }P.E.} \right)}_{{initial}}}={{\left( {K.E.\text{ }+\text{ }P.E.} \right)}_{{final}}}
\Rightarrow \,\text{ }\frac{1}{2}\,m{{v}^{2}}+0=0+\,\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{\text{Ze}.2e}}{{{{r}_{0}}}}\,
hence {{r}_{0}}=\frac{{\text{Ze}.2e}}{{\text{4}\pi {{\varepsilon }_{\text{0}}}.\frac{1}{2}m{{v}^{2}}}}
or {{r}_{0}}=\frac{{\text{Z}{{\text{e}}^{2}}}}{{\pi {{\varepsilon }_{\text{0}}}.m{{v}^{2}}}}.
IMPACT PARAMETER (b)
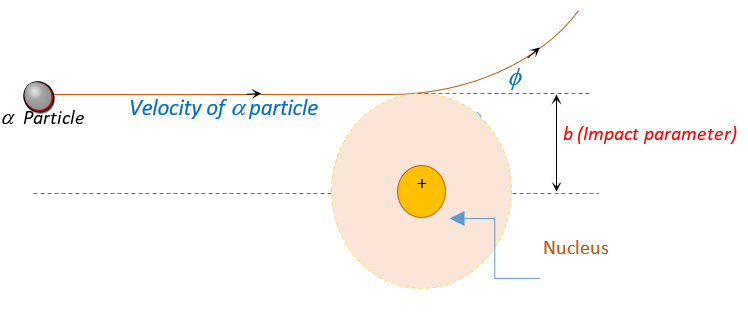
The perpendicular distance of the velocity vector ( \overrightarrow{{v\,}}) of the a-particle from the centre of the nucleus when it is far away from the nucleus is known as impact parameter.
Impact parameter is denoted by `b’ and is given as
b=\frac{{Z{{e}^{2}}\cot (\phi /2)}}{{4\pi {{\varepsilon }_{0}}\left( {\frac{1}{2}m{{v}^{2}}} \right)}}\,
hence b\propto \cot (\phi /2)
For large value of b i.e. the line of velocity of \alpha particles is far away from the nucleus ,the angle \phi will be very small hence the \alpha particles will go undeviated and for small b the \alpha-particle will suffer large scattering angle \phi.
For the case of head-on collision, impact parameter b is zero. The particle rebounds like a ball thrown against a wall, scattering through {{180}^{o}}.
SCATTERING FORMULA
In a given direction \phi the number of particles scattered is given as
The number of particles scattered at a perticular angle \phi is denoted by N(\phi ) and is given by the relation given below
N(\phi )=\frac{{{{N}_{0}}nt{{Z}^{2}}{{e}^{4}}\text{cose}{{\text{c}}^{4}}\frac{\phi}{2}}}{{16{{\pi}^{2}}\varepsilon_{0}^{2}\,{{\text{K}}^{\text{2}}}4r_{0}^{2}}}
(This is known as Rutherford scattering formula)
Where {{N}_{o}}= No. of incdent \alpha particles, e=charge of electron, n= no. of atoms per unit volume in the target, t = thickness of the target, Z= atomic number of the target, {{r}_{o}} = target to detector distance, K= kinetic energy of \alpha particles, \phi= scattering angle.
Rutherford’s Atomic Model
The correct description of the distribution of positive and negative charges within an atom was made in 1911 by a New Zealander when working at Manchester University in England. This was Ernest Rutherford, who was later made Lord Rutherford for his many scientific achievements. He entered into physics during that crucial period of its development when the phenomenon of natural radioactivity had just been discovered, and he was first to realize that radioactivity represents a spontaneous disintegration of heavy unstable atoms.
After \alpha-particles scattering experiment, following conclusions were made by Rutherford as regard as atomic structure :
(1)
Most of the mass (at least 99.95%) and all of the charge of an atom concentrated in a very small region is called atomic nucleus.
This conclusion was drawn by him seeing the large deflection of alpha particles. Such large deflections required strong forces to be acting, such as those between very smaller charged particles very close together. This would be possible, Rutherford reasoned, if all the positive charge, along with most of the atomic mass, were concentrated in a very small central region which Rutherford called the atomic nucleus.
(2)
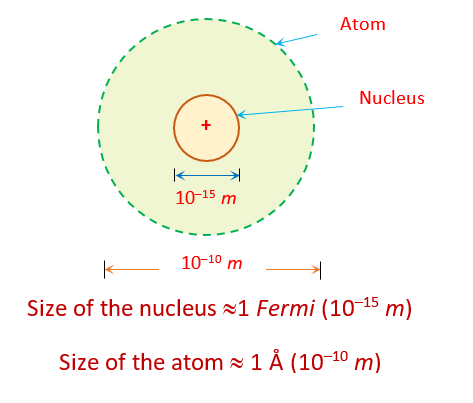
Nucleus is positively charged and it’s size is of the order of \displaystyle {{10}^{{15}}} m \displaystyle \approx 1 Fermi.
This conclusion came from the calculation of distance of nearest approach because the radius of nucleus must be less than or nearly equal to the distance of nearest approach of alpha particle.
(3)
In an atom most of the space is empty . The nucleus occupies only about \displaystyle {{10}^{{-12}}} of the total volume of the atom or less.
This conclusion came from the observation that most of the electrons goes straight without deflection.
(4)
The electrons revolve around the nucleus in the same way as the planets revolve around the sun.
The logic behind this conclusion was the question mark on stability of atoms in case of stationary electrons as suggested in Thomson Model .Because there would be a Coulomb force of attraction between the positive nucleus and the negative electrons, the two would be down together and the atom would vanish unless some provisions were made to prevent it. It was suggested that the electrons might be orbiting rapidly around the nucleus, so that the electrostatic attraction would merely provide the necessary centripetal force.
Failure of Rutherford’s Model
(1)
Stability of atom : It could not explain stability of atom because according to classical electrodynamics theory an accelerated charged particle should continuously radiate energy.
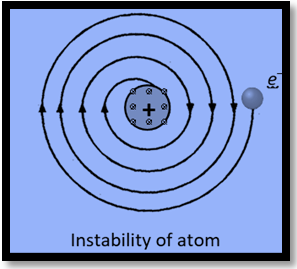
Thus an electron moving in an circular path around the nucleus should also radiate energy and thus move into smaller and smaller orbits of gradually decreasing radius and it should ultimately fall into nucleus.
(2)
According to this model the spectrum of atom must be continuous where as practically it is a line spectrum.
(3)
It did not explain the distribution of electrons outside the nucleus.
Bohr’s Theory Of Hydrogen Atom
In 1913 Bohr combined the ideas of Plank’s Quantum Theory, Einstein’s concept of photon, Rutherford’s planetary model of atom and Newtonian classical mechanics to arrive at a new model of atom which was based on some postulates. Although Bohr’s model is now completely obsolete and has been replaced by probabilistic quantum mechanical theory, we can use it to understand the energy quantization and angular momentum quantization as applied to atomic sized systems.
Three postulates of Bohr’s theory
1.
Out of several number of possible orbits, electrons can revolve only in those orbits in which the angular momentum of the electron is an integral multiple of \frac{h}{{2\pi }}.
Hence The angular momentum `L’ of electron is given as
L=mvr=\frac{{nh}}{{2\pi }} ….(ii)
Where n = 1, 2, 3 … and n is called principal quantum number. This condition is called Bohr’s quantization condition.
2.
While circling around these permitted orbits, the electrons do not emit any electromagnetic radiation. These orbits are called stationary orbits.
3.
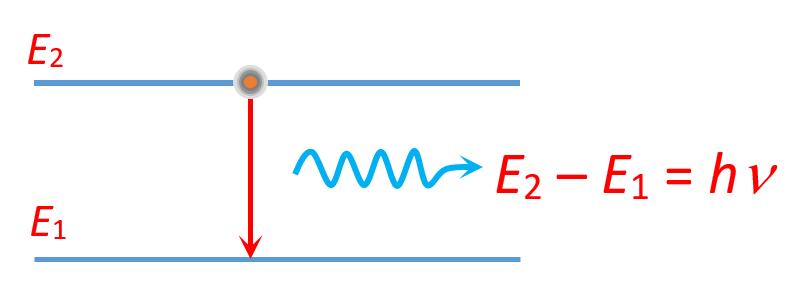
The emission or absorption of energy takes place when an electron jumps from one orbit to other.
For example if the electron jumps from an orbit of higher energy \displaystyle {{E}_{2}} to an orbit of lower energy \displaystyle {{E}_{1}} it emits a photon of radiation. The wavelength of the emitted radiation is given by the Einstein – Planck equation.
\displaystyle {{E}_{2}}-{{E}_{1}}=\frac{{hc}}{\lambda }
The electron can also absorb energy and jump from a lower energy orbit to a higher energy orbit.
IMPORTANT RELATIONS DRAWN USING BOHR’S THEORY.
(FOR DETAILED DERIVATIONS REFER THE VIDEO LECTURES)
1. Radius of \displaystyle {{n}^{{\mathbf{th}}}} allowed orbit
\displaystyle r=\frac{{{{\varepsilon }_{0}}{{h}^{2}}{{n}^{2}}}}{{\pi mZ{{e}^{2}}}}=\frac{{0.53{{n}^{2}}}}{Z}{\AA} —(i)
\Rightarrow r\propto \frac{{{{n}^{2}}}}{Z}
For example in singly ionized helium atom ( \displaystyle H{{e}^{+}}), Z = 2 and hence \displaystyle r=\frac{{0.53{{n}^{2}}}}{2}{\AA}
Similarly for doubly ionized lithium, triply ionized beryllium etc, we can find the radius of different orbits.
For hydrogen like atoms with the increase in Z, the orbits are closer to the nucleus and their relative separation also decreases in comparison to hydrogen atom.
2. Speed of electron in \displaystyle {{n}^{{\mathbf{th}}}} orbit
v=\frac{{{{e}^{2}}}}{{2{{\varepsilon }_{0}}hn}}=\frac{c}{n}\left( {\frac{{{{e}^{2}}}}{{4\pi {{\varepsilon }_{0}}\left( {\frac{h}{{2\pi }}} \right)c}}} \right)=\frac{c}{{137.n}}
In above equation, the expression between parentheses is a dimensionless constant. This is called fine structure constant and the value of fine structure constant is \frac{1}{{137}}.
3. Angular momentum of electron
As L=mvr=\frac{{nh}}{{2\pi }} and
\displaystyle v=\frac{{Z{{e}^{2}}}}{{2{{\varepsilon }_{0}}hn}},r=\frac{{0.53{{n}^{2}}}}{Z}{\AA}
we have (i) L \displaystyle \propto n, (ii) L\propto \frac{1}{v},, (iii) L\propto \sqrt{r}
As we go from inner orbit towards outer orbit, angular momentum increases. But linear momentum decreases as velocity of electron decreases.
4. Time period of revolution in \displaystyle {{n}^{th}} orbit
T=\frac{{2\pi r}}{v}.
As \displaystyle r\propto {{n}^{2}} and v\propto \frac{1}{n}, therefore, \displaystyle T\propto {{r}^{{3/2}}}, \displaystyle T\propto {{n}^{3}}.
Angular frequency, \omega \propto \frac{1}{{{{n}^{3}}}}
5. Frequency
It is the number of revolutions completed per second by the electron in a stationary orbit, around the nucleus. It is represented by f.
From, v = r \displaystyle \omega = r (2 \displaystyle \pi f)
Using, v=\frac{{Z{{e}^{2}}}}{{2{{\varepsilon }_{0}}hn}} and r=\frac{{{{\varepsilon }_{0}}{{h}^{2}}{{n}^{2}}}}{{\pi mZ{{e}^{2}}}},
we get {{f}_{n}}=\frac{v}{{2\pi r}}=\frac{{\frac{{Z{{e}^{2}}}}{{2{{\varepsilon }_{0}}hn}}}}{{2\pi \left( {\frac{{{{\varepsilon }_{0}}{{h}^{2}}{{n}^{2}}}}{{\pi mZ{{e}^{2}}}}} \right)}}
i.e., {{f}_{n}}=\frac{{{{Z}^{2}}m{{e}^{4}}}}{{4\varepsilon _{0}^{2}{{h}^{3}}{{n}^{3}}}}
Frequency, {{f}_{n}}\propto \frac{{{{Z}^{2}}}}{{{{n}^{3}}}}
For H-atom, in the first orbit, \displaystyle {{f}_{n}} = \displaystyle 6.57\text{ }\times \text{ }{{10}^{{15}}}Hz.
6. Kinetic energy of electron in \displaystyle {{n}^{{\mathbf{th}}}} orbit
{{\text{K}}_{\text{n}}}=\frac{1}{2}mV_{n}^{2}=\frac{{Z{{e}^{2}}}}{{8\pi {{\varepsilon }_{0}}r}}=\frac{{m{{e}^{4}}.\,{{Z}^{2}}}}{{8\varepsilon _{0}^{2}{{h}^{2}}{{n}^{2}}}}
7. Potential energy of electron in \displaystyle {{n}^{{\mathbf{th}}}} orbit
{{\text{U}}_{\text{n}}}=-\frac{{Z{{e}^{2}}}}{{4\pi {{\varepsilon }_{0}}{{r}_{n}}}}=\frac{{-m{{e}^{4}}.{{Z}^{2}}}}{{4\varepsilon _{0}^{2}{{h}^{2}}{{n}^{2}}}}
8. Total energy (binding energy of electron) of electron in \displaystyle {{n}^{{\mathbf{th}}}} orbit,
{{\text{E}}_{\text{n}}}={{\text{U}}_{\text{n}}}+{{\text{K}}_{\text{n}}}
{{\text{E}}_{n}}=\frac{{\text{Z}{{\text{e}}^{\text{2}}}}}{{4\pi {{\varepsilon }_{o}}r}}+\frac{{\text{Z}{{\text{e}}^{\text{2}}}}}{{8\pi {{\varepsilon }_{o}}r}}
hence {{\text{E}}_{n}}=-\frac{{Z{{e}^{2}}}}{{8\pi {{\varepsilon }_{0}}r}}
[put r=\frac{{{{\varepsilon }_{0}}{{h}^{2}}{{n}^{2}}}}{{\pi mZ{{e}^{2}}}} in the above equation ]
we get {{E}_{n}}=-\frac{{m{{e}^{4}}.\,{{Z}^{2}}}}{{8\varepsilon _{0}^{2}{{h}^{2}}{{n}^{2}}}}
\Rightarrow \text{ }{{\text{E}}_{n}}=-\frac{{m{{e}^{4}}.\,{{Z}^{2}}}}{{8\varepsilon _{0}^{2}{{h}^{2}}{{n}^{2}}}}\times \frac{{ch}}{{ch}}
Hence {{\text{E}}_{n}}=-\left[ {\frac{{m{{e}^{4}}\,}}{{8\varepsilon _{0}^{2}c{{h}^{3}}}}} \right]\times \frac{{ch{{Z}^{2}}}}{{{{n}^{2}}}}
{where \frac{{m{{e}^{4}}\,}}{{8\varepsilon _{0}^{2}c{{h}^{3}}}}= R , and is called Rydberg’s Constant. Its value is equal to \displaystyle 1.09\times {{10}^{7}}{{m}^{{-1}}}}
therefore {{E}_{n}}=-Rch\frac{{{{Z}^{2}}}}{{{{n}^{2}}}}
[Here the constant term Rch is equal to 13.6\times{e}]
So finally {{\text{E}}_{\text{n}}}=\frac{{-13.6{{Z}^{2}}}}{{{{n}^{2}}}}\text{eV}
Note that the value of Rydberg’s Constant R depends on two factors
- Whether the nucleus is stationary or not
- The location of point in space where the electrostatic potential energy is taken as zero.
The above given value of R i.e. \displaystyle 1.09\times {{10}^{7}}{{m}^{{-1}}} is for a stationary nucleus with zero potential energy at infinity.
9. Ionization potential
The negative total energy of hydrogen atom signifies that hydrogen nucleus and electron constitute a bounded system. Therefore a positive or zero energy of hydrogen atom would mean that electron is not bound to the nucleus i.e., atom is ionised. The minimum energy needed to ionise an atom is called ionisation energy,
therefore {{E}_{{ionisation}}}={{E}_{\infty }}-{{E}_{n}}=0-\left( {-13.6\frac{{{{Z}^{2}}}}{{{{n}^{2}}}}} \right)
hence {{E}_{ionisation}}=+\frac{{13.6{{Z}^{2}}}}{{{{n}^{2}}}}eV
The potential difference through which an electron should be accelerated to acquire this energy is called ionisation potential.
Hence {{V}_{{ionisation}}}=\frac{{{{E}_{{ionisation}}}}}{e}
For example the ionization energy of hydrogen atom in ground state is 13.6 eV and ionization potential is 13.6 V.
10. Binding Energy
Binding energy of a system is defined as energy liberated when its constituents are brought from infinity to form the system. For hydrogen atom binding energy is same as its ionization energy.
11. Excitation potential
The energy required to take an atom from its ground state to an excited state is called excitation energy of that excited state, and the potential through which the electron should be accelerated to acquire this is called excitation potential.
Hence {{E}_{{Excitation}}}={{E}_{{Final}}}-{{E}_{{Initial}}}
and {{V}_{{Excitation}}}=\frac{{{{E}_{{excitation}}}}}{e}
Transition Of electron and wavelength emitted
When an electron makes transition from higher energy level \displaystyle {{n}_{2}} having energy \displaystyle {{E}_{2}} to a lower energy \displaystyle {{n}_{1}} level having energy \displaystyle {{E}_{1}} then a photon of frequency \displaystyle \nu is emitted
\Delta E={{E}_{2}}-{{E}_{1}} =\frac{{-Rc\,h\,{{Z}^{2}}}}{{n_{2}^{2}}}-\left( {-\frac{{Rch\,{{Z}^{2}}}}{{n_{1}^{2}}}} \right)
=13.6{{Z}^{2}}\left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right) ,
Since \Delta E=h\nu so \nu =\frac{{\Delta E}}{h}
therefore
\nu =\frac{{\Delta E}}{h}=Rc\,{{Z}^{2}}\,\left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right)
we know that \nu =\frac{c}{\lambda }
hence \frac{c}{\lambda }=Rc\,{{Z}^{2}}\,\left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right)
finally \frac{1}{\lambda }=R\,{{Z}^{2}}\,\left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right)
Here \frac{1}{\lambda } is called Wave number and is defined as the number of waves per unit length
Number of spectral lines
If an electron jumps from higher energy orbit to lower energy orbit it emits radiation with various spectral lines.
If electron falls from orbit \displaystyle {{n}_{2}} to \displaystyle {{n}_{1}} then the number of spectral lines emitted is given by
{{N}_{E}}=\frac{{({{n}_{2}}-{{n}_{1}}+1)({{n}_{2}}-{{n}_{1}})}}{2}
If electron falls from \displaystyle {{n}^{{\mathbf{th}}}} orbit to ground state (i.e. \displaystyle {{n}_{2}} = n and \displaystyle {{n}_{1}} = 1) then number of spectral lines emitted is given by \displaystyle {{N}_{E}}=\frac{{n(n-1)}}{2}
Spectral series of hydrogen atom or hydrogen Spectrum
When hydrogen atom is excited, it returns to its normal unexcited (or ground state) state by emitting the energy it had absorbed earlier. This energy is given out by the atom in the form of radiations of different wavelengths as the electron jumps down from a higher to a lower orbit. Transition from different orbits cause different wavelengths, these constitute spectral series which are characteristic of the atom emitting them. When observed through a spectroscope, these radiations are imaged as sharp and straight vertical lines of a single colour.
Depending on the order of wavelength of radiations the spectral lines are grouped into a number of series called spectral series.
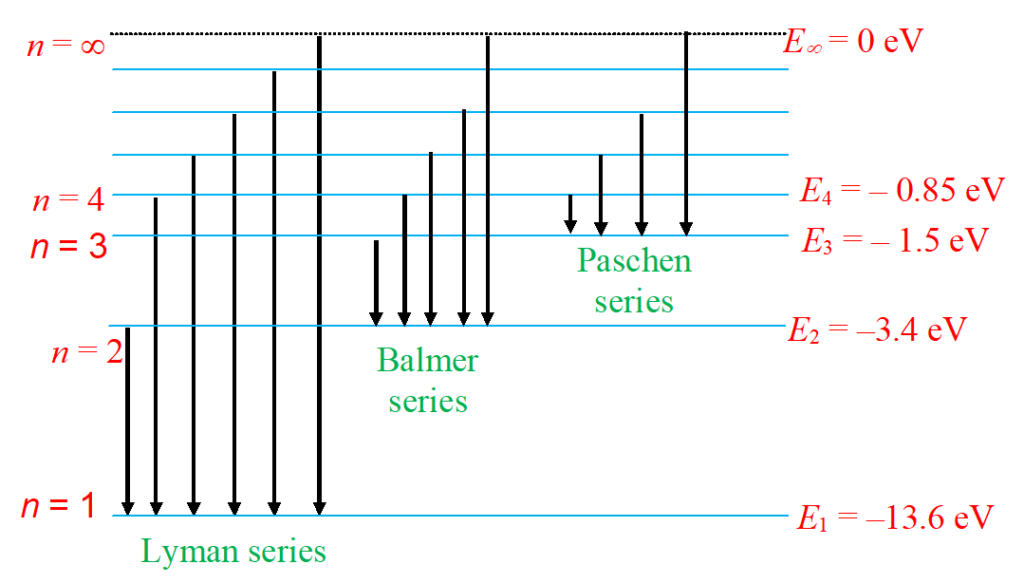
(i) Lyman series
Lyman series is obtained when an electron jump to the first orbit ( \displaystyle {{n}_{1}} = 1) from any outer orbit ( \displaystyle {{n}_{2}} = 2, 3, 4 …)
Wavelength of spectral lines of Lyman series are calculated by using
\frac{1}{\lambda }=R\left[ {\frac{1}{{{{1}^{2}}}}-\frac{1}{{n_{2}^{2}}}} \right], —–(1)
where \displaystyle {{n}_{2}} = 2, 3, 4 …
When \displaystyle {{n}_{2}} = 2, it is the first member of the series.
When \displaystyle {{n}_{2}} = 3, it is the second member of the series and so on.
Calculation of longest wavelength in Lyman Series
For longest wavelength in Lyman series put {{n}_{2}}=2 in above equation number (1)
we get \frac{1}{\lambda }=R\left[ {\frac{1}{{{{1}^{2}}}}-\frac{1}{{{{2}^{2}}}}} \right],
\Rightarrow \lambda =\frac{4}{{3R}}, (As \displaystyle \frac{1}{R}=912{\AA}),
hence \lambda \text{=1216}{\AA} (It is the longest wavelength of Lyman series)
For Shortest wavelength also called Series limit take {{n}_{2}}=\infty in equation (1)
we get \frac{1}{\lambda }=R\left[ {\frac{1}{{{{1}^{2}}}}-\frac{1}{\infty }} \right],\,\,\,\,\,\,\,\Rightarrow \lambda =\frac{1}{R}.
\displaystyle \lambda = 912 \displaystyle {{A}^{o}}.
(It is the shortest wavelength of Lyman series)
All the wavelengths of Lyman series lie in the U.V. region of the spectrum.
(ii) Balmer series
Balmer series is obtained when an electron jumps to the second orbit ( \displaystyle {{n}_{1}} = 2) from any outer orbit ( \displaystyle {{n}_{2}} = 3, 4, 5…).
Wavelengths of these spectral lines are calculated by using
\frac{1}{\lambda }=R\left[ {\frac{1}{{{{2}^{2}}}}-\frac{1}{{n_{2}^{2}}}} \right],
where \displaystyle {{n}_{2}} = 3, 4, 5…
When \displaystyle {{n}_{2}} = 3, it is the first member of the series
When \displaystyle {{n}_{2}} = 4, it is the second member of the series and so on.
To calculate the longest wavelength,putting \displaystyle {{n}_{2}} = 3,
hence \displaystyle \lambda = 6536 \displaystyle {{A}^{o}}.
To calculate the shortest wavelength (series limit) putting \displaystyle {{n}_{2}} = \displaystyle \infty ,
we get \displaystyle \lambda = 3648 \displaystyle {{A}^{o}}.
All the wavelengths of Balmer series lie in the visible region of the spectrum.
(iii) Paschen series
Paschen series is obtained when an electron jumps to the \displaystyle {{3}^{{rd}}} orbit ( \displaystyle {{n}_{1}} = 3) from any outer orbit ( \displaystyle {{n}_{2}}= 4, 5, 6).
Wavelengths are calculated using equation
\frac{1}{\lambda }=R\left[ {\frac{1}{{{{3}^{2}}}}-\frac{1}{{n_{2}^{2}}}} \right],
where \displaystyle {{n}_{2}} = 4, 5, 6…
When \displaystyle {{n}_{2}} = 4, it is the first member of the series and so on.
For Longest wavelength (putting \displaystyle {{n}_{2}} = 4),
we get \displaystyle \lambda = 18761 \displaystyle {{A}^{o}}.
For Shortest wavelength (series limit) (putting \displaystyle {{n}_{2}} = \displaystyle \infty ),
we get \displaystyle \lambda = 8208 \displaystyle {{A}^{o}}.
All the wavelengths of Paschen series lie in the infra-red region of the spectrum.
(iv)Brackett Series
Brackett series is obtained when an electron jumps to the \displaystyle {{4}^{{th}}} orbit ( \displaystyle {{n}_{1}} = 4) from any outer orbit ( \displaystyle {{n}_{2}} = 5, 6, 7…)
Wavelengths are calculated using equation
\frac{1}{\lambda }=R\left[ {\frac{1}{{{{4}^{2}}}}-\frac{1}{{n_{2}^{2}}}} \right],
where \displaystyle {{n}_{2}} = 5, 6, 7…
When \displaystyle {{n}_{2}} = 5, it is the first member of the series
When \displaystyle {{n}_{2}} = 6, it is the second member of the series and so on.
For Longest wavelength putting \displaystyle {{n}_{2}} = 5,
we get \displaystyle \lambda = 40533 \displaystyle {{A}^{o}}
For shortest wavelength (or Series limit) putting \displaystyle {{n}_{2}} = \displaystyle \infty ,
we get \displaystyle \lambda = 14592 \displaystyle {{A}^{o}}.
All these wavelengths lie in the far infra red region of the spectrum.
(v) Pfund series
According to Bohr, it is obtained when an electron jumps to the \displaystyle {{5}^{{th}}} orbit ( \displaystyle {{n}_{1}} = 5) from any outer orbit ( \displaystyle {{n}_{2}} = 6, 7, 8…)
The wavelengths are calculated using the following equation
\frac{1}{\lambda }=R\left[ {\frac{1}{{{{5}^{2}}}}-\frac{1}{{n_{2}^{2}}}} \right],
where, \displaystyle {{n}_{2}} = 6, 7, 8…
When \displaystyle {{n}_{2}} = 6, it is the first member of the series
When \displaystyle {{n}_{2}} = 7, it is the second member of the series and so on.
For Longest wavelength putting \displaystyle {{n}_{2}} = 6,
we get \displaystyle \lambda = 74618 \displaystyle {{A}^{o}}.
For shortest wavelength (series limit) putting \displaystyle {{n}_{2}} = \displaystyle \infty ,
we get \displaystyle \lambda = 22800 \displaystyle {{A}^{o}}.
All these wavelengths lie in the far infrared region of the spectrum.
Important Points:
(i)
The corresponding wavelengths for hydrogen like atoms such as \displaystyle H{{e}^{+}}, \displaystyle L{{i}^{++}}, \displaystyle N{{a}^{+10e}}, are obtained by multiplying the wavelengths for hydrogen atom by \frac{1}{{{{Z}^{2}}}}.
(ii)
If electron from \displaystyle {{n}^{{\mathbf{th}}}} orbit drops back to first orbit then number of lines emitted =\frac{{n(n-1)}}{2}. If electron drops from \displaystyle {{15}^{{th}}} orbit to \displaystyle {{5}^{{th}}} orbit we can convert this transition virtually from \displaystyle {{11}^{{th}}} orbit to \displaystyle {{1}^{{st}}} orbit and use the same formula for calculating the number of line produced.
Figure below shows schematically the allowed orbits together with the energies of the hydrogen atom. It also shows the allowed energies separately.
Drawbacks of bohr’s Model
Following are few important drawbacks of Bohr’s model:
(i)
Hydrogen spectrum when seen under an instrument of high resolving power, it is found that a single line is composed of 2 or 3 closed components. This is known as the find structure of spectral lines. Bohr’s model could not explain these multiple lines .
(ii)
Variations in the intensity of spectrum lines was not explained.
(iii)
Distribution of electrons is atom was not explained.
(iv)
Could not interpret optical spectra of atoms containing more than 1 electron.
(v)
No theoretical basis for selecting the orbits, which had angular momentum an integral multiple of \frac{h}{{2\pi }}.
(vi)
Did not take into account the wave properties of electron.
(vii)
Did not explain the shape of the orbits of electrons.
RECOIL OF ATOM WHEN IT EMIT A PHOTON
When an atom emits a photon due to transition of electron from a higher energy level to a lower energy level, the process is similar to the explosion of bomb that we studied in mechanics. When this occur in a stationary atom, it moves in a direction opposite to that of photon emitted by it. As the process is due to internal changes in the atom hence conservation of linear momentum and energy is applicable.
Let a stationary atom emits a photon of wavelength \displaystyle \lambda . We know that the momentum of the photon is given by p=\frac{h}{\lambda }.
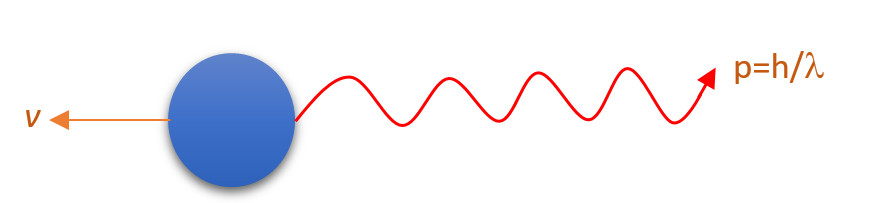
Let as a result of emission of photon the atom recoils with a speed v.
Initial linear momentum of the system before emission of photon is \displaystyle {{p}_{i}} =0 .
Final linear momentum of the system just after the emission of photon is \displaystyle {{p}_{f}}.
Where \displaystyle {{p}_{f}}=\text{ }{{p}_{{atom}}}+\text{ }{{p}_{{photon}}}
or {{p}_{f}}=mv+\frac{h}{\lambda }
Applying conservation of linear momentum i.e. \displaystyle {{p}_{i}}=\text{ }{{p}_{f}}
we get 0=mv+\frac{h}{\lambda }
or mv=-\frac{h}{\lambda } ….. (1)
-ve sign only indicates that the velocity of atom is opposite to the motion of photon otherwise the magnitude of momentum of atom and that of photon is equal.
Let E = energy of liberated photon
Applying conservation of energy i.e. \displaystyle {{E}_{i}}=\text{ }{{E}_{f}}
Where \displaystyle {{E}_{i}} = E (Because initially the energy of liberated photon was inside the atom)
and \displaystyle {{E}_{f}}=\text{ }{{E}_{{atom}}}+\text{ }{{E}_{{photon}}}
hence {{E}_{f}}=\frac{1}{2}m{{v}^{2}}+\frac{{hc}}{\lambda }
since \displaystyle {{E}_{i}}=\text{ }{{E}_{f}}
therefore E=\frac{1}{2}m{{v}^{2}}+\frac{{hc}}{\lambda }
Since atom is very heavy so its speed and hence kinetic energy can be taken as very small as compared to that of photon. So the kinetic energy of the atom can be neglected.
Hence E=\frac{{hc}}{\lambda } ( from equation no.(1) \frac{h}{\lambda }=mv\text{ in magnitude})
so E=mvc and hence finally
v=\frac{E}{{mc}}
This is the speed of recoil of an atom of mass m which has emitted a photon of energy E
Excitation of Hydrogen atom by collision with a neutron
If a neutron collides head on with a stationary hydrogen atom three possibilities arise
1.
The collision may be perfectly elastic
2.
The collision may be perfectly inelastic
3.
The collision may be partially inelastic also called inelastic collision.
Due to collision the atom can be excited only if there is a loss of energy during the collision. The energy lost is actually absorbed by the atom to get excited. In other words the electrons in the atom absorb this energy and goes to the higher energy states. If the energy loss is not sufficient to send the electron to next energy level then this energy will remain in the form of kinetic energy of the colliding particles.
Perfectly elastic collision
We know that when two equal masses collide head on elastically then their velocities get interchanged. Since the mass of neutron and hydrogen atom is almost same so here also the velocities of two particles will interchange as shown in the diagram given below.

Since the initial and final kinetic energy of the system of two particles remains equal hence there is no loss of kinetic energy and hence excitation of hydrogen atom is not possible in this collision
Perfectly inelastic collision
We know that in this case maximum loss of kinetic energy takes place. Lets calculate the maximum loss of kinetic energy when a neutron collide head on with a hydrogen atom.
Applying conservation of linear momentum
mv+0=mv’+mv’
(remember \displaystyle {{m}_{{neutron}}}=\text{ }{{m}_{{hydrogen}}} = m)
\Rightarrow \text{ }mv=2mv’
or \Rightarrow \text{ }v’=\frac{v}{2}
Let \displaystyle \Delta E be the loss in kinetic energy then \displaystyle \Delta E=\text{ }K{{E}_{{initial}}}\text{ }-K{{E}_{{final}}}. Remember that \displaystyle \Delta E is the energy available for excitation of atom.
where \text{K}{{\text{E}}_{{initial}}}\text{=}\frac{1}{2}m{{v}^{2}}+0
and K{{E}_{{final}}}=\frac{1}{2}m{{{v}^{\prime}}^{2}}+\frac{1}{2}m{{{v}^{\prime}}^{2}}
therefore K{{E}_{{final}}}=\frac{1}{2}m{{\left[ {\frac{v}{2}} \right]}^{2}}+\frac{1}{2}m{{\left[ {\frac{v}{2}} \right]}^{2}}
so K{{E}_{final}}=\frac{1}{4}m{{v}^{2}} (because \text{ }v’=\frac{v}{2})
Since \Delta E=\text{K}{{\text{E}}_{{initial}}}-K{{E}_{{final}}}
hence \Delta \text{E=}\frac{1}{2}m{{v}^{2}}-\frac{1}{4}m{{v}^{2}}
\Rightarrow \text{ }\Delta \text{E=}\frac{1}{4}m{{v}^{2}}=\frac{1}{2}K{{E}_{{initial}}}
So we have seen that half of the kinetic energy of neutron is lost during the collision. Now this energy is absorbed by the hydrogen atom to get excited.
Minimum K.E. of neutron required to excite the hydrogen atom
To just excite a hydrogen atom from ground state i.e.n=1 to n=2 level the energy required is 10.2eV.
Hence during the collision if \displaystyle \Delta E =10.2 eV then the hydrogen atom will get excited from n=1 to n=2 level.
Hence \displaystyle \Delta E =10.2 eV
or \frac{1}{2}K{{E}_{{initial}}}=10.2
therefore K{{E}_{{initial}}}=20.4eV
So to just excite a hydrogen atom from n=1 to n=2, the colliding neutron must have at least 20.4eV of energy.
To excite the hydrogen from n=1 to n=3 level how much energy must the neutron have?
Answer is that fro transition from n=1 to n=3 the energy required is 13.6-1.5= 12.1eV.
So loss in energy i.e. \displaystyle \Delta E must be at least equal to 12.1eV
Hence \displaystyle \Delta E =12.1eV
or \frac{1}{2}K{{E}_{{initial}}}=12.1
therefore K{{E}_{{initial}}}=24.2eV.
So to excite a hydrogen atom from n=1 to n=3, the colliding neutron must have at least 24.2eV of energy.
Important Point:
Just now we have seen that to excite the atom from n=1 to n=2 level the loss of energy \displaystyle \Delta E must be 10.2eV. And for n=1 to n=3, \displaystyle \Delta E must be 12.1eV. Now what happens if \displaystyle \Delta E is lying between the two values like if \displaystyle \Delta E is 11.5eV?
Answer is in that case the atom will absorb 10.2eV and get excited from n=1 to n=2, whereas the remaining energy will remain with the particles as their kinetic energies. Hence the collision is not perfectly inelastic but it can be said as partially inelastic
Illustration
The longest wavelength in the Lyman series for hydrogen is 1215 \displaystyle {{A}^{o}}. Calculate the Rydberg constant.
Solution
\frac{1}{\lambda }=R\ \left( {\frac{1}{{n_{l}^{2}}}-\frac{1}{{n_{u}^{2}}}} \right)
For the Lyman series \displaystyle {{n}_{l}} = 1; the longest wavelength will correspond to the value \displaystyle {{n}_{u}} = 2.
\frac{1}{{1215{\AA}}}=R\ \left( {\frac{1}{{{{1}^{2}}}}-\frac{1}{{{{2}^{2}}}}} \right)
or R = \displaystyle 1.097\times {{10}^{{-3}}}{{{\AA}}^{{-1}}}
Illustration
How many different photons can be emitted by hydrogen atoms that undergo transitions to the ground state from the n = 5 state?
Solution
Consider the problem for arbitrary n. If \displaystyle {{n}_{u}}>{{n}_{l}} is any pair of unequal integers in the range 1 to n, it is clear that there is at least one route from state n down to the ground state that includes the transition \displaystyle {{n}_{u}}\to {{n}_{l}}. Thus, the number of photons is equal to the number of such pairs, which is \left( {_{2}^{n}} \right)=\frac{{n\ (n-1)}}{2}
For n = 5, there are 5(4)/2 = 10 photons.
Illustration
A single electron orbits around a stationary nucleus of charge +Ze, where Z is a constant and e is the magnitude of electronic charge. It requires 47.2 eV to excite the electron from second Bohr orbit to the third Bohr orbit.
(a) Find the value of Z
(b) Find the energy required to excite the electron from n = 3 to n = 4
(c) Find the wavelength of radiation required to remove electron from first Bohr’s Orbit to infinity.
(d) Find the kinetic energy, potential energy and angular momentum of the electron in the first Bohr orbit.
Solution
(a) Given \displaystyle \Delta {{E}_{{23}}}= 47.2 eV
Since \displaystyle \Delta E=\text{ }13.6 \times {{Z}^{2}} \left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right) eV
or 47.2 = \displaystyle 13.6 \times {{Z}^{2}} \left( {\frac{1}{{{{2}^{2}}}}-\frac{1}{{{{3}^{2}}}}} \right)
hence Z = 5
(b) To find \displaystyle \Delta {{E}_{{34}}}, put \displaystyle {{n}_{1}} = 3 and \displaystyle {{n}_{2}} = 4
\displaystyle \Delta E=\text{ }13.6 \times {{Z}^{2}} \left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right) eV
or {\Delta}E= \displaystyle 13.6 \times {{{5}^{2}}} \left( {\frac{1}{{{{3}^{2}}}}-\frac{1}{{{{4}^{2}}}}} \right)
hence {\Delta}E = 16.53 eV
(c) Ionization energy is the energy required to excite the electron from n = 1 to n = \displaystyle \infty
Thus, {\Delta}E= \displaystyle 13.6 \times {{{5}^{2}}} \left( {\frac{1}{{{{1}^{2}}}}-\frac{1}{{{{\infty }^{2}}}}} \right)
so {\Delta}E= 340 eV
The respective wavelength is
\displaystyle \lambda = \frac{{hc}}{{\Delta E}}= \frac{{12400}}{{\Delta E}}=\frac{{12400}}{{340}}
hence \displaystyle \lambda = 36.47 {{A}^{o}}
(d) we know for an electron , according to Bohr’s Theory, kinetic energy K, Potential energy U and Total energy E are related as
K= – E and U = 2E
Hence K = –E = +340 eV
and U = 2E = -680 eV
we know that angular momentum is given by L = \frac{nh}{{2\pi }}
hence L= \frac{{1 \times 6.63\times {{{10}}^{{-34}}}}}{{2\pi }}
so L = \displaystyle 1.056\times {{10}^{{-34}}}J-s
Illustration
Find the quantum number n corresponding to excited state of He+ ion if on transition to the ground state, the ion emits two photons in succession with wavelengths 108.5 nm and 30.4 nm. The ionization energy of H atom is 13.6 eV.
Solution
The energy transitions for the given wavelengths are
\displaystyle \Delta {{E}_{1}} = \frac{{12400}}{{{{\lambda }_{1}}}}=\frac{{12400}}{{1085}}=11.43eV
\displaystyle \Delta {{E}_{2}} = \frac{{12400}}{{{{\lambda }_{2}}}}=\frac{{12400}}{{304}}\,
\displaystyle \Delta {{E}_{2}}= 40.79 eV
Total energy emitted \displaystyle \Delta E=\Delta {{E}_{1}}+\Delta {{E}_{2}} = 52.22 eV
we know that energy emitted is given by
\displaystyle \Delta E=\text{ }13.6{{Z}^{2}} \left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right) eV
or \displaystyle 52.22 = 13.6 \times {{5}^{2}} \left( {\frac{1}{{{{1}^{2}}}}-\frac{1}{{{{n}^{2}}}}} \right)
Thus, n = 5
Illustration
An isolated hydrogen atom emits a photon of 10.2 eV.
(a) Determine the momentum of photon emitted
(b) Calculate the recoil momentum of the atom
(c) Find the kinetic energy of the recoil atom.
[Given mass of proton, \displaystyle {{m}_{P}}=\text{ }1.67\times {{10}^{{-27}}}kg]
Solution
(a) Momentum of the photon is
{{p}_{1}} = \frac{E}{c} = \frac{{10.2\times 1.6\times {{{10}}^{{-19}}}}}{{3\times {{{10}}^{8}}}}
thus {{p}_{1}} = 5.44 \times {{10}^{-27}} kg m/s
(b) Applying the momentum conservation
\displaystyle {{p}_{2}}={{p}_{1}}=5.44\times {{10}^{{-27}}}kg m/s
(c) K = \frac{1}{2}m{{v}^{2}} (v = recoil speed of atom, m = mass of hydrogen atom)
or K = \frac{1}{2}m{{\left( {\frac{p}{m}} \right)}^{2}}=\frac{{{{p}^{2}}}}{{2m}}
Substituting the value of the momentum of atom, we get
K = \frac{{{{{\left( {5.44\times {{{10}}^{{-27}}}} \right)}}^{2}}}}{{2\times 1.67\times {{{10}}^{{-27}}}}}
thus K = \displaystyle 8.86\times {{10}^{{-27}}}J
Illustration
A hydrogen atom in a state of binding energy 0.85 eV makes a transition to a state of excitation energy of 10.2 eV. Find the energy and wavelength of photon emitted.
Solution
Since the binding energy is always negative, therefore,
\displaystyle {{E}_{i}} = -0.85 eV
Let \displaystyle {{n}_{i}} be the initial binding state of the electron, then
\displaystyle {{E}_{n}} = -13.6\frac{{{{Z}^{2}}}}{{n_{i}^{2}}}
or -0.85 = -13.6 \frac{{{{Z}^{2}}}}{{n_{i}^{2}}}
or \displaystyle {{n}_{i}} = 4
we know that Binding energy = \displaystyle {{E}_{n}}=\text{ }-13.6\text{ }{{Z}^{2}}/{{n}^{2}}
hence -0.85 eV = -13.6 \displaystyle {{\left( 1 \right)}^{2}}/{{n}_{2}}^{2}~~
thus \displaystyle {{n}_{2}} = 4
Let the electron now goes to an energy level n whose excitation energy is 10.2 eV. Since the excitation energy \displaystyle \Delta E is defined with respect to ground state, therefore
\displaystyle \Delta E=\text{ }13.6{{Z}^{2}} \left( {\frac{1}{{n_{1}^{2}}}-\frac{1}{{n_{2}^{2}}}} \right) eV
or 10.2 = \displaystyle 13.6 \times {{\left( 1 \right)}^{2}} \left( {\frac{1}{{{{1}^{2}}}}-\frac{1}{{n_{f}^{2}}}} \right)
thus \displaystyle {{n}_{f}} = 2
So the electron makes a transition from energy level \displaystyle {{n}_{i}} = 4 to \displaystyle {{n}_{f}} = 2.
Thus, the energy released is \displaystyle \Delta E={{E}_{4}}-{{E}_{2}}
or {\Delta}E = 13.6 \times \left[ {\frac{1}{{{{2}^{2}}}}-\frac{1}{{{{4}^{2}}}}} \right] = 2.55 eV
Since \displaystyle \lambda= \frac{{hc}}{{\Delta E}}
hence \displaystyle \lambda = \frac{{12400}}{{2.25eV}}=5511 {{A}^{o}}
Illustration
A particle of charge equal to that of an electron, –e and mass 208 times the mass of electron (called a \displaystyle \mu -meson) moves in a circular orbit around a nucleus of charge +3e (take the mass of the nucleus to be infinite). Assuming that the Bohr model of the atom is applicable to this system:
(i) Calculate the radius of nth Bohr orbit
(ii) Find the value of n, for which the radius of orbit is approximately the same as that of first Bohr orbit for the hydrogen atom;
(iii) Find the wavelength of radiation emitted when the m-meson jumps from the third orbit to first orbit
(Rydberg’s constant = \displaystyle 1.097\times {{10}^{7}}/m)
Solution
(i) Radius of the nth Bohr orbit for hydrogen atom is
\displaystyle {{r}_{n}}= 0.53\times \frac{{{{n}^{2}}}}{Z}
Since r \propto \frac{1}{m}
Radius of nth orbit for \displaystyle \mu -meson is
\displaystyle {{r}_{n}} = \frac{{0.53{{n}^{2}}}}{{\left( {208} \right)Z}}
or \displaystyle \displaystyle {{r}_{n}}= (8.5\times {{10}^{{-4}}}){{n}^{2}}
(ii) \displaystyle (8.5\times {{10}^{{-4}}}){{n}^{2}}= 0.53
or \displaystyle {{n}^{2}} = 623
hence n » 25
(iii) In case of hydrogen like atom,
\displaystyle \Delta E={{E}_{3}}-{{E}_{1}}=\text{ }13.6{{Z}^{2}} \left( {1-\frac{1}{{{{3}^{2}}}}} \right)
so \displaystyle \Delta E= 12.08 eV
since {\Delta}E \displaystyle \propto m
so for \displaystyle \mu -meson, {\Delta}E= (12.8)(208) = 22.6 keV
Since \displaystyle \lambda = \frac{{12400}}{{\Delta E}}=\frac{{12400}}{{22.6\times {{{10}}^{3}}}}\,
so \displaystyle \lambda= 0.548 {{A}^{o}}
Practice Questions (Basic Level)
1.
In a head-on collision between an a-particle and a gold nucleus, the minimum distance of approach is 3.95 × 10–14 m. Calculate the energy of the a-particle.
(a) 1MeV
(b) 6MeV
(c) 2MeV
(d) 10MeV
Ans (b)
2.
In an atom, two electrons move around the nucleus in circular orbits of radii R and 4R. The ratio of the time taken by them to complete one revolution is
(a) \frac{1}{4}
(b) \frac{4}{1}
(c) \frac{8}{1}
(d) \frac{1}{8}.
Ans (d)
3.
The kinetic energy of the electron in an orbit of radius r in hydrogen atom is (e = electronic charge)
(a) \frac{{{{e}^{2}}}}{{{{r}^{2}}}}
(b) \frac{{{{e}^{2}}}}{{2r}}
(c) \frac{{{{e}^{2}}}}{r}
(d) \frac{{{{e}^{2}}}}{{2{{r}^{2}}}}.
Ans (b)
4.
A charged oil drop is suspended in a uniform electric field of 3 × 104 Vm–1, so that it neither falls nor rises. Find the charge on the drop if its mass is 9.75 × 10–15kg.
(a) 4.7 × 10–12 C
(b) 3.8 × 10–12 C
(c) 3.2 × 10–12 C
(d) 2.6 × 10–12 C
Ans (c)
5.
The angular momentum of an electron in a hydrogen atom is proportional to
(a) \frac{1}{{\sqrt{r}}}
(b) \frac{1}{r}
(c) \sqrt{r}
(d)r2.
Ans (c)
6.
One requires an energy En to remove a nucleon from a nucleus and an energy Ee to remove an electron from an atom. Then
(a) {{E}_{n}}={{E}_{e}}
(b) {{E}_{n}}<{{E}_{e}}
(c) {{E}_{n}}>{{E}_{e}}
(d) {{E}_{n}}\ge {{E}_{e}}.
Ans (c)
7.
Calculate the second excitation potential of single ionized helium.
Given e = 1.6×10–19 C, m = 9.1 10–31 kg and h = 6.62 10–34 J-s.
(a) 6.2 eV
(b) 5.4 eV
(c) 6.9 eV
(d) 7.7 eV
Ans (a)
8.
As per Bohr model, the minimum energy (in eV) required to remove an electron from the ground state of doubly ionized Li and (Z = 3) is
(a) 1.51
(b) 13.6
(c) 40.8
(d) 122.4
Ans (d)
9.
In Bohr’s model, the atomic radius of the first orbit is r0, then the radius of the third orbit is
(a) \frac{{{{r}_{0}}}}{9}
(b) {{r}_{0}}
(c) 9{{r}_{0}}
(d) 3{{r}_{0}}
Ans (c)
10.
As per Bohr model, the minimum energy (in eV) required to remove an electron from the ground state of doubly ionized Li and (Z = 3) is
(a) 1.51
(b) 13.6
(c) 40.8
(d) 122.4
Ans (d)
11.
A gas of hydrogen like atoms can absorb radiations of 68 eV. Consequently, the atoms emit radiations of only three different wavelengths. All the wavelengths are equal or smaller than that of the absorbed photon.
(a)
Determine the initial state of the gas atoms.
(a) 28.5 Å
(b) 46.3 Å
(c) 1.7 Å
(d) 3.4 Å
Ans (a)
(b)
Identify the gas atoms.
(a) n = 2, Z = 9
(b) n = 2, Z = 1
(c) n = 2, Z = 2
(d) n = 2, Z = 6
Ans (d)
(c)
Find the minimum wavelength of the emitted radiations.
(a) 25.32 Å ,
(b) 0.76 Å
(c) 2.3 Å
(d) 12.3 Å
Ans (a)
(d)
Find the ionization energy and the respective wavelength for the gas atoms.
(a) 450.2 eV
(b) 489.6 eV
(c) 328.4 eV
(d) 423.5 eV
Ans (b)
12.
A 100-W bulb converts 5% of the electrical energy input to visible light. Assume the light has a wavelength of 600 nm and the bulb is a point source.
(a)
What is the number of photons emitted per second?
(a) 1.51 x 1019s-1
(b) 0.51 x 1019s-1
(c) 4.51 x1019s-1
(d) 9.51 x1019s-1
Ans (a)
(b)
If the eye can detect 20 photons/s, at what distance would the bulb be visible? Take the pupil diameter to be 3 mm.
(a) 700 km
(b) 38 km
(c) 150 km
(d) 652 km
Ans (d)
13.
A hydrogen atom emits radiation of wavelength 102.5 nm. What are the n values of the two levels involved?
(a) n = 1, 1
(b) n = 1, 3
(c) n = 1, 2
(d) n = 1, 9
Ans (b)
14.
The electron in the hydrogen atom is in the n = 2 state. What is its
(a) potential energy
(a) – 6.8 eV
(b) – 6.2 eV
(c) – 7.4 eV
(d) -2.5 eV
Ans (a)
(b)
kinetic energy?
(a) 0.3 eV
(b) 3.4 eV
(c) 9.2 eV
(d) 11.5 eV
Ans (b)
15.
What is the maximum wavelength that can ionize a hydrogen atom in the ground state? In what region of the electromagnetic spectrum does this wavelength lie?
(a) 20.5 nm
(b) 55.3 nm
(c) 73.9 nm
(d) 91.2 nm
Ans (d)
16.
What is the shortest wavelength
(a)
in the Balmer series
(a) 2000 Å
(b) 3050 Å
(c) 3650 Å
(d) 4000 Å
Ans (c)
(b)
in the Lyman series?
(a) 914 Å
(b) 948 Å
(c) 1000 Å
(d) 2000 Å
Ans (a)
17.
The wavelength of first line of Balmer series of hydrogen is 6562.8Å. Calculate the ionization potential of hydrogen atom.
(a) 13.26 V
(b) 14.22 V
(c) 12.33 V
(d) 13.62 V
Ans (d)
18.
A gas of hydrogen atoms in their ground state is bombarded by electrons with kinetic energy 12.5 eV. What emitted wavelengths would you expect to see?
(a) 102 nm; 122 nm; 238 nm
(b) 102 nm; 134 nm; 600 nm
(c) 102 nm; 122 nm; 653 nm
(d) 104 nm; 126 nm; 640 nm
Ans (c)
19.
The radius of Bohr’s first orbit is a0. The electron in nth orbit has a radius
(a)na0
(b) \frac{{{{a}_{0}}}}{n}
(c)n2a0
(d) \frac{{{{a}_{0}}}}{{{{n}^{2}}}}.–
Ans (c)
20.
The ratio of the speed of the electrons in the ground state of hydrogen to the speed of light in vacuum is
(a) \frac{1}{2}
(b) \frac{2}{{237}}
(c) \frac{1}{{237}}
(d) \frac{1}{{237}}
Ans (d)
Practice Questions (JEE Main Level)
1.
What is the impact parameter at which the scattering angle is 90° for Z = 79 and initial energy of the a-particle is 10 MeV?
(a)2.7 × 10–14m
(b) 0.7 × 10–14m
(c) 1.1 × 10–14m
(d) 1.8 × 10–14m
Ans (c)
2.
If the electron in H atom radiates a photon of wavelength 4860 Å, the kinetic energy of the electron
(a) decreases by 2.0 × 10–19J
(b) increases by 4.1 × 10–19J
(c) decreases by 4.1 × 10–19J
(d) increases by 8.2 × 10–19J.
Ans (c)
3.
A stream of electrons moving with a speed of 3 × 107 ms–1 is deflected on passing through an electric field of 1800 Vm–1, perpendicular to its path. If the radius of the deflected beam is 3 m, calculate the value of e/m.
(a) 1.7 × 1011 Ckg–1
(b) 0.5 × 1011 Ckg–1
(c) 2.4 × 1011 Ckg–1
(d) 3.7 × 1011 Ckg–1
Ans (a)
4.
An oil drop carrying a charge of 2e is kept stationary between two horizontal plates 2.0 cm apart when a potential difference of 12000V is applied across them. Calculate the radius of the drop. Density of oil 1200 kg m–3 and g = 9.8 ms–2.
(a) 1.2 × 10–6m
(b) 0.3 × 10–6m
(c) 2.8 × 10–6m
(d) 1.7 × 10–6m
Ans (d)
5.
Electrons in hydrogen atom revolve in radius 0.53 Å (in ground state). Due to collision, electron starts revolving in radius of 4.77 Å. Change in angular momentum of the electron will be equal to
(a) 2.11 × 10–36 kg m2/sec
(b) 4.22 × 10–30 g m2/sec
(c) 2.11 × 10–27 g cm2/sec
(d) 4.22 × 10–36 kg m2/sec
Ans (c)
6.
In the hydrogen atom spectrum, {{\lambda}_{3-1}} and {{\lambda}_{2-1}} represent wavelengths emitted due to transition from second and first excited states to the ground state respectively. The value of \frac{{{{\lambda }_{{3-1}}}}}{{{{\lambda }_{{2-1}}}}} is
(a) \frac{{27}}{{32}}
(b) \frac{{32}}{{27}}
(c) \frac{4}{9}
(d) \frac{9}{4}
Ans (a)
7.
In terms of the Bohr’s radius a0 the radius of the second Bohr orbit of hydrogen atom is given by
(a)4 a0
(b)8 a0
(c) \sqrt{2}\,{{a}_{0}}
(d)2 a0.
Ans (a)
8.
Which of the following curves may represent the speed of electron in a hydrogen atom as a function of principal quantum number n?
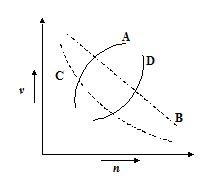
(a) A
(b) B
(c) C
(d) D
Ans (c)
9.
In hydrogen like atoms the ratio of difference of energies {{E}_{{4n}}}-{{E}_{{2n}}} and {{E}_{{2n}}}-{{E}_{n}} varies with atomic number z and principle quantum number n as
(a) \frac{{{{z}^{2}}}}{{{{n}^{2}}}}
(b) \frac{{{{z}^{4}}}}{{{{n}^{4}}}}
(c) \frac{z}{n}
(d) none of these
Ans (d)
10.
The radius of hydrogen atom in its ground state is 5.3 × 10–11 m. After collision with an electron it is found to have a radius of 21.2 × 10–11 m. What is the principal quantum number n of the final state of the atom?
(a) n = 4
(b) n = 2
(c) n = 16
(d) n = 3
Ans (b)
11.
An electron in H-atom jumps from second excited state to first excited state and then from first excited to ground state. Let the ratio of wavelength, momentum and energy of photons emitted in these two cases be a, b and c respectively. Then, choose the incorrect answer:
(a) c=\frac{1}{a}
(b) a=\frac{9}{4}
(c) b=\frac{5}{{27}}
(d) c=\frac{5}{{27}}
Ans (b)
12.
What is the ratio of the circumference of the first Bohr orbit for the electron in the hydrogen atom to the de-Broglie wavelength of electrons having the same velocity as the electron in the first Bohr orbit of the hydrogen atom?
(a) 1 : 1
(b) 1 : 2
(c) 1 : 4
(d) 2 : 1
Ans (a)
13.
In a hydrogen atom, an electron of mass m and charge e is in an orbit of radius r making n revolutions per second. If the mass of the hydrogen nucleus is M , the magnetic moment associated with the orbital motion of the electron is
(a) \frac{{\pi ne{{r}^{2}}m}}{M}
(b) \frac{{\pi ne{{r}^{2}}M}}{m}
(c) \frac{{\pi ne{{r}^{2}}m}}{{\left( {M+m} \right)}}
(d) \pi ne{{r}^{2}}
Ans (d)
14.
The hydrogen atoms in its ground state are excited by means of monochromatic radiations of wavelength 1023 Å. The number of lines which can be seen in the resulting spectrum is
(a) 1
(b) 2
(c) 3
(d) 6
Ans (c)
15.
In hydrogen atom, if potential energy of electron in ground state is assumed to be zero, then its energy in first excited state is equal to
(a) – 3.4 eV
(b) 23.8 eV
(c) 17.2 eV
(d) – 6.8 eV
Ans (b)
16.
If an electron in an hydrogen atom jumps from an orbit ni = 3 to an orbit with level nf = 2, the frequency of the emitted radiation is
(a) f=\frac{{36c}}{{5R}}
(b) f=\frac{{cR}}{6}
(c) f=\frac{{5Rc}}{{36}}
(d) f=\frac{{6c}}{R}.
Ans (c)
17.
When an electron jumps from an orbit of higher energy E1 to an orbit of lower energy E2, the frequency of radiation occurring is given by
(a) \frac{{({{E}_{1}}-{{E}_{2}})}}{h}
(b) \frac{{({{E}_{1}}+{{E}_{2}})}}{h}
(c) \frac{{{{{({{E}_{1}}-{{E}_{2}})}}^{2}}}}{h}
(d) \frac{{({{E}_{1}}-{{E}_{2}})}}{{{{h}^{2}}}}.
Ans (a)
18.
The first member of Balmer series of H-atom has a wavelength 6561Å . The wavelength of second member will be
(a) 6860 Å
(b) 5860 Å
(c) 4860 Å
(d) 3860 Å
Ans (c)
19.
Energy levels A, B, C of a certain atom correspond to increasing values of energy i.e., \displaystyle {{E}_{A}}<\text{ }{{E}_{B}}<\text{ }{{E}_{C}}. If {{\lambda}_{1}},{{\lambda}_{2}},{{\lambda}_{3}} are the wave lengths of radiation corresponding to the transitions C to B, B to A and C to A respectively, which of the following relations is correct?
(a) {{\lambda }_{3}}={{\lambda }_{1}}+{{\lambda }_{2}}
(b) {{\lambda }_{3}}=\frac{{{{\lambda }_{1}}\,{{\lambda }_{2}}}}{{{\lambda }_{1}}+{{\lambda }_{2}}}
(c) {{\lambda }_{1}}+{{\lambda }_{2}}+{{\lambda }_{3}}=0
(d) \lambda _{3}^{2}=\lambda _{1}^{2}+\lambda _{2}^{2}.
Ans (b)
20.
In which of the following transitions will the wavelength be minimum in the case of hydrogen atom?
(a) n = 5 to n = 4
(b) n = 4 to n = 3
(c) n = 3 to n = 2
(d) n = 2 to n = 1
Ans (d)
21.
The wave number of energy emitted when electron comes from fourth to second orbit in hydrogen is 20397 cm–1. The wave number of energy for same transition in helium is
(a) 5099 cm–1
(b) 20497 cm–1
(c) 40994 cm–1
(d) 81588 cm–1
Ans (d)
22.
An electron collides with a fixed hydrogen atom in its ground state. Hydrogen atom gets excited and the colliding electron loses all its kinetic energy. Consequently the hydrogen atom may emit a photon corresponding to the largest wavelength of the Balmer series. The minimum kinetic energy of colliding electron is
(a) 10.2 eV
(b) 1.9 eV
(c) 12.09 eV
(d) 13.6 eV
Ans (c)
Practice Questions (JEE Advance Level)
1.
The electric potential between a proton and an electron is given by V={{V}_{0}}\ln \frac{r}{{{{r}_{0}}}}, where {{r}_{0}} is a constant. Assuming Bohr’s model to be applicable, then variation of {{r}_{n}} with n, where n being the principal quantum number is
(a) {{r}_{n}}\propto n
(b) {{r}_{n}}\propto \frac{1}{n}
(c) {{r}_{n}}\propto {{n}^{2}}
(d) {{r}_{n}}\propto \frac{1}{{{{n}^{2}}}}
Ans (a)
2.
An electron in hypothetical hydrogen atom is in its 3rd excited state and makes transition from 3rd to 2nd excited, then to 1st excited state and then to ground state. If the amount of time spent by the electron in any state of quantum number n, is proportional to \left( {\frac{1}{{n-1}}} \right), then the ratio of no. of revolutions completed by the electron in 1st excited state to that in the 2nd excited state will be
(a) 2
(b) \frac{{27}}{8}
(c) \frac{{27}}{4}
(d) \frac{{27}}{6}
Ans (c)
3.
Suppose potential energy between electron and proton at separation r is given by U = klnr, where k is constant. For such hypothetical hydrogen atom, the ratio of energy difference between energy levels (n = 1 and n = 2) and (n = 2 and n = 4) is
(a) 1
(b) 2
(c) \frac{1}{2}
(d) 3
Ans (a)
4.
In hydrogen atom, the radius of nth Bohr’s orbit is The graph between log \left( {\frac{{{{r}_{n}}}}{{{{r}_{1}}}}} \right) and log n will be
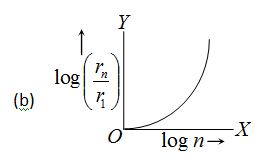
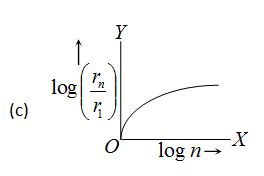
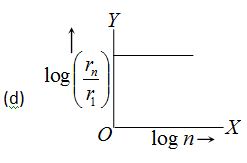
Ans (a)
Question no. 5 to 7
A gas of identical hydrogen like atoms has some atoms in the lowest (ground) energy level A and some atoms in a particular upper (excited) energy level B and there are no atoms in any other energy level. The atoms of the gas make transition to higher energy level by absorbing monochromatic light of photon 2.7 eV. Subsequently, the atoms emit radiation of only six different photon energies. Some of the emitted photons have energy 2.7 eV, some have energy more and some have less than 2.7 eV.
(5)
Find the principal quantum number of the initially excited level B.
(a) Z = 0
(b) Z = 1
(c) Z = 5
(d) Z = 10
Ans (b)
(6)
Find the ionization energy for the gas atoms.
(a) -13.6 eV
(b) -3.23 eV
(c) -4.36 eV
(d) -10.3 eV
Ans (a)
(7)
Find the maximum and the minimum energies of the emitted photons.
(a) 12.75 eV, 0.29 eV
(b) 12.75 eV, 0.33 eV
(c) 12.75 eV, 0.16 eV
(d) 12.75 eV, 0.66 eV
Ans (d)
Question no. 8 to 10
A \mu – meson which is 210 times as heavy as an electron and having charge equal to that of an electron is captured by a proton to form a hydrogen – like atom.
(8)
What is the energy of the photon that is emitted when a \displaystyle \mu – meson falls from the first excited state to the ground state ?
(a) 2122 eV
(b) 2142 eV
(c) 2022 eV
(d) 1187 eV
Ans (b)
(9)
What is the radius of the first Bohr orbit ?
(a) 0.0023 Å
(b) 0.045 Å
(c) 1.0059 Å
(d) 10.67 Å
Ans (a)
(10)
What is the velocity of the \displaystyle \mu – meson in the first circular Bohr orbit ?
(a) 0.36 x 106 m/s
(b) 1.75 x 106 m/s
(c) 2.19 x 106 m/s
(d) 5.67 x 106 m/s
Ans (c)
Question no. 11 to 12
The atom of a positronium consists of an electron and a positron orbiting about each other.
(11)
Find the Bohr radius of this system.
(a) 2.54 Å
(b) 5.38 Å
(c) 0.3 Å
(d) 1.06 Å
Ans (d)
(12)
Find the wavelength of the photon released in the transition from n = 2 to n = 1.
(a) 2235 Å
(b) 2054 Å
(c) 2431 Å
(d) 1235 Å
Ans (c)
Question no. 13 to 14.
A monochromatic light source of frequency f illuminates a metallic surface and ejects photoelectrons. The photoelectrons having maximum energy are just able to ionize the hydrogen atoms in ground state. When the whole experiment is repeated with an incident radiation of frequency \frac{5}{6}f, the photoelectrons so emitted are able to excite the hydrogen atom beam which then emits a radiation of wavelength 1215Å.
(13)
Find the work function of the metal.
(a) 4.35 x 1015Hz
(b) 1.53 x 1015Hz
(c) 0.23 x 1015Hz
(d) 4.92 x 1015Hz
Ans (d)
(14)
What is the frequency of radiation .
(a) 1.3 eV
(b) 6.8 eV
(c) 9.5 eV
(d) 10.8 eV
Ans (b)
15.
A hydrogen like atom (atomic number Z) is in a higher excited state of quantum number n. This excited atom can make a transition to the first excited state by successively emitting two photons of energies 10.20 eV and 17.00 eV respectively. Alternatively, the atom from the same excited state can make a transition to the second excited state by successively emitting two photons of energies 4.25 eV and 5.95 eV respectively. Determine the values of n and Z. (ionization energy of hydrogen atom = 13.6 eV).
(a) n = 3, Z = 6
(b) n = 6, Z = 3
(c) n = – 6, Z = – 3
(d) n =-3, Z = – 6
Ans (b)
16.
A hydrogen atom is in an excited state of principle quantum number n. It emits a photon of wavelength \displaystyle \lambda when returns to the ground state. The value of n is (R = Rydberg constant)
(a) \sqrt{{\lambda R(\lambda R-1)}}
(b) \sqrt{{\frac{{(\lambda R-1)}}{{\lambda R}}}}
(c) \sqrt{{\frac{{\lambda R}}{{\lambda R-1}}}}
(d) \sqrt{{\lambda (R-1)}}
Ans (c)
