Video Lecture
Theory For Notes Making
Lorentz force
The force experienced by a charged particle moving in space where both electric and magnetic fields exist is called Lorentz force.
Force due to electric field: When a charge particle carrying charge +q is subjected to an electric field of strength \vec{E}, it experiences a force given by {{\vec{F}}_{e}}=q\vec{E}. Whose direction is the same at that of \vec{E}.
Force due to magnetic field: IF the charged particle is moving in a magnetic field , with a velocity it experiences a force given by
{{\vec{F}}_{m}}=q(\vec{v}\times \vec{B})
The direction of this force is in the direction of (\vec{v}\times \vec{B}) i.e. perpendicular to the plane containing \vec{v} and \vec{B} and is directed as given by right hand screw rule.
Due to both the electric and magnetic fields, the total force experienced by the charged particle will be given by
\vec{F}={{\vec{F}}_{e}}+{{\vec{F}}_{m}}=q\vec{E}+q(\vec{v}\times \vec{B})
=q(\vec{E}+\vec{v}\times \vec{B})
This is called Lorentz force.
Motion of a charged particle in a Uniform Magnetic Field
Case-1
Consider the motion of a positively charged particle moving with an initial velocity \vec{v}perpendicular to a uniform magnetic field \vec{B} as shown in figure given below.
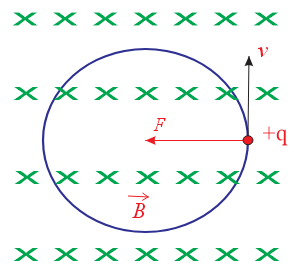
Since \vec{v} and \vec{B} are perpendicular, the particle experiences a force F = qvB of constant magnitude directed perpendicular to \vec{v}. Under the action of such a force the particle moves in a circular path with constant speed. The magnetic force provides the centripetal force. Applying Newton’s second law
qvB = \frac{{m{{v}^{2}}}}{r}
where r is the radius of the circular path.
r = \frac{{mv}}{{qB}}
The radius of the orbit is directly proportional to the linear momentum of the particle and inversely proportional to the magnetic field strength.
The time period is given by
T = \frac{{2\pi r}}{v}=\frac{{2\pi m}}{{qB}}
Note that time period is independent of velocity. All particles with same charge to mass ratio (q/m), have the same period.
Case-2
Suppose a particle of mass m and charge q, entering a uniform magnetic field induction \vec{B} at O, with velocity \vec{v}, making an angle \theta with the direction of magnetic field acting in the plane of paper as shown in figure.
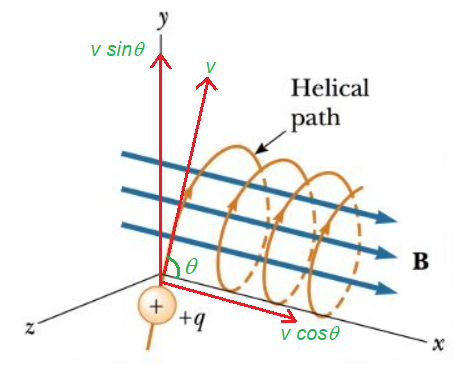
Resolving \vec{v} into two rectangular components we have:
v\cos \theta (={{v}_{1}}) acts in the direction of the magnetic field and v\sin \theta (={{v}_{2}}) acts perpendicular to the direction of magnetic field.
For component velocity {{\vec{v}}_{2}}, the force acting on the charged particle due to magnetic field is
\vec{F}=q({{\vec{v}}_{2}}\times \vec{B})
or F=q|{{\vec{v}}_{2}}\times \vec{B}|=q{{v}_{{2\,\,}}}B\,\sin 90{}^\circ
=q(v\sin \theta )\,B …(i)
The direction of this force \vec{F} is perpendicular to the plane containing \vec{B}and {{\vec{v}}_{2}} and hence acts perpendicular to the plane of the paper. As this force is to remain always perpendicular to {{\vec{v}}_{2}}, it can not change the magnitude of velocity {{\vec{v}}_{2}}. It changes only the direction of motion. Hence the charged particle is made to move on a circular path in the magnetic field, as shown in figure with dotted circle. The force F on the charged particle due to magnetic field provides the required centripetal force (=mv_{2}^{2}/r) necessary for motion along the circular path of radius.
\therefore B\,q\,{{v}_{2}}=mv_{2}^{2}/r
or {{v}_{2}}=B\,qr/m
or v\sin \theta =Bqr/m …(ii)
The angular velocity of rotation of the particle in magnetic field will be
\omega =\frac{{v\sin \theta }}{r}=\frac{{B\,qr}}{{mr}}=\frac{{B\,q}}{m}
The frequency of rotation of the particle in magnetic field will be
v=\frac{\omega }{{2\pi }}=\frac{{B\,q}}{{2\pi \,m}} …(iii)
The time period of revolution of the particle in the magnetic field will be
T=\frac{1}{v}=\frac{{2\pi \,m}}{{B\,q}} …(iv)
From (iii) and (iv) we note that and T do not depend upon velocity \vec{v} of the particle. It means, all the charged particles having the same specific charge (charge/mass) but moving with different velocities at a point, will complete their circular paths in the same time.
For component velocity {{v}_{1}}=(v\,\cos \,\theta ), there will be no force on the charged particle in the magnetic field, because, the angle between {{\vec{v}}_{1}} and \vec{B} is zero. Thus the charged particle covers the linear distance in direction of the magnetic field with a constant speed v\cos \theta .
Therefore, under the combined effect of the two component velocities, the charged particle in magnetic field will move on a circular pathe as well as it cover linear distance along the magnetic field so the resultant path of the charged particle will be helical in shape and is called Halix whose axis is parallel to the direction of magnetic field.
The linear distance covered by the charge particle in the magnetic field in time equal to one revolution of its circular path is known as pitch of helix.
Hence Pitch `d’ can be calculated as follows
d={{v}_{1}}T=v\,\,\cos \theta \,\,\frac{{2\pi m}}{{Bq}}.
Points to be Noted
(a) If a charged particle having charge is at rest on a magnetic field \vec{B}, it experiences no force, as v=0 and F=q\,v\,B\sin \theta
(b) If charged particle is moving parallel to the direction of \vec{B}, it also does not experience any force because angle \theta between \vec{v} and \vec{B} is \displaystyle {{0}^{o}}or{{180}^{o}}
because \sin 0{}^\circ =\sin 180{}^\circ =0. Therefore, the charged particle in this situation will continue moving along the same path with the same velocity.
(c) if charged particle is moving perpendicular to the direction of \vec{B}, it experiences a maximum force which acts perpendicular to the direction of \vec{B} as well as \vec{v} . Hence this force will provide the required centripetal force and the charged particle will describe a circular path in the magnetic field to radius , given by \frac{{m{{v}^{2}}}}{r}=Bq\,v
When a charged a particle is projected perpendicular to the magnetic field, (i) its path is circular in a plane perpendicular to the plane of magnetic field and direction of motion of the charged particle. (ii) the speed and kinetic energy of the particle remain constant. (iii) The velocity of the charged particle changes only in direction.
Work done by a Magnetic Force is zero.
Since \vec{F} is always perpendicular to \vec{v} there is no component of acceleration in the direction of velocity vector, therefore, magnitude of the velocity does not change, thus kinetic energy of the charge does not change, hence no work is done by the magnetic force.
Illustration : An electron with a kinetic energy of 103 eV moves perpendicular to the direction of uniform field B = 10–4 T. (a) What is the period of its orbit ? (b) What is the radius of its orbit ? Solution(a) Using equation of Time period T = \frac{{2\pi m}}{{eB}}=\frac{{2\pi (9.1\times {{{10}}^{{-31}}}\ kg)}}{{(1.6\times {{{10}}^{{-19}}}C)\ ({{{10}}^{{-4}}}T)}} or T = 3.6 ´ 10-7s (b) Using equation of the radius of the orbit r = \frac{{mv}}{{eB}}=\frac{p}{{eB}} , where p is the momentum The momentum of the electron can be obtained from kinetic energy as mv = \sqrt{{2Km}}=\sqrt{{2(1.6\times {{{10}}^{{-16}}}J)\ (9.1\times {{{10}}^{{-31}}}kg)}}= 1.7 ´ 10–23 kg m/s Thus, radius of the orbit is given by r = \frac{{(1.7\times {{{10}}^{{-23}}}\ kg\ m/s)}}{{(1.6\ \times \ {{{10}}^{{-19}}}C)\ ({{{10}}^{{-4}}}T)}} = 1.07 m
|
Illustration
An electron moving at 4 x 106 m/s enters a uniform field B = 0.04 T at \displaystyle {{30}^{o}} to the magnetic field lines. What is the pitch of the helical path.
Solution
\displaystyle {{v}_{\parallel }}=v.\cos \theta where v = 4 x 106 m/s ; \theta ={{30}^{o}}
\displaystyle \therefore {{v}_{{||}}}=\text{ }(4\times {{10}^{6}})\text{ }cos30{}^\circ \text{ }=\text{ }3.46\times {{10}^{6}}m/s Using equation
p = \frac{{2\pi m{{v}_{{||}}}}}{{qB}}
or p = 2 \pi \frac{{(9.1\ \times {{{10}}^{{-31}}})\ (3.46\times {{{10}}^{6}})}}{{(1.6\times {{{10}}^{{-19}}})\ (0.04)}} = 3.1 mm
Illustration
A beam of charged particles of K.E. = 1 keV and q = 1.6 ´ 10–19 C and two
masses 8 ´ 10–22 kg and 16 ´ 10–27 kg come out of an accelerator tube.
And strike a plate at distance of 1 cm from the end of the tube, from where
the particles emerge perpendicularly. The value of the smallest magnetic
field which can prevent the beam from striking the plate is
(1) 1.414 T (2) 2.828 T (3) 4.242 T (4) 5.656 T
Solution:
\vec{B} should be out of the paper. Let F be the magnetic force acting on the particles, where F = (mv2/r) = qvB since v is perpendicular to B. This force does not change the velocity of the particles but it bends them into a circular arc of radius r, where r = \left( {\frac{{mv}}{{qB}}} \right). The beam will not strike the plate,if the radius of path of the beam is at the most 1cm. So minimum magnetic field required is given by the equation of the radius Hence {{r}_{{\max }}}=\ \left( {\frac{{mv}}{{q{{B}_{{\min }}}}}} \right).
Bmin = \frac{{mv}}{{q\ \times \ {{{10}}^{{-2}}}}}\ =\ \frac{{mv}}{{(1.6\ \times \ {{{10}}^{{-19}}}\ \times \ {{{10}}^{{-2}}})}}
Now \frac{1}{2}\ m{{v}^{2}} = K.E. = 1.0 keV = 103 eV = 103 ´ 1.6 ´10–19 J
or v = (2 ´ 103 ´ 1.6 ´ 10-19 J/m)1/2 .
Bmin = \frac{{m\ \times \ {{{\left( {\frac{{2\ \times \ {{{10}}^{3}}\ \times \ 1.6\ \times \ {{{10}}^{{-19}}}}}{m}} \right)}}^{{1/2}}}}}{{1.6\ \times \ {{{10}}^{{-19}}}\times \ {{{10}}^{{-2}}}}}
= \sqrt{m}\ \sqrt{{\frac{{2\ \times \ {{{10}}^{3}}\times \ 1.6\ \times \ {{{10}}^{{-19}}}}}{{{{{(1.6\ \times \ {{{10}}^{{-21}}})}}^{2}}}}}}\ =\ \sqrt{m}\ {{\left[ {\frac{{3.2\ \times \ {{{10}}^{{-16}}}}}{{2.56\ \times \ {{{10}}^{{-42}}}}}} \right]}^{{1/2}}}
= \sqrt{m}\ \times \ {{(1.25\ \times \ {{10}^{{26}}})}^{{1/2}}}=\ \sqrt{m}\ \times \ 1.1\ \times \ {{10}^{{13}}}
Hence, Bmin is more if m is more. The higher masses can be prevented from striking the plate, if
Bmin =\ \sqrt{{16\ \times \ {{{10}}^{{-27}}}}}\ \sqrt{{1.25}}\ \times \ {{10}^{{13}}}
= (\sqrt{{1.6\ \times \ 1.25)}}\ =\ (\sqrt{2}) T = 1.414 T
Hence option (1) is correct
Objective Assignment
Q.1
A charged particle moves through a magnetic field. The effect of the field is to change the particle’s
(a) speed (b) direction of motion (c) energy (d) acceleration
Ans : (b)
Q.2
A charged particle is moved along a magnetic field line. The force on the particle is
(a) along its velocity
(b) opposite to its velocity
(c) perpendicular to its velocity
(d) zero
Ans : (d)
Q.3
Electrons moving with a constant velocity enter a uniform magnetic field B in a direction perpendicular to B. The electron path in the field is
(a) a helix
(b) a straight line parallel to B
(c) a straight line perpendicular to B
(d) a circle
Ans : (d)
Q.4
A beam of ions with velocity 2 ´ 105 m/s enter normally into a uniform magnetic field of
4 ´ 10-2 T. If the specific charge of the ions is 5 ´ 107 C/kg, the radius of the circular path described will be
(a) 0.10 m (b) 0.16 m (c) 0.20 m (d) 0.25 m
Ans : (a)
Q.5
If electron velocity is \left( {2\hat{i}+3\hat{j}} \right) and it is subjected to a magnetic field , then:
(a) speed will change
(b) path will change
(c) both (a) and (b)
(d) none of the above
Ans : (b)
Q.6
Two particles x and y having equal charges after being accelerated through the same p.d. enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of x and y is
(a) (R1/R2)1/2 (b) (R2/R1) (c) (R1/R2)2 (d) (R1/R2)
Ans : (c)
Q.7
An electron is moving in a circle of radius r in a uniform magnetic field B. Suddenly the field is reduced to B/2. The radius of the circle now becomes.
(a) r/2 (b) r/4 (c) 2r (d) 4r
Ans : (c)
Q.8
A positively charged particle moving with velocity enters a region of space having a constant magnetic induction . The particle will experience the largest force when the angle between vectors and is :
(a) 0° (b) 45° (c) 90° (d) 180°
Ans : (c)
Q.9
An electron accelerated through a potential difference V passes through a uniform transverse magnetic field and experiences a force F. If the accelerating potential is increased to 2V, the electrons in the same magnetic field will experience a force
(a) \sqrt{2}F
(b) 2F
(c) 2\sqrt{2}F
(d) 4F
Ans. (a)
Q.10
A charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
(a) \displaystyle \sqrt{{\frac{{Vm}}{{q{{B}^{2}}}}}}
(b) \displaystyle \frac{{2Vm}}{{q{{B}^{2}}}}
(c) \displaystyle \sqrt{{\frac{{2Vm}}{q}}}\left( {\frac{1}{B}} \right)
(d) \displaystyle \sqrt{{\frac{{Vm}}{q}}}\left( {\frac{1}{B}} \right)
Ans. (c)
Q.11
The acceleration of an electron at a certain moment in a magnetic field B=2\hat{i}+3\hat{j}+4\hat{k} is a=x\,\,\hat{i}+\hat{j}-\hat{k}. The value of x is
(a) 0.5 (b) 1 (c) 2.5 (d) 1.5
Ans. (a)
Q.12
Two charged particles P and Q enter a uniform magnetic field normally with the same speed. Their paths in the field are as shown in the figure. It can be concluded that
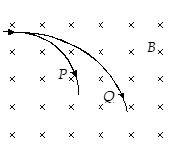
(a) the charge of P is greater than that of Q
(b) the specific charge of P is greater than that of Q
(c) both P and Q are positively charged
(d) both P and Q have same mass
Ans. (b)
13.
A long straight wire carries a current of 20 A. An electron at a distance of 10 cm from it is moving with a velocity of {{10}^{6}}\,\,m{{s}^{{-1}}}. What is the force on the electron when
(i)
it is moving parallel to the wire
(a) 6.4\times {{10}^{{-18}}}\,\,N
(b) 6.4\times {{10}^{{18}}}\,\,N
(c) 6.4\times {{5}^{{18}}}\,\,N
(d) 6.4\times {{5}^{{-18}}}\,\,N
Ans (b)
(ii)
it is moving towards the wire and
(a) 6.4\times {{10}^{{-18}}}\,\,N
(b) 6.4\times {{10}^{{18}}}\,\,N
(c) 6.4\times {{5}^{{18}}}\,\,N
(d) 6.4\times {{5}^{{-18}}}\,\,N
Ans (a)
(iii)
it is moving perpendicular to the above two directions?
(a)zero
(b)5
(c)3
(d)2
Ans (a)
14.
A 10\,eVelectron is circulating in a plane at right angles to a uniform field of a magnetic induction of {{10}^{{-4}}}\,\,\mathbf{Tesla}. What is the radius of its orbit?
(a)0.1 m
(b)0.11 m
(c)0.21 m
(d)0.30 m
Ans (b)
15.
A rectangular lop of side a = 25 cm and b = 10 cm carrying a current I=15\,\,A is placed with its longer side parallel to a long conductor d = 2.0 cm apart carrying a current I’=25\,\,A. What is the net force on the loop?
(a) 7.8\times {{10}^{{-5}}}\,\,N
(b) 7.5\times {{10}^{{-5}}}\,\,N
(c) 7.0\times {{10}^{{-5}}}\,\,N
(d) 8.5\times {{10}^{{-5}}}\,\,N
Ans (a)
16.
A flat silver strip of width 2.0 cm and thickness 1.0 mm carries a current to 10 A. A magnetic field of 0.2 T is applied perpendicular to the flat face of the strip. The emf developed across the width of the strip is measured to be 2\mu V. Find the density of free electrons in the metal.
(a) 6.5\times {{10}^{{28}}}
(b) 6.25\times {{10}^{{28}}}
(c) 6.00\times {{10}^{{28}}}
(d) 6.25\times {{10}^{{-28}}}
Ans (b)
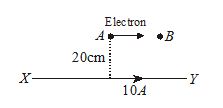
17.
An infinite long straight conductor XY is carrying a current of 10A. An electron is moving with a speed of parallel to the conductor in air from point A to B, as shown in figure. The perpendicular distance between the electron and the conductor XY is 20 cm. Calculate the magnitude of the force experienced by the electron. Write the direction of this force
(a) 1.6\times {{5}^{{19}}}\,N
(b) 1.6\times {{5}^{{-19}}}\,N
(c) 1.6\times {{10}^{{-19}}}\,N
(d) 1.6\times {{10}^{{19}}}\,N
Ans (c)
18.
A proton and an \alpha -particle enter a uniform magnetic field at right angles to it with same velocity. Find the ratio of time period of revolution \alpha -particle and the proton.
(a)2 : 5
(b)2 : 3
(c)2 : 1
(d)1 : 3
Ans (c)
19.
A beam of charged particles having kinetic energy and containing masses 8\times {{10}^{{-27}}}\,kgand 1.6\times {{10}^{{-26}}}\,kg, emerges from the end of an accelerated tube. There is a plate at a distance \displaystyle {{10}^{{-2}}}m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plane.
(a) \frac{{\sqrt{5}}}{q}\times 1.6\times {{10}^{{-19}}}T
(b) \frac{{\sqrt{2}}}{q}\times 2\times {{10}^{{-20}}}T
(c) \frac{{\sqrt{2}}}{q}\times 1.6\times {{10}^{{-19}}}T
(d) \frac{{\sqrt{2}}}{q}\times 1.6\times {{10}^{{19}}}T
Ans (c)
20.
An electron beam passes through a magnetic field of 2\times {{10}^{{-3}}}\mathbf{weber/}{{\mathbf{m}}^{\mathbf{2}}} and an electric field of 1.0\times {{10}^{4}}\,\,V{{m}^{{-1}}}both acting simultaneously. The path of electrons remaining undeviated, calculate the speed of the electrons. If the electric field is removed what will be the radius of the electron path?
(a) 5\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
(b) 3\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
(c) 5\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
(d) 5\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
Ans (a)
Subjective Assignment
Q.1
What is the magnitude of force on a charge q moving with a velocity V in a magnetic field B ?
Q.2.
The force F experienced by a particle of charge q moving with velocity v in a magnetic field B is given by F = q (v x B). Which pair of vectors are always mutually perpendicular?
Q.3.
Under what condition is the force acting on a charge moving through a uniform magnetic field minimum ?
Q.4.
An electron beam is moving vertically upwards. In a magnetic field which is from south to north in a horizontal plane, Find direction of deflected.
Q.5.
In a certain arrangement a proton does not get deflected while passing through a magnetic field region. Under what condition is it possible ‘?
Q.6.
An electron and a proton moving with the same speed enter the same magnetic field region at right angles to the direction of the field. For which of the two particles will the radius of circular path be smaller
Q.7.
A beam of alpha particles and of the protons of’ the same velocity v, enter a uniform magnetic field at right angles to the field lines. The particles describe circular paths. What is the ratio of the radii of these two particles’? [Ans. 2:11 ]
Q.8
What are Aurora Borielies light. Where do they occur mostly in the world and why ?
Q.9
If you are in southern hemisphere of earth and an electron is seen to fly from east then what is the direction of its deflection due to earth’s magnetic field if you are facing east ?
Q.10.
Is any work done by a magnetic field on a moving charge ‘?Why ‘?
Q.11.
A proton & an a-particle of the same K.E, in turn move through a uniform magnetic field B, in a plane normal to the field. Compare the radii of the paths of the two particle.
Q.12
An electron is moving with a speed of 106m/s. It enter into a magnetic field of 100gauss with its velocity perpendicular to the field. Find the radius of its trajectory and its frequency of rotation.
Q.13
An electron emitted by a heated cathode and accelerated through a potential difference of 2kV , enter a region with uniform magnetic field of 0.15T.Determine the trajectory of the electron if the field is
(a) transverse to the initial velocity
(b) parallel to the initial
(c) making an angle of 30o with the initial velocity.
Q.14
A cyclotron has two dees each of radius 0.5m and placed in a magnetic field of 0.2T applied perpendicular to the plane of dees.Find the maximum kinetic energy of the alpha particle which has been accelerated through it in eV. Also find the frequency of the oscillator required.
Q.15
In a cyclotron neon ions are accelerated to an energy of
100 MeV. The diameter of the dees is 310 cm, the magnetic field induction in the gap is 1.1 T, the acceleration potential is 300 kV. Find the degree of ionization of a neon atom, the total number of revolutions of an ion in the process of its acceleration and the frequency of the change in polarity of the accelerating field.
Q.16
An electron beam is accelerated through a potential difference of 2kV. And then it is allowed to enter into a magnetic field of 50G. If the electron beam was moving in x-z plane and the magnetic field is transverse to its direction in the same plane then find the deflection in the beam over a distance of 50cm.
Q.17
A beam of alpha particals is moving with a speed of 2000 m/sec when it enter a magnetic field of 0.05T at an angle of 60o as shown in the diagram. Find the radius, pitch , and frequency of its rotation.
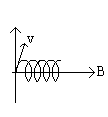
Q.18
An electron beam passes through a magnetic field of 2mT and an electric field of 3400volts/m both acting simultaneously. If the path of the electron remains un-deviated, calculate the speed of the electron. If the electric field is removed, what will be the radius of the path?
Q.19
An alpha- particle moves in a uniform magnetic field with an induction of 1.2 tesla (T) in a circle of 49 cm radius in the plane perpendicular to the lines of force. Find the speed and the kinetic energy of the particle.
Q.20
A beam of protons with velocity of 4 x 105 m/sec, enters a uniform magnetic field of 0.3 tesla at an angle of 600 with ate magnetic field. Find the radius of the helical path taken by the proton beam. Also find the pitch of the helix. Mass of proton = 1.67 x 10 -27 kg.
Q.21
A wire of radius R carries a steady current I and electron escapes with a velocity v perpendicular to the surface of the wire. Find the distance traveled by the electron before its velocity becomes zero.
Q.22
Two electrons move parallel to each other with the same velocity of 3 x 10 6 m/s. Find the ratio of the magnetic and electrostatic forces of interaction between the two.
Q.23
A proton beam in an acceleration moves at a speed of 0.990 c relative to the accelerator. Compare the force of interaction between the protons with the Coulomb force.
Q.24.
An electron of kinetic energy 25 keV moves perpendicular to the direction of a uniform magnetic field of 0.2 milli tesla. Calculate the time period of rotation of the electron in the magnetic field. [Ans. l.79xl0-7s]
Q.25.
An electron in an atom revolves around the nucleus in an orbit of radius 0.53 Ao. Calculate the equivalent magnetic moment if the frequency of revolution of electron is 6.8 x 109MHz.
[Ans. 9.6×10-24Am2]
Q.26.
An electron moving with a speed of 108 rn/s enters a magnetic field of 5xl0-3T in a direction perpendicular to the field. Calculate
(a)radius of path
(b) frequency of revolution of electron.
Q.27.
An electron being accelerated through 100V enters a uniform magnetic field of 0.004T perpendicular to direction of motion. Calculate the radius of path followed by electron.
Q.28.
An electron travels in a circular path of radius 20 cm in a magnetic field of 2 x l0-3 T.Calculate the speed of the electron. What is the potential difference through which the electron must be accelerated to acquire this speed ?
[Ans. 7.04×107ms’7]
Case-2
Suppose a particle of mass m and charge q, entering a uniform magnetic field induction \vec{B} at O, with velocity \vec{v}, making an angle \theta with the direction of magnetic field acting in the plane of paper as shown in figure.

Resolving \vec{v} into two rectangular components we have:
v\cos \theta (={{v}_{1}}) acts in the direction of the magnetic field and v\sin \theta (={{v}_{2}}) acts perpendicular to the direction of magnetic field.
For component velocity {{\vec{v}}_{2}}, the force acting on the charged particle due to magnetic field is
\vec{F}=q({{\vec{v}}_{2}}\times \vec{B})
or F=q|{{\vec{v}}_{2}}\times \vec{B}|=q{{v}_{{2\,\,}}}B\,\sin 90{}^\circ
=q(v\sin \theta )\,B …(i)
The direction of this force \vec{F} is perpendicular to the plane containing \vec{B}and {{\vec{v}}_{2}} and hence acts perpendicular to the plane of the paper. As this force is to remain always perpendicular to {{\vec{v}}_{2}}, it can not change the magnitude of velocity {{\vec{v}}_{2}}. It changes only the direction of motion. Hence the charged particle is made to move on a circular path in the magnetic field, as shown in figure with dotted circle. The force F on the charged particle due to magnetic field provides the required centripetal force (=mv_{2}^{2}/r) necessary for motion along the circular path of radius.
\therefore B\,q\,{{v}_{2}}=mv_{2}^{2}/r
or {{v}_{2}}=B\,qr/m
or v\sin \theta =Bqr/m …(ii)
The angular velocity of rotation of the particle in magnetic field will be
\omega =\frac{{v\sin \theta }}{r}=\frac{{B\,qr}}{{mr}}=\frac{{B\,q}}{m}
The frequency of rotation of the particle in magnetic field will be
v=\frac{\omega }{{2\pi }}=\frac{{B\,q}}{{2\pi \,m}} …(iii)
The time period of revolution of the particle in the magnetic field will be
T=\frac{1}{v}=\frac{{2\pi \,m}}{{B\,q}} …(iv)
From (iii) and (iv) we note that and T do not depend upon velocity \vec{v} of the particle. It means, all the charged particles having the same specific charge (charge/mass) but moving with different velocities at a point, will complete their circular paths in the same time.
For component velocity {{v}_{1}}=(v\,\cos \,\theta ), there will be no force on the charged particle in the magnetic field, because, the angle between {{\vec{v}}_{1}} and \vec{B} is zero. Thus the charged particle covers the linear distance in direction of the magnetic field with a constant speed v\cos \theta .
Therefore, under the combined effect of the two component velocities, the charged particle in magnetic field will move on a circular pathe as well as it cover linear distance along the magnetic field so the resultant path of the charged particle will be helical in shape and is called Halix whose axis is parallel to the direction of magnetic field.
The linear distance covered by the charge particle in the magnetic field in time equal to one revolution of its circular path is known as pitch of helix.
Hence Pitch `d’ can be calculated as follows
d={{v}_{1}}T=v\,\,\cos \theta \,\,\frac{{2\pi m}}{{Bq}}.
Note:
(a) If a charged particle having charge is at rest on a magnetic field \vec{B}, it experiences no force, as v=0 and F=q\,v\,B\sin \theta
(b) If charged particle is moving parallel to the direction of \vec{B}, it also does not experience any force because angle \theta between \vec{v} and \vec{B} is \displaystyle {{0}^{o}}or{{180}^{o}}
because \sin 0{}^\circ =\sin 180{}^\circ =0. Therefore, the charged particle in this situation will continue moving along the same path with the same velocity.
(c) if charged particle is moving perpendicular to the direction of \vec{B}, it experiences a maximum force which acts perpendicular to the direction of \vec{B} as well as . Hence this force will provide the required centripetal force and the charged particle will describe a circular path in the magnetic field to radius , given by \frac{{m{{v}^{2}}}}{r}=Bq\,v
When a charged a particle is projected perpendicular to the magnetic field, (i) its path is circular in a plane perpendicular to the plane of magnetic field and direction of motion of the charged particle. (ii) the speed and kinetic energy of the particle remain constant. (iii) The velocity of the charged particle changes only in direction. The force acting on the charged particle is independent of the radius of circular path but depends upon the speed of the charged particle i.e., F\propto \,r{}^\circ (but F\propto \,v). (v) The time period of revolution of a charged particle in the magnetic field is independent of velocity of particle and radius of the circular path i.e., T\,\propto \,\,{{r}^{o}}\,{{v}^{o}}.
