Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Basic Level)
Q.1
The resistance of a wire is 10W. Its length is increased by 10% by stretching. The new resistance will now be nearly
(a) 12 W (b) 1.2 W (c) 13 W (d) 11 W
Ans : (a)
Q.2
The same mass of copper is drawn into two wires 1 mm and 2 mm thick. Two wires are connected in series and current is passed through them. Heat produced in the wire is in the ratio
(a) 2 : 1 (b) 1 : 16 (c) 4 : 1 (d) 16 : 1
Ans : (d)
Practice Questions (JEE Main Level)
Q.1
The figure shows two squares, X and Y, cut from a sheet of metal of uniform thickness t. X and Y have sides of length L and 2L, respectively.
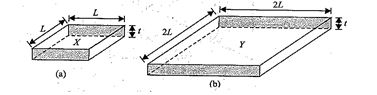
The resistances \displaystyle {{R}_{x}} and \displaystyle {{R}_{y}} of the squares are measured between the opposite faces shaded in fig. What is the value of \displaystyle {{R}_{x}}/{{R}_{y}}?
(a) 1/4
(b) 1/2
(c) 1
(d) 2
Ans. (c)
Q.2
The plot represents the flow of current through a wire at three different times. The ratio of charges flowing through the wire at different times is
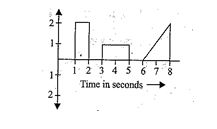
(a) 2 : 1 : 2
(b) 1 : 3 : 3
(c) 1 : 1 : 1
(d) 2 : 3 : 4
Ans. (c)
Q.3
Resistance of a resistor at temperature tºC is \displaystyle {{R}_{t}}={{R}_{0}}\left( {1+\alpha t+\beta {{t}^{2}}} \right), where \displaystyle {{R}_{0}} is the resistance at 0ºC. The temperature coefficient of resistance at temperature tºC is
(a) \displaystyle \frac{{\left( {1+\alpha t+\beta {{t}^{2}}} \right)}}{{\alpha +2\beta t}}
(b) \displaystyle \left( {\alpha \,+\,2\beta t} \right)
(c) \displaystyle \frac{{\alpha \,+\,2\beta t}}{{\left( {1+\alpha t+\beta {{t}^{2}}} \right)}}
(d) \displaystyle \frac{{\alpha \,+\,2\beta t}}{{2\left( {1+\alpha t+\beta {{t}^{2}}} \right)}}
Ans. (c)
Q.4
The masses of the three wire of copper are in the ratio 1 : 3 : 5. And their lengths are in the ratio 5 : 3 : 1. The ratio of their electrical resistance is
(a) 1 : 3 : 5
(b) 5 : 3 : 1
(c) 1 ; 15 : 125
(d) 125 : 15 : 1
Ans. (d)
Q.5
For a cell, a graph is plotted between the potential difference V across the terminals of the cell and the current I drawn from the cell (see in fig.) the emf and the internal resistance of the cell are E and r, respectively. Then
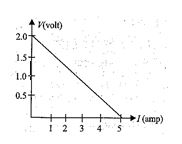
(a) \displaystyle E\,=\,2V,\,\,r\,=\,0.5\,\Omega
(b) \displaystyle E\,=\,2V,\,\,r\,=\,0.4\,\Omega
(c) \displaystyle E\,>\,2V,\,\,r\,=\,0.5\,\Omega
(d) \displaystyle E\,>\,2V,\,\,r\,=\,0.4\,\Omega
Ans. (b)
Q.6
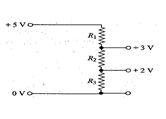
A potential divider is used to give outputs of 2V and 3V from a 5V source, as shown in fig. Which combination of resistances \displaystyle {{R}_{1}}, \displaystyle {{R}_{2}}and \displaystyle {{R}_{3}} gives the correct voltages ?
\displaystyle {{R}_{1}}k\Omega | \displaystyle {{R}_{2}}k\Omega | A \displaystyle {{R}_{3}}k\Omega | |
(a) | 1 | 1 | 2 |
(b) | 2 | 1 | 2 |
(c) | 3 | 2 | 2 |
(d) | 3 | 2 | 3 |
Ans. (b)
Q.7
The temperature coefficient of resistance of conductor varies as \displaystyle \alpha \left( T \right)\,=\,3{{T}^{2}}+2T. If \displaystyle {{R}_{0}} is resistance at T = 0 and R is resistance at T, then
(a) \displaystyle R\,=\,{{R}_{0}}\left( {6T+2} \right)
(b) \displaystyle R\,=\,{{2}_{0}}\left( {3+2T} \right)
(c) \displaystyle R\,=\,{{R}_{0}}\left( {1+{{T}^{2}}+{{T}^{3}}} \right)
(d) \displaystyle R\,=\,{{R}_{0}}\left( {1-T+{{T}^{2}}+{{T}^{3}}} \right)
Ans. (c)
Q.8
A battery of emf E and internal resistance r is connected across a resistance R. Resistance R can be adjusted to any value greater than or equal to zero. A graph is plotted between the current passing through the resistance (I) and potential difference (V) across It. Select the correct alternatives.
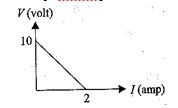
(a) Internal resistance of the battery is 5 \displaystyle \Omega
(b) Emf of the battery is 10 V
(c) Maximum current that can be taken from the battery is 2A.
(d) Al the above
Ans. (d)
Q.9
A conductor of resistivity \displaystyle \rho and resistance R, as shown in the figure, is connected across a battery of emf V. Its radius varies from a at left end to b at right end. The electric field at a point P at distance x from left end of it is
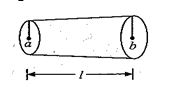
(a) \displaystyle \frac{{2V{{l}^{2}}\rho }}{{\pi R{{{\left[ {la+\left( {b-a} \right)x} \right]}}^{2}}}}
(b) \displaystyle \frac{{V{{l}^{2}}\rho }}{{\pi R{{{\left[ {la+\left( {b-a} \right)x} \right]}}^{2}}}}
(c) \displaystyle \frac{{V{{l}^{2}}\rho }}{{2\pi R{{{\left( {la+\left( {b-a} \right)x} \right)}}^{2}}}}
(d) none of these
Ans. (b)
Q.10
Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
(a) \displaystyle \frac{{4\pi \sigma }}{{\ell b\left( {b/a} \right)}}
(b) \displaystyle \frac{{4\pi \sigma }}{{\left( {b/a} \right)}}V
(c) \displaystyle \frac{{2\pi \sigma }}{{\ell n\left( {b/a} \right)}}V
(d) \displaystyle \frac{{2\pi \sigma }}{{\left( {b+a} \right)}}V
Ans. (c)
Q.11
A cylindrical tube of length l has an inner radius a and an outer radius b. The resistivity is . What is the resistance between the ends?
(a) \displaystyle R=\frac{{\rho l}}{{\pi ({{b}^{2}}-{{a}^{2}})}}
(b) R=\frac{{\rho l}}{{{{\pi }^{2}}(b-a)}}
(c) R=\frac{{2\rho l}}{{3{{\pi }^{2}}(2b-a)}}
(d) none
Ans. (a)
Q.12
A cylindrical rod of silicon has a length of 1 cm and a radius of 2mm. What is the current when a potential difference of 120V is applied across the ends? (Take SI = 2200m).
(a)1.345 mA (b) 6.85 × 10–5A (c)645mA (d) none
Ans. (b)
Q.13
The resistance of a copper wire is 0.8 \displaystyle \Omega at 20°C. When it is placed in an oven, its resistance is 1.2. What is the temperature of the oven? Thermal coefficient of resistance of copper is \displaystyle {{\alpha }_{{Cu}}}= 3.9 × 10–3/°C
(a) 134°C (b) 214°C (c)178°C (d) 128°C
Ans. (d)
Practice Questions (JEE Advance Level)
1.
A cylindrical conductor AB of length l and area of cross-section a is connected to a battery having emfE and negligible internal resistance. The specific conductivity of cylindrical conductor varies as \sigma ={{\sigma }_{0}}\frac{l}{{\sqrt{x}}}, where s0 is constant and x is distance from end A. What is the electric field just near the end B of cylinder?
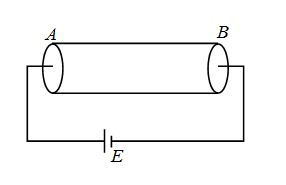
(a) \frac{E}{l}
(b) \frac{{3\,E}}{{2\,l}}
(c) \frac{{2\,E}}{{3\,l}}
(d) \frac{E}{{2\,l}}
Ans (b)
