Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-1)
Q.1
The resistance of a wire is 10W. Its length is increased by 10% by stretching. The new resistance will now be nearly
(a) 12 W
(b) 1.2 W
(c) 13 W
(d) 11 W
Ans : (a)
Q.2
The same mass of copper is drawn into two wires 1 mm and 2 mm thick. Two wires are connected in series and current is passed through them. Heat produced in the wire is in the ratio
(a) 2 : 1
(b) 1 : 16
(c) 4 : 1
(d) 16 : 1
Ans : (d)
Practice Questions (Level-2)
Q.1
The figure shows two squares, X and Y, cut from a sheet of metal of uniform thickness t. X and Y have sides of length L and 2L, respectively.
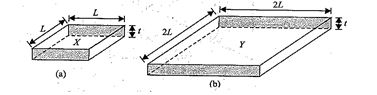
The resistances \displaystyle {{R}_{x}} and \displaystyle {{R}_{y}} of the squares are measured between the opposite faces shaded in fig. What is the value of \displaystyle {{R}_{x}}/{{R}_{y}}?
(a) 1/4
(b)1/2
(c) 1
(d) 2
Ans. (c)
Q.2
The plot represents the flow of current through a wire at three different times. The ratio of charges flowing through the wire at different times is
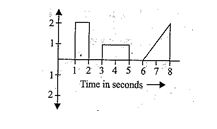
(a) 2 : 1 : 2
(b) 1 : 3 : 3
(c) 1 : 1 : 1
(d) 2 : 3 : 4
Ans. (c)
Q.3
Resistance of a resistor at temperature tºC is \displaystyle {{R}_{t}}={{R}_{0}}\left( {1+\alpha t+\beta {{t}^{2}}} \right), where \displaystyle {{R}_{0}} is the resistance at 0ºC. The temperature coefficient of resistance at temperature tºC is
(a) \displaystyle \frac{{\left( {1+\alpha t+\beta {{t}^{2}}} \right)}}{{\alpha +2\beta t}}
(b) \displaystyle \left( {\alpha \,+\,2\beta t} \right)
(c) \displaystyle \frac{{\alpha \,+\,2\beta t}}{{\left( {1+\alpha t+\beta {{t}^{2}}} \right)}}
(d) \displaystyle \frac{{\alpha \,+\,2\beta t}}{{2\left( {1+\alpha t+\beta {{t}^{2}}} \right)}}
Ans. (c)
Q.4
The masses of the three wire of copper are in the ratio 1 : 3 : 5. And their lengths are in the ratio 5 : 3 : 1. The ratio of their electrical resistance is
(a) 1 : 3 : 5
(b) 5 : 3 : 1
(c) 1 ; 15 : 125
(d) 125 : 15 : 1
Ans. (d)
Q.5
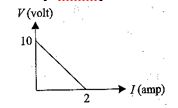
For a cell, a graph is plotted between the potential difference V across the terminals of the cell and the current I drawn from the cell (see in fig.) the emf and the internal resistance of the cell are E and r, respectively. Then
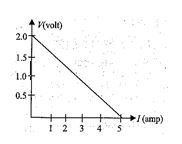
(a) \displaystyle E\,=\,2V,\,\,r\,=\,0.5\,\Omega
(b) \displaystyle E\,=\,2V,\,\,r\,=\,0.4\,\Omega
(c) \displaystyle E\,>\,2V,\,\,r\,=\,0.5\,\Omega
(d) \displaystyle E\,>\,2V,\,\,r\,=\,0.4\,\Omega
Ans. (b)
Q.6
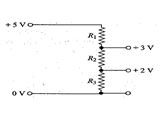
A potential divider is used to give outputs of 2V and 3V from a 5V source, as shown in fig. Which combination of resistances \displaystyle {{R}_{1}}, \displaystyle {{R}_{2}}and \displaystyle {{R}_{3}} gives the correct voltages ?
\displaystyle {{R}_{1}}k\Omega | \displaystyle {{R}_{2}}k\Omega | A \displaystyle {{R}_{3}}k\Omega | |
(a) | 1 | 1 | 2 |
(b) | 2 | 1 | 2 |
(c) | 3 | 2 | 2 |
(d) | 3 | 2 | 3 |
Ans. (b)
Q.7
The temperature coefficient of resistance of conductor varies as \displaystyle \alpha \left( T \right)\,=\,3{{T}^{2}}+2T. If \displaystyle {{R}_{0}} is resistance at T = 0 and R is resistance at T, then
(a) \displaystyle R\,=\,{{R}_{0}}\left( {6T+2} \right)
(b) \displaystyle R\,=\,{{2}_{0}}\left( {3+2T} \right)
(c) \displaystyle R\,=\,{{R}_{0}}\left( {1+{{T}^{2}}+{{T}^{3}}} \right)
(d) \displaystyle R\,=\,{{R}_{0}}\left( {1-T+{{T}^{2}}+{{T}^{3}}} \right)
Ans. (c)
Q.8
A battery of emf E and internal resistance r is connected across a resistance R. Resistance R can be adjusted to any value greater than or equal to zero. A graph is plotted between the current passing through the resistance (I) and potential difference (V) across It. Select the correct alternatives.
(a) Internal resistance of the battery is 5 \displaystyle \Omega
(b) Emf of the battery is 10 V
(c) Maximum current that can be taken from the battery is 2A.
(d) Al the above
Ans. (d)
Q.9
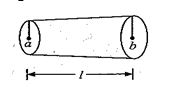
A conductor of resistivity \displaystyle \rho and resistance R, as shown in the figure, is connected across a battery of emf V. Its radius varies from a at left end to b at right end. The electric field at a point P at distance x from left end of it is
(a) \displaystyle \frac{{2V{{l}^{2}}\rho }}{{\pi R{{{\left[ {la+\left( {b-a} \right)x} \right]}}^{2}}}}
(b) \displaystyle \frac{{V{{l}^{2}}\rho }}{{\pi R{{{\left[ {la+\left( {b-a} \right)x} \right]}}^{2}}}}
(c) \displaystyle \frac{{V{{l}^{2}}\rho }}{{2\pi R{{{\left( {la+\left( {b-a} \right)x} \right)}}^{2}}}}
(d) none of these
Ans. (b)
Q.10
Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
(a) \displaystyle \frac{{4\pi \sigma }}{{\ell b\left( {b/a} \right)}}
(b) \displaystyle \frac{{4\pi \sigma }}{{\left( {b/a} \right)}}V
(c) \displaystyle \frac{{2\pi \sigma }}{{\ell n\left( {b/a} \right)}}V
(d) \displaystyle \frac{{2\pi \sigma }}{{\left( {b+a} \right)}}V
Ans. (c)
Q.11
A cylindrical tube of length l has an inner radius a and an outer radius b. The resistivity is . What is the resistance between the ends?
(a) \displaystyle R=\frac{{\rho l}}{{\pi ({{b}^{2}}-{{a}^{2}})}}
(b) R=\frac{{\rho l}}{{{{\pi }^{2}}(b-a)}}
(c) R=\frac{{2\rho l}}{{3{{\pi }^{2}}(2b-a)}}
(d) none
Ans. (a)
Q.12
A cylindrical rod of silicon has a length of 1 cm and a radius of 2mm. What is the current when a potential difference of 120V is applied across the ends? (Take SI = 2200m).
(a)1.345 mA (b) 6.85 × 10–5A (c)645mA (d) none
Ans. (b)
Q.13
The resistance of a copper wire is 0.8 \displaystyle \Omega at 20°C. When it is placed in an oven, its resistance is 1.2. What is the temperature of the oven? Thermal coefficient of resistance of copper is \displaystyle {{\alpha }_{{Cu}}}= 3.9 × 10–3/°C
(a) 134°C (b) 214°C (c)178°C (d) 128°C
Ans. (d)
