Video Lecture
Theory For Notes Making
Illustrations
Two electric charges q and -2q are placed at a distance 6 m apart on a horizontal plane. Find the locus of point on this plane where the potential has a value zero.
Solution
Let the charge q is placed at the origin (O) and -2q at (6m, 0m) in the xy-plane. Let the potential at P\,\left( {x,\,\,y} \right) is zero i.e.
\frac{{kq}}{{\sqrt{{{{x}^{2}}+{{y}^{2}}}}}}-\frac{{k\left( {2q} \right)}}{{\sqrt{{{{{(x-6)}}^{2}}+{{y}^{2}}}}}}=0
{{x}^{2}}+{{y}^{2}}=\frac{{{{{(x-6)}}^{2}}+{{y}^{2}}}}{4}
\displaystyle \Rightarrow \,\,{{x}^{2}}\,+\,{{y}^{2}}-4x\,\,=\,12 , \displaystyle {{x}^{2}}-4x+{{4}^{2}}=12+4
\displaystyle {{\left( {x-2} \right)}^{2}}+{{y}^{2}}={{4}^{2}}
After solving we get
Hence the locus of point in the x-y plane where the potential has zero value is a circle of radius 4 m and center (-2, 0) m.
Illustrations
\displaystyle E=20\hat{i}+30\hat{j} exists in space. If the potential at the origin is taken to be zero, find the potential at P (3, 2).
Solution
\displaystyle V={{V}_{x}}+{{v}_{y}}
\displaystyle =\int\limits_{0}^{3}{{-{{E}_{x}}dx}}+\int\limits_{0}^{2}{{-{{E}_{y}}dy}}
\displaystyle =\int\limits_{0}^{3}{{-20\,dx}}+\int\limits_{0}^{2}{{-30dx=-60-60=-120V}}
Ans. (d)
Illustration
Determine the potential energy of the assembly of charges, as shown in figure.
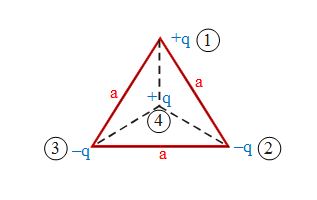
Solution
The potential energy of the assembly of charges is given by
\displaystyle U\,\,\,=\,\,\,\frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\,\,\sum\limits_{{i\,\ne \,j}}^{n}{{\frac{{{{q}_{i}}\,\,{{q}_{j}}}}{{{{r}_{{ij}}}}}}}
or \displaystyle U\,\,\,\,=\,\,({{U}_{{12}}}\,\,+\,\,{{U}_{{13}}}\,\,+\,\,{{U}_{{14}}})\,\,+\,\,({{U}_{{23}}}\,\,+\,\,{{U}_{{24}}})\,\,+\,\,{{U}_{{34}}}
or \displaystyle U\,\,=\,\,-\,\,\frac{{k\,\,{{q}^{2}}}}{a}\,\,=\,\,\frac{{-k{{q}^{2}}}}{a}\,\,+\,\,\frac{{k\,\,{{q}^{2}}}}{{a/\sqrt{3}}}\,\,+\,\,K\,\cdot \,\,\frac{{{{q}^{2}}}}{a}\,\,+\,\,\left( {\frac{{-k\,{{q}^{2}}}}{{a/\sqrt{3}}}} \right)\,\,\,+\,\,\,\left( {\frac{{-k\,\,{{q}^{2}}}}{{a/\sqrt{3}}}} \right)
(where \displaystyle k\,\,=\,\,\frac{1}{{4\pi \,{{\varepsilon }_{0}}}})
or \displaystyle U\,\,=\,\,\frac{{k\,{{q}^{2}}}}{a}\,\,\,\left( {\sqrt{3}+1} \right)\,\,=\,\,\,\,\frac{{{{q}^{2}}\left( {\sqrt{3}+1} \right)}}{{4\pi \,{{\varepsilon }_{0}}\,\,a}}
Illustration
Three point charges q1= 1 µC, q2 = -2µC and q3 = 3 µC are fixed at the positions shown in the figure
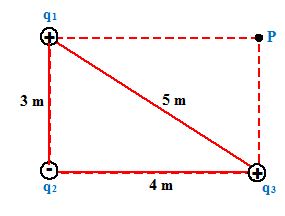
(a) What is the potential at point P at the corner of the rectangle ?
(b) How much work would be needed to bring a charge q4 = 2.5 µC from infinity and to place it at P ?
(c) What is the total potential energy of q1, q2 and q3 ?
Solution
(a)
The total potential at the point P is the scalar sum
VP = V1 + V2 + V3 = \frac{{k{{q}_{1}}}}{{{{r}_{1}}}}\,+\frac{{k{{q}_{2}}}}{{{{r}_{2}}}}\,+\frac{{k{{q}_{3}}}}{{{{r}_{3}}}}
Using the given values
V1 = \frac{{(9.0\,\,\times \,\,{{{10}}^{9}})\,\,({{{10}}^{{-6}}}C)}}{4}\,=2.25\,\,\times \,\,{{10}^{3}}\,V
Similarly, V2 = -3.6 x 103 V and V3 = 9 x 103 V
The total potential is VP = 7.65 x 103 V
(b)
The External work is Wext = q (Vf– Vi). In this case Vi = 0, so
Wext = q4VP = (2.5 x 10–6C) (7.65 x 103 V) = 0.19 J
(c)
The total potential energy of the three charges in the (scalar) sum
U = U12 + U13 + U23 = \frac{{k{{q}_{1}}{{q}_{2}}}}{{{{r}_{{12}}}}}\,+\frac{{k{{q}_{1}}{{q}_{3}}}}{{{{r}_{{13}}}}}\,+\frac{{k{{q}_{2}}{{q}_{3}}}}{{{{r}_{{23}}}}}
We find, for example
U12 = \frac{{(9.0\,\times \,{{{10}}^{9}})\,\,({{{10}}^{{-6}}})\,(-2\,\times \,{{{10}}^{{-6}}})}}{3}\,=\,-6\,\,\times \,\,{{10}^{{-3}}}J
Similarly, U13 = +5.4 X 10–3J and U23 = -13.5 X 10–3 J
The total potential energy is therefore U = -1.41 X 10–2 J
This negative potential energy means that external work is needed to separate the particles and place them at infinity
Illustration
Three point charges q,\,\,2q and 8q are to be placed on a 9 cm long straight line. Find the position where the charges should be placed such that the potential energy of this system is minimum. In this situation, what is the electric field at the position of the charge q due to the other two charges ?
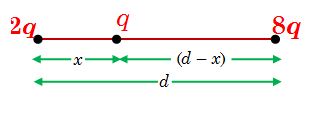
Solution
As potential energy of two point charges separated by a distance r is given by U=\left( {{{q}_{1}}{{q}_{2}}/4\pi {{\varepsilon }_{0}}r} \right) . So, to have minimum potential energy the charges of greater value should be placed farthest, i.e. q must be between 2q and 8q. Let q be at a distance x from 2q, then potential energy of the system will be
U=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left[ {\frac{{2qq}}{x}+\frac{{8qq}}{{(d-x)}}+\frac{{8q\times 2q}}{d}} \right]
For U to be minimum \left( {dU/dx} \right)=0
i.e., -\frac{{2{{q}^{2}}}}{{{{x}^{2}}}}+\frac{{8{{q}^{2}}}}{{{{{(d-x)}}^{2}}}}=0
2x = (d – x) or x = (d/3) = (9/3) = 3 cm
So to have minimum potential energy, the charge q must be placed at a distance of 3 cm from 2q between 2q and 2q, on the line joining the charges.
In this situation field at q\,\,E=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left[ {\frac{{2q}}{{{{{(3)}}^{2}}}}-\frac{{8q}}{{{{{(6)}}^{2}}}}} \right]=0 .
Illustration
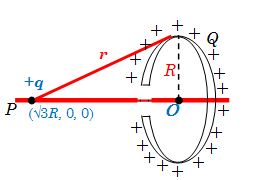
A circular ring of radius R with uniform positive charge density l per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P\,\left[ {\sqrt{3}R,\,\,0,\,\,0} \right] on the positive x- axis directly towardsO , with initial speed v. Find the smallest (non zero) value of the speed such that the particle does not return to p.
Solution
As the electric field at the centre of a ring is zero, the particle will below is not come back due to repulsion if it crosses the centre, i.e, if the in equality satisfied.
\frac{1}{2}m{{v}^{2}}+\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{qQ}}{r}>\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{qQ}}{R}
For Q=2\pi R\lambda
And r=\sqrt{{{{{(\sqrt{3}R)}}^{2}}+{{R}^{2}}}}=2R , gives
\frac{1}{2}m{{v}^{2}}>\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{2\pi R\,\lambda q}}{R}\left[ {1-\frac{1}{2}} \right]
or v>\sqrt{{\left( {\frac{{\lambda q}}{{2{{\varepsilon }_{0}}m}}} \right)}}
so {{v}_{{\min }}}=\sqrt{{\left( {\frac{{\lambda q}}{{2{{\varepsilon }_{0}}m}}} \right)}}
Practice Questions (Basic Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Main Level)
1.
A particle A has charge +q and a particle B has charge +4q with each of them having the same mass m. When allowed to fall from rest through the same electric potential difference, the ratio of their speed \frac{{{{v}_{A}}}}{{{{v}_{B}}}} will become
(a) 2 : 1
(b) 1 : 2
(c) 1 : 4
(d) 4 : 1
Ans (b)
2.
A uniform electric field E={{E}_{0}}(\hat{i}+\hat{j}) exists in the region. The potential difference \left( {{{V}_{Q}}-{{V}_{P}}} \right) between point P(0, 0) and Q (a, 0) is
(a) -{{E}_{0}}a
(b) {{E}_{0}}\sqrt{2}\,a
(c) +{{E}_{0}}a
(d) -{{E}_{0}}\sqrt{2}\,a
Ans (a)
3.
The electric potential V at any point x, y, z (all in metres) in space is given by V = 4x2 volts. The electric field (in V/m) at the point (1 m, 0, 2 m)
(a) -8\,\hat{i}
(b) 8\,\hat{i}
(c) -16\,\hat{i}
(d) 8\sqrt{5}\,\hat{i}
Ans (a)
4.
The electric potential V at any point P (x, y, z) in space is given by V = 4x2 (where V is in volt and x in meter). The electric field at the point (1m, 2m) in volt/metre is
(a) 8 along negative x-axis
(b) 8 along positive x-axis
(c) 16 along negative x-axis
(d) 16 along positive z-axis
Ans (a)
5.
Let V and E be the potential and the field respectively at a point. Which of the following assertion is correct?
(a) If V = 0, E must be zero
(b) If V¹ 0, E cannot be zero
(c) If E¹ 0, V cannot be zero
(d) none of these1
Ans (d)
6.
A charge –q is placed at the axis of a charged ring of radius r at a distance of 2\sqrt{2}\,r as shown in figure. If ring is fixed and carrying a charge Q, the kinetic energy of charge –q when it is released and reaches the centre of ring will be,
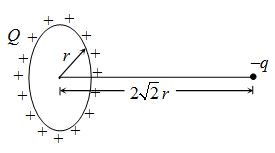
(a) \frac{{qQ}}{{4\pi {{\varepsilon }_{0}}r}}
(b) \frac{{qQ}}{{12\pi {{\varepsilon }_{0}}r}}
(c) \frac{{qQ}}{{6\pi {{\varepsilon }_{0}}r}}
(d) \frac{{qQ}}{{2\pi {{\varepsilon }_{0}}r}}
Ans (c)
7.
A conducting disc of radius R is rotating with an angular velocity Allowing the fact that electrons are the current carries in conductor, the potential difference between the centre of the disc and edge is (mass and charge of electron is m and e and neglect gravity)
(a) V=\frac{{m{{\omega }^{2}}R}}{{2e}}
(b) V=\frac{{m{{\omega }^{2}}{{R}^{2}}}}{{2e}}
(c) V=\frac{{m{{\omega }^{2}}R}}{e}
(d) V=\frac{{m{{\omega }^{2}}{{R}^{2}}}}{{4e}}
Ans (b)
Practice Questions (JEE Advance Level)
1.
The electric potential at a point (x, y) is given by: V = –Kxy. The electric field intensity at a distance r from the origin varies as
(a) r2
(b) r
(c) 2r
(d) 2r2
Ans (b)
2.
n identical charge particle are placed on the vertices of a regular polygon of n sides of side length a. One of the charge particle is released from polygon. When this particle reaches a far of distance, another particle adjacent to the first particle is released. The difference of kinetic energies of both the particles at infinity is k. Magnitude of charge is
(a) \sqrt{{4\pi {{\varepsilon }_{0}}ak}}
(b) \frac{k}{{4\pi {{\varepsilon }_{0}}a}}
(c) \frac{k}{a}
(d) \sqrt{{ka}}
Ans (a)
Q.3
An electron travelling in an electric field passes from a region of potential {{V}_{1}} to a region of potential {{V}_{2}} then
(a) no change takes place in velocity component parallel to interface of two regions
(b) direction of motion remains unchanged but speed increases
(c) direction of its motion may change but speed must decrease
(d) decrease in kinetic energy is proportional to \sqrt{{{{V}_{2}}-{{V}_{1}}}}
Ans. (a)
Q.4
Find the potential V (x, y) of an electrostatic field \vec{E}= 2axy\,\ \hat{i}\ +\ a\,({{x}^{2}}\ -\ {{y}^{2}})\ \hat{j} where a is a constant, \hat{i}\ and \ \hat{j}are the unit vectors along the x and y axes.
(a) ay\ \left( {\frac{{{{y}^{2}}}}{3}\ \,\,-\,\ {{x}^{2}}} \right)\
(b) ay\ \left( {{{y}^{2}}\ \,\,-\,\ {{x}^{2}}} \right)\
(c) ay\left( {{{y}^{2}}-{{x}^{3}}} \right)
(d) \frac{{ay}}{3}
Ans. (a)
Q.5
The electric potential decreases uniformly from V to –V along X-axis in a coordinate system as we move from a point (–x0, 0) to (x0, 0), then the electric field at the origin.
(a) must be equal to \frac{V}{{{{x}_{0}}}}
(b) may be equal to \frac{V}{{{{x}_{0}}}}
(c) must be greater than \frac{V}{{{{x}_{0}}}}
(d) must be less than \frac{V}{{{{x}_{0}}}}
Ans. (b)
Q.6
The work done by external agent in carrying a particle of a charge 2C from B(1m, 0,1m) to A(0.8m, 0.6m 1m) in a non-uniform electric field E=\left( {y\hat{i}+x\hat{j}+\hat{k}} \right)N/m along the straight line path from B to A is
(a) – 0.96 J (b) + 0.96 J (c) zero (d) – 0.48 J
Ans. (a)
Q.7
Two uniformly charged fixed identical rings are kept co-axially having charge –Q on each at a separation 2\sqrt{3}R.A Charge q is kept at the centre of one ring. The kinetic energy given to
the charge q along the axis to makes it cross the centre of the other ring is \left( {k=\frac{1}{{4\pi {{\in }_{0}}}}} \right)
(a) \frac{{kqQ}}{{\sqrt{{15}}R}}
(b) zero
(c) \frac{{kqQ}}{{\sqrt{{13}}R}}
(d) \frac{{kqQ}}{{2R}}
Ans. (c)
Q.8
Two fixed insulating rings A and B carry charges with uniform linear charge density +\lambda and -\lambda , respectively, as shown in the adjacent figure. The planes of the rings are parallel to each other and their axes are coinciding. A particle of charge “q” and mass “m” is released with zero velocity from centre P of the positively charged ring. The kinetic energy of the particle when it reaches centre Q of the negatively charged ring will be
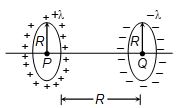
(a) \sqrt{{\frac{{2\lambda q}}{{m{{\in }_{0}}}}\left( {1-\frac{1}{{\sqrt{2}}}} \right)}}
(b) \frac{\lambda }{{{{\in }_{0}}}}\left( {1-\frac{1}{{\sqrt{2}}}} \right)q
(c) \frac{\lambda }{{2{{\in }_{0}}}}\left( {1-\frac{1}{{\sqrt{2}}}} \right)q
(d) None of these
Ans. (b)
Q.9
The grid (each square of 1m × 1m), represents a region in space containing a uniform electric field. If potentials at points O, A, B, C, D, E, F, & G, H are respectively 0, –1, –2, 1, 2, 0, –1, 1 and 0 volts, find the electric field intensity.
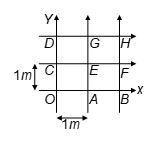
(a) (\hat{i}+\hat{j})V/m
(b) (\hat{i}-\hat{j})V/m
(c) (-\hat{i}+\hat{j})V/m
(d) (-\hat{i}-\hat{j})V/m
Ans. (b)
Q.12
Along solid non-conducting cylinder of radius R has a uniform volume charge density r. Find the potential, difference between the axis and the surface of the cylinder.
(a) \frac{{\rho {{R}^{2}}}}{{7{{\varepsilon }_{0}}}}
(b) \frac{{\rho {{R}^{2}}}}{{{{\varepsilon }_{0}}}}
(c) \frac{{\rho {{R}^{2}}}}{{6{{\varepsilon }_{0}}}}
(d) \frac{{\rho {{R}^{2}}}}{{4{{\varepsilon }_{0}}}}
Ans. (d)
Q.13
Two concentric conducting spherical shells of radii {{a}_{1}} and {{a}_{2}}\left( {{{a}_{2}}>{{a}_{1}}} \right) are charged such that their potentials are {{\varphi }_{1}} and {{\varphi }_{2}} respectively. Find the charge on the inner shell
(a) \frac{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)4\pi {{\varepsilon }_{0}}{{a}_{1}}{{a}_{2}}}}{{{{a}_{1}}-{{a}_{2}}}}
(b) \frac{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)2\pi {{\varepsilon }_{0}}.a_{1}^{2}}}{{\left( {{{a}_{1}}+{{a}_{2}}} \right)}}
(c) \frac{{\left( {{{\varphi }_{2}}+{{\varphi }_{1}}} \right){{\varepsilon }_{0}}{{a}_{1}}{{a}_{2}}}}{{4\pi \left( {{{a}_{1}}-{{a}_{2}}} \right)}}
(d) \frac{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right){{\varepsilon }_{0}}{{{\left( {{{a}_{1}}+{{a}_{2}}} \right)}}^{2}}}}{{\left( {{{a}_{1}}-{{a}_{2}}} \right)}}
Ans. (a)
Comprehension Based question ( 14 to 15)
Air breaks down (that is, the molecules rapidly become ionized and produce a spark) when the field strength is about 3 x 106 N/C. Given such a field find:
14
how long it would take an electron starting from rest to acquire a kinetic energy of 4 x 10–19 J needed to knock out an electron from a molecule
(i) 2.5 x 10–12s
(ii) 1.7 x 10–12s
(iii) 1.78 x 10–12s
(iv) 1.5 x 10–12s
Ans (iii)
15.
how far the electron would travel Neglect relativistic effects.
(i) 7.5 x 10–7m
(ii) 8.33 x 10–7m
(iii) 6.5 x 10–7m
(iv) 5.0 x 10–7m
Ans (ii)
Comprehension Based Questions ( 16 to 18)
The breakdown field strength of dry air is 3 ´ 106 N/C. At this value, what would be the potential at the surface of a charged metal sphere of radius:
16.
0.01 cm.
(i) 300 V
(ii) 200 V
(iii) 100 V
(iv) 500 V
Ans (i)
17.
1 cm.
(i) 20 kV
(ii) 10 kV
(iii) 100 kV
(iv) 30 kV
Ans (iv)
18.
1 m.
(i) 3 MV
(ii) 2 MV
(iii) 34MV
(iv) 9 MV
Ans (i)
19.
Four point charges +8 \displaystyle \mu C, -1 \displaystyle \mu C, -1 \displaystyle \mu C and +8 \displaystyle \mu C are fixed at the points -\sqrt{{27/2}} m, -\sqrt{{3/2}} m, +\sqrt{{3/2}}m and +\sqrt{{27/2}} m respectively on the y-axis. A particle of mass 6 ´ 10‑4 kg and of charge +0.1 mC moves along the –x direction. Its speed at x = +¥ is vo. Find the least value of vo for which the particle will cross the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free. Given 1/(4peo) = 9 ´ 109 Nm2/C2.
(a) 2 m/s, 0.5 mJ
(b) 8 m/s, 1.0 mJ
(c) 12 m/s, 2.0 mJ
(d) 3 m/s, 0.3 mJ
Ans(d)
Comprehension Based Question 20
A non-conducting disc of radius a and uniform positive surface charge density s is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc, from a height H with zero initial velocity. The
particle’s q/m = 4eog/s
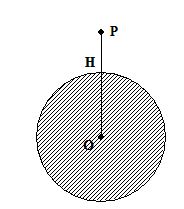
20.
Find the value of H if the particle just reaches the disc
(a) H = 5a/3
(b) H = 4a/3
(c) H = 8a/3
(d) H = 2a/3
Ans(b)
