Video Lecture
Theory For Notes Making
Physical Quantities and Units
Various laws of physics describe laws of nature. To describe the laws of physics we need some quantity, which are known as physical quantities. There are several physical quantities like mass, length, velocity, work etc. We have divided the physical quantities in two catagories
(i) Fundamental quantities
(ii) Derived Quantities
Fundamental quantities
Out of large number of physical quantities that we use in physics, there are only few quantities which are independent of all other quantities and do not require the help of any other physical quantity for their definition, therefore these are called fundamental or basic quantities. All other quantities can be expressed in terms of these quantities.
Derived quantities : All other physical quantities can be derived by suitable multiplication or division of different powers of fundamental quantities. These are therefore called derived quantities.
For example if length is defined as a fundamental quantity then area and volume are derived quantities which can be expressed in term of length.
Measurement
Physics is an experimental science and experiments involve measurement of different physical quantities in which laws of physics can be expressed. To compare the outcomes of experiments from different laboratories measurement of results of experiments is required.
Measurement can be defined as the comparision of a given physical quantity with its reference standard or its unit.
Units
The reference standard of a physical quantity that is used for the messurement of that physical quantity is called a unit.
For example for measuring length if we use a scale of 1meter, then this length 1meter will be called unit of length.
How to write the measurement
In order to express a physical quantity, the unit in which it is measured must follow its numerical value. For example, when we say that mass of a body is 50 kg, it implies that 1kg is used to measure the mass and hence the unit of mass is 1kg and the given body’s mass is 50 times that of 1kg. Hence 50 is called the numerical value and whereas kg is called the unit.
So we always write any measurement as numerical value followed by unit.
In general any Physical quantity (Q) = numerical value × Unit = n × u
Where, n represents the numerical value and u represents the unit.
As we know that some physical quantities are called fundamental quantities. The units of these quantities are called base units of the system.If the units of these quantities are defined, the units of all other quantities can be derived from them.
Points to Remember while Writing the Units of a Physical Quantity
- Even if a unit is named after a person the unit is not written with capital initial letter. Thus we write newton (not Newton) for unit of force.
- For a unit named after a person the symbol is a capital letter. Symbols of other units are not written in capital letters. For example, N for Newton (and not n) while m for metre (not M).
- The symbols or units are not expressed in plural form. Thus we write 50 m or7 erg and not 50 ms or 7 ergs.
- Not more than one solid slash is used while writting a unit. For example 1 poise should be written as
1 poise = 1g/s cm or 1 gs-1cm-1 and not 1g/s/cm.
- Full stops are not written after the abbreviations and units, e. g.,1 liter = 1000 cc (and not c. c.), emf, amu, etc.
There are different systems of units, which are used for describing measurements. They are –
(a) C G S System
(b) F P S System
(c) MKS System
(d) SI System
Almost in all the systems length,mass and time are choosen as the basic or fundamental quantities. But their units are different in different systems.
| System of units | Unit of length | Unit of mass | Unit of time |
| FPS | foot | pond | second |
| CGS | centimeter | gram | second |
| MKS | meter | kg | second |
| SI | meter | kg | second |
The system, which is widely used through out the world, is SI system, an abbreviated form of international system of units.
International System of units
In this system there are seven fundamental or base units (the unit of fundamental quantities are known as fundamental units) and two supplementary units.
Fundamental or Base Units |
| Supplementary Units | ||||
Physical Quantity | Name of The Unit | Symbol |
| Physical Quantity | Name of The Unit | Symbol |
Length | metre | m | Plane Angle | radian | rad | |
Mass | kilogram | kg | Solid Angle | steradian | sr | |
Time | second | s | ||||
Electric Current | ampere | A | ||||
Temperature | kelvin | K | ||||
Amount of substance | mole | mol | ||||
Luminous Intensity | candela | cd | ||||
Definition of base units
The metre (m): This is defined as 1650763.73 times the wavelength, in vacuum of the orange light emitted by in transition from 2p10 to 5d5.
The kilogram (kg): This is defined as the mass of a platinum-iridium cylinder kept at Sevres.
The second (s): This is the time taken by 9192631770 cycles of the radiation from the hyperfine transition in cesium – 133 when unperturbed by external fields.
The ampere (A): This is defined as the constant current which, if maintained in each of two infinitely long, straight, parallel wires of negligible cross-section placed 1 m apart, in vacuum, produces between the wires a force of 2 ´ 10-7 newton per meter length of the wires.
The Kelvin (K): In SI units, temperatures are measured on the thermodynamic scale with absolute zero as zero and the triple point of water (i.e., the temperature at which ice, water and water vapour are in equilibrium) as the upper fixed point. The interval is divided into 273.15 divisions and each division is taken as unit temperature. This unit is called the Kelvin.
The candela (cd): This is defined as the luminous intensity in the perpendicular direction of a surface of 1/600000 square metre of a full radiator at the temperature of freezing platinum under a pressure of 101325 newtons per square meter.
The mole (mol): The mole is the amount of any substance which contains as many elementary entities as there are atoms in 0.012 kg of the carbon isotope .
Measurement Of Length
There are two ways of measurement of length
(i)Direct Measurement
Where we make use of meter scale, vernier caliper or screw gauge or any other type of scale directly for the measurement of lengths of different magnitudes.
(ii) Indirect method of measurement of length
If you are asked to measure the distance of moon from the earth or the hight of a hill, it is not possible to use any scale directly to measure these lengths hence other mathematical methods have been invented to solve these problems. For example :
Reflection method:
Suppose we want to measure the distance of a multi story building from a certain point P. If a shot be fired from P, the sound of shot travels a distance x towards the building, gets reflected from the building. The reflected sound travels the distance x to the point P again, when an echo of the shot is heard.
Let t = time interval between the firing of the shot and echo sound.
v = velocity of sound in air.
Distance = velocity x time
x + x = (v) . (t)
hence \displaystyle \text{x = }\frac{{\text{v}.t}}{2}
As v is known, x can be calculated by measuring the time t.
Parallex method:
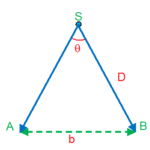
This method is used for measuring distance of nearby stars.If we have to measure the distance D of a far away star S by this method. We observe this star from two different position A and B on the earth, separated by a distance AB = b at the same time as shown in figure. Let ASB =, the angle is called parallatic angle. As the star is very far away, b/D << 1 and is very small.
Here we can take AB as an arc of length b of a circle with centre at S and the distance D as the radius AS=BS so that AB = b = D.q , where q is in radians.
therefore D = b/q
Knowing b and measuring q, we can calculate D.
MEASUREMENT OF MASS
Measurement of Inertial Mass
Inertial mass of a body is measured using a device which is known as inertial balance. It consists of a long metal strip. One end of the strip is clamped to a table such that its flat face is vertical, and it can easily vibrate horizontally as you can see below. The other end of strip supports a pan in which the object whose inertial mass is to be found can be kept.
It is found that the square of time period of vibration is directly proportional to total mass of the pan and the body placed in it.
\displaystyle {{t}^{2}}\propto m\,
therefore \displaystyle \frac{{t_{2}^{2}}}{{t_{1}^{2}}}=\frac{{{{m}_{2}}}}{{{{m}_{1}}}}
hence \displaystyle {{m}_{2}}={{m}_{1}}\frac{{t_{2}^{2}}}{{t_{1}^{2}}}
Measurement of Time: The following methods are used
- Quartz Crystal Clock
- Atomic Clock
- Radioactive dating
Dimensions
All the physical quantities of interest can be derived from the fundamental quantities. When a quantity is expressed in terms of the fundamental quantities, it is written as a product of different power of the fundamental quantities. The exponent of a fundamental quantity that enters into the expression is called the dimension of the quantity. Take an example to understand the concept of dimension. All of us know about velocity, which is roughly defined as length divided by time interval. Thus the velocity is expressed in terms of fundamental quantities length and time as
Velocity = \displaystyle \frac{{length}}{{time}} = length(time)-1
Here some exponent of fundamental quantities enter into the expression, are called the dimensions of the physical quantity velocity. Thus the dimension of velocity is 1 in length and -1 in time. For our convenience the fundamental quantities are represented by one-letter symbols. Generally mass is denoted by M, length by L, time by T, electric current by I, temperature by K, amount of substance by mol and luminous intensity by cd. Using this the dimension of velocity is written as velocity=[LT-1] or [M0L1T-1] which is called in another way dimensional formula of velocity.
Dimensions of few quantities
Area | Length x breadth | L x L = [L2] |
Density | Mass/volume | [ML-3] |
Acceleration | change in velocity/time interval | [M0LT-2] |
Force | F = ma | [MLT–2] |
Linear momentum | P = mv | [MLT–1] |
Pressure | P = F/A | [ML–1T–2] |
Universal gravitational constant | \displaystyle G=\frac{{F\times {{r}^{2}}}}{{{{m}_{1}}\times {{m}_{2}}}} | [M–1L3T–2] |
Work | W = F x d | [ML2T–2] |
Kinetic Energy or Any type of energy | \displaystyle KE=\frac{1}{2}m{{v}^{2}} | [ML2T–2] |
Surface tension | T= F/ l | [ML°T–2] |
Strain | \displaystyle \frac{{\text{change in dimension}}}{{\text{actual dimension}}} | [M°L°T°] |
Modulus of elasticity | \displaystyle \frac{{stress}}{{strain}} | [ML–1T–2] |
Angle | \displaystyle \frac{{arc}}{{radius}} | [M°L°T°] |
Coefficient of viscosity | \displaystyle \eta =\frac{F}{{6\pi rv}} | [M1L–1T–1] |
Planck’s constant | \displaystyle \text{h = }\frac{E}{\nu } | [ML2T–1] |
Some Quantities from Heat with their units
Quantity | Unit | Dimension |
Temperature (T) | Kelvin | [M0L0T0 K1] |
Heat (Q) | Joule | [ML2T– 2] |
Specific Heat (c) | Joule/kg-K | [M0L2T– 2 K–1] |
Thermal capacity | Joule/K | [M1L2T – 2 K–1] |
Latent heat (L) | Joule/kg | [M0L2T – 2] |
Gas constant (R) | Joule/mol–K | [M1L2T– 2 K– 1] |
Boltzmann constant (k) | Joule/K | [M1L2T– 2 K– 1] |
Coefficient of thermal conductivity (K) | Joule/m-s-K | [M1L1T– 3 K– 1] |
Stefan’s constant (s) | Watt/m2–K4 | [M1L0T– 3 K– 4] |
Wien’s constant (b) | Metre-K | [M0L1T 0K 1] |
Planck’s constant (h) | Joule-s | [M1L2T–1] |
Coefficient of Linear Expansion (a) | Kelvin–1 | [M0L0T0 K–1] |
Mechanical equivalent of Heat (J) | Joule/Calorie | [M0L0T0] |
Vander wall’s constant (a) | Newton-m4 | [ML5T– 2] |
Vander wall’s constant (b) | m3 | [M0L3T0] |
Some Quantities from Electricity and Magnetism
Quantity | Unit | Dimension |
Electric charge (q) | Coulomb | [M0L0T1A1] |
Electric current (I) | Ampere | [M0L0T0A1] |
Capacitance (C) | Coulomb/volt or Farad | [M–1L– 2T 4A2] |
Electric potential (V) | Joule/coulomb | [M1L2T–3A–1] |
Permittivity of free space (e0) | \displaystyle \frac{{coulom{{b}^{2}}}}{{newton-mete{{r}^{2}}}} | [M–1L–3T 4A2] |
Dielectric constant (K) | Unitless | [M0L0T0] |
Resistance (R) | Volt/Ampere or ohm | [M1L2T– 3A– 2] |
Resistivity or Specific resistance (r) | Ohm-metre | [M1L3T– 3A– 2] |
Coefficient of Self-induction (L) | \frac{{volt-second}}{{ampere}} or henry or ohm-second | [M1L2T– 2A– 2] |
Magnetic flux (f) | Volt-second or weber | [M1L2T–2A–1] |
Magnetic induction (B) | \frac{{newton}}{{ampere-metre}} or \frac{{Joule}}{{ampere-metr{{e}^{2}}}} or \frac{{volt-\text{second}}}{{metr{{e}^{2}}}} or Tesla | [M1L0T– 2A– 1] |
Magnetic Intensity (H) | Ampere/metre | [M0L– 1T0A1] |
Magnetic Dipole Moment (M) | Ampere-metre2 | [M0L2T0A1] |
Permeability of Free Space (m0) | \frac{{Newton}}{{amper{{e}^{2}}}} or \frac{{Joule}}{{amper{{e}^{2}}-metre}} or \frac{{Volt\sec }}{{Am}} or \frac{{Ohm-\sec ond}}{{metre}} or \frac{{henry}}{{metre}} | [M1L1T–2A–2] |
Surface charge density (s) | Coulomb\,metr{{e}^{{-2}}} | [M0L–2T1A1] |
Electric dipole moment (p) | Coulomb-metre | [M0L1T1A1] |
Conductance (G) (1/R) | oh{{m}^{{-1}}} | [M–1L–2T3A2] |
Conductivity (s) or (1/r) | oh{{m}^{{-1}}}metr{{e}^{{-1}}} | [M–1L–3T3A2] |
Current density (J) | Ampere/m2 | M0L–2T0A1 |
Intensity of electric field (E) | Volt/metre, Newton/coulomb | M1L1T –3A–1 |
Rydberg constant (R) | m–1 | M0L–1T0 |
Few Important Points
(i) The dimensions of a physical quantity do not depend on the system of units.Hence all unitless quantities are dimensionless but all dimensionless quantities are not unitless like angle is dimensionless but its SI unit is radian.
(ii) A physical quantity that does not have any unit must be dimensionless.
(iii) All constants are not dimensionless like acceleration due to gravity g' , Universal gravitational constant `G’. But the mathematical costants which are pure numbers are dimensionless like 1,2,3,… or p.
(iv) It is wrong to say that the dimensions of force are MLT–2. Actually we should say that the dimensional formula for force is MLT–2 and that the dimensions of force are 1 in mass, 1 in length and –2 in time.
(v) Physical quantities defined as the ratio of two similar quantities are dimensionless.
(vi) In any physical relation the terms having logarithmic, exponential or trigonometric functions are always dimensionless.
Illustration
We know that force is defined as product of mass and acceleration. Find the unit of force?
Solution
Here, Force = mass x acceleration
but \displaystyle acceleration=\frac{{change\text{ }in\text{ }velocity}}{{time\text{ interval}}}
therefore Force = mass velocity (time)-1
= mass length (time)-2
As the unit of mass, length and time is kg, m and s respectively, hence the unit of force is kg ms-2, which is called newton and 1 newton=1kg ms-2 .
Illustration
A physical quantity called energy (E), is defined as E = mv2 where m is the mass and v is the speed. Find the unit of energy?
Solution
Here, E = mass (speed)2
=(mass) (length)2 (time)-2
Hence the unit of energy is kg m2s-2 which is called joule(J) and1J=1kg m2s-2.
Illustration
Find the dimensional formula of Force?
Solution
Force is defined as
Force = mass acceleration
= mass length (time)-2
So the dimensional formula of force is given by
[Force]=[MLT-2].
Illustration
Find the dimensional formula of energy?
Solution
Since energy is defined as
Energy =(mass) (speed)2
= (mass) (length)2 (time)-2
Here is a number and has no dimension, hence the dimensional formula of energy is given by
[Energy] = [ML2T-2].
Illustration
Find the dimensions of resistivity, thermal conductivity and coefficient of viscosity.from the relations \displaystyle R=\rho \frac{L}{A}, \displaystyle \frac{{dQ}}{{dt}}=\frac{{\Delta \theta kA}}{L}and \displaystyle F=\eta A\frac{{dv}}{{dx}}
where R = electrical resistance , r = resitivity , A = area , l = length, dQ = heat , dt = time, Dq = change in temperature, F = Force, dv = change in velocity, dx = small distance, k = Thermal conductivity, h = Coefficient of viscosity
Solution
(i) \displaystyle R=\rho \frac{\ell }{A} hence \displaystyle \rho =R\frac{A}{L}
but \displaystyle R=\frac{V}{I}\text{ and potential difference V=}\frac{{Work}}{{ch\arg e}}=\frac{{\left[ {M{{L}^{2}}{{T}^{{-2}}}} \right]}}{{\left[ {AT} \right]}}=\left[ {M{{L}^{2}}{{T}^{{-3}}}{{A}^{{-1}}}} \right]
therefore \displaystyle R=\frac{{\left[ {M{{L}^{2}}{{T}^{{-3}}}{{A}^{{-1}}}} \right]}}{A}=\left[ {M{{L}^{2}}{{T}^{{-3}}}{{A}^{{-2}}}} \right]
Now \displaystyle \rho =R\frac{A}{L}
So \displaystyle \rho =R\frac{A}{L}=[M{{L}^{2}}{{T}^{{-3}}}{{A}^{{-2}}}]\frac{{{{L}^{2}}}}{L}
finally we get \displaystyle \rho =[M{{L}^{3}}{{T}^{{-3}}}{{A}^{{-2}}}]
(ii) Thermal conductivity, k
\displaystyle \frac{{dQ}}{{dt}}=\frac{{\Delta \theta kA}}{L}
therefore \displaystyle k=\frac{{dQ\times L}}{{dt\times \Delta \theta \times A}}
hence \displaystyle k=\frac{{\left[ {M{{L}^{2}}{{T}^{{-2}}}} \right]\times \left[ L \right]}}{{\left[ T \right]\times \left[ K \right]\times \left[ {{{L}^{2}}} \right]}}
k = \displaystyle =[ML{{T}^{{-3}}}{{K}^{{-1}}}]
(iii) Coefficient of viscosity,
\displaystyle F=\eta A\frac{{dv}}{{dx}}
\displaystyle \eta =\frac{{Fdx}}{{Adv}}=\frac{{[ML{{T}^{{-2}}}]\times [L]}}{{[{{L}^{2}}]\times [L{{T}^{{-1}}}]}}=[M{{L}^{{-1}}}{{T}^{{-1}}}].
Illustration
The dimensional representation of Planck’s constant is identical to that of
(A) Torque
(B) Power
(C) Linear momentum
(D) angular momentum
Solution
As Planck’s constant has dimensions of \displaystyle \frac{E}{\nu }
\displaystyle =\frac{{[M{{L}^{2}}{{T}^{{-2}}}]}}{{[{{T}^{{-1}}}]}}
= [ML2T-1]
and Dimensions of angular momentum = r x p
= [L ]x [MLT–1]
= [ML2T-1]
Hence answer is (D)
Illustration
Choose the wrong statement(s)
(a) A quantity which has dimensions must also have unit
(b)A quantity which has unit must also have dimension
(c)A dimensionless quantity cannot have units
(d)A unitless quantity may have dimensions
Solution
Statement (a) is correct
Statement (b) is wrong. Example is angle which has unit radian but has no dimensions
Statement (c) is wrong. Example is again angle
Statement (d) is wrong. Because no units means no dimensions
Hence (b),(c),(d) is the answer
Objective Assignment
- Candela is the unit of
(a) Electric intensity
(b) Luminous intensity
(c) Sound intensity
(d) None of these
Ans :(b)
- The unit of Planck’s constant is
(a) Joule
(b) Joule/s
(c) Joule/m
(d) Joule-s
Ans :(d)
- The S.I. unit of gravitational potential is
(a) J
(b) J-kg-1
(c) J-kg
(d) J-kg-2
Ans :(b)
4. The unit of L / R is (where L = inductance and R = resistance)
(a) sec
(b) sec-1
(c) Volt
(d) Ampere
Ans :(a)
5. Which is different from others by units
(a) Phase difference
(b) Mechanical equivalent
(c) Loudness of sound
(d) Poisson’s ratio
Ans :(d)
6. One Mach number is equal to
(a) Velocity of light
(b) Velocity of sound 332m/sec
(c) 1km/sec
(d) 1m/sec
Ans :(b)
7. The unit of surface tension in SI system is
(a) dyne/cm2
(b) newton/m
(c) dyne/cm
(d) newton/m2
Ans :(b)
8. The SI unit of momentum is
(a) kg/m
(b) kg-m/sec
(c) kg-m2/sec
(d) kg-newton
Ans :(b)
9. erg-m-1 can be the unit of measure for
(a) Force
(b) Momentum
(c) Power
(d) Acceleration
Ans :(a)
10. Light year is a unit of
(a) Time
(b) Mass
(c) Distance
(d) Energy
Ans :(c)
11. Which of the following is not represented in correct unit
(a) \frac{{\text{Stress}}}{{\text{Strain}}}=N/{{m}^{2}}
(b) Surface tension =N/m
(c) Energy = kg-m/sec
(d) Pressure = N/m2
Ans :(c)
12. Wavelength of ray of light is 0.00006m . It is equal to
(a) 6micron
(b) 60micron
(c) 600micron
(d) 0.6micron
Ans :(b)
13. Which pair has the same dimensions
(a) Work and power
(b) Density and relative density
(c) Momentum and impulse
(d) Stress and strain
Ans :(c)
14. The dimensions of universal gravitational constant are
(a) {{M}^{{-2}}}{{L}^{2}}{{T}^{{-2}}}
(b) {{M}^{{-1}}}{{L}^{3}}{{T}^{{-2}}}
(c) M{{L}^{{-1}}}{{T}^{{-2}}}
(d) M{{L}^{2}}{{T}^{{-2}}}
Ans :(b)
15. The dimensional formula of angular velocity is
(a) {{M}^{0}}{{L}^{0}}{{T}^{{-1}}}
(b) ML{{T}^{{-1}}}
(c) {{M}^{0}}{{L}^{0}}{{T}^{1}}
(d) M{{L}^{0}}{{T}^{{-2}}}
Ans :(a)
16. Dimensional formula for angular momentum is
(a) M{{L}^{2}}{{T}^{{-2}}}
(b) M{{L}^{2}}{{T}^{{-1}}}
(c) ML{{T}^{{-1}}}
(d) {{M}^{0}}{{L}^{2}}{{T}^{{-2}}}
Ans :(b)
17. Dimensional formula M{{L}^{{-1}}}{{T}^{{-2}}} does not represent the physical quantity
(a) Young’s modulus of elasticity
(b) Stress
(c) Strain
(d) Pressure
Ans :(c)
18. The dimensions of calorie are
(a) M{{L}^{2}}{{T}^{{-2}}}
(b) ML{{T}^{{-2}}}
(c) M{{L}^{2}}{{T}^{{-1}}}
(d) M{{L}^{2}}{{T}^{{-3}}}
Ans :(a)
19. The dimensional formula for impulse is
(a) ML{{T}^{{-2}}}
(b) ML{{T}^{{-1}}}
(c) M{{L}^{2}}{{T}^{{-1}}}
(d) {{M}^{2}}L{{T}^{{-1}}}
Ans :(b)
20. The dimensional formula for Planck’s constant `h’ is
(a) M{{L}^{{-2}}}{{T}^{{-3}}}
(b) M{{L}^{2}}{{T}^{{-2}}}
(c) M{{L}^{2}}{{T}^{{-1}}}
(d) M{{L}^{{-2}}}{{T}^{{-2}}}
Ans :(c)
21. Out of the following, the only pair that does not have identical dimensions is
(a) Angular momentum and Planck’s constant
(b) Moment of inertia and moment of a force
(c) Work and torque
(d) Impulse and momentum
Ans :(b)
22. Planck’s constant has the dimensions (unit) of
(a) Energy
(b) Linear momentum
(c) Work
(d) Angular momentum
Ans :(d)
23. If V denotes the potential difference across the plates of a capacitor of capacitance C, the dimensions of CV2 are
(a) Not expressible in MLT
(b) ML{{T}^{{-2}}}
(c) {{M}^{2}}L{{T}^{{-1}}}
(d) M{{L}^{2}}{{T}^{{-2}}}
Ans :(d)
24. The dimensions of resistivity in terms of M,L,T and Q where Q stands for the dimensions of charge, is
(a) M{{L}^{3}}{{T}^{{-1}}}{{Q}^{{-2}}}
(b) M{{L}^{3}}{{T}^{{-2}}}{{Q}^{{-1}}}
(c) M{{L}^{2}}{{T}^{{-1}}}{{Q}^{{-1}}}
(d) ML{{T}^{{-1}}}{{Q}^{{-1}}}
Ans :(a)
25. Dimensional formula of velocity of sound is
(a) {{M}^{0}}L{{T}^{{-2}}}
(b) L{{T}^{0}}
(c) {{M}^{0}}L{{T}^{{-1}}}
(d) {{M}^{0}}{{L}^{{-1}}}{{T}^{{-1}}}
Ans :(c)
26. The dimensions of “time constant” \frac{L}{R} during growth and decay of current in all inductive circuit is same as that of
(a) Constant
(b) Resistance
(c) Current
(d) Time
Ans :(d)
27. Which one has the dimensions different from the remaining three
(a) Power
(b) Work
(c) Torque
(d) Energy
Ans :(a)
28. The dimension of \frac{1}{{\sqrt{{{{\varepsilon }_{0}}{{\mu }_{0}}}}}} is that of
(a) Velocity
(b) Time
(c) Capacitance
(d) Distance
Ans :(a)
Subjective Assignment
1.
Name the SI unit of (i) temperature and (ii) electric current.
2.
Name and define the SI unit of luminous intensity.
3.
Define international standard of mass.
4.
Name the system of units that is not based on units of mass, length and time alone.
5.
What is the SI unit and dimensional formula of thermal conductivity and electron mobility?
6.
Write three dimensionless quantities with their units.
7.
List the SI based fundamental quantities and write their units with symbols.
8.
What are different systems of units? What is the unit of energy in CGS system?
9.
What is system of units? Mention some of them.
10.
What is the necessity of selecting some units as fundamental units?
11.
A star is located 9 light years from us. What is the distance in parsec?
Ans : 3.26 ly = 1 parsec , so 1 ly = 1/3.26 parsec, Hence 9 ly = 9 x (1/3.26) = 2.76 parsec
12.
Define 1 light year and write its value.
13.
Define astronomical units and write its value.
14.
What is meant by RADAR and SONAR? How are long distances measured using these techniques?
15.
Write two constants which has both units and dimensions.
16.
Express parsec in light years.
Ans : 1 parsec = 3.26 ly
17.
Why a number of units are made for a single quantity like length or mass.
18.
Astronomical unit (AU) is the average distance between the earth and the sun, approximately 1.5 x 1011 m. The speed of light is about 3×108 m/s. What is the speed of light in astronomical unit per minute?
Ans : 0.12 AU/min
19.
Define astronomical unit and parsec.
20.
The shadow of a tower standing on a level plane is found to be 50 m longer when suits altitude is 30º than when it is 60º. Find the height of the tower.
Ans : h = 25√3 m
21.
Calculate the parallax of a star at the distance of 2 ly when viewed from two locations of earth six months apart in its orbit around sun.
Ans : 0.16×10-4 rad
22.
Explain parallax method of measuring distance of a nearest star from the surface of earth.
23.
Suggest an indirect method for measuring the height of a tree on a sunny day.
24.
A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1” (second) of arc from opposite ends of a baseline equal to the distance from the earth to the sun. How much is parsec in terms of metres? What is the order of parsec?
25.
The unit of length convenient on the atomic scale is known as an angstrom and is denoted by
Å (1Å = 10-10m). The size of a hydrogen atom is about 0.5 Å. What is the total atomic volume in of one mole hydrogen atoms?
Ans : Hint : Avogadro number x volume of one atom = Approx 3.15×10-7 m3
26.
The moon subtends an angle of 57 minutes at the base-line equal to the radius of the earth. What is the distance of the moon from the earth ? Radius of the earth = 6400km.
Ans : 386188.4 km ;
Hint: angle in radians = arc / radius
27.
The parallax of a heavenly body measured from two points diametrically opposite on equator of earth is 1.0 minute. If the radius of the earth is 6400 km, find the distance of the heavenly body from the centre of the earth in AU.
Ans : 0.293 AU , Hint: angle in radians = arc / radius
28.
A satellite is observed from two points A and B at a distance 1.3xl07 m apart on earth. If angle subtended at the satellite is 1°30′, find distance of the satellite from earth.
Ans : 4.96 x 105 km
29.
Explain the method of measuring the size of oleic acid molecule.
30.
What are the dimensions of work in S.I. system and C.G.S. system of units
Ans : Dimensions of a quantity remains same in all systems hencs the dimensions of work is [ML2T-2].
