Video Lecture
Theory For Notes Making
Collision
Collision may be considered as a phenomenon of observation of mutual action and reaction force of great magnitude between particles for a very short interval of time. Collision is a brief event between objects that interact each other through a force which may be a contact force or field force. The interaction between two or more objects is called a collision if there exists three identifiable stages to this interaction: before, during and after. In the before and after stage the interaction forces are zero or approaches zero asymptotically. Between these two states the interaction forces are large and often the dominating forces governing the object’s motion. The magnitude of the interacting force is often unknown. Therefore, the conservation of momentum statement is useful for relating the initial velocities before the interaction to the final velocities after the interaction without requiring a detailed knowledge of the interaction forces.
Types of Collision
(i)
Elastic collision
( Linear Momentum and kinetic energy both are conserved)
(ii)
Inelastic collision
(Linear Momentum is conserved but kinetic energy is not conserved)
(iii)
Perfectly Inelastic collision
( Linear Momentum is conserved and there is a maximum loss of kinetic energy)
So collisions may be either elastic or inelastic. Linear momentum is conserved in both cases. A perfectly elastic collision is defined as one in which the total kinetic energy of the particles is also conserved hence the equation of kinetic energy conservation may be written as follows
\frac{1}{2}{{m}_{1}}u_{1}^{2}+\frac{1}{2}{{m}_{2}}u_{2}^{2}=\frac{1}{2}{{m}_{1}}v_{1}^{2}+\frac{1}{2}{{m}_{2}}v_{2}^{2}
In an inelastic collision, the total kinetic energy of the particle changes. Some of the kinetic energy is stored as potential energy associated with a change in internal structure or state, and is not immediately recovered. Some of the energy may be used to raise the system (e.g. an atom) to a state with higher energy. Or, it may be converted into thermal energy of vibrating atoms and molecules or into light, sound or some other from of energy.In a completely inelastic collision, the two bodies couple or stick together.
Coefficient of Restitution
It is defined as the ratio of velocity of separation to the velocity of approach of the two colliding bodies
According to Newton’s experimental law on collisions of two bodies the relative velocity of any one of the colliding bodies relative to the other body after impact is proportional to the relative velocity of the same body before impact but opposite in direction. The constant of proportionality is called the ‘coefficient of restitution’ and it is generally denoted by ‘e’. Thus
v12(after impact) = –e × u12 (before impact) where v12 and u12 stands for the final and initial relative velocity of 1 with respect to 2.
So Coefficient of Restitutione = \frac{{\text{velocity}\,\,\text{of}\,\text{separation}}}{{velocity\,of\,appraoch}}=\left| {\frac{{{{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}}}}{{{{{\vec{u}}}_{1}}-{{{\vec{u}}}_{2}}}}} \right|
Generally e is less than 1. When e = 1, collision is said to be ‘perfectly elastic’. It is to be remembered that when collision takes place between a particle and a smooth heavy wall, only the perpendicular components of velocities before and after impact are subject to Newton’s law and not the ones parallel to the wall. The components of velocities before and after impact parallel to the wall remain unaltered.
Head-on elastic collision [one dimensional elastic collision]
Consider two bodies A and B of masses m1 and m2 respectively moving along the same straight line in the same direction. Let u1 and u2 be their respective magnitudes of velocities such that u1> u2
The two bodies will collide after some time.
Let v1 and v2 be the magnitude of velocities of A and B respectively after the collision.

Applying the law of conservation of momentum,
total momentum before collision = total momentum after collision
{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} (in magnitude)
or {{m}_{1}}({{u}_{1}}-{{v}_{1}})={{m}_{2}}({{v}_{2}}-{{u}_{2}}) …(i)
Since the collision is elastic therefore kinetic energy will be conserved.
Kinetic energy before collision = Kinetic energy after collision
\frac{1}{2}{{m}_{1}}{{u}_{1}}_{{}}^{2}+\frac{1}{2}{{m}_{2}}{{u}_{2}}_{{}}^{2}=\frac{1}{2}{{m}_{1}}{{v}_{1}}_{{}}^{2}+\frac{1}{2}{{m}_{2}}{{v}_{2}}_{{}}^{2}
or {{m}_{1}}({{u}_{1}}+{{v}_{1}})\,({{u}_{1}}-{{v}_{1}})\,={{m}_{2}}({{v}_{2}}+{{u}_{2}})\,({{v}_{2}}-{{u}_{2}}) …(ii)
Dividing (ii) by (i), we get
{{u}_{1}}+{{v}_{1}}={{v}_{2}}+{{u}_{2}}
or {{u}_{1}}-{{u}_{2}}={{v}_{2}}-{{v}_{1}} …(iii)
\displaystyle ({{u}_{1}}-{{u}_{2}}) is the magnitude of the relative velocity of A with respect to B i.e. relative velocity before the collision. Whereas ({{v}_{2}}-{{v}_{1}}) is the magnitude of relative velocity of B with respect to A after the collision. It may be noted that the direction of relative velocity is reversed after the collision.
From equation (iii), {{v}_{2}}={{u}_{1}}-{{u}_{2}}+{{v}_{1}} , let’s put it in equation (i)
From equation (i),
{{m}_{1}}({{u}_{1}}-{{v}_{1}})={{m}_{2}}({{u}_{1}}-{{u}_{2}}+{{v}_{1}}-{{u}_{2}})
on solving for v1 we get \displaystyle {{v}_{1}}=\frac{{{{m}_{1}}-{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{1}}+\frac{{2{{m}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{2}} …(iv)
Again, from equation (iii),
{{v}_{1}}={{v}_{2}}-{{u}_{1}}+{{u}_{2}}
Substituting this value in equation (i) and simplifying, we get
{{v}_{2}}=\frac{{{{m}_{2}}-{{m}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{2}}+\frac{{2{{m}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}{{u}_{1}} …(v)
Special Cases Of Elastic One Dimensional Collision
(i)
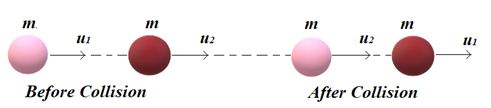
When two bodies of equal masses collide elastically head-on, their velocity will interchange as shown in the figure given below
(ii)
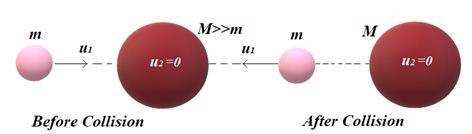
When a very light body of very small mass collide elastically head-on with a stationary heavy body of very large mass then the lighter body rebound with the same speed whereas the heavy body remains stationary.
(iii)
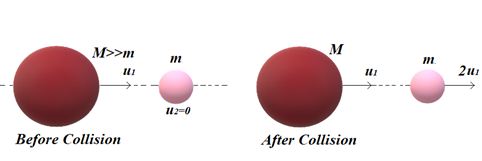
When a very heavy body of very large mass collide elastically head-on with a stationary light body of very small mass then the heavy body continues to move with the same initial speed the lighter body moves with a speed double that of the initial velocity of the heavier body.
Perfectly Inelastic Collision
In this type of collision the two bodies acquire equal velocity along the line of impact after the collision . One of the example of this type of collision is when the two bodies stick together after the collision. Consider two masses m1 and m2 moving along the same line with speed u1 and u2 in the same direction as shown in the figure.
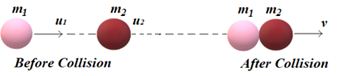
Elastic collision in two dimensions (Oblique collision)
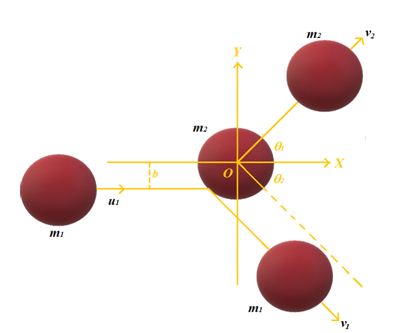
Consider two masses m1 and m2 collide with a impact parameter b. Initially m1 is moving with speed u1 whereas the mass m2 is at rest .
Applying the law of conservation of momentum to the x-component of motion, we get
{{m}_{1}}{{u}_{1}}={{m}_{1}}{{v}_{1}}\cos {{\theta }_{1}}+{{m}_{2}}{{v}_{2}}\cos {{\theta }_{2}} …(i)
For y-component of motion,
{{m}_{1}}{{v}_{1}}\sin {{\theta }_{1}}-{{m}_{2}}{{v}_{2}}\sin {{\theta }_{2}}=0 …(ii)
The collision is elastic. So kinetic energy will be conserved.
\frac{1}{2}{{m}_{1}}{{u}_{1}}_{{}}^{2}=\frac{1}{2}{{m}_{1}}{{v}_{1}}_{{}}^{2}+\frac{1}{2}{{m}_{2}}{{v}_{2}}_{{}}^{2}
or {{m}_{1}}{{u}_{1}}_{{}}^{2}={{m}_{1}}{{v}_{1}}_{{}}^{2}+{{m}_{2}}{{v}_{2}}_{{}}^{2} …(iii)
The equations (i), (ii) and (iii) can be used to solve this problem.
Special case : If {{m}_{1}}={{m}_{2}} and {{u}_{2}}=0 substituting these values in equation (i), (ii) and (iii) we get
{{u}_{1}}={{v}_{1}}\cos {{\theta }_{1}}+{{v}_{2}}\cos {{\theta }_{2}} …(iv)
0={{v}_{1}}\sin {{\theta }_{1}}-{{v}_{2}}\sin {{\theta }_{2}} …(v)
And u_{1}^{2}=v_{1}^{2}+v_{2}^{2} …(vi)
Squaring (iv) and (v) and adding we get
u_{1}^{2}=v_{1}^{2}+v_{2}^{2}+2{{v}_{1}}{{v}_{2}}\cos ({{\theta }_{1}}+{{\theta }_{2}}) …(vii)
Using (vi) and (vii) we get \displaystyle \cos ({{\theta }_{1}}+{{\theta }_{2}})=0
{{\theta }_{1}}+{{\theta }_{2}}=\pi /2
i.e. after perfectly elastic oblique collision of two bodies of equal masses (if the second body is at rest), the scattering angle {{\theta }_{1}}+{{\theta }_{2}} would be {{90}^{o}}.
Illustration
A ball moving with a speed of 9m/s strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of 30° with the original line of motion. Find the speeds of the two balls after collisions.
Solution:
Here, {{m}_{1}}={{m}_{2}}=m, {{u}_{1}}=9\,\text{m/s},{{u}_{2}}=0
{{\theta }_{1}}={{\theta }_{2}}=30{}^\circ ,{{v}_{1}}=?{{v}_{2}}=?
Applying principle of conservation of linear momentum
(i)
along the direction of motion (X-axis) {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}\cos {{\theta }_{1}}+{{m}_{2}}{{v}_{2}}\cos {{\theta }_{2}}
m\times 9+0=m{{v}_{1}}\cos 30{}^\circ +m{{v}_{2}}\cos 30{}^\circ
or, 9={{v}_{1}}\sqrt{3}/2+{{v}_{2}}\sqrt{3}/2=\frac{{({{v}_{1}}+{{v}_{2}})\sqrt{3}}}{2}
{{v}_{1}}+{{v}_{2}}=\frac{{18}}{{\sqrt{3}}} …(i)
(ii)
along a direction perpendicular to the direction of motion (Y-axis)
0+0={{m}_{1}}{{v}_{1}}\sin {{\theta }_{1}}-{{m}_{2}}{{v}_{2}}\sin {{\theta }_{2}}
{{m}_{1}}{{v}_{1}}\sin {{\theta }_{1}}={{m}_{2}}{{v}_{2}}\sin {{\theta }_{2}}
m{{v}_{1}}\sin 30{}^\circ =m{{v}_{2}}\sin 30{}^\circ
{{v}_{1}}={{v}_{2}}
Put in (i) 2{{v}_{1}}=\frac{{18}}{{\sqrt{3}}}
{{v}_{1}}=\frac{9}{{\sqrt{3}}}=\frac{{9\sqrt{3}}}{{\sqrt{3}\sqrt{3}}}=3\sqrt{3}\ \text{m/s}
Hence the two balls move with the same velocity \displaystyle =3\sqrt{3}\ \text{m/s} after collision. Ans.
Illustration
A railway carriage of mass 10000 kg moving with a speed of 15ms–1 strikes a stationary carriage of the same mass. After the collision, the carriages get coupled and move together. What is their common speed after collision?
Solution:
Here, {{m}_{1}}=10000kg, {{v}_{1}}=15\text{m}{{\text{s}}^{{-1}}} , {{m}_{2}}=10000kg,\ {{v}_{2}}=0,\ v=?
As the collision is perfectly inelastic, therefore,
({{m}_{1}}+{{m}_{2}})v={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}
(10000+10000)v=10000\times 15+0
v=\frac{{10000\times 15}}{{20000}}=7.5\text{m}{{\text{s}}^{{-1}}}.
Illustration
A ball of 0.1 kg makes an elastic head on collision with a ball of unknown mass initially at rest. If the 0.1 kg ball rebounds at one third of its original speed, what is the mass of the other ball?
Solution:
Here, {{m}_{1}}=0.1\text{kg}\ {{m}_{2}}=?
{{u}_{2}}=0 Let {{u}_{1}}=u;
As {{v}_{1}}=\frac{{({{m}_{1}}-{{m}_{2}}){{u}_{1}}}}{{{{m}_{1}}+{{m}_{2}}}}+\frac{{2{{m}_{2}}{{u}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}
{{v}_{1}}=-\frac{u}{3}
-\frac{u}{3}=\frac{{(0.1-{{m}_{2}})u}}{{0.1+{{m}_{2}}}}
or -\frac{1}{3}=\frac{{0.1-{{m}_{2}}}}{{0.1+{{m}_{2}}}}
or -0.3+3{{m}_{2}}=0.1+{{m}_{2}}
2{{m}_{2}}=0.1+0.3=0.4
{{m}_{2}}=\frac{{0.4}}{2}\text{kg}.=0.2\text{kg}\text{.}
Objective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
