Video Lecture
Theory For Notes Making
Centre of mass
It is a point inside or outside of a body where the whole mass of the body is suppose to be concentrated. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion.The centre of mass of a body or a system of bodies is the point that moves as through all of the mass were concentrated there.This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. This may also be defined as a point where the body can be balanced by simply giving a support at this point.
The centre of mass of a bat lies along the bat’s central axis. One can locate it by balancing the bat horizontally on an outstretched finger or any small support as shown in the figure. The centre of mass is on the bat’s axis just above the finger or support.

Location Of Centre of mass
For a system of n particles whose position vectors are \displaystyle {{\vec{r}}_{1}},{{\vec{r}}_{2}},………{{\vec{r}}_{n}} as shown in the figure,
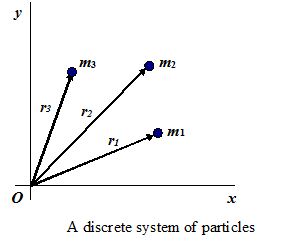
the position vector for the center of mass {{\text{vec{ r}}}_{{\text{cm}}}} is defined as
\displaystyle {{\vec{r}}_{{cm}}}=\frac{{{{m}_{1}}{{{\vec{r}}}_{1}}+{{m}_{2}}{{{\vec{r}}}_{2}}+……+{{m}_{n}}{{{\vec{r}}}_{n}}}}{{{{m}_{1}}+{{m}_{2}}+……+{{m}_{n}}}} —(1)
Or \displaystyle {{\vec{r}}_{{cm}}}=\sum{{\frac{{{{m}_{i}}{{{\vec{r}}}_{i}}}}{M}}}
where \overrightarrow{{{{r}_{1}}}}={{x}_{i}}\hat{i}+{{y}_{i}}\hat{j}+{{z}_{i}}\hat{k}. and {{\overrightarrow{{r\,}}}_{{\mathbf{CM}}}}={{x}_{{\mathbf{CM}}}}\,\hat{i}+\ {{y}_{{\mathbf{CM}}}}\,\hat{j}+{{z}_{{\mathbf{CM}}}}\,\hat{k}.
where M = ∑mi is the total mass of the system.
The components ofequation (1) are defined as
{{x}_{{\mathbf{CM}}}}=\frac{1}{M}\sum\limits_{{i=1}}^{n}{{{{m}_{i}}{{x}_{i}}}},\ \,\,{{y}_{{\mathbf{CM}}}}=\frac{1}{M}\sum\limits_{{i=1}}^{n}{{{{m}_{i}}{{y}_{i}}}},\ \,{{z}_{{\mathbf{CM}}}}=\frac{1}{M}\sum\limits_{{i=1}}^{n}{{{{m}_{i}}{{z}_{i}}}},
For locating center of mass of a continuous distribution of mass like 3D bodies etc.
We can write, {{x}_{{\mathbf{CM}}}}=\frac{1}{M}\int{{x\,dm}} , {{y}_{{\mathbf{CM}}}}=\frac{1}{M}\int{{y\,dm}} , {{z}_{{\mathbf{CM}}}}=\frac{1}{M}\int{{z\,dm}}
For derivation part please see the video lectures
Certain Important Points Related To Centre of mass
(1)
There may or may not be any mass present physically at centre of mass.
(2)
It may be within or outside the body.
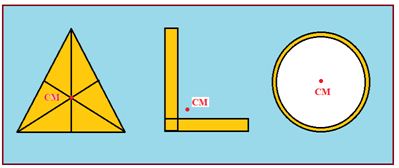
(3)
Its position depends on the shape of the body.
(4)
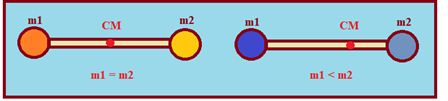
For a given shape it depends on the distribution of mass within the body and is closer to massive part.
(5)
For symmetrical bodies having homogeneous distribution of mass it coincides with centre of symmetry or geometrical centre.
Symmetry can give an idea to locate the position of center of mass
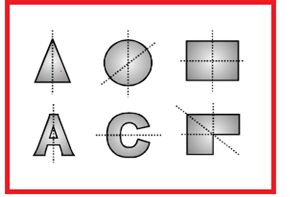
The center of mass of the above sheets will lie on the dotted line shown.
(6)
If we know the centre of mass of parts of the system and their masses, we can get the combined centre of mass by treating the parts as point particles placed at their respective centre of masses.
(7)
It is independent of the co-ordinate system, e.g., the centre of mass, i.e., {{\overrightarrow{{R\,}}}_{{CM}}}=0, then by definition (1/M)\sum{{{{m}_{i}}}}\,\overrightarrow{{{{r}_{i}}}}=0 or \sum{{{{m}_{i}}}}\,\overrightarrow{{{{r}_{i}}}}=0 .
i.e., the sum of the moments of the masses of a system about its centre of mass is always zero.
Are centre of mass and centre of gravity, two words for one and the same point?
No, centre of mass of a body is defined as the point at which the whole of its mass is supposed to be concentrated while centre of gravity of a body is defined as the point at which whole of its weight is supposed to be concentrated.
Illustration
Calculate the position of centre of mass of a system consisting of two particles of masses m1 and m2 separated by a distance L apart, from m1.
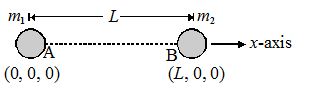
Solution
Treating the line joining the two particles as x-axis, and m1 at the origin, the co-ordinates of the two particles will be (0, 0, 0) and (L, 0, 0). So,
{{X}_{{CM}}}=\frac{{{{m}_{1}}\times 0+{{m}_{2}}L}}{{{{m}_{1}}+{{m}_{2}}}};\ \,\,\,{{X}_{{CM}}}=\frac{{{{m}_{1}}\times 0+{{m}_{2}}\times 0}}{{{{m}_{1}}+{{m}_{2}}}}\ \,\,\,\text{and}\ \,\,{{Z}_{{CM}}}=\frac{{{{m}_{1}}\times 0+{{m}_{2}}\times 0}}{{{{m}_{1}}+{{m}_{2}}}}\
i.e., {{X}_{{CM}}}=\frac{{{{m}_{2}}L}}{{{{m}_{1}}+{{m}_{2}}}};\ {{Y}_{{CM}}}=0\ \,\,\text{and}\ \,\,{{Z}_{{CM}}}=0\
i.e., centre of mass is at a distance [{{m}_{2}}L/({{m}_{1}}+{{m}_{2}})] from m1 internally on the line joining the two particles.
Illustration
The position vectors of three particles of mass m1 = 1 kg, m2 = 2 kg, and m3 = 3 kg are \overrightarrow{{{{r}_{1}}}}=(\hat{i}+4\hat{j}+\hat{k})\mathbf{m},\ \overrightarrow{{{{r}_{2}}}}=(\hat{i}+\hat{j}+\hat{k})\mathbf{m}\ \,\,\text{and}\,\,\ \overrightarrow{{{{r}_{3}}}}=(2\hat{i}-\hat{j}-2\hat{k})\mathbf{m} respectively. Find the position vector of their centre of mass.
Solution:
The position vector of CM of the three particles will be given by
{{\overrightarrow{{r\,}}}_{{CM}}}=\frac{{{{m}_{1}}\overrightarrow{{{{r}_{1}}}}+{{m}_{2}}\overrightarrow{{{{r}_{2}}}}+{{m}_{3}}\overrightarrow{{{{r}_{3}}}}}}{{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}}
Substituting the values, we get
{{\overrightarrow{{r\,}}}_{{CM}}}=\frac{{(1)\ (\hat{i}+4\hat{j}+\hat{k})+(2)(\hat{i}+\hat{j}+\hat{k})+3(2\hat{i}-\hat{j}-2\hat{k})}}{{1+2+3}} =\frac{{9\hat{i}+3\hat{j}-3\hat{k}}}{6}
{{\overrightarrow{{r\,}}}_{{CM}}}=\frac{1}{2}(3\hat{i}+\hat{j}-\hat{k})\text{m}Ans.
Centre of mass of a uniform Rod
Suppose a rod of mass M and length L is lying along the x-axis with its one end at x = 0 and the other at x = L.
Mass per unit length of the rod =\frac{M}{L}
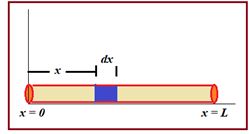
Hence, the mass of the element of length dx situated at x = x is dm=\frac{M}{L}dx
The coordinate of the element of length dx is (x, 0, 0). Therefore, x-coordinate of CM of the rod will be
{{x}_{{CM}}}=\frac{{\int\limits_{0}^{L}{{x\,dm}}}}{{\int{{dm}}}}
=\frac{{\int\limits_{0}^{L}{{(x)\,\left( {\frac{M}{L}dx} \right)}}}}{M}=\frac{1}{L}\int_{0}^{L}{{x\ dx}}=\frac{L}{2}
The y-coordinate of CM is
{{y}_{{CM}}}=\frac{{\int_{{}}^{{}}{{ydm}}}}{{\int_{{}}^{{}}{{dm}}}}=0
(as y = 0)
Similarly, zCM = 0
i.e., the coordinates of CM of the rod are \left( {\frac{L}{2},0,0} \right).
Proceeding in the similar manner, we can find the CM of certain rigid bodies. Centre of mass of some well known rigid bodies are given below:
1.
Centre of mass of a uniform rectangular, square or circular plate lies at their geometrical centre.
2.
Centre of mass of a uniform semicircular ring lies at a distance of h=\frac{{2R}}{\pi } from its centre, on the axis of symmetry where R is the radius of the ring.
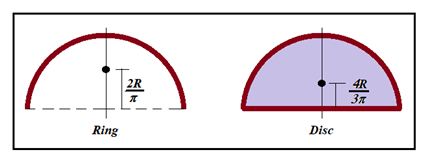
3.
Centre of mass of a uniform semicircular disc of radius R lies at a distance of h=\frac{{4R}}{{3\pi }} from the centre on the axis of symmetry.
4.
Centre of mass of a hemispherical shell of radius R lies at a distance of h=\frac{R}{2} from its centre on the axis of symmetry.
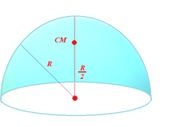
5.
Centre of mass of a Solid hemisphere of radius R lies at a distance of h=\frac{{3R}}{8} from its centre on the axis of symmetry.
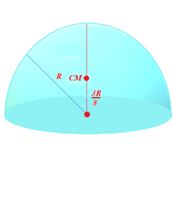
Illustration
Find the position of centre of mass of the uniform lamina shown in figure.
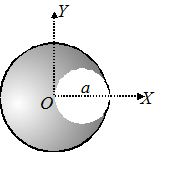
Solution
Here, A1 = area of complete circle =\pi {{a}^{2}}
A2 = area of small circle =\pi \,{{\left( {\frac{a}{2}} \right)}^{2}}=\frac{{\pi {{a}^{2}}}}{4}
(x1, y1) = coordinates of centre of mass of large circle = (0, 0)
and (x2, y2) = coordinates of centre of mass of small circle =\left( {\frac{a}{2},0} \right)
Using {{x}_{{\mathbf{CM}}}}=\frac{{{{A}_{1}}{{x}_{1}}-{{A}_{2}}{{x}_{2}}}}{{{{A}_{1}}-{{A}_{2}}}}
We get {{x}_{{\mathbf{CM}}}}=\frac{{-\frac{{\pi {{a}^{2}}}}{4}\left( {\frac{a}{2}} \right)}}{{\pi {{a}^{2}}-\frac{{\pi {{a}^{2}}}}{4}}}=\frac{{-\left( {\frac{1}{8}} \right)}}{{\left( {\frac{3}{4}} \right)}}a=-\frac{a}{6}
and {{y}_{{\mathbf{CM}}}}=0 as y1 and y2 both are zero.
Therefore, coordinates of CM of the lamina shown in figure are \left( {-\frac{a}{6},0} \right).
Illustration
In the arrangement shown in figure, {{m}_{A}}=2\mathbf{kg} and {{m}_{B}}=1\mathbf{kg} String is light and inextensible. Find the acceleration of centre of mass of both the blocks. Neglect friction everywhere.
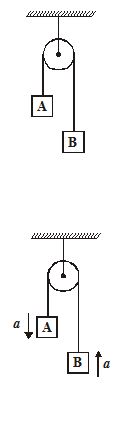
Solution:
Net pulling force on the system is ({{m}_{A}}-{{m}_{B}})g
or, (2-1)g=g
Total mass being pulled is ({{m}_{A}}+{{m}_{B}}) or 3 kg
a=\frac{{\text{Net}\ \text{pulling}\ \text{force}}}{{\text{Total}\ \text{mass}}}=\frac{g}{3}
Now, {{\overrightarrow{{a\,}}}_{{CM}}}=\frac{{{{m}_{A}}\overrightarrow{{{{a}_{A}}}}+{{m}_{B}}\overrightarrow{{{{a}_{B}}}}}}{{{{m}_{A}}+{{m}_{B}}}}
hence \left| {{{{\vec{a}}}_{{cm}}}} \right|=\frac{{(2)(a)-(1)(a)}}{{1+2}}=\frac{a}{3} =\frac{g}{9} downward.
Illustration
Two particles of equal mass have velocity \overrightarrow{{{{v}_{1}}}}=2\hat{i}\,\text{m/s} and \overrightarrow{{{{v}_{2}}}}=2\hat{j}\,\text{m/s}\text{.} First particle has an acceleration \overrightarrow{{{{a}_{1}}}}=(3\hat{i}+3\hat{j})\,\text{m/}{{\text{s}}^{\text{2}}} while the acceleration of the other particle is zero. The centre of mass of the two particles moves on a
(1) circle
(2) parabola
(3) straight line
(4) ellipse
Solution:
{{\overrightarrow{{v\,}}}_{{COM}}}=\frac{{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}} =\frac{{\overrightarrow{{{{v}_{1}}}}+\overrightarrow{{{{v}_{2}}}}}}{2} Q ({{m}_{1}}={{m}_{2}})
=(\hat{i}+\hat{j})\,\text{m/s}
Similarly, {{\overrightarrow{{a\,}}}_{{COM}}}=\frac{{\overrightarrow{{{{a}_{1}}}}+\overrightarrow{{{{a}_{2}}}}}}{2}=\frac{3}{2}(\hat{i}+\hat{j})\,\text{m/}{{\text{s}}^{2}}
Since {{\overrightarrow{{v\,}}}_{{COM}}} is parallel to {{\overrightarrow{{a\,}}}_{{COM}}} the path will be a straight line
(3)
Solution:
The rope tension is the same on both the left and right hand side at every instant, and consequently momentum of both sides are equal
Mv=(M-m)\ (-v)+m({{v}_{r}}-v)
or v=\frac{m}{{2M}}{{v}_{r}}
Momentum of the centre of mass is P={{P}_{1}}+{{P}_{2}}
or {{v}_{{COM}}}=v=\frac{m}{{2M}}{{v}_{r}}
(2).
Illustration
Masses \text{8, 2, 4, 2 }kg\text{ } are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80\,cm. The distance of centre of mass from A will be
(a) 20\,cm
(b) 30\,cm
(c) 40\,cm
(d) 60\,cm
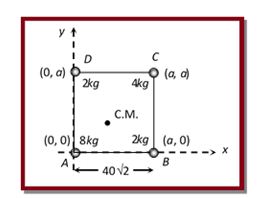
Solution :
Let corner A of square ABCD is at the origin and the mass 8 kg is placed at this corner (given in problem) Diagonal of square d=a\sqrt{2}=80\,cm a=40\sqrt{2}cm
{{m}_{1}}=8kg,\, {{m}_{2}}=2kg, {{m}_{3}}=4kg, {{m}_{4}}=2kg
Let {{\overrightarrow{{\,r}}}_{1}},\,{{\overrightarrow{{\,r}}}_{2}},\,{{\overrightarrow{{\,r}}}_{3}},\,{{\overrightarrow{{\,r}}}_{4}} are the position vectors of respective masses
{{\overrightarrow{{\,r}}}_{1}}=0\hat{i}+0\hat{j}, \overrightarrow{{{{r}_{2}}}}=a\hat{i}+0\hat{j} , \overrightarrow{{{{r}_{3}}}}=a\hat{i}+a\hat{j} , \overrightarrow{{{{r}_{4}}}}=0\hat{i}+a\hat{j}
From the formula of centre of mass
\overrightarrow{{r\,}}=\frac{{{{m}_{1}}\overrightarrow{{{{r}_{1}}}}+{{m}_{2}}\overrightarrow{{{{r}_{2}}}}+{{m}_{3}}\overrightarrow{{{{r}_{3}}}}+{{m}_{4}}\overrightarrow{{{{r}_{4}}}}}}{{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}} =15\sqrt{2}i+15\sqrt{2}\hat{j}
co-ordinates of centre of mass =(15\sqrt{2},\,15\sqrt{2}) and co-ordination of the corner =[0,0]
From the formula of distance between two points ({{x}_{1}},\,\,{{y}_{1}}) and ({{x}_{2}},\,{{y}_{2}})
distance =\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}} = \sqrt{{{{{(15\sqrt{2}-0)}}^{2}}+{{{(15\sqrt{2}-0)}}^{2}}}} = \sqrt{{900}} = 30cm
(b)
Illustration
The coordinates of the positions of particles of mass 7,\,4\text{ and 10}\,gm are \text{(1,}\,\text{5,}\,-\text{3),}\,\,\text{(2,}\,5,7\text{) } and \text{(3, 3, }-\text{1)}\,cm respectively. The position of the centre of mass of the system would be
(a) \left( {-\frac{{15}}{7},\frac{{85}}{{17}},\frac{1}{7}} \right)\text{ }cm
(b) \left( {\frac{{15}}{7},-\frac{{85}}{{17}},\frac{1}{7}} \right)\text{ }cm
(c) \left( {\frac{{15}}{7},\frac{{85}}{{21}},-\frac{1}{7}} \right)\text{ }cm
(d) \left( {\frac{{15}}{7},\frac{{85}}{{21}},\frac{7}{3}} \right)\text{ }cm
Solution: (c)
{{m}_{1}}=7gm , {{m}_{2}}=4gm , {{m}_{3}}=10gm
and \overrightarrow{{{{r}_{1}}}}=(\hat{i}+5\hat{j}-3\hat{k}),\,\,{{r}_{2}}=(2i+5j+7k), {{r}_{3}}=(3\hat{i}+3\hat{j}-\hat{k})
Position vector of center mass \overrightarrow{{\,r}}=\frac{{7(\hat{i}+5\hat{j}-3\hat{k})+4(2\hat{i}+5\hat{j}+7\hat{k})+10(3\hat{i}+3\hat{j}-\hat{k})}}{{7+4+10}}
=\frac{{(45\hat{i}+85\hat{j}-3\hat{k})}}{{21}}
\overrightarrow{{r\,}}=\frac{{15}}{7}\hat{i}+\frac{{85}}{{21}}\hat{j}-\frac{1}{7}\hat{k}
.So coordinates of centre of mass \left[ {\frac{{15}}{7},\,\frac{{85}}{{21}},\,\frac{{-1}}{7}} \right].
Objective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
