Video Lecture
Theory For Notes Making
Concept Of Potential
\displaystyle dW={{\vec{F}}_{{ext}}}.\overrightarrow{{ds}}
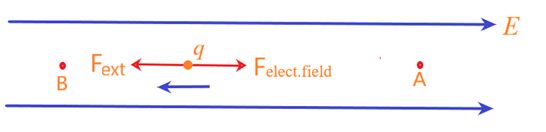
Let us take a test charge q from a point A to another point B with constant speed in an electrostatic field E .When the charge is taken in an electric field two forces are acting on it one is of electrostatic field (F=qE) and other of external agent (Fext) and both do work on the charge. Now to keep the speed constant, it is necessary that the change in kinetic energy of the charge should be zero. From the equation of Work energy theorem we know that
\displaystyle {{W}_{{total}}}=\Delta KE
\displaystyle \Rightarrow {{W}_{{ext}}}+{{W}_{{elect.field}}}=0\text{ (}\Delta KE\text{ is zero)}
\displaystyle \Rightarrow {{W}_{{ext}}}=-{{W}_{{elect.field}}}
Hence it should be noted that the force of external agent should be opposite to that of electrostatic field i.e. Fext = – (qE).
In other words the external agent is doing work against the electrostatic force which is conservative in nature. And we know that work done against a conservative force changes the potential energy of the system (here the potential energy of the test charge).
Therefore we can write \displaystyle {{W}_{{ext}}}=\Delta PE ——(i)
Important Point To Understand is that when our test charge is a unit positive charge we replace the Potential energy (PE) with a simple word Potential and denote it with V. Hence Potential is nothing but the potential energy of a unit positive charge or we can say that the potential is the potential energy per unit charge.
Hence \displaystyle V=\frac{{PE}}{q}
Or \displaystyle PE=Vq ——(ii)
Some author use symbol U for potential energy then we can write the above equation as \displaystyle U=Vq
Also understand that potential is produced by the field and it has nothing to do with the charge to be carried. It is the potential energy which depends on the magnitude of the charge as given in equation (ii)
This concept is similar to that of electric field intensity and electrostatic force. Recall that electric field intensity is nothing but the electrostatic force acting on a unit positive charge or simply it is the force per unit charge so we write \displaystyle \vec{E}=\frac{{\vec{F}}}{q}.
The potential at a point is represented by symbol V. Its S.I. unit is volt. ( 1 volt = 1 J/C ).The dimensions of V are
\displaystyle \text{ }\!\![\!\!\text{ }V] = \left[ {\frac{{PE}}{q}} \right] =\text{ }\left[ {\frac{{\text{M}{{\text{L}}^{\text{2}}}{{\text{T}}^{{-2}}}}}{{\text{AT}}}} \right]\text{ }=\text{ }\left[ {\text{M}{{\text{L}}^{\text{2}}}{{\text{T}}^{{-3}}}{{\text{A}}^{{-1}}}} \right]
Now let the external work is Wext . This work is related with potential energy because it is done against the conservative electrostatic field
If VA and VB are the electric potentials of two points A and B, and if we are moving from point A to B, then potential difference is
ΔV = VB–VA
Once the potential difference between two points is known, the external work needed to move a charge q (with no change in its speed) from point A to B may be found
From equation (i) \displaystyle {{W}_{{ext}}}=\Delta PE
\displaystyle \Rightarrow {{W}_{{ext}}}=P{{E}_{B}}-P{{E}_{A}}
\displaystyle \Rightarrow {{W}_{{ext}}}={{V}_{B}}q-{{V}_{A}}q
\displaystyle \Rightarrow {{W}_{{ext}}}=({{V}_{B}}-{{V}_{A}})q ————(3)
From the above equation we can derive the definition of potential at any point.
If Initial point A is taken at infinity and the potential at infinity is taken as zero (conventionally) and the test charge q is taken as a unit positive charge, then we can put VA=0 and q=1 in the above equation number (3)
we get \displaystyle \Rightarrow {{W}_{{ext}}}=({{V}_{B}}-0)\times 1
hence \displaystyle {{W}_{{ext}}}={{V}_{B}} . Therefore the potential at a point (in an electric field) is the external work needed to bring a positive unit charge, at constant speed, from the position of zero potential to the given point. Conventionally, the point of zero potential is taken at infinity.
Importance Of Sign Of Work
As we know that \displaystyle {{W}_{{ext}}}=({{V}_{B}}-{{V}_{A}})=\Delta V.q
From the above relation it is clear that the sign of this work depends on the sign of q and the relative magnitudes of VA and VB.
(i)
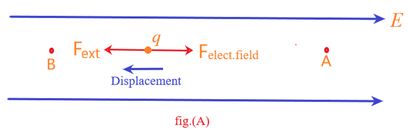
If Wext> 0, that is work is positive :
Work is done by the external agent on the charge as shown in fig.(A) where the charge is displaced opposite to the electric field. In this case the potential energy of the charge increases
(ii)
If Wext< 0, that is work is negative:
Work is done by the field. In this case, the external force acts opposite to the displacement of the charge and the charge is displaced along the electric field. In this case the potential energy of the charge decreases.
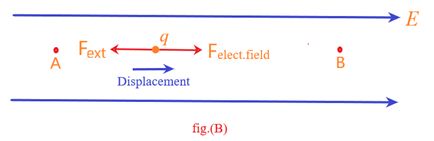
The quantity ΔV depends only on the field set up by the source charges, not on the test charge.
Potential of a Point Charge
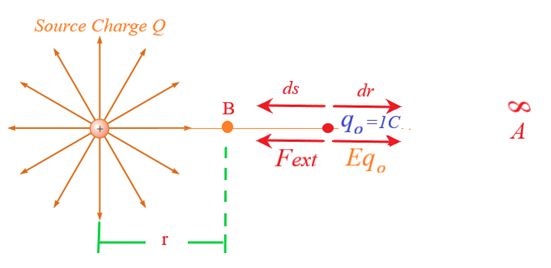
∞∞Consider a test charge qo=1C to be taken from infinity (A) to a point B in the electric field of a source charge Q. At any point in between A and B the electric field due to the source point charge Q is given as
\displaystyle \vec{E}=\frac{{kQ}}{{{{r}^{2}}}}\hat{r}
Let the test charge is given a displacement ds for which the work done by the external force is
\displaystyle dW={{\vec{F}}_{{ext}}}.\overrightarrow{{ds}}
\displaystyle \Rightarrow dW=-{{q}_{o}}E\times (-dr)\cos ({{180}^{o}}) hereqo = 1
\displaystyle \Rightarrow dW=-E\times dr [becausedW=dV ( potential difference)]
\displaystyle \Rightarrow dV=-E\times dr ———-(4)
The change in potential from point A to point B is
\int\limits_{{{{V}_{A}}}}^{{{{V}_{B}}}}{{dV}}=-\int_{A}^{B}{{E\text{ }dr}}=-\int_{A}^{B}{{\frac{{kQ}}{{{{r}^{2}}}}d}}r
\Rightarrow {{V}_{B}}-{{V}_{A}}=-kQ\int_{A}^{B}{{\frac{{dr}}{{{{r}^{2}}}}}}
\Rightarrow {{V}_{B}}-{{V}_{A}}=-kQ\left[ {-\frac{1}{r}} \right]_{\text{A}}^{\text{B}}=\text{ }kQ\text{ }\left( {\frac{1}{{{{r}_{\text{B}}}}}-\frac{1}{{{{r}_{\text{A}}}}}} \right)
If we choose V = 0 at r = ∞ that is at A, the point A shift to the infinity. The potential at any point B radially at a distance r from the source charge in the field is given as
V=\frac{{kQ}}{r}
Potential of a System of Charges
The principle of superposition is also applicable for potentials. The total potential at a point is given by the algebraic sum of the potentials due to the individual charges,
V = V1 + V2 + V3 + …
Figure shows the potential of two equal and opposite point charges separated by a distance. The dotted curves are the individual potential functions, whereas the solid curve is the total potential function. Notice that at the mid-point, V = 0 but E ≠ 0.
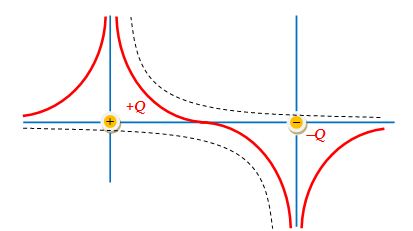
Figure: Potential variation of two equal but opposite charges separated by some distance
Figure shows the total potential due to two equal positive point charges separated by a distance. Notice that at the mid-point E = 0 by V ≠ 0.
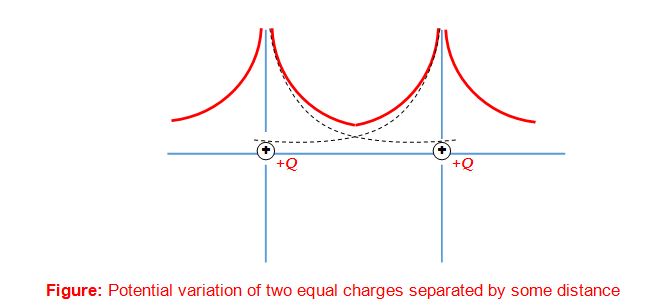
Potential Due to a Continuous Charge Distribution
The potential due to a continuous charge distribution may be obtained in two ways.
First method
Find the potential at the given point (see figure) due to an infinitesimally small point charge dq.
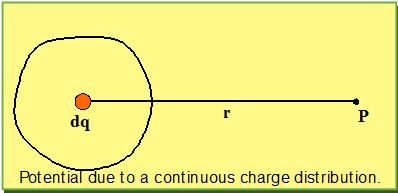
That is dV = \frac{{kdq}}{r}
Integrate this expression over the whole charge distribution
V = k \int{{\frac{{dq}}{r}}}
Second method
If E is already known by, Gauss law, then potential may be obtained from equation
VB– VA = -\int\limits_{A}^{B}{{E.ds}}

Line Integral of electric field
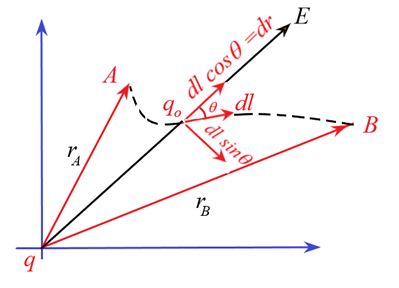
Consider a source charge placed at the origin. Let a test charge qo is to be taken from A to B along any curved path shown by the dotted black curve in the diagram. At any point between A and B the charge qo is present where the electric field due to source charge is E. The force on the test charge is qoE at this point.Let the test charge is given a small displacement dl here. Now dl can be resolved into two components one along the force or electric field i.e. dlcosq and other perpendicular to field i.e. dlsinq. Since dlsinq is perpendicular to the force or field so no work is done for this component of displacement. Hence all work is to be done for dl cosq component. This component is called the radial component and denoted by dr.
We know that electrostatic force is \vec{F}={{q}_{o}}\vec{E}.
The work done by this force is dW=\vec{F}.\overrightarrow{{dl}}={{q}_{o}}\vec{E}.\overrightarrow{{dl}}
Hence \frac{{dW}}{{{{q}_{o}}}}=\vec{E}.\overrightarrow{{dl}}
total work done from A to B can be found by integration
\displaystyle \frac{1}{{{{q}_{o}}}}\int\limits_{A}^{B}{{dW}}=\int\limits_{A}^{B}{{\vec{E}.\overrightarrow{{dl}}}}
\displaystyle \Rightarrow \frac{W}{{{{q}_{o}}}}=\int\limits_{A}^{B}{{\vec{E}.\overrightarrow{{dl}}}}
In the above equation the integration of electric field i.e. \displaystyle \int\limits_{A}^{B}{{\vec{E}.\overrightarrow{{dl}}}} gives the Line Integral Of Electric Field.
It is defined as the work done by the electric field in displacing a unit positive charge from one point to other in an electric field.
In this case when the source charge is a point charge we can calculate the line integral as follows \displaystyle \int\limits_{A}^{B}{{\vec{E}.\overrightarrow{{dl}}}}=\int\limits_{A}^{B}{{E.dl\cos \theta }}
\displaystyle =\int\limits_{{{{r}_{A}}}}^{{{{r}_{B}}}}{{E.dr}} ( \displaystyle \because dlcosq =dr)
\displaystyle \Rightarrow \int\limits_{{{{r}_{A}}}}^{{{{r}_{B}}}}{{E.dr}}=kq\int\limits_{{{{r}_{A}}}}^{{{{r}_{B}}}}{{\frac{{dr}}{{{{r}^{2}}}}}}=kq\left[ {-\frac{1}{r}} \right]_{{{{r}_{A}}}}^{{{{r}_{B}}}}
\displaystyle \Rightarrow \int\limits_{{{{r}_{A}}}}^{{{{r}_{B}}}}{{E.dr}}=-kq\left[ {\frac{1}{{{{r}_{B}}}}-\frac{1}{{{{r}_{A}}}}} \right]=kq\left[ {\frac{1}{{{{r}_{A}}}}-\frac{1}{{{{r}_{B}}}}} \right]
The final value of line integral which was actually work done on a unit positive charge depends only on initial and final position vectors i.e. rA and rB only and not on the path taken between A and B, so we can
Relationship between E and V
We know that
ΔV = \frac{{{{W}_{{ext}}}}}{q}
Also Wext= \int{{{{{\vec{F}}}_{{ext}}}.d\overrightarrow{l}}}
Since the external force is equal and opposite to the electrostatic force
Therefore, {{\vec{F}}_{{ext}}}=-q\vec{E}
or Wext= – \int{{q\,\vec{E} .\,\overrightarrow{{d\,l}}}}
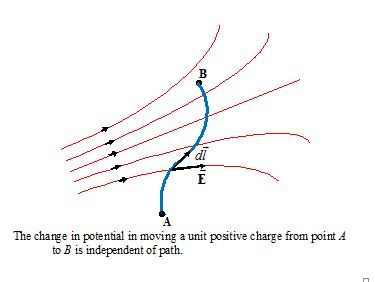
The figure shows a curved path in a non-uniform field. The potential difference between the points A and B is given by
VB –VA= -\int\limits_{A}^{B}{{\vec{E}.\overrightarrow{{dl}}}} (5)
Since the electrostatic field is conservative the value of this line integral depends only on the end points A and B, not on the path taken.
The equation (5) can be used to find the potential function if electric field function is given. Let us see, how to obtain an expression for electric field if potential function is known?
An infinitesimal change in potential associated with the displacement d \vec{s} is given by
dV = – \vec{E}.d \vec{l} = –Edlcosθ
Since Es= E cosθ is the component of \vec{E} along d \vec{l} , the above equation may be written as
dV = –Esdl, from which we infer that
Es= – \frac{{dV}}{{dl}} (6)
Since the direction of d \vec{l} is arbitrary, equation (6) may be interpreted as follows:
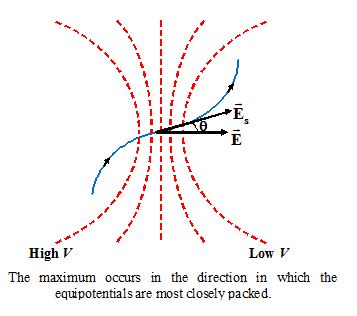
Any component of \vec{E} may be found from the rate of V with distance in the chosen direction. There will be one direction for which this rate of change is a maximum. The magnitude of \vec{E} is given by this maximum value of the spatial derivative: that is E = -(dV/dl)max. As figure given belowshows, the maximum occurs in the direction in which the equipotentials are most closely spaced.
In rectangular components the electric field is
\vec{E}= Ex \hat{i} + Ey \hat{j} + Ez \hat{k}and an infinitesimal displacement is
d \vec{l}= dx \hat{i} + dy \hat{j} + dz \hat{k} . Thus,
dV= – \vec{E}. d \vec{l}
dV = -(Exdx + Eydy + Ezdz) (14)
For a displacement in the x direction,
dy = dz= 0
and so dV= –Exdx.
Therefore,
Ex= -{{\left( {\frac{{dV}}{{dx}}} \right)}_{{y,z\,\text{cons}\tan t}}}
A derivative in which all variables except one are held constant is called partial derivative and is written with a ∂ instead of d. The electric field is therefore
\vec{E} = -\frac{{\partial V}}{{\partial x}}\,\hat{i}\,-\frac{{\partial V}}{{\partial y}}\hat{j}\,-\frac{{\partial V}}{{\partial z}}\hat{k} (7)
The right side of equation (7) is called the gradient of V.
Illustration
If in figure, q = 40 µC, x = 0.5m, y = 0.8m, z = 0.6m, what is the potential at point P?
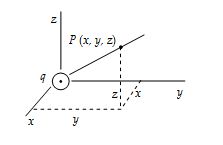
Solution
Here r = (0.52 + 0.82 + 0.62)1/2 = 1.118m. Hence,
\displaystyle {{V}_{P}}=k\frac{q}{r}=(9\times {{10}^{9}})\frac{{40\times {{{10}}^{{-6}}}}}{{1.118}}=3.22\times {{10}^{5}}\text{V}\,\,\text{=}\,\,\text{322kV}
Illustration
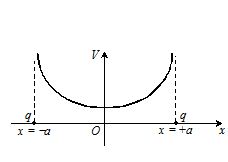
Two identical positive point charges q are placed on the
x-axis at x=-a and x=+a , as shown in figure.
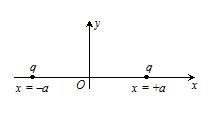
(i) Plot the variation of V along the x-axis.
(ii) Plot the variation of V along the y-axis.
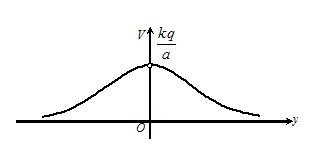
V=\frac{{kq}}{{\sqrt{{{{a}^{2}}+{{y}^{2}}}}}}
\frac{{dV}}{{dy}}=\frac{{-kqy}}{{{{{\left( {{{a}^{2}}+{{y}^{2}}} \right)}}^{{3/2}}}}}
{{V}_{{\max }}} occurs at y=0
And its value is {{V}_{{\max }}}=\frac{{kq}}{a}
Illustration
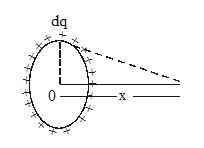
What is the electric potential on the axis of a uniformly charged ring of radius R containing charge q, at a point x away from the center of the loop?
Solution
Let us consider a charge element ‘dq’ on the ring. Now electric potential due to this charge element at P is given by
\displaystyle dV\,\,=\,\,\frac{{dq}}{{4\pi {{\varepsilon }_{0}}\,\,\sqrt{{{{R}^{2}}+{{x}^{2}}}}}}
As electric potential is a scalar quantity. Hence electric potential at P.
\displaystyle V\,\,=\,\,\int{{\frac{1}{{4\pi {{\varepsilon }_{0}}}}}}\,\,\,\,\frac{{dq}}{{\sqrt{{{{R}^{2}}+{{x}^{2}}}}}}\,\,\,=\,\,\,\,\frac{1}{{4\pi {{\varepsilon }_{0}}\sqrt{{{{R}^{2}}+{{x}^{2}}}}}}\,\,\,\int{{dq}}
or \displaystyle V\,\,=\,\,\frac{q}{{4\pi {{\varepsilon }_{0}}\,\,\sqrt{{{{R}^{2}}+{{x}^{2}}}}}}
Illustration
Two identical thin rings each of radius R are placed coaxially a distance R apart. If {{Q}_{1}} and {{Q}_{2}} are respectively the charges uniformly distributed on the two rings. Find the work done in moving a charge q from the center of one ring to that of the other?
Solution
Let the particle has been moved from center A of ring (charge {{Q}_{1}}) to center B of the ring (charge {{Q}_{2}}) by external agent. Hence work done,
W=q\left( {{{V}_{B}}-{{V}_{A}}} \right)
Here {{V}_{B}}=\frac{{k{{Q}_{1}}}}{{\sqrt{2}R}}+\frac{{k{{Q}_{2}}}}{R}
and {{V}_{A}}=\frac{{k{{Q}_{2}}}}{{\sqrt{2}R}}+\frac{{k{{Q}_{1}}}}{R}
W=kq\,\left[ {\frac{{{{\text{Q}}_{\text{1}}}}}{{\sqrt{\text{2}}R}}+\frac{{{{\text{Q}}_{\text{2}}}}}{R}-\frac{{{{\text{Q}}_{\text{2}}}}}{{\sqrt{\text{2}}R}}-\frac{{{{\text{Q}}_{\text{1}}}}}{R}} \right]
=\frac{{kq}}{R}({{Q}_{1}}-{{Q}_{2}})\left[ {\frac{1}{{\sqrt{2}}}-1} \right]
=\frac{{kq}}{R}({{Q}_{2}}-{{Q}_{1}})\left[ {\frac{{\sqrt{2}-1}}{{\sqrt{2}}}} \right]
POTENTIAL ENERGY OF POINT CHARGES
Consider a point charge q placed at position where the potential is V. The potential energy associated with the interaction of this single charge with the charges that created V is
U = qV (6)
If the source of the potential is a point charge Q, the potential at a distance r from Q is
V = kQ/r. Therefore, the potential energy shared by two charges q and Q separated by r is
U = \frac{{kqQ}}{r} (7)
Implicit in Equation (7)is the choice U = 0 at r= ¥, which allows the following interpretation.
The potential energy of the system of two charges is the external work needed to bring the charges from infinity to the separation r without a change in kinetic energy.
When both charges have the same sign, their potential energy is positive: Positive work is needed to reduce their separation against their mutual repulsion. When the charges have opposite signs, the external work is negative. In this case, the external force has to prevent the particles from speeding up–which means that the external force is directed opposite to the displacement. Negative potential energy means that external work is required to separate the charges.
When calculating the total potential energy of a system of several charges, it is better to write equation (7) as
Uij= \frac{{k{{q}_{i}}{{q}_{j}}}}{{{{r}_{{ij}}}}}
This form helps us not to double count the contributions of the charges.
Note that Uij= Uji and that we do not include terms for which \hat{i} = \hat{j}. Since the potentials obey the principle of linear superposition the total potential energy of a system is simply an algebraic sum and does not depend on how the charges are assembled.
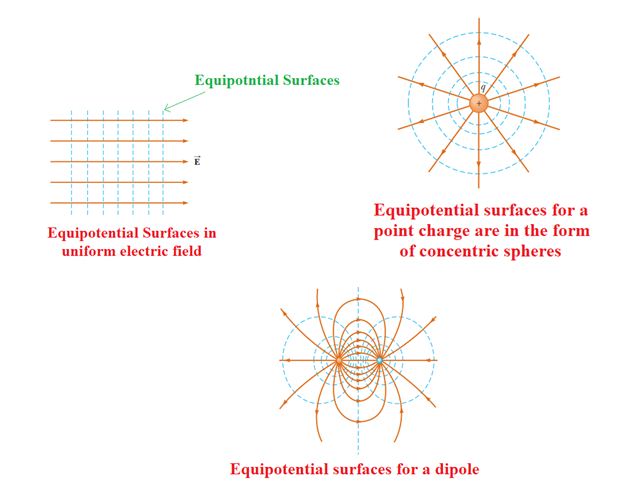
Equipotential Surface
The locus of all the points, which have the same electric potential, is called an equipotential surface, or equipotential line.
Note that
(a)
Equipotential surfaces or lines can never cross each other (otherwise potential at a pointwill have two values which is absurd).
(b)
Equipotential surfaces are always perpendicular to lines of force.
(c)
If a charge is moved from one point to the other over an equipotential surface, work done will be zero.
If the source of the field is a point charge [Fig. (A)] the equipotential surfaces will constitute a family of concentric spheres with their centre at the point where the charge is located.
It is a normal practice to draw equipotential surfaces in such a way that the P.D. (Potential Difference) between two neighboring surfaces be the same. Then the density of equipotential surfaces usually indicates the magnitude of \displaystyle \vec{E} at different points.
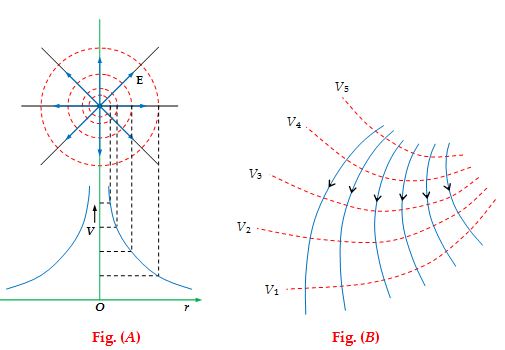
In the figure(A) & (B) the equipotentials are drawn as dashed circles. The solid radial lines represent the field lines. Near the charge, the potential changes rapidly with distance. So the equipotentials are close together. The field lines are always normal to the equipotentials and point toward lower values of potential. The field is strong where the equipotentials are closely spaced.
Fig. (B) shows a two-dimensional pattern of an electrostatic field. The dashes lines correspond to equipotential surfaces; while the solid lines to the lines of \displaystyle \vec{E} . Such a representation immediately shows the direction of vector \displaystyle \vec{E}, the regions where field intensity is higher, as well as the regions with greater steepness of potential change. Obviously, as the field points lower potentials,
V5>V4>V3>V2>V1.
Equipotential surfaces in some cases:
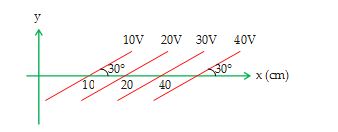
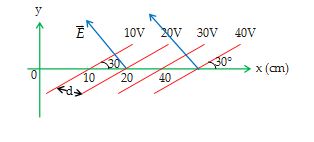
Illustration
The figure shown below represents equipotential surfaces. What can you say about the magnitude and direction of the electric field.
Solution
Since electric field is perpendicular to the equipotential surface and in the direction of decreasing potential, therefore, we can say that electric field will be directed at angle 120º with the +ve x-axis.
Also \displaystyle E\,\,=\,\,-\frac{{dV}}{{dr}}
\displaystyle E\,\,=\,\,\frac{{20-10}}{d}\,\,\,=\,\,\,\frac{{10}}{{10\,\,\sin \,\,30{}^\text{o}}}
= 200 V/m
Objective Assignment
Q.1
What is the potential at the point midway between charges of + 2µC and + 5µC which are 6m apart?
(a) Zero
(b) 21 kV
(c) 10kV
(d) 50kV
Ans: (b)
Q.2
It requires 50 µJ of work to carry a 2 µC charge from point R to S. What is the potential difference between the points? Which point is at the higher potential?
(a) 25V
(b) 10V
(c) 20 V
(d) none
Ans: (a)
Q.3
A point charge 20 mC is shifted from infinity to a point P in an electric field with zero acceleration. If the potential of that point is 1000 volt, then
(i) Find out work done by external agent against electric field?
(a) 25mJ
(b) 20 mJ
(c) 10 mJ
(d)none
Ans- (b),
(ii) what is the work done by electric field?
(a)– 20 mJ
(b) 20 mJ
(c) 10mJ
(d)none
Ans – (a),
(iii) If the kinetic energy of charge particle is found increase by 10 mJ when it is brought from infinity to point P then what is the total work done by external agent?
(a) – 20 mJ
(b) 20 mJ
(c) 30 mJ
(d) none
Ans – (c),
(iv) what is the work done by electric field in the part (iii)
(a) – 20 mJ
(b) 20 mJ
(c) 30 mJ
(d)none
Ans- (a)
(v) If a point charge 30 mC is released at rest at point P, then find out its kinetic energy at a large distance?
(a) – 20 mJ
(b) 20 mJ
(c) 30 mJ
(d) none
Ans- (a)
Q.4
A charge +2mC is kept at the origin and another charge of 1mC is to be carried from (2,2) to (6,2). Then the sign of Work done and potential difference
(a) Both work and potential difference are negative
(b) Both work and potential difference are positive
(c) work is positive and potential difference is negative
(d) work is negative and potential difference is positive
Ans; (a)
Q.5
The electron in a hydrogen atom is most probably at a distance r = 5.29 × 10–11m from the proton, which is the nucleus of the atom. Evaluate the electric potential energy U of the atom.
(a) –27.2eV
(b) –45.2eV
(c) –13.6eV
(d) –3.4eV
Ans : (a)
Q.6
When a 2 µC charge is carried from point A to point B, the amount of work done by the electric field is 50 µJ. What is the potential difference and which point is at a higher potential?
(a) 25 V, B
(b) 25 V, A
(c) 20V, B
(d) both are at same potential
Ans : (b)
Q.7
Variation in potential is maximum if one goes
(a) along the line of force
(b) perpendicular to the line of force
(c) in any direction
(d) none of these
Ans : (a)
Q.8
Two point charges Q and –Q/4 placed along the x-axis are separated by a distance r. Take –Q/4 as origin and it is placed at the right of Q. Then the potential is zero
(a) at x = r/3 only
(b) at x = –r/5 only
(c) both at x = r/3 and at x = –r/5
(d) there exist two points on the axis where the electric field is zero
Ans : (c)
Q.9
Four identical charges are placed at the points (1, 0, 0), (0, 1, 0), (–1, 0, 0) and (0, –1, 0). Then,
(a) the potential at the origin is zero
(b) the electric field at the origin is not zero
(c) the potential at all points on the z-axis, other than the origin, is zero
(d) the field at all points on the z-axis, other than the origin, acts along the z-axis
Ans : (d)
Q.10
The work done in taking a unit positive charge from P to A is WA and from P to B is WB. Then
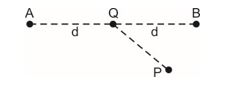
(a) WA > WB
(b) WA < WB
(c) WA = WB
(d) WA + WB = 0
Ans : (c)
Q.11
Three equal charges of +6 nC are located at the corners of an equilateral triangle whose sides are 12 cm long (figure). Find the potential at the centre of the base of the triangle.
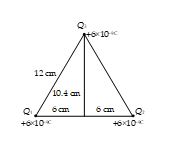
(a) 4500V
(b) 1050V
(c) 2320 V
(d) none
Ans: (c)
12.
Three point charges q, –2q and –2q are placed at the vertices of an equilateral triangle of side a. The work done by some external force to slowly increase their separation to 2a will be
(a) \frac{1}{{4\pi {{\varepsilon }_{0}}}}.\,\,\frac{{2{{q}^{2}}}}{a}
(b) \frac{{{{q}^{2}}}}{{4\pi {{\varepsilon }_{0}}a}}
(c) \frac{1}{{4\pi {{\varepsilon }_{0}}}}.\frac{{3{{q}^{2}}}}{{3R}}
(d) zero
Ans (d)
13.
The electric field intensity at a point at a distance 2 m from a charge q is E. The amount of work done in bringing a charge of 2 coulomb from infinity to this point will be
(a) 2E joules
(b) 4E joules
(c) \frac{E}{2}joules
(d) \frac{E}{4}joules
Ans (b)
14.
Two identical charges are placed at the two corners of an equilateral triangle. The potential energy of the system is U. The work done in bringing an identical charge from infinity to the third vertex is
(a) U
(b) 2U
(c) 3U
(d) 4U
Ans (b)
15.
A unit positive charge has to be brought from infinity to a midpoint between two charges 20mC and 10mC separated by a distance of 50 m. How much work will be required?
(a) 10.8 × 104 J
(b) 10.8 × 103 J
(c) 1.08 × 106 J
(d) 0.54 × 105 J
Ans (b)
16.
Three charges 2q, –q, –q are located at the vertices of an equilateral triangle. At the centre of the triangle
(a) The field is zero but potential is non-zero
(b) The field is non-zero but potential is zero
(c) Both field and potential are zero
(d) Both field and potential are non-zero
Ans (b)
Subjective Assignment
Q.1.
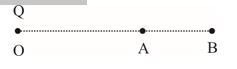
A point charge Q is placed at point O as shown in the figure. Is the potential difference positive, negative or zero, if Q is (i) positive (ii) negative ?
Q.2
Can two equipotential surfaces intersect each other ? Justify your answer.
Q.3
What is the geometrical shape of equipotential surfaces due to a single isolated charge ?
Q.4
Two charges 2 C and –2C are placed at points A and B 5 cm apart. Depict an equipotential surface of the system.
Q.5
For any charge configuration, equipotential surface through a point is normal to the electric field. Justify.
Q.6
What is the electrostatic potential due to an electric dipole at an equatorial point ?
Q.7
What is the work done in moving a test charge q through a distance of 1 cm along the equatorial axis of an electric dipole ?
Q.8
Define the term ‘potential energy’ of charge ‘q’ at a distance ‘r’ in an external electric field.
Q.9
Name the physical quantity whose S.I. unit is JC–1. Is it a scalar or a vector quantity ?
Q.10
A hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. What is the potential at the centre of the sphere ?
Q.11
A regular hexagon of side 10 cm has a charge 5 μC at each of its vertices. Calculate the potential at the centre of the hexagon.
Q.12
(i) Can two equi-potential surfaces intersect each other ? Give reasons.
(ii) Two charges –q and +q are located at points A(0, 0, –a) and B(0, 0, +a) respectively. How much work is done in moving a test charge from point P(7, 0, 0) to Q(–3, 0, 0) ?
Q.13
Draw 3 equipotential surfaces corresponding to a field that uniformly increases in magnitude but remains constant along z-direction. How are these surfaces different from that of a constant electric field along Z-direction ?
Q.14
Write two characteristics of equipotential surfaces
Q.15
Find out the expression for the potential energy of a system of three charges and located respectively at , and with respect to the common origin O.
Q.16
Two uniformly large parallel thin plates having charge densities and are kept in the X-Z plane at a distance ‘d’ apart. Sketch an equipotential surface due to electric field between the plates. If a particle of mass m and charge ‘–q’ remains stationary between the plates, what is the magnitude and direction of this field ?
Q.17
Two point charges 2and –2are placed at points A and B 6 cm apart.
(a) Draw equipotential surfaces of the system.
(b) Why do the equipotential surfaces get closer to each other near the point charges ?
Q.18
Draw a plot showing the variation of (i) electric field (E) and (ii) electric potential (V) with distance r due to a point charge Q.
Q.19
Two charges 5 × 10–8 C and –3 × 10–8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Q.20
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of –2 × 10–9 C from a point P (0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point
R (0, 6 cm, 9 cm).
Q.21
(a) Depict the equipotential surfaces for a system of two identical positive point charges placed a distance ‘d’ apart.
(b) Deduce the expression for the potential energy of a system of two point charges and brought from infinity to the points and respectively in the presence of external electric field .
Q.22
Two tiny spheres carrying charges 1.5 μC and 2.5 μC are located 30 cm apart. Find the potential and electric field:
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
Q.23
In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Å:
(a) Estimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is taken at 1.06 Å separation?
Q.24
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
Q.25
Two charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin whenr/a >> 1.
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
