Video Lecture
Theory For Notes Making
Illustrations
Two electric charges q and -2q are placed at a distance 6 m apart on a horizontal plane. Find the locus of point on this plane where the potential has a value zero.
Solution
Let the charge q is placed at the origin (O) and -2q at (6m, 0m) in the xy-plane. Let the potential at P\,\left( {x,\,\,y} \right) is zero i.e.
\frac{{kq}}{{\sqrt{{{{x}^{2}}+{{y}^{2}}}}}}-\frac{{k\left( {2q} \right)}}{{\sqrt{{{{{(x-6)}}^{2}}+{{y}^{2}}}}}}=0
{{x}^{2}}+{{y}^{2}}=\frac{{{{{(x-6)}}^{2}}+{{y}^{2}}}}{4}
\displaystyle \Rightarrow \,\,{{x}^{2}}\,+\,{{y}^{2}}-4x\,\,=\,12 , \displaystyle {{x}^{2}}-4x+{{4}^{2}}=12+4
\displaystyle {{\left( {x-2} \right)}^{2}}+{{y}^{2}}={{4}^{2}}
After solving we get
Hence the locus of point in the x-y plane where the potential has zero value is a circle of radius 4 m and center (-2, 0) m.
Illustrations
\displaystyle E=20\hat{i}+30\hat{j} exists in space. If the potential at the origin is taken to be zero, find the potential at P (3, 2).
Solution
\displaystyle V={{V}_{x}}+{{v}_{y}}
\displaystyle =\int\limits_{0}^{3}{{-{{E}_{x}}dx}}+\int\limits_{0}^{2}{{-{{E}_{y}}dy}}
\displaystyle =\int\limits_{0}^{3}{{-20\,dx}}+\int\limits_{0}^{2}{{-30dx=-60-60=-120V}}
Ans. (d)
Illustration
Determine the potential energy of the assembly of charges, as shown in figure.
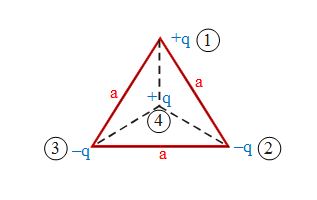
Solution
The potential energy of the assembly of charges is given by
\displaystyle U\,\,\,=\,\,\,\frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\,\,\sum\limits_{{i\,\ne \,j}}^{n}{{\frac{{{{q}_{i}}\,\,{{q}_{j}}}}{{{{r}_{{ij}}}}}}}
or \displaystyle U\,\,\,\,=\,\,({{U}_{{12}}}\,\,+\,\,{{U}_{{13}}}\,\,+\,\,{{U}_{{14}}})\,\,+\,\,({{U}_{{23}}}\,\,+\,\,{{U}_{{24}}})\,\,+\,\,{{U}_{{34}}}
or \displaystyle U\,\,=\,\,-\,\,\frac{{k\,\,{{q}^{2}}}}{a}\,\,=\,\,\frac{{-k{{q}^{2}}}}{a}\,\,+\,\,\frac{{k\,\,{{q}^{2}}}}{{a/\sqrt{3}}}\,\,+\,\,K\,\cdot \,\,\frac{{{{q}^{2}}}}{a}\,\,+\,\,\left( {\frac{{-k\,{{q}^{2}}}}{{a/\sqrt{3}}}} \right)\,\,\,+\,\,\,\left( {\frac{{-k\,\,{{q}^{2}}}}{{a/\sqrt{3}}}} \right)
(where \displaystyle k\,\,=\,\,\frac{1}{{4\pi \,{{\varepsilon }_{0}}}})
or \displaystyle U\,\,=\,\,\frac{{k\,{{q}^{2}}}}{a}\,\,\,\left( {\sqrt{3}+1} \right)\,\,=\,\,\,\,\frac{{{{q}^{2}}\left( {\sqrt{3}+1} \right)}}{{4\pi \,{{\varepsilon }_{0}}\,\,a}}
Illustration
Three point charges q1= 1 µC, q2 = -2µC and q3 = 3 µC are fixed at the positions shown in the figure
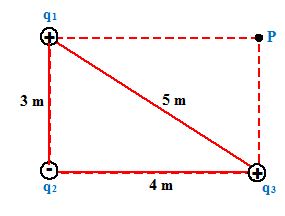
(a) What is the potential at point P at the corner of the rectangle ?
(b) How much work would be needed to bring a charge q4 = 2.5 µC from infinity and to place it at P ?
(c) What is the total potential energy of q1, q2 and q3 ?
Solution
(a)
The total potential at the point P is the scalar sum
VP = V1 + V2 + V3 = \frac{{k{{q}_{1}}}}{{{{r}_{1}}}}\,+\frac{{k{{q}_{2}}}}{{{{r}_{2}}}}\,+\frac{{k{{q}_{3}}}}{{{{r}_{3}}}}
Using the given values
V1 = \frac{{(9.0\,\,\times \,\,{{{10}}^{9}})\,\,({{{10}}^{{-6}}}C)}}{4}\,=2.25\,\,\times \,\,{{10}^{3}}\,V
Similarly, V2 = -3.6 x 103 V and V3 = 9 x 103 V
The total potential is VP = 7.65 x 103 V
(b)
The External work is Wext = q (Vf– Vi). In this case Vi = 0, so
Wext = q4VP = (2.5 x 10–6C) (7.65 x 103 V) = 0.19 J
(c)
The total potential energy of the three charges in the (scalar) sum
U = U12 + U13 + U23 = \frac{{k{{q}_{1}}{{q}_{2}}}}{{{{r}_{{12}}}}}\,+\frac{{k{{q}_{1}}{{q}_{3}}}}{{{{r}_{{13}}}}}\,+\frac{{k{{q}_{2}}{{q}_{3}}}}{{{{r}_{{23}}}}}
We find, for example
U12 = \frac{{(9.0\,\times \,{{{10}}^{9}})\,\,({{{10}}^{{-6}}})\,(-2\,\times \,{{{10}}^{{-6}}})}}{3}\,=\,-6\,\,\times \,\,{{10}^{{-3}}}J
Similarly, U13 = +5.4 X 10–3J and U23 = -13.5 X 10–3 J
The total potential energy is therefore U = -1.41 X 10–2 J
This negative potential energy means that external work is needed to separate the particles and place them at infinity
Illustration
Three point charges q,\,\,2q and 8q are to be placed on a 9 cm long straight line. Find the position where the charges should be placed such that the potential energy of this system is minimum. In this situation, what is the electric field at the position of the charge q due to the other two charges ?
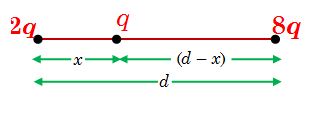
Solution
As potential energy of two point charges separated by a distance r is given by U=\left( {{{q}_{1}}{{q}_{2}}/4\pi {{\varepsilon }_{0}}r} \right) . So, to have minimum potential energy the charges of greater value should be placed farthest, i.e. q must be between 2q and 8q. Let q be at a distance x from 2q, then potential energy of the system will be
U=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left[ {\frac{{2qq}}{x}+\frac{{8qq}}{{(d-x)}}+\frac{{8q\times 2q}}{d}} \right]
For U to be minimum \left( {dU/dx} \right)=0
i.e., -\frac{{2{{q}^{2}}}}{{{{x}^{2}}}}+\frac{{8{{q}^{2}}}}{{{{{(d-x)}}^{2}}}}=0
2x = (d – x) or x = (d/3) = (9/3) = 3 cm
So to have minimum potential energy, the charge q must be placed at a distance of 3 cm from 2q between 2q and 2q, on the line joining the charges.
In this situation field at q\,\,E=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left[ {\frac{{2q}}{{{{{(3)}}^{2}}}}-\frac{{8q}}{{{{{(6)}}^{2}}}}} \right]=0 .
Illustration
A circular ring of radius R with uniform positive charge density l per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P\,\left[ {\sqrt{3}R,\,\,0,\,\,0} \right] on the positive x- axis directly towardsO , with initial speed v. Find the smallest (non zero) value of the speed such that the particle does not return to p.
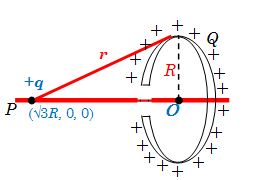
Solution
As the electric field at the centre of a ring is zero, the particle will below is not come back due to repulsion if it crosses the centre, i.e, if the in equality satisfied.
\frac{1}{2}m{{v}^{2}}+\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{qQ}}{r}>\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{qQ}}{R}
For Q=2\pi R\lambda
And r=\sqrt{{{{{(\sqrt{3}R)}}^{2}}+{{R}^{2}}}}=2R , gives
\frac{1}{2}m{{v}^{2}}>\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{2\pi R\,\lambda q}}{R}\left[ {1-\frac{1}{2}} \right]
or v>\sqrt{{\left( {\frac{{\lambda q}}{{2{{\varepsilon }_{0}}m}}} \right)}}
so {{v}_{{\min }}}=\sqrt{{\left( {\frac{{\lambda q}}{{2{{\varepsilon }_{0}}m}}} \right)}}
Objective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
