Video Lecture
Theory For Notes Making
Superposition of waves
If two or more waves arrive simultaneously, the particles of the medium are subjected to two or more simultaneous displacements and hence a new wave is produced. This phenomenon of intermixing of two or more waves to produce a new wave is called superposition of waves.
In case of superposition of waves, the resultant wave functions at any point is the algebraic sum of the wave function of individual waves, i.e.,
y={{y}_{1}}+{{y}_{2}}+{{y}_{3}}+……….
This principle is called principle of superposition.
Interference of waves
It is the phenomena of redistribution of energy of a medium when two waves of same frequency superimpose while moving in the same or almost same direction in that medium. The places where the energy becomes maximum a constructive interference is said to take place whereas the places where resultant energy becomes minimum a destructive interference is said to occur.
Remember that there is no loss or gain of energy of the medium during interference but there is only redistribution.
Let there are two waves {{y}_{1}}={{A}_{1}}\sin (\omega t-kx) and {{y}_{2}}={{A}_{2}}\sin (\omega t-kx+\phi )superimpose at origin where x=0
so According to the principle of superposition
\displaystyle y={{y}_{1}}+{{y}_{2}}
={{A}_{1}}\sin (\omega t)+{{A}_{2}}\sin [\omega t+\phi ] On solving this equation we get the equation of resultant displacement as y=R\sin (\omega t+\theta ){ see video lecture for detailed solution}
where R is resultant amplitude and is given by
R=\sqrt{{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \phi }} and \theta ={{\tan }^{{-1}}}\left[ {\frac{{{{A}_{2}}\sin \varphi }}{{{{A}_{1}}+{{A}_{2}}\cos \varphi }}} \right]</p><p>Resultant Intensity is given by I={{I}_{1}}+{{I}_{2}}+2\sqrt{{{{I}_{1}}}}\,\sqrt{{{{I}_{2}}}}\,\cos \varphi
Condition for Constructive Interference
At the point of constructive interference Intensity will be maximum, which is possible only when cosΦ is maximum i.e. 1 . so
\cos \phi =+1,\,hence\,\,\phi =0,\,\,2\pi ,\,\,\,4\pi ,……2n\pi hence when two waves interfere with a phase difference 2np they produce constructive interference.
Also we know that phase difference \displaystyle \phi =\frac{{2\pi }}{\lambda }(\Delta x)
hence \frac{{2\pi }}{\lambda }\cdot (\Delta x)=2n\pi ,\,\,so\,\,\Delta x=n\lambda
and {{I}_{{\max }}}\,\,={{\left\{ {\sqrt{{{{I}_{1}}}}+\sqrt{{{{I}_{2}}}}} \right\}}^{2}}
Intensity will be maximum at those points where path difference is an even multiple of \lambda /2 and maximum intensity is greater than the algebraic sum of two intensities i.e. ({{I}_{1}}+{{I}_{2}}). These points are called points of constructive interference or interference maxima.
Condition for Destructive Interference
Further, intensity will be minimum where cosΦ is minimum i.e. -1
hence \cos \phi =-1.
therefore \displaystyle \phi =\pi ,\,3\pi ,\,5\pi ,….,(2n-1)\pi
Also we know that phase difference \displaystyle \phi =\frac{{2\pi }}{\lambda }(\Delta x)
hence \frac{{2\pi }}{\lambda }(\Delta x)=(2n-1)\pi ,so\,\,\,\,\Delta x=(2n-1)\frac{\lambda }{2}
{{I}_{{\min }}}={{I}_{1}}+{{I}_{2}}-2\sqrt{{{{I}_{1}}{{I}_{2}}}},\,\,{{I}_{{\min }}}={{(\sqrt{{{{I}_{1}}}}-\sqrt{{{{I}_{2}}}})}^{2}}
Intensity will be minimum at those points where path difference is an odd multiple of \lambda /2 and minimum intensity is lesser than the algebraic sum of two intensities ({{I}_{1}}+{{I}_{2}}). These points are called points of destructive interference.
The diagram given below shows how the intensity varies with phase difference according to relation I={{I}_{1}}+{{I}_{2}}+2\sqrt{{{{I}_{1}}}}\,\sqrt{{{{I}_{2}}}}\,\cos \varphi . The maximum intensity is more than normal algebraic sum ({{I}_{1}}+{{I}_{2}}) by a quantity \displaystyle 2\sqrt{{{{I}_{1}}{{I}_{2}}}}and minimum intensity is less than the algebraic sum ({{I}_{1}}+{{I}_{2}}) by a quantity \displaystyle 2\sqrt{{{{I}_{1}}{{I}_{2}}}}.
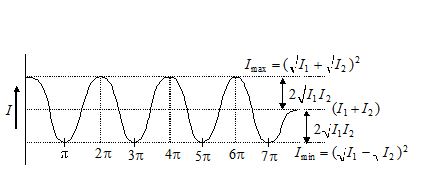
\frac{{{{I}_{{\max }}}}}{{{{I}_{{\min }}}}}=\frac{{{{{\left( {\sqrt{{{{I}_{1}}}}+\sqrt{{{{I}_{2}}}}} \right)}}^{2}}}}{{{{{\left( {\sqrt{{{{I}_{1}}}}-\sqrt{{{{I}_{2}}}}} \right)}}^{2}}}}=\frac{{{{{({{A}_{1}}+{{A}_{2}})}}^{2}}}}{{{{{({{A}_{1}}-{{A}_{2}})}}^{2}}}}\,\,\,\,\,\,\,\mathbf{with}\,\,\,\,\,\,\,\frac{{{{I}_{1}}}}{{{{I}_{2}}}}=\frac{{A_{1}^{2}}}{{A_{2}^{2}}}
Illustration
Two waves having intensity ratio of 100 : 1, interfere with each other. Find the ratio of intensities at the maxima ad minima
Solution:
Ratio of intensities at maxima and minima
\frac{{{{I}_{{\max }}}}}{{{{I}_{{\min }}}}}\,=\,\frac{{{{{({{a}_{1}}+{{a}_{2}})}}^{2}}}}{{{{{({{a}_{1}}-{{a}_{2}})}}^{2}}}}\,\,=\,\,\frac{{{{{(1+\frac{{{{a}_{2}}}}{{{{a}_{1}}}})}}^{2}}}}{{{{{(1-\frac{{{{a}_{2}}}}{{{{a}_{1}}}})}}^{2}}}}
\frac{{{{{(10+11)}}^{2}}}}{{{{{(10-1)}}^{2}}}}= \frac{{121}}{{99}}
Illustration
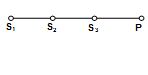
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P? What is minimum value of S1 S2 and S2S3 if the wavelength is l?
Solution:
\displaystyle \frac{{{{S}_{1}}{{S}_{2}}}}{\lambda }2\pi =\frac{{2\pi }}{3}Þ \displaystyle {{S}_{1}}{{S}_{2}}=\frac{\lambda }{3},
\displaystyle \frac{{{{S}_{2}}{{S}_{3}}}}{\lambda }2\pi =\frac{{2\pi }}{3}Þ \displaystyle {{S}_{2}}{{S}_{3}}=\frac{\lambda }{3}.
The amplitude of the resulting sound wave is zero.
Illustration
Two coherent sound sources are at distances x1 = 0.2 m and x2 = 0.48 m from a point. Calculate the intensity of the resultant wave at that point if the frequency of each wave is f = 400 Hz and velocity of wave in the medium is v = 448 m/s. The intensity of each wave is Io = 60 W/m2.
Solution
Path difference, Δx = x2– x1 = 0.48 – 0.2 = 0.28 m
f = \displaystyle \frac{{2\pi }}{\lambda }\Delta x=\left( {\frac{{2\pi f}}{v}} \right)\Delta x=\frac{{2\pi \left( {400} \right)\left( {0.28} \right)}}{{448}}=\frac{\pi }{2}
Now, I = I1 + I2 + 2 \displaystyle \sqrt{{{{I}_{1}}{{I}_{2}}}}cos f
or I = Io + Io + 2Io cos(π/2)
= 2Io = 2(60) = 120 W/m2 .
Illustration
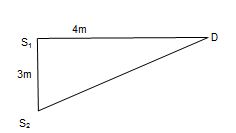
In the figure the intensity of waves arriving at D from two coherent sources s1 and s2 is I0. l = 4 m. What will be the resultant intensity at D?
Solution:
path different e Δx = s2D – s1D = 5 – 4 = 1m
corresponding phase difference will be
Φ= \displaystyle \frac{{2\pi }}{\lambda }.\Delta x=\left( {\frac{{2\pi }}{4}} \right)(1)=\frac{\pi }{2}
Using I = I1 + I2 + 2 \displaystyle \sqrt{{{{I}_{1}}{{I}_{2}}}} cosf
I = I0 + I0 + 2 \displaystyle \sqrt{{{{I}_{1}}{{I}_{2}}}} cos 90 = 2I0.
Illustration
Two waves represented by y1 = 10 Sin (2000 π t) and y2= 10 sin (2000 π t + π/2) are superposed at any point at a particular instant. The resultant amplitude is
(A) 10 units
(B)20 units
(C) 14.1 units
(D) zero
Sol.
The resultant amplitude A of two waves of amplitudes a1 and a2 and phase difference f is ( {{(a_{1}^{2}+a_{2}^{2}+2{{a}_{1}}{{a}_{2}}\cos \varphi )}^{{1/2}}}. Substituting a1 = 10, a2 = 10 and
f = 900, we get A = 14.1.
(C)
Illustration
The wavelength of the sound wave in air is \lambda =\frac{{320}}{{16\times {{{10}}^{3}}}}=2\times {{10}^{{-2}}}m. The positions of maxima on the circumference of the circular track will be given by
d\sin \theta =n\lambda
When d is the separation between the sources and q is the angular position of nth maximum as shown in the figure
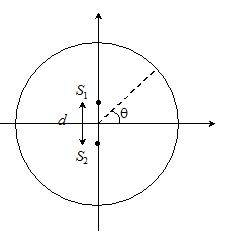
2 sin θ = n (2 x 10-2)
sin θ = \frac{n}{{100}}
Since sin θ lies between 0 and 1 there are 400 maxima on the entire circle.
These 400 maximas will be heard by the person in the time
t=\frac{{400}}{{2beats/s}}=200s
Speed of the train = 36 km/h
=36\times \frac{5}{{18}}=10m/s
From the obtained values so far we get length of track
l = (10 m/s) (200s)= 2000 m
So radius of the track = \frac{{2000}}{{2\pi }} = \frac{{1000}}{\pi }m
Beats:
When two sound waves of nearly equal (but not exactly equal) frequencies travel in same direction at a given point due to their superposition, intensity alternately increases and decreases. This periodic change of sound at a given position is called Beats.
Let us consider two-sound waves of frequencies {{f}_{1}} and {{f}_{2}} propagating simultaneously in a same direction. If we assume that their amplitude are equal at position x=0, then
{{y}_{1}}=a\sin (2\pi {{f}_{1}}t) and {{y}_{2}}=a\sin (2\pi {{f}_{2}}t)
y={{y}_{1}}+{{y}_{2}}=2a\cos \left( {\frac{{2\pi ({{f}_{1}}-{{f}_{2}})t}}{2}} \right)\sin \left( {\frac{{2\pi ({{f}_{1}}+{{f}_{2}})t}}{2}} \right)
Where {{f}_{R}}=\frac{{({{f}_{1}}-{{f}_{2}})}}{2} and {{f}_{{av}}}=\frac{{{{f}_{1}}+{{f}_{2}}}}{2}
y=2a\cos (2\pi {{f}_{{R\,}}}t)\cdot \sin (2\pi \,{{f}_{{av}}}\,t)
Assume 2a\cos (2\pi \,{{f}_{R}}t)=R (Resultant amplitude varies with time t according to a cos function)
y=R\sin (2\pi \,{{f}_{{av}}}.\,t) (Equation of the resultant wave)
For amplitude R to be maximum
i.e., \cos (2\pi \,{{f}_{R}}\cdot t)=\pm 1
i.e., 2\pi \,{{f}_{R}}t=0,\,\pi ,\,2\pi ,……,n\pi
or t=0,\,\,\frac{1}{{2{{f}_{R}}}},\frac{1}{{{{f}_{R}}}},\frac{3}{{2{{f}_{R}}}},….
Time interval between two consecutive maximum intensities is called beat period Tb
{{T}_{b}}={{t}_{n}}-{{t}_{{n-1}}}=\frac{1}{{2{{f}_{R}}}}
Beat frequency, i.e., number of beats per second will be {{\nu }_{b}}=\frac{1}{{{{T}_{b}}}}=2{{f}_{R}}=\frac{{2({{f}_{1}}-{{f}_{2}})}}{2}=({{f}_{1}}-{{f}_{2}})
Thus, beat frequency is equal to the difference of frequencies of two interfering waves.
Illustration
Two tuning forks P and Q, when set in vibration, give 4 beats per second. If a prong of the fork P is filed, the beats are reduced to 2 per second. Determine the frequency of P, if frequency of Q is 250 Hz.
Solution:
There are four beats between P and Q, therefore the possible frequencies of P are 246 or 254 (that is 250 ± 4) Hz.
When the prong of P is filed, its frequency becomes greater than the original frequency.
If we assume that the original frequency of P is 254, then on filing its frequency will be greater than 254. The beats between P and Q will be more than 4. But it is given that the beats are reduced to 2, therefore 254 is not possible.
Thus, the required frequency must be 246 Hz.
(This is true, because on filing the frequency may increase to 248, giving 2 beats with Q of frequency 250 Hz.)
Illustration
Two tuning forks A and B sounded together give 8 beats per second. With an air resonance tube closed at one end, the two forks give resonances when the two air columns are 32 cm and 33 cm respectively. Calculate the frequencies of the forks
Solution:
Let the frequency of the first fork be f1 and that of second be f2 .
We then have,
\displaystyle {{f}_{1}}=\frac{v}{{4\times 32}}and{{f}_{2}}=\frac{v}{{4\times 33}}
We also see that f1 > f2
f1-f2 =8 …(1)
and
\displaystyle \frac{{{{f}_{1}}}}{{{{f}_{2}}}}=\frac{{33}}{{32}} …(2)
Solving (1) and (2), we get
f1 = 264 Hz
and f2 = 256 Hz
Illustration
Two tuning forks A and B produce 4 beats per second when sounded simultaneously. The frequency of A is known to be 256 Hz. When B is loaded with a little wax 4 beats per second are again produced. Find the frequency of B before and after loading.
Solution:
Since the beat frequency is 4 per second, the possible frequencies of fork B before loading are (256 + 4) Hz and (256 – 4) Hz
or 260 Hz and 252 Hz
After loading B with wax, again 4 beats/second are heard. Therefore, after loading, the possible frequencies are
(256 + 4) Hz and (256 – 4) Hz
or 260 Hz and 252 Hz
But, by loading a fork its frequency can only decrease. Hence, before loading fork B, its frequency only be 260 Hz, so that after loading it decreases to 252 Hz.
Objective Assignment
Q.1
Phenomenon of beats can take place
(a) for longitudinal waves only
(b) for transverse waves only
(c) for both longitudinal and transverse
(d) for sound waves only
Ans. (c)
Q.2
Beat are the result of
(a) constructive and destructive interference in time
(b) constructive and destructive interference in space
(c) destructive interference in space
(d) constructive interference in space
Ans. (a)
Q.3
A tuning from produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and number of heats heard are 6 per second. The original frequency of the tuning fork is
(a) 252 Hz (b) 260 Hz (c) 250 Hz (d) 262 Hz
Ans. (a)
Q.4
The number of beats produced per second by two tuning forks when sounded together is 4. One of them has a frequency of 250Hz. The frequency of the other cannot be more than
(a) 252 Hz (b) 254 Hz (c) 246 Hz (d) 248 Hz
Ans. (b)
Q.5
A tuning fork A when sounded together with a fork B of frequency 330 Hz produces
3 beats/sec. When A is loaded with some wax the number of beats per second remains the same. The frequency of A before loading with wax is
(a) 333 Hz (b) 327 Hz (c) 327 or 333 Hz (d) 330 Hz
Ans. (a)
Q.6
Two waves of same frequency but amplitudes equal to a and 2a traveling in the same direction superimpose out of phase. The resultant amplitude will be
(a) \sqrt{{{{a}^{2}}+2{{a}^{2}}}}
(b) 3a
(c) 2a
(d) a
Ans. (d)
Q.7
Two waves each of loudness L superimpose to produce beats. The maximum loudness of the beats will be
(a) 4L (b) 2L (3) L (d) none of these
Ans. (a)
Q.8
Two waves of same frequency but of amplitudes a and 2a respectively superimpose over each other. The intensity at a point where the phase difference is 3\pi /2, will be
(a) a
(b) 3{{a}^{2}}
(c) 5{{a}^{2}}
(d) 9{{a}^{2}}
Ans. (c)
Q.9
What happens when two sound waves of frequencies differing by more than 10 Hz reach our ear simultaneously?
(a) beats are not produced
(b) the waves destroy each other’s effect
(c) interference of sound does not take place
(d) beats are produced but cannot be heard
Ans. (d)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
