Video Lecture
Theory For Notes Making
MECHANICAL WAVE
A wave is a kind of disturbance from the equilibrium condition that propagates without the transport of matter. In general, a wave transports both the energy and the momentum from one point of space to another.
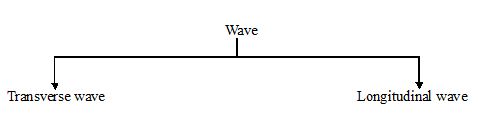
Transverse and longitudinal waves
Two distinct-classes of wave motion are (i) Transverse wave motion (ii) Longitudinal wave motion
In a transverse wave motion, the particles of the medium oscillate about their mean position at right angle to the direction of propagation of wave motion itself.

In a longitudinal wave motion the particles of the medium oscillate about their mean position along the direction of propagation of the wave. This type of wave travels in the form of compression and rarefraction.
The distance between two successive compression or rarefaction constitute one wavelength. Sound waves in a gas are longitudinal in nature while wave in string are transverse.
Equation of a displacement of particles in a harmonic transverse or longitudinal wave
Consider a wave moving along positive direction of x axis as shown in the figure
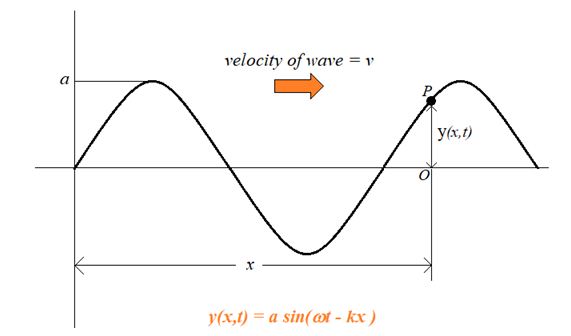
If a traveling wave is a sin or cos function of (ax\pm bt), the wave is said to be harmonic or plane progressive.
Every particle of the medium is oscillating according to an equation y(x,t)=a\sin (\omega t-kx). This equation is called the equation of the wave.( See the video lecture for its derivation )
Here different quantities involved in this equation have physical significance as given below.
Here,
- y(x, t) = displacement of a particle P from its mean position O.
- x = position of the particle
- t = any time
- a = amplitude
- (wt – kx) = phase angle of particle P
- w = angular frequency of wave
- As the phase is (\omega t-kx)= constant, differentiating it with respect to time, we get
\omega -k\left( {\frac{{dx}}{{dt}}} \right)=0\Rightarrow \,\,\omega -k(V)=0
hence V=\frac{\omega }{k} which is wave velocity.
- A plane progressive wave propagating along positive x-axis with x=0 at t=0 is given by y=A\sin (\omega t-kx).
{{V}_{{particle}}}=\frac{{dy}}{{dt}}=A\omega \,\cos (\omega t-kx)
=A\omega \sqrt{{1-{{{\left( {\frac{y}{A}} \right)}}^{2}}}}
=\frac{A}{A}\omega \,\sqrt{{{{A}^{2}}-{{y}^{2}}}}
Particle velocity is maximum where {{y}^{2}}= min =0.
{{({{V}_{{particle}}})}_{{\max }}}=A\omega
Also Slope of the wave is given by \frac{{dy}}{{dx}},so on differentiating the equation of wave we get the slope of the wave.
Hence \frac{{dy}}{{dx}}=-Ak\cos (\omega t-kx).
\frac{{dy}}{{dx}}=-Ak\cdot \frac{{{{V}_{{particle}}}}}{{A\omega }}
{{V}_{{particle}}}=-{{V}_{{wave}}}\times (slope)
Illustration
The equation for the displacement of a stretched string is given by y=4\sin 2\pi \left[ {\frac{t}{{0.02}}-\frac{x}{{100}}} \right]
Where y and x are in cm and t in second. Determine the
(a) direction in which wave is moving (c) time period (e) angular frequency (g) propagation constant (i) phase constant | (b) amplitude (d) frequency (f) wavelength (h) velocity of wave (j) maximum particle velocities. |
Solution:
We will compare the given equation with standard one, which is y=A\sin \,(\omega t\mp kx+\varphi )
y=A\sin \left[ {\frac{{2\pi }}{T}t-\frac{{2\pi }}{\lambda }x+\varphi } \right],\,\,\,\,\,\,\,y=A\sin \,\,2\pi \left[ {\frac{t}{T}-\frac{x}{\lambda }+\varphi } \right]
Clearly,
(a) Wave is propagating along x-axis.
(b) Amplitude =4 cm = 0.04 m
(c) Time period \mathbf{T}=\mathbf{0}\mathbf{.02}\,\mathbf{sec}=\frac{\mathbf{1}}{{\mathbf{50}}}\,\mathbf{sec}
(d) Frequency =\frac{1}{T}=50\,Hz
(e) \omega =2\pi f=100\pi \,\,\mathbf{rad/s}
(f) \lambda =100cm=1\,m
(g) k=\frac{{2\pi }}{\lambda }=2\pi \,rad/m
(h) V=\frac{\omega }{k}=\frac{{100\pi }}{{2\pi }}=50m/s
(i) Phase constant = zero
(j) {{({{V}_{{pa}}})}_{{\max }}}=A\omega =0.04\times 100\pi =4\pi \,m/s
Illustration
An observer standing at seacoast observes 54 waves reaching the coast per minute. If the wavelength of the waves is 10 m, find its velocity.
Solution:
Given: f=\frac{{54}}{{60}}=\frac{9}{{10}}Hz
V=f\lambda =\frac{9}{{10}}\times 10=9\,m/s.
Illustration
A progressive wave of frequency 500 Hz is traveling with a velocity of 360 m/s. How far apart are 2 points 60° out of phase?
Solution:
Since, \lambda =\frac{V}{f}=\frac{{360}}{{500}}=0.72\,m
Now, as in a wave path difference is related to phase difference by the relation, phase difference \varphi =\frac{{2\pi }}{\lambda } (path difference).
Path difference =\frac{{0.72}}{{2\pi }}\times \frac{\pi }{3}=0.12\,m
Illustration
The equation of a transverse wave on a stretched string is given as
y = 2 sin 2p \left\{ {\frac{x}{{30}}\,\,-\,\,\frac{t}{{0.01}}} \right\}
where y and x are cm and t is in s. Find
(a) the amplitude
(b) the frequency
(c) the wavelength, and
(d) the wave velocity
Solution:
(a) Comparing the given equation with the standard equation,
y = A sin (kx – wt) = A sin \left\{ {\frac{{2\pi }}{\lambda }\,x\,-\,\frac{{2\pi }}{T}t} \right\}
= A sin 2 p \left\{ {\frac{x}{\lambda }\,-\,\frac{t}{T}} \right\}
we get
(a) Amplitude A = 2 cm
(b) frequency, = 100 Hz
(c) wave length, l = 30 cm
(d) wave velocity, v = fl= 100 × 30 = 3000 cm/s
= 30 m/s
Illustration
Equation of a transverse wave travelling in a rope is given by
y = 5 sin(4.0t – 0.02x), where y and x are expressed in cm and time in seconds. Calculate
(a) the amplitude, frequency, velocity and wavelength of the wave.
(b) the maximum transverse speed and acceleration of a particle in the rope.
Solution:
(a) Comparing this with the standard equation of wave motion
y = A sin \displaystyle \left( {2\pi ft-\frac{{2\pi }}{\lambda }x} \right)
where A, f and l are amplitude, frequency and wavelength, respectively.
Thus, amplitude A = 5 cm
2pf = 4
Frequency, f = \displaystyle \frac{4}{{2\pi }}=0.637cycle/s
Again, \displaystyle \frac{{2\pi }}{\lambda }=0.02{\leftarrow}\stackrel{\scriptscriptstyle\to}{\leftarrow}Wavelength\,\,(\lambda )=\frac{{2\pi }}{{0.02}}= 100p cm
Velocity of the wave v = \displaystyle f\lambda =\frac{4}{{2\pi }}\frac{{2\pi }}{{0.02}} = 200 cm/s
(b) Transverse velocity of the particle, u = \displaystyle \frac{{\partial y}}{{\partial t}} = 5 x 4 cos(4.0 t – 0.02x)
= 20 cos(4.0 t – 0.02x)
Maximum velocity of the particle = 20 cm/s
Particle acceleration, a = \displaystyle \frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}}=-20\times 4\sin \left( {4.0t-0.02x} \right)
Maximum acceleration of the particle = 80 cm/s2.
Velocity of a Transverse Wave in a Stretched String
The velocity of transverse wave through a string depends on two factors
(i) tension (T) and
(ii) mass per unit length or linear mass density (m) of the string.
Hence \displaystyle V\propto {{\left[ T \right]}^{a}}{{\left[ \mu \right]}^{b}}
now dimensionally we can find that \displaystyle a=\sqrt{{\frac{1}{2}}}\And b=-\sqrt{{\frac{1}{2}}}, replacing the proportionality sign with a constant that comes out to be 1.
Hence final equation for the velocity of wave is
\displaystyle V=\sqrt{{\frac{T}{\mu }}}
Velocity of sound through a medium
When a sound wave travels through a medium such as air, water or steel, then it set particles of the medium into vibrations. For this to happen, the medium must have both inertia and elasticity. These two properties of matter determine the velocity of sound, which is given by
V=\sqrt{{\frac{{\mathbf{Elasticity}\,\,(E)\,}}{{\mathbf{density}\,\,(\rho )}}}} ( This can also be proved dimensionally)
As solids are most elastic than liquids and liquid are more elastic then gases {{E}_{s}}>{{E}_{l}}>{{E}_{g}},
so, velocity of sound is maximum in solids and minimum in gases.
Newton’s Formula for velocity of sound:
Newton suggested that the velocity of the longitudinal waves through any medium depends on the elasticity and density as V=\sqrt{{\frac{E}{\rho }}}.
Since a gas has only one type of elasticity, i.e., bulk modulus (B), the velocity of sound in gases is V=\sqrt{{\frac{B}{\rho }}}.
Newton assumed that the changes in pressure and volume of a gas, when sound waves are propagated through it, are isothermal. The amount of heat produced during compression is lost to the surrounding and similarly the amount of heat absorbed during rarefaction from surrounding, so as to keep the temperature constant.
IF P and V are the initial pressure and volume of the gas.
Then Under Isothermal condition P\mathbf{V}= constant
Differentiating both sides, we get Pd\mathbf{V}+\mathbf{V}dP=0
Pd\mathbf{V}=-\mathbf{V}dP
\,\frac{{-dP}}{{d\mathbf{V/V}}}=P
but, B=-\frac{{dP}}{{(d\mathbf{V}/\mathbf{V})}} (By definition).
P=B
V=\sqrt{{\frac{P}{\rho }}}
If sound wave is passing through air at NTP then V=\sqrt{{\frac{P}{\rho }}}=\sqrt{{\frac{{1.013\times {{{10}}^{5}}}}{{1.29}}}}=280\,\mathbf{m/s}
Experimental value of the velocity of the sound is found to be 332 m/s. A large gap of (332–280) m/s = 53 m/s cannot be judged by stating it as an experimental error. This seems that there is something wrong in this analysis.
Laplace’s correction
Laplace had pointed out that Newton’s assumption was wrong. According to Laplace, the changes in pressure and volume of a gas, when sound waves are propagated through it, are not isothermal but are adiabatic.
Hence unser adiabatic condition
P{{\mathbf{V}}^{\gamma }}=constant
Differentiating we get, P\cdot \gamma {{\mathbf{V}}^{{\gamma -1}}}(d\mathbf{V})+{{\mathbf{V}}^{\gamma }}dP=0.
\gamma P=-\frac{{dP}}{{(d\mathbf{V/V})}} but B=-\frac{{dP}}{{d\mathbf{V/V}}}
B=\gamma P
Velocity of sound =\sqrt{{\frac{{\gamma p}}{\rho }}}
If sound wave is passing through air at NTP then V=\sqrt{{\frac{{\gamma P}}{\rho }}}=\sqrt{{\frac{{1.41\times 1.013\times {{{10}}^{5}}}}{{1.29}}}}=332.7\,\mathbf{m/s} \gamma =1.41\,for air
This agrees fairly well with the experimental data.
Factors effecting velocity of sound
1.
Effect of density: The velocity of sound in a gaseous medium is V=\sqrt{{\frac{{\gamma P}}{\rho }}}. Clearly V\,\,\,\propto \,\,\,\frac{1}{{\sqrt{\rho }}}.
Therefore velocity of sound in hydrogen is 4 times the velocity of sound in oxygen.
2.
Effect of pressure: According to V=\sqrt{{\frac{{\gamma P}}{\rho }}} and as per standard gas equation, PV=nRT ( where n=m/M i.e mass/molar mass)
PV=\frac{{mRT}}{M}
\displaystyle \Rightarrow P\frac{V}{m}=\frac{{RT}}{M}
\displaystyle \Rightarrow \frac{P}{\rho }=\frac{{RT}}{M} ( \displaystyle \because \frac{1}{\rho }=\frac{V}{m}, r is the density) From above equation it is clear that for a given gas at a given temperature the quantity \displaystyle \frac{P}{\rho } is a constant . Hence if pressure is increased the density will also increase by same factor hence the velocity of sound remains constant. At constant temperature, velocity of sound is independent of pressure ( v\,\propto \,\,P{}^\circ ).
3.
Effect of temperature: From the above discussion it is very clear that \displaystyle \frac{P}{\rho }=\frac{{RT}}{M}
therefore V=\sqrt{{\frac{{\gamma P}}{\rho }}}=\sqrt{{\frac{{\gamma RT}}{M}}}
hence v\,\propto \,\,\sqrt{T}. Therefore sound would travel faster on a hot day than on a cold day.
Important For small temperatures the velocity of sound varies linearly with temperature.
See detailed explanation in the video lecture
at a temperature t oC the velocity of sound is given as {{V}_{t}}={{V}_{{_{0}}}}+0.61\times t\,\,\,m/s where Vo is the velocity of sound at 0 oC.
Hence velocity of sound in air increases approximately by 0.61 m/s for every degree rise in temperature .
4.
Effect of humidity: The pressure of water vapours in air changes its density. That is why the velocity of sound changes with humidity of air.
Suppose
{{\rho }_{m}}= density of moist air, {{\rho }_{d}}= density of dry air , {{V}_{m}}= velocity of sound in moist air
{{V}_{d}}=velocity of sound in dry air
{{V}_{m}}=\sqrt{{\frac{{\gamma P}}{{{{\rho }_{m}}}}}} and {{V}_{d}}=\sqrt{{\frac{{\gamma P}}{{{{\rho }_{d}}}}}},\,\,\,\,\,\,\,\frac{{{{V}_{m}}}}{{{{V}_{d}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\sqrt{{\frac{{{{\rho }_{d}}}}{{{{\rho }_{m}}}}}}
The presence of water vapour reduces the density of air
{{\rho }_{m}}<{{\rho }_{d}}
{{V}_{m}}>{{V}_{d}}
Illustration
Find the temperature at which the velocity of sound in air will be twice the velocity of sound in air at 0°C.
Solution:
We know that
\frac{{{{v}_{1}}}}{{{{v}_{0}}}}\,=\,\sqrt{{\frac{{{{T}_{1}}}}{{{{T}_{0}}}}}}
Here, v1 = 2v0, and T0 = 273 K. Hence 2 = \sqrt{{\frac{T}{{273}}}}
or T = 4 ×273 = 1092 K
or t = 1092 – 273 = 819 °C
Illustration
Determine the speed of sound waves in water, and find the wavelength of a wave having a frequency of 242 Hz. Take Bwater = 2 × 109 Pa.
Solution:
Speed of sound wave, v = \sqrt{{\frac{B}{\rho }}} = \sqrt{{\frac{{(2\,\times \,{{{10}}^{9}})}}{{{{{10}}^{3}}}}}} = 1414 m/s
Wavelength, l = \frac{v}{f} = 5.84
Intensity of the Wave
The amount of energy flows perpendicular by from a plane per unit area per unit time. This is also known as “current energy”
Intensity\,\,of\,\,wave=\frac{{Total\,\,energy}}{{SurfaceArea\,\,of\,\,layer\times Time\,\,taken\,\,to\,\,cross\,\,the\,\,layer}}
\displaystyle I=\frac{1}{2}\rho {{\omega }^{2}}{{a}^{2}}V=2{{\pi }^{2}}\rho {{\nu }^{2}}{{a}^{2}}V
Let a source S having power P emits waves in all direction in a non-absorbing medium
and if the intensity of wave at a distance of r from source be I, then
I = Power /Surface area
\displaystyle \begin{array}{l}I=\frac{P}{{4\pi {{r}^{2}}}}\\\Rightarrow I\propto \frac{1}{{{{r}^{2}}}}\left( {Inverse\,\,square\,\,law} \right)\end{array}
Musical Sound, Noise & Loudness
A series of sound pulses following one another in a regular fashion with no sudden change in amplitude gives pleasant effect on our mind and is called music. On the contrary, the irregular sound pulses having sudden variation in amplitude gives unpleasant effect on mind and such a sound is called noise.
Interval : The ratio of the frequencies of the two notes is called the interval between them e.g. interval between two notes of frequencies 256 Hz and 512 Hz is 1 : 2.
|
Name of interval |
Frequency ratio |
|
Unison |
1 : 1 |
|
Octave |
2 : 1 |
|
Major tone |
9 : 8 |
|
Minor tone |
10 : 9 |
|
Semi tone |
16 : 15 |
LOUDNESS
Human ear is sensitive for an extremely large range of intensities. So, a logarithmic, rather than an arithmetic, scale is convenient. Accordingly, loudness b of a sound wave having intensity I is defined by the following equation.
Loudness b = 10 log10 \displaystyle \left( {\frac{I}{{{{I}_{o}}}}} \right) decibel
where Io = 10–12 W/m2 is the reference intensity (threshold level for normal human ear) level to which any intensity I is compared.The upper limit of intensity of sound which can be tolerated by human ear is 1 W/m2. This is called threshold of pain.
The loudness is measured in bel (B) but for practical purpose bel is pretty large, a smaller unit decibel in defined which is equal to 0.1 bel. It is denoted by dB.
In the formula of Loudness b = 10 log10 \displaystyle \left( {\frac{I}{{{{I}_{o}}}}} \right), If we put I=10-12(threshold level for normal human ear) we get b = 0 decibel where if we put I= 1 (threshold of pain) we get b = 120 decibel, hence for a human ear the safe audible range is from 0 to 120 decibel. Sound above 120 decibel produce bad effects on human being.
Illustration
The power of sound from the speaker of a radio is 20 mW. By turning the knob of volume control the power of sound is increased to 400 mW. The power increase in dB as compared to the original power is (log10 2 = 0.3)
(a) 1.3 dB
(b) 3.1 dB
(c) 13 dB
(d) 30.1 dB
Sol.:
As P\propto I,
S{{L}_{2}}-S{{L}_{1}}=10\log \left( {\frac{{{{I}_{2}}}}{{{{I}_{1}}}}} \right)=10\log \left( {\frac{{{{P}_{2}}}}{{{{P}_{1}}}}} \right)
=10\log \left( {\frac{{400}}{{20}}} \right)=10\log 20=13\,\,\text{dB}
∴ (c)
Acoustic
It is a branch of physics, which deal with the designs of building to produce pleasant sound system in building and is called acoustic. Due to absorption of sound, it die out after the source has been switched off. This phenomenon is called reverberation and the time for which intensity of sound fall to one millionth of the maximum steady value is called reverberation time.
Sabine law : Sabine derived an expression of the reverberation time which is t=K.\frac{V}{{\alpha S}}; where K is constant, V = Volume of the hall, S = Surface area exposed to the sound a =Co-efficient of absorption.
An Acoustically good hall has following qualities:
1.
Sound heard sufficiently loud
2.
No undue echo of sound
3.
No overlapping of successive sound
4.
Quality of original sound is maintained
5.
No extraneous sound
6.
Intensity distributed uniformly in different parts of the Hall.
To achieve the above qualities the reverberation time should be controlled that may be done as follows
By hanging heavy curtains on the doors.
By having few open windows in the hall.
By having large audience.
By using absorbing materials in the walls and roofs of the hall.
Characteristics of sound
(i)
Intensity or Loudness: It is purely subjective and hence cannot be measured with instrument. The term loudness describes the human perception of sound. A sound wave of higher intensity is perceived as louder than a wave of lower intensity. However, the relation is not linear. The sensation of loudness is roughly proportional to the logarithm of intensity.
Lµ log I
The loudness of sound depends upon the amplitude of sounding body and the area of sounding body. It is measured in dB (decibel).
(ii)
Frequency or Pitch: The term pitch refers to the attribute of a sound sensation that distinguishes a ‘high’ note from a ‘low’ note. Like loudness, the pitch is also subjective. It is related to the objected quantity frequency, higher the frequency, higher is the pitch.
(iii)
Quality or Timbre: A musical instrument vibrates with many frequencies at the same time–a lowest frequency, called the fundamental, and its multiples, called overtones. The quality (or timbre) of any musical sound is determined by the number of overtones and their relative intensities. The sounds of different instruments in a musical concert are said to differ in quality, though they may have same fundamental frequency.
Echo and Reverberation
For human beings, the persistence of hearing 1/10 of a sound. The effect of a sharp sound once heard remains in the mind for next 0.1 s.
Echo is the return of the sound of a syllable after the original sound is dead.
Reverberation is the persistence of the sound of a syllable for some time till it falls below the minimum level of audibility (about 10-12 W/m2). The time taken by the sound intensity to fall by a factor of 10–6 is called reverberation time. For big domelike structures such as Taj Mahal at Agra, the reverberation time may be as large as 20-30 seconds.
Objective Assignment
Q.1
A travelling wave in a stretched string is described by the equation, y = A sin(kx – wt). The maximum particle velocity is
(a) Aw
(b) w/k
(c) \frac{{d\omega }}{{dk}}
(d) \frac{x}{t}
Ans. (a)
Q.2
As a wave propagates (choose incorrect one)
(a) the wave intensity remains constant for a plane wave
(b) the wave intensity decreases as the inverse of the distance from source for a spherical wave
(c) the wave intensity falls as the inverse square of the distance from a spherical wave
(d) total intensity of the spherical wave over the spherical surface centred at the source remains constant al all time
Ans. (b)
Q.3
Which of the following properties of sound is not affected by change in the temperature of air?
(a) wavelength
(b) intensity
(c) amplitude
(d) frequency
Ans. (d)
Q.4
Sound waves in air differ from the electromagnetic waves in that they cannot be
(a) diffracted
(b) polarized
(c) reflected
(d) refracted
Ans. (b)
Q.5
Velocity of sound in a gas is proportional to
(a) square root of isothermal elasticity
(b) isothermal elasticity
(c) square root of adiabatic elasticity
(d) adiabatic elasticity
Ans. (c)
Q.6
When you speak to your friend, which of the following quantities have a unique value in the sound produced?
(a) amplitude
(b) wave velocity
(c) frequency
(d) wavelength
Ans. (b)
Q.7
If wavelength changes by \Delta \lambda then change in propagation vector is
(a) \Delta k
(b) 2\pi \Delta \lambda
(c) \frac{{2\pi }}{\lambda }\Delta \lambda
(d) \frac{{2\pi }}{{{{\lambda }^{2}}}}\Delta \lambda
Ans. (d)
Q.8
The ratio of the velocity of body and velocity of sound is known as
(a) laplace number
(b) positive integer
(c) stable number
(d) mach number
Ans. (d)
Q.9
The property of a medium necessary for wave propagation is its
(a) elasticity
(b) low resistance
(c) inertia
(d) all of above
Ans. (d)
Q.10
At what temperature the speed of sound in air will be 1.5 times its value at 27°C in air?
(a) 102°C
(b) 204°C
(c) 240°
(d) 402°C
Ans. (d)
Q.11
Under similar conditions of temperature and pressure, the velocity of sound is maximum?
(a) \mathbf{C}{{\mathbf{O}}_{\mathbf{2}}}
(b) {{\mathbf{H}}_{\mathbf{2}}}
(c) {{\mathbf{N}}_{\mathbf{2}}}
(d) {{\mathbf{O}}_{\mathbf{2}}}
Ans. (b)
Q.12
A tuning fork produces a wave of wavelength 110 cm in air at 0°C. Its wavelength in air at 25°C would be
(a) 110 cm
(b) 115 cm
(c) 160 cm
(d) 125 cm
Ans. (b)
Q.13
The mass of a 4m long string is 0.01 kg. It is stretch by a force of 400 N. The velocity of the transverse wave propagating in the string is
(a) \mathbf{100}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{1}}}}
(b) 2\mathbf{00}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{1}}}}
(c) 3\mathbf{00}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{1}}}}
(d) 4\mathbf{00}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{1}}}}
Ans. (d)
Q.14
A transverse wave is given by y=a\sin 2\pi (ft-x/\lambda ). The maximum particle velocity is four times the wave velocity, when
(a) \lambda =2\pi a
(b) \lambda =\pi a
(c) \lambda =\pi a/4
(d) \lambda =\pi a/2
Ans. (d)
Q.15
The wavelength of a wave in a medium is 0.5 m. Due to this wave the phase difference between two particles of the medium is \pi /5. The minimum distance between these points is
(a) 5 km
(b) 5m
(c) 5 mm
(d) 5 cm
Ans. (d)
Q.16
The frequency of a tuning fork is 384 Hz and velocity of sound in air is \mathbf{352}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{1}}}}. How far sound has traveled when fork completes 36 vibrations
(a) 33 m
(b) 16.5 m
(c) 11 m
(d) 22 m
Ans. (a)
Q.17
The velocity of sound is {{V}_{s}} in air. If density of air is increased twice then the new velocity of sound will be
(a) {{V}_{s}}
(b) \frac{{{{V}_{s}}}}{{\sqrt{2}}}
(c) \sqrt{2}{{V}_{s}}
(d) \frac{3}{2}{{V}_{s}}
Ans. (c)
Q.18
The relation between the objective measurement of intensity of sound, I and the subjective sensory response called loudness L is given by
(a) L=K\log {{I}^{2}}
(b) I=K\log L
(c) L=I
(d) L=K\log \,I
Ans. (d)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
