Video Lecture
Theory For Making Notes
Derivation of expression for period of a Simple Pendulum
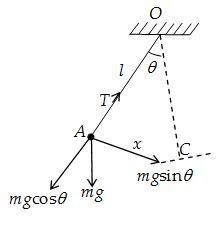
The particle in a simple pendulum moves in an arc of a circle of radius l = OA (See figure). The forces acting on the particle are its weight mg and the tension T along the string. The tangential component of the resultant force, from the figure, is
FT = – mg sin θ …(i)
where the minus sign appears because its direction is opposite to the displacement x = CA. The equation for the tangential motion is
Since the particle moves along a circle of radius l, we may use Equations, aT= \displaystyle {{a}_{T}}=R\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}, with R replaced by l, to express the tangential acceleration. That is,
\displaystyle {{a}_{T}}=l\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}
Thus, the equation for the tangential motion, from equation (i) is
\displaystyle ml\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}=-mg\sin \theta
or \displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}+\frac{g}{l}\sin \theta =0 ….(ii)
This equation is not in the standard form because of the presence of sin θ instead of just θ. However, if the angle θ is small, which is true in case the amplitude of the oscillations is very small, we may use the series expansion of sin θ \displaystyle \left( {\sin \theta =\theta -\frac{{{{\theta }^{3}}}}{{3!}}+……} \right) and keep only the first term. So we write \displaystyle \sin \theta \simeq \theta in equation for the motion of the pendulum, which becomes
\displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}+\frac{g}{l}\theta =0
This equation is identical to standard equation, \displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}+{{\omega }^{2}}\theta =0. Thus we may conclude that, within our approximation, the angular motion of the pendulum is simple harmonic, with
\displaystyle {{\omega }^{2}}=\frac{g}{l}
The angle θ can thus be expressed in the form
\displaystyle \theta ={{\theta }_{0}}\sin \ (\omega t\pm \phi ) where \displaystyle {{\theta }_{0}}is called angular amplitude.
Using Equation, T = 2p/w, we can express the period of oscillation of the pendulum as
\displaystyle T=2\pi \sqrt{{\frac{l}{g}}}
For large amplitudes the approximation \displaystyle \sin \theta \simeq \theta is not valid and the calculation of the period is more complex.
It is relatively easy and instructive to obtain a better approximation for T. Again using the series expansion of sin q, keeping only the first two terms, we may write
\displaystyle \sin \theta =\theta -\frac{{{{\theta }^{3}}}}{{3!}}+….\approx \theta \left( {1-\frac{{{{\theta }^{2}}}}{6}} \right)
which when inserted in equation (ii) gives a second-order approximation to the equation of motion,
\displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}+\frac{g}{l}\left( {1-\frac{{{{\theta }^{2}}}}{6}} \right)\theta =0
We may make another approximation by replacing q2 in the parentheses by \displaystyle {{({{\theta }^{2}})}_{{av}}}=\tfrac{1}{2}\theta _{0}^{2}. Then
\displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}+\frac{g}{l}\left( {1-\frac{{\theta _{0}^{2}}}{{12}}} \right)\theta =0
which again is an equation of type \displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}\,+\,{{\omega }^{2}}\theta =0. Therefore, up to this order of approximation
\displaystyle {{\omega }^{2}}=\frac{g}{l}\left( {1-\frac{{\theta _{0}^{2}}}{{12}}} \right)
Then \displaystyle T’=\frac{{2\pi }}{\omega }=2\pi \sqrt{{\frac{l}{g}}}{{\left( {1-\frac{{\theta _{0}^{2}}}{{12}}} \right)}^{{-1/2}}}
\displaystyle \approx \ 2\pi \sqrt{{\frac{l}{g}}}\ \left( {1+\frac{{\theta _{0}^{2}}}{{24}}} \right)
A more precise approximation gives
\displaystyle T=2\pi \sqrt{{\frac{l}{g}}}\left( {1+\frac{{\theta _{0}^{2}}}{{16}}+….} \right)
where the amplitude q0 must be expressed in radians. This is a sufficient approximation for most practical situations. In fact, the corrective term \displaystyle \theta _{0}^{2}/16 amounts to less than 1% for amplitudes less than 23° or 0.40 radians.
Important Points about Pendulum :
1.
The time period is independent of the mass of the bob. Therefore, if the solid bob is replaced by a hollow sphere of the same radius but different mass, the time period remains the same. Similarly, if a girl is swinging in a swing and another girl sits with her then there is no change in time period.
2.
The time period of a simple pendulum is independent of the amplitude of motion provided the motion is simple harmonic.
3.
The graph between T and l will be a parabola while the graph between \displaystyle {{T}^{2}}and l will be a straight line.
4.
If the length of simple pendulum is comparable to the radius of the earth (Re), then
\displaystyle T=2\pi \sqrt{{\left[ {\frac{{{{R}_{e}}}}{{g(1+{{R}_{e}}/l)}}} \right]}}
We consider the following two cases :
(i) When ,l = Re, then
\displaystyle T=2\pi \sqrt{{\left( {\frac{{\operatorname{Re}}}{{2g}}} \right)}}=2\pi \sqrt{{\left[ {\frac{{(6.4\times {{{10}}^{6}})}}{{2\times 9.8}}} \right]}}= 60 min
(ii) When \displaystyle l\to \infty \ i.e.,\ l>>{{R}_{e}}, then
\displaystyle T=2\pi \sqrt{{\left( {\frac{{{{R}_{e}}}}{g}} \right)}}=2\pi \sqrt{{\left[ {\frac{{(6.4\times {{{10}}^{6}})}}{{9.8}}} \right]}}= 84.63 min.
5.
If the thread of the simple pendulum is replaced by a wire then due to change in temperature its length will increase. Therefore, the time period will increase.
Now, \displaystyle l={{l}_{0}}(1+\alpha \Delta \theta )
Where Δθ is the change in temperature and a is the coefficient of linear expansion of the wire.
\displaystyle T=2\pi \sqrt{{\left( {\frac{1}{g}} \right)}}\ \ \ \text{and}\ \ {{T}_{0}}=2\pi \sqrt{{\left( {\frac{{{{l}_{0}}}}{g}} \right)}}
\displaystyle \frac{T}{{{{T}_{0}}}}=\sqrt{{\left( {\frac{l}{{{{l}_{0}}}}} \right)}}={{(1+\alpha \Delta \theta )}^{{1/2}}}=\left( {1+\frac{1}{2}\propto \Delta \theta } \right)
\displaystyle \frac{T}{{{{T}_{0}}}}-1=\frac{1}{2}\alpha \Delta \theta \ \ \text{or}\ \ \frac{{\Delta T}}{{{{T}_{0}}}}=\frac{1}{2}\alpha \Delta \theta
6.
If bob of a simple pendulum is made to oscillate in a fluid of density r0 (r0<r) where r is the density of the material of the bob, then the time period of simple pendulum will increase.
In this case, \displaystyle {g}’=g\left( {1-\frac{{{{\rho }_{0}}}}{\rho }} \right)because \displaystyle m{g}’=mg-\text{thrust}
\displaystyle \therefore \ \ \ \frac{{{T}’}}{T}=\sqrt{{\left( {\frac{g}{{{g}’}}} \right)}}=\sqrt{{\left[ {\frac{1}{{(1-{{\rho }_{0}}/\rho )}}} \right]}}=\sqrt{{\left( {\frac{\rho }{{\rho -{{\rho }_{0}}}}} \right)}}
Period of oscillation of a vertical spring-mass system
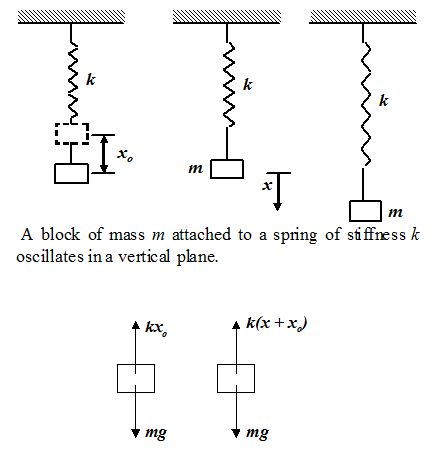
Let xobe the deformation in the spring in equilibrium.
Then kxo= mg
When the block is further displaced by x, the net restoring force is given by
F = -[k(x + xo) – mg]
or F = –kx(because kxo= mg)
Using second law of motion,
m\frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}=-kx
or \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}+\left( {\frac{k}{m}} \right)x=0
Thus, w2 = \frac{k}{m} or T = 2π \sqrt{{\frac{m}{k}}}
Note that gravity does not influence the time period of the spring-mass system, it merely changes the equilibrium position.
Alternate method:
Total energy of the system at any instant is given by
\displaystyle E=\frac{1}{2}m{{V}^{2}}+\frac{1}{2}K{{x}^{2}}
on differentiating the equation with respect to time we get
\displaystyle \frac{{dE}}{{dt}}=\frac{1}{2}m2V\frac{{dV}}{{dt}}+\frac{1}{2}K.2x\frac{{dx}}{{dt}}=0
\displaystyle \frac{{dV}}{{dt}}=-\frac{K}{m}x
\displaystyle \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}+\frac{K}{m}x=0
Compare it with standard equation of simple harmonic motion
\displaystyle \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}+{{\omega }^{2}}x=0
\displaystyle \omega =\sqrt{{\frac{K}{m}}}
or \displaystyle T=2\pi \sqrt{{\frac{m}{K}}}
Series and Parallel Combinations of Springs
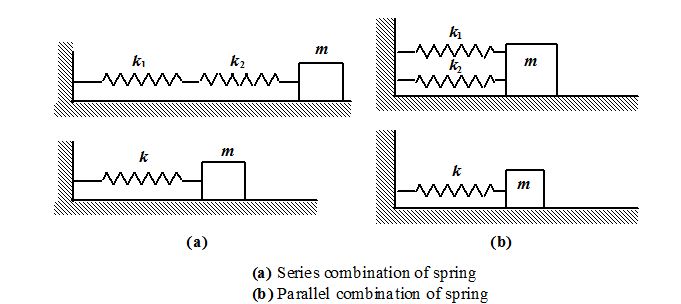
When two springs are joined in series, the equivalent stiffness of the combination is given by :
\frac{1}{k}=\frac{1}{{{{k}_{1}}}}+\frac{1}{{{{k}_{2}}}}
When two springs are joined in parallel, the equivalent stiffness of the combination is given by
k = k1 + k2
Illustration
If length of second pendulum is increased by 21%. Then how many oscillations decrease per day?
Solution
No. of oscillation made by second pendulum per day.
\displaystyle {{N}_{1}}=\frac{{24\times 60\times 60}}{2}
When length is increased by 21% then time period
\displaystyle \frac{{{{T}_{2}}}}{{{{T}_{1}}}}=\sqrt{{\frac{{1.21L}}{L}}}
\displaystyle {{T}_{2}}=2.2\sec
No of oscillation per day.
\displaystyle {{N}_{2}}=\frac{{24\times 60\times 60}}{{2.2}}
Difference of oscillation \displaystyle ={{N}_{1}}-{{N}_{2}}
\displaystyle =\frac{{24\times 60\times 60}}{2}-\frac{{24\times 60\times 60}}{{2.2}}
= 3927
Illustration
A 2 kg block is attached to a spring for which k = 200 N/m. It is held at an extension of 5 cm and then released at t = 0. Find
(a) the displacement as a function of time
(b) the velocity when x = +A/2;
(c) the acceleration when x = +A/2, where A is the amplitude.
Solution
(a) We need to find a, w, and f in equation. The amplitude is the maximum extension; that is,
A = 0.05 m
We know the angular frequency of the spring-mass system is given by
w = \sqrt{{\frac{k}{m}}}=10\,\,rad/s
To find f we note that at t = 0 we are given x = +A and v = 0.
Thus, from the equation of displacement and velocity, we get
x = A sin (w t + Φ)
A = A sin (0 + Φ)
v = w A cos (w t + Φ)
0 = 10 A cos (0 + Φ)
Since sin Φ = 1 and cos Φ = 0, it follows that fΦ= π/2 rad. Thus,
x = 0.05 sin \left( {10t+\frac{\pi }{2}} \right)\,m ……..(i)
(b) In order to find the velocity we have to find phase when x = A/2. Equation (i) yields
\frac{1}{2}=\sin \left( {10t+\frac{\pi }{2}} \right),
from which we get that (10 t + \frac{\pi }{2}) = \frac{\pi }{6} or \frac{{5\pi }}{6}
The velocity is given by
v = \frac{{dx}}{{dt}} = 0.5 cos \left( {10t+\frac{\pi }{2}} \right)
= 0.5 cos \frac{\pi }{6} or 0.5 cos \frac{{5\pi }}{6}
= +0.43 m/s or -0.43 m/s
At a given position, there are two velocities of equal magnitude but of opposite directions.
(c) The acceleration at x = A/2 may be found from the equation,
a = -\frac{k}{m}x=-{{\omega }^{2}}x = -(10 rad/s)2(0.05/2 m) = -2.5 m/s2
Practice Questions (Level-1)
Q.1
A simple pendulum of frequency n is taken up to a certain height above the ground and then dropped along with its support so that it falls freely under gravity. The frequency of oscillations of the falling pendulum will
(a) remain equal to n
(b) become greater than n
(c) become less than n
(c) become zero
Ans. (d)
Q.2
A pendulum is suspended in a lift and its period of oscillation, when lift is stationary is T0 With what acceleration a must the lift be raised for the period of oscillation of the pendulum to be T0/2
(a) -3g (b) 4g (c) 6g (d) -4g
Ans. (a)
Q.3
A uniform spring has a certain mass suspended from it and its period for vertical oscillations is T1. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillations now is T2. The ratio T2/T1 is
(a) \displaystyle \frac{1}{2}
(b) \displaystyle \frac{1}{{\sqrt{2}}}
(c) 2
(d) \displaystyle \sqrt{2}
Ans. (b)
Q.4
A spring of force constant k is cut into two equal halves. The force constant of each half is
(a) \displaystyle \frac{k}{{\sqrt{2}}}
(b) \displaystyle \frac{k}{2}
(c) k
(d) 2k
Ans. (d)
Q.5
A hollow sphere is filled with water. It is hung by a long thread. As the water flows out of a hole at the bottom, the period of oscillation will:
(a) First increase and then decrease
(b) First decrease and then increase
(c) Go on increasing
(d) Go on decreasing
Ans. (a)
Q.6
The time period of a simple pendulum inside a stationary lift is x=-\frac{1}{2},y=\frac{1}{2}s. What will be the time period when the lift moves upwards with an acceleration \eta =\frac{{p({{r}^{2}}-{{x}^{2}})}}{{4vl}}?
(a) \eta
(b) v=at+\frac{b}{{t+c}}
(c) \displaystyle \overset{\to }{\mathop{A}}\,,\overset{\to }{\mathop{B}}\,\,\,\,and\,\,\,\,\overset{\to }{\mathop{C}}\,
(d) \overset{\to }{\mathop{A}}\,+\overset{\to }{\mathop{B}}\,=\overset{\to }{\mathop{C}}\,
Ans. (c)
Q.7
If the metal bob of a simple pendulum is replaced by a wooden bob, then its time period will
(a) increase
(b) decrease
(c) remain the same
(d) may increase or decrease
Ans. (c)
Q.8
In figures a and b, combinations of two springs of force constants k1 and k2 (where k1 = k2) are given. Then the ratio of their time periods is
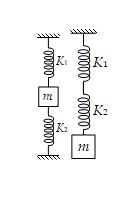
(a) 2 : 1
(b) 1 : 2
(c) 1 : 1
(d) None
Ans. (b)
Q.9
Four massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in Fig.). If the mass M is displaced in the horizontal direction, then the frequency of the system:
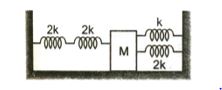
(a) \displaystyle \frac{{3K}}{4}
(b) \displaystyle {{y}_{2}}=3\sin \left( {\omega t+\frac{\pi }{3}} \right)
(c) \displaystyle \frac{{2\pi }}{\lambda }\left( {{{L}_{2}}-{{L}_{1}}} \right)
(d) \displaystyle \frac{{2\pi }}{\lambda }\left( {{{n}_{1}}{{L}_{1}}-{{n}_{2}}{{L}_{2}}} \right)
Ans. (b)
Q.10
A mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relation is
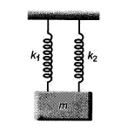
(a) \displaystyle {{T}^{2}}\,=\,T_{1}^{2}\,+\,T_{2}^{2}
(b) \displaystyle {{T}^{{-2}}}\,=\,T_{1}^{{-2}}\,+\,T_{2}^{{-2}}
(c) \displaystyle {{T}^{{-1}}}\,=\,T_{1}^{{-1}}\,+\,T_{2}^{{-1}}
(d) \displaystyle T={{T}_{1}}+{{T}_{2}}
Ans. (b)
Q.11
If both spring constants K1 and K2 are increased to 4K1 and 4K2 respectively, what will be the new frequency, if f was the original frequency:
(a) f (b) 2 f (c) ½ f (d) 4 f
Ans. (b)
Practice Questions (Level-2)
Q.1
A person measures the time period of a simple pendulum inside a stationary lift and finds it to be T. If the lift starts accelerating upwards with an acceleration of g/3, the time period of the pendulum will be
(a) \displaystyle \sqrt{3}\ T
(b) \displaystyle \frac{{\sqrt{3}T}}{2}
(c) \displaystyle \frac{T}{{\sqrt{3}}}
(d) \displaystyle \frac{T}{3}
Ans. (b)
Q.2
A simple pendulum with a brass bob has a time period T. The bob is now immersed in a non-viscous liquid and oscillated. If the density of the liquid is 1/8 that of brass, the time period of the same pendulum will be
(a) \displaystyle \sqrt{{\frac{8}{7}}}\ T
(b) \displaystyle \frac{8}{7}\ T
(c) \displaystyle \frac{{{{8}^{2}}}}{{{{7}^{2}}}}T
(d) T
Ans. (a)
Q.3
A simple pendulum of frequency f has a metal bob. If the bob is charged negatively and is allowed to oscillate with a positively charged plate placed under it, the frequency will
(a) remain equal to f
(b) become less than f
(c) become more than f
(d) become zero
Ans. (c)
Q.4
A bob of mass M is attached to the lower end of a vertical string of length L an cross-sectional area A. The Young’s modulus of the material of the string is Y. If the bob executes SHM in the vertical direction, find the frequency of these oscillations.
(a) \displaystyle v=\frac{1}{\pi }\sqrt{{\left( {\frac{{YA}}{{ML}}} \right)}}
(b) \displaystyle v=\frac{1}{{2\pi }}\sqrt{{\left( {\frac{{YA}}{{ML}}} \right)}}
(c) \displaystyle v=\frac{1}{{4\pi }}\sqrt{{\left( {\frac{{YA}}{{ML}}} \right)}}
(d) None
Ans. (b)
Q.5
A solid brass sphere is hung from a spring whose mass is negligible compared to that of the sphere. The sphere is set into vertical oscillations and its time period if found to be T. The sphere is now completely immersed in a liquid whose density is 1/8th that of brass. The time period of vertical oscillations with the sphere always remaining immersed in the liquid will be equal to
(a) T
(b) \displaystyle \sqrt{{\frac{7}{8}}}\ T
(c) \displaystyle \frac{7}{8}T
(d) \displaystyle {{\left( {\frac{7}{8}} \right)}^{2}}T
Ans. (a)
Q.6
A simple pendulum is made by attaching a 1 kg bob to a 5 m copper wire of diameter 0.08 cm and it has a certain period of oscillation. Next a 10 kg bob is substituted for 1 kg bob. Calculate the change in the period, if any. Young’s modulus of copper = 12.4 × 1010 Nm–2.
(a) 0.03s (b) 0.01sec (c) 0.003 s (d) None
Ans. (c)
Q.7
A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4 \displaystyle m/{{s}^{2}}. Its period of oscillation is
(a) 1.90 s (b) 1.70 s (c) 2.30 s (d) 1.40 s
Ans. (a)
Q.8
Two springs of equal lengths and equal cross-sectional areas are made of materials whose Young’s modulii are in the ratio of 3 : 2. They are suspended and loaded with the same mass. When stretched and released, they will oscillate with time periods in the ratio of
(a) \displaystyle \sqrt{2}\ :\ \sqrt{2}
(b) 3 : 2
(c) \displaystyle 3\sqrt{3}\ :\ 2\sqrt{2}
(d) \displaystyle 9:4
Ans. (a)
Q.9
Two bodies A and B of equal masses are suspended from two separate springs of force constants k1 and k2 respectively. If the two bodies oscillate such that their maximum velocities are equal, the ratio of the amplitudes of oscillation of A and B will be
(a) \displaystyle \frac{{{{k}_{1}}}}{{{{k}_{2}}}}
(b) \displaystyle \sqrt{{\frac{{{{k}_{1}}}}{{{{k}_{2}}}}}}
(c) \displaystyle \frac{{{{k}_{2}}}}{{{{k}_{1}}}}
(d) \displaystyle \sqrt{{\frac{{{{k}_{2}}}}{{{{k}_{1}}}}}}
Ans. (d)
Q.10
A spring has a natural length of 50 cm and a force constant of 2.0 × 103 Nm–1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down further stretching the spring to a length of 58 cm and released, it executes simple harmonic motion. What is the net force on the body when it is at its lowermost position of its oscillation? Take g = 10 ms–2.
(a) 20 N (b) 40 N (c) 60 N (d) 80 N
Ans. (c)
Q.11
A man is standing on a weighing machine placed on a horizontal platform that is executing vertical simple harmonic motion of angular frequency \displaystyle 2\sqrt{2} rad s–1. The maximum and minimum readings of the machine are 65 kg and 55 kg. Find the true mass of the man.
(a) 40 kg (b) 20 kg (c) 10 kg (d) 60 kg
Ans. (d)
Q.12
A simple pendulum with a solid metal bob has a period T. The metal bob is now immersed in a liquid of density one-tenth that of the bob. The liquid is non-viscous. Now that period of the same pendulum with its bob remaining all the time in the liquid will be:
(a) T
(b) \displaystyle \frac{{2\lambda }}{{\mu -1}}
(c) \displaystyle \lambda =\frac{D}{{{{d}^{2}}}}
(d) \displaystyle {{I}_{1}}={{I}_{2}}
Ans. (c)
Q.13
Two simple pendulums of length 1 m and 16 m respectively are both given small displacements in the same direction at the same instant. They will again be in phase after the shorter pendulum has completed n oscillations where n is
(a) 1/4 (b) 4/3 (c) 5 (d) 4
Ans. (b)
Q.14
A mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1 and k2. The time period of the suspended mass will be
(a) \displaystyle \frac{{2\pi }}{\lambda }\left( {{{n}_{2}}{{L}_{1}}-{{n}_{1}}{{L}_{2}}} \right)
(b) \displaystyle \frac{{2\pi }}{\lambda }\left( {\frac{{{{L}_{1}}}}{{{{n}_{1}}}}-\frac{{{{L}_{1}}}}{{{{n}_{2}}}}} \right)
(c) \displaystyle \frac{I}{2}
(d) \displaystyle \frac{I}{4}
Ans. (d)
Q.15
A mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200 N/m, the upper end of which is fixed to a rigid support. Which of the following statement is true?
(a) In equilibrium, the spring will be stretched by 1 cm
(b) If the mass is raised till the spring becomes unstretched and then released, it will go down by 2 cm before moving upwards
(c) The frequency of oscillation will be nearly 5 Hz
(d) All of the above.
Ans. (d)
Q.16
Two bodies M and N of equal masses are suspended from two separate massless springs of spring constants k1 and k2 If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of M to the on N is
(a) \displaystyle \frac{{4\hat{i}}}{{\sqrt{{18}}}}\frac{{\hat{j}}}{{\sqrt{{18}}}}\frac{k}{{\sqrt{{18}}}}
(b) \displaystyle \frac{{4\hat{i}}}{{\sqrt{{18}}}}+\frac{{\hat{j}}}{{\sqrt{{18}}}}+\frac{k}{{\sqrt{{18}}}}
(c) \displaystyle 4\hat{i}+\hat{j}+k
(d) \displaystyle \left( {P+\frac{a}{{{{V}^{2}}}}} \right)\left( {Vb} \right)=RT,
Ans. (d)
Q.17
A particle is attached to a vertical spring and is pulled down a distance 0.04 m below its equilibrium position and is released from rest. The initial upward acceleration of the particle is 0.30 \overset{\to }{\mathop{A}}\,\,\,and\,\,\overset{\to }{\mathop{B}}\,. The period of the oscillation is
(a) 4.08 s (b) 1.92 s (c) 3.90 s (d) 2.29 s
Ans. (d)
Q.18
The period of oscillation of a simple pendulum of length l suspended from the roof of a vehicle, which moves without friction down an inclined plane of inclination \displaystyle \overset{\to }{\mathop{B}}\,=3\hat{i}+4\hat{j}-5\hat{k}, is given by
(a) \displaystyle {{10}^{6}}\text{erg/s}
(b) \displaystyle {{10}^{7}}\text{erg/s}
(c) \displaystyle {{10}^{9}}\text{erg/s}
(d) \displaystyle {{10}^{{11}}}\text{erg/s}
Ans. (a)
Q.19
A small bob attached to a light inextensible thread of length l has a periodic time T when allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end O of a vertical rigid rod of length 3l/4. If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be
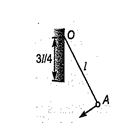
(a) 3T/4 (b) 4T/5 (c) 2T/3 (d) 5T/6
Ans. (a)
Q.20
All the surfaces shown in figure are frictionless. The mass of the car is M, that of the block is m and the spring has spring constant k. Initially, the car and the block are at rest and the string is stretched through a length x when the system is released. Find the amplitudes of SHM of the block and of car as seen from the road and the time period(s) of the two simple harmonic motions.
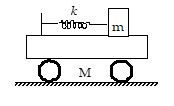
(a) \displaystyle \frac{{m{{x}_{0}}}}{{(M+m)}},\ \frac{{m{{x}_{0}}}}{{(M+m)}}, \displaystyle 2\pi \sqrt{{\left\{ {\frac{{mM}}{{k(M+m)}}} \right\}}}
(b) \displaystyle \frac{{m{{x}_{0}}}}{{(M+m)}},\ \frac{{m{{x}_{0}}}}{{(M+m)}}, \displaystyle \pi \sqrt{{\left\{ {\frac{{mM}}{{k(M+m)}}} \right\}}}
(c) \displaystyle \frac{{m{{x}_{0}}}}{{(M+m)}},\ \frac{{m{{x}_{0}}}}{{(M+m)}}, \displaystyle -2\pi \sqrt{{\left\{ {\frac{{mM}}{{k(M+m)}}} \right\}}}
(d) None
Ans. (a)
Q.21
One end of a light spring of force constant k is fixed to a block A of mass M placed on a horizontal frictionless table; the other end of the spring is fixed to a wall (figure). A smaller block B of mass m is placed on block A. The system is displaced by a small amount and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block? The coefficient of static friction between the two blocks is m.
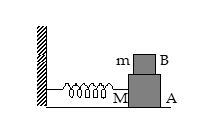
(a) \displaystyle \frac{{mk{{A}_{{\max }}}}}{{(M+m)}}=\mu mg\ \ \text{or}\ \ {{A}_{{\max }}}=\frac{{\mu (M+m)g}}{k}
(b) \displaystyle \frac{{mk{{A}_{{\max }}}}}{{(M+m)}}=\mu mg\ \ \text{or}\ \ {{A}_{{\max }}}=-\frac{{\mu (M+m)g}}{k}
(c) \displaystyle \frac{{mk{{A}_{{\max }}}}}{{(M+m)}}=-\mu mg\ \ \text{or}\ \ {{A}_{{\max }}}=\frac{{\mu (M-m)g}}{k}
(b) None
Ans. (a)
Q.22
A mass of 2 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in Figure. The mass of the spring and the pan is negligible.
When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion so that the mass gets detached from the pan? (Take g = 10 m/s2)

(a) 4.0 cm
(b) 8.0 cm
(c) 10.0 cm
(d) Any value less than 12.0 cm
Ans. (c)
Q.23
A mass of 0.5 kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m. The maximum compression of the spring would be

(a) 0.15 m (b) 0.12 m (c) 1.5 m (d) 0.5 m
Ans. (a)
Q.24
A block of mass 0.2 kg, which slides without friction on a 30° incline, is connected to the top of the incline by a massless spring of force constant 80 N/m as shown in figure. If the block is pulled slightly from its mean position, what is the period of oscillations?
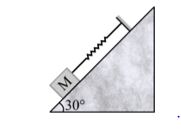
(a) p s
(b) \displaystyle \left| {\,\vec{P}\,} \right|=\left| {\,\vec{Q}\,} \right|,\,\,\left| {\,R\,} \right|=\sqrt{2}\,\left| {\,\vec{P}\,} \right|,
(c) \displaystyle \left| {\,\vec{P}+\vec{Q}\,} \right|+R=0.
(d) \displaystyle P\,\,and\,\,\vec{Q},\,\,\vec{Q}
Ans. (b)
Q.25
Molten-wax of mass m drops on a block of mass M, which is oscillating on a frictionless table as shown. Select the incorrect option:
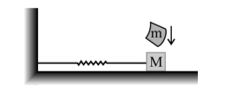
(a) If the collision takes place at extreme position, amplitude does not change
(b) If the collision takes place at mean position, amplitude decreases
(c) If the collision takes place at mean position, time period decreases
(d) If the collision takes place at extreme position, time period increases
Ans. (c)
