Video Lecture
Theory For Making Notes
Second Law of Thermodynamics
First law of thermodynamics merely explains the equivalence of work and heat. It does not explain why heat flows from bodies at higher temperatures to that at lower temperatures alsoit cannot explain why the efficiency of a heat engine is always less than unity. Whereas second law of thermodynamics provides answers to these questions.
Clausius statement :
Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time. In Simple words It is impossible for a self acting machine to transfer heat from a colder body to a hotter one without the aid of an external agency.
Kelvin’s statement :
It is impossible for a body or system to perform continuous work by cooling it to a temperature lower than the temperature of the coldest one of its surroundings.
Kelvin-Planck’s statement :
It is impossible to design an engine that extracts heat and fully utilises into work without producing any other effect In other words It is impossible to construct a heat engine which while working in a thermodynamic cycle exchange heat with one heat reservoir and produce a net positive work.
Heat Engine
Heat engine is a device which converts heat into work continuously through a cyclic process.
The essential parts of a heat engine are
(1) Source : It is a reservoir of heat at high temperature and infinite thermal capacity. Any amount of heat can be extracted from it.
(2) Working substance : Steam, petrol etc.
(3) Sink: It is a reservoir of heat at low temperature and infinite thermal capacity. Any amount of heat can be given to the sink.
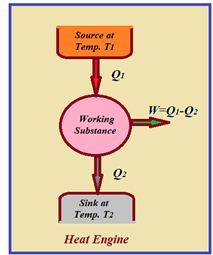
The working substance absorbs heat Q1 from the source, does an amount of work W, returns the remaining amount of heat to the sink and comes back to its original state and there occurs no change in its internal energy.
By repeating the same cycle over and over again, work is continuously obtained.
The performance of heat engine is expressed by means of “efficiency” h which is defined as the ratio of useful work obtained from the engine to the heat supplied to it.
\eta =\frac{{\text{Work done}}}{{\text{Heat input}}}=\frac{W}{{{{Q}_{1}}}}
For cyclic process DU = 0 hence from first law of thermodynamicsDQ = DW
So W={{Q}_{1}}-{{Q}_{2}}Þ \eta =\frac{{{{Q}_{1}}-{{Q}_{2}}}}{{{{Q}_{1}}}}=1-\frac{{{{Q}_{2}}}}{{{{Q}_{1}}}}
A perfect heat engine is one which converts all heat into work i.e. W={{Q}_{1}} so that {{Q}_{2}}=0 and hence {{Q}_{2}}=0.
But practically efficiency of an engine is always less than 1.
Refrigerator or Heat Pump
A refrigerator or heat pump is basically a heat engine run in reverse direction.
It essentially consists of three parts
(1) Source : At higher temperature T1.
(2) Working substance : It is called refrigerant liquid ammonia and freon works as a working substance.
(3) Sink : At lower temperature T2.
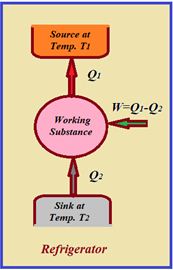
The working substance takes heat Q2 from a sink (contents of refrigerator) at lower temperature, has a net amount of work done W on it by an external agent (usually compressor of refrigerator) and gives out a larger amount of heat Q1 to a hot body at temperature T1 (usually atmosphere). Thus, it transfers heat from a cold to a hot body at the expense of mechanical energy supplied to it by an external agent. The cold body is thus cooled more and more.
The performance of a refrigerator is expressed by means of “coefficient of performance” COP which is defined as the ratio of the heat extracted from the cold body to the work needed to transfer it to the hot body.
i.e. COP=\frac{{\text{Heat extracted}}}{{\text{Work done}}}=\frac{{{{Q}_{2}}}}{W}=\frac{{{{Q}_{2}}}}{{{{Q}_{1}}-{{Q}_{2}}}}
(1) Carnot refrigerator :
For Carnot refrigerator \frac{{{{Q}_{1}}}}{{{{Q}_{2}}}}=\frac{{{{T}_{1}}}}{{{{T}_{2}}}}
\frac{{{{Q}_{1}}-{{Q}_{2}}}}{{{{Q}_{2}}}}=\frac{{{{T}_{1}}-{{T}_{2}}}}{{{{T}_{2}}}} or \frac{{{{Q}_{2}}}}{{{{Q}_{1}}-{{Q}_{2}}}}=\frac{{{{T}_{2}}}}{{{{T}_{1}}-{{T}_{2}}}}
So coefficient of performance =\frac{{{{T}_{2}}}}{{{{T}_{1}}-{{T}_{2}}}}
where T1 = temperature of surrounding, T2 = temperature of cold body.
(2)
Relation between coefficient of performance and efficiency of refrigerator
We know COP=\frac{{{{Q}_{2}}}}{{{{Q}_{1}}-{{Q}_{2}}}} =\frac{{{{Q}_{2}}/{{Q}_{1}}}}{{1-{{Q}_{2}}/{{Q}_{1}}}} ….. (i)
But the efficiency \eta =1-\frac{{{{Q}_{2}}}}{{{{Q}_{1}}}} or \frac{{{{Q}_{2}}}}{{{{Q}_{1}}}}=1-\eta …..(ii)
From (i) and (ii) we get, COP=\frac{{1-\eta }}{\eta }
Carnot Engine
1.
Carnot designed a theoretical engine which is free from all the defects of a practical engine. This engine cannot be realised in actual practice, however, this can be taken as a standard against which the performance of an actual engine can be judged.
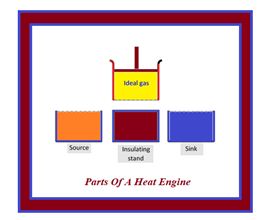
It consists of the following parts
(i) A cylinder with perfectly non-conducting walls and a perfectly conducting base containing a perfect gas as working substance and fitted with a non-conducting frictionless piston
(ii) A source of infinite thermal capacity maintained at constant higher temperature T1.
(iii) A sink of infinite thermal capacity maintained at constant lower temperature T2.
(iv) A perfectly non-conducting stand for the cylinder.
(2)
Carnot cycle : As the engine works, the working substance of the engine undergoes a cycle known as Carnot cycle. The Carnot cycle consists of the following four strokes
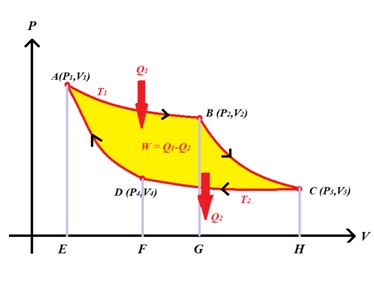
(i) First stroke (Isothermal expansion) (curve AB) : The Source at temperature T1 is kept in contact with the cylinder znd heat is supplied slowly as a result the cylinder containing ideal gas as working substance allowed to expand slowly at this constant temperature T1 from state A to B
Work done = Heat absorbed by the system
{{W}_{1}}={{Q}_{1}}=\int_{{\,{{V}_{1}}}}^{{\,{{V}_{2}}}}{{P\,dV}}=R{{T}_{1}}{{\log }_{e}}\left( {\frac{{{{V}_{2}}}}{{{{V}_{1}}}}} \right)=Area ABGE
(ii) Second stroke (Adiabatic expansion) (curve BC) : The source is removed and the cylinder is then placed on the non conducting stand and the gas is allowed to expand adiabatically till the temperature falls from T1 to T2 that is from state B to C
{{W}_{2}}=\int_{{\,{{V}_{2}}}}^{{\,{{V}_{3}}}}{{P\,dV}}= \frac{R}{{(\gamma -1)}}[{{T}_{1}}-{{T}_{2}}]=Area BCHG
(iii) Third stroke (Isothermal compression) (curve CD) :
The cylinder is placed on the sink and the gas is compressed at constant temperature T2 from state C to D
Work done = Heat released by the system
{{W}_{3}}={{Q}_{2}}=-\int_{{\,{{V}_{3}}}}^{{\,{{V}_{4}}}}{{\,P\,dV}}=-R{{T}_{2}}{{\log }_{e}}\frac{{{{V}_{4}}}}{{{{V}_{3}}}}
=R{{T}_{2}}{{\log }_{e}}\frac{{{{V}_{3}}}}{{{{V}_{4}}}}=\text{Area }CDFH\,
(iv) Fourth stroke (adiabatic compression) (curve DA) : The sink is removed and Finally the cylinder is again placed on non-conducting stand and the compression is continued so that gas returns to its initial state A
{{W}_{4}}=-\int_{{\,{{V}_{4}}}}^{{\,{{V}_{1}}}}{{P\,dV}}=-\frac{R}{{\gamma -1}}({{T}_{2}}-{{T}_{1}}) =\frac{R}{{\gamma -1}}({{T}_{1}}-{{T}_{2}})=\text{Area }ADFE
(3) Efficiency of Carnot cycle : The efficiency of engine is defined as the ratio of work done to the heat supplied i.e. \eta =\frac{{\text{Work done}}}{{\text{Heat input}}}=\frac{W}{{{{Q}_{1}}}}
Net work done during the complete cycle
W={{W}_{1}}+{{W}_{2}}+(-{{W}_{3}})+(-{{W}_{4}}) ={{W}_{1}}-{{W}_{3}}=\text{Area }ABCD
[As {{W}_{2}}={{W}_{4}}]
\eta =\frac{W}{{{{Q}_{1}}}}=\frac{{{{W}_{1}}-{{W}_{3}}}}{{{{W}_{1}}}}=\frac{{{{Q}_{1}}-{{Q}_{2}}}}{{{{Q}_{1}}}}=1-\frac{{{{W}_{3}}}}{{{{W}_{1}}}}=1-\frac{{{{Q}_{2}}}}{{{{Q}_{1}}}}
or \eta =1-\frac{{R{{T}_{2}}{{{\log }}_{e}}({{V}_{3}}/{{V}_{4}})}}{{R{{T}_{1}}{{{\log }}_{e}}({{V}_{2}}/{{V}_{1}})}} —— (1)
Since points B and C lie on same adiabatic curve so we can apply the equation of adiabatic process from B to C
\ {{T}_{1}}V_{2}^{{\gamma -1}}={{T}_{2}}V_{3}^{{\gamma -1}} or \frac{{{{T}_{1}}}}{{{{T}_{2}}}}={{\left( {\frac{{{{V}_{3}}}}{{{{V}_{2}}}}} \right)}^{{\gamma -1}}} …..(2)
Also point D and A lie on the same adiabatic curve
\ {{T}_{1}}V_{1}^{{\gamma -1}}={{T}_{2}}V_{4}^{{\gamma -1}} or \frac{{{{T}_{1}}}}{{{{T}_{2}}}}={{\left( {\frac{{{{V}_{4}}}}{{{{V}_{1}}}}} \right)}^{{\gamma -1}}} …..(3)
From (2) and (3), \frac{{{{V}_{3}}}}{{{{V}_{2}}}}=\frac{{{{V}_{4}}}}{{{{V}_{1}}}} or \frac{{{{V}_{3}}}}{{{{V}_{4}}}}=\frac{{{{V}_{2}}}}{{{{V}_{1}}}}Þ \frac{{{{V}_{3}}}}{{{{V}_{4}}}}=\frac{{{{V}_{2}}}}{{{{V}_{1}}}}
So from equation (1) the efficiency of Carnot engine \eta =1-\frac{{{{T}_{2}}}}{{{{T}_{1}}}}
(i) Efficiency of a heat engine depends only on temperatures of source and sink and is independent of all other factors.
(ii) All reversible heat engines working between same temperatures are equally efficient and no heat engine can be more efficient than Carnot engine (as it is ideal).
(iii) As on Kelvin scale, temperature can never be negative (as 0 K is defined as the lowest possible temperature) and Tl and T2 are finite, efficiency of a heat engine is always lesser than unity, i.e., whole of heat can never be converted into work which is in accordance with second law.
(iv) Carnot stated that no heat engine working between two given temperatures of source and sink can be more efficient than a perfectly reversible engine (Carnot engine) working between the same two temperatures. Carnot’s reversible engine working between two given temperatures is considered to be the most efficient engine.
Illustration
P–T curve of the following process will be
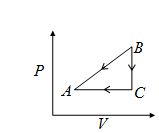
in process AB,\ \ \ \ V\propto P
V=kP
PV=nRT
T=\frac{k}{{nR}}{{p}^{2}}, parabolic
∴ (b)
Illustration
Temperature of source is 330ºC. Temperature of sink is changed in order to increase the efficiency of engine from 1/5 to1/4, by
(a) 30ºK
(b) 303 K
(c) 603 K
(d) 60 K
Solution
\eta =1-\frac{{{{T}_{2}}}}{{{{T}_{1}}}}
\frac{1}{5}=1-\frac{{{{T}_{2}}}}{{{{T}_{1}}}}
\frac{1}{4}=1-\frac{{T{{‘}_{2}}}}{{{{T}_{1}}}}
\frac{{{{T}_{2}}-T{{‘}_{2}}}}{{{{T}_{1}}}}=\frac{1}{4}-\frac{1}{5}=\frac{1}{{20}}
\Delta {{T}_{2}}=\frac{1}{{20}}\times (330+273)=30.15{}^\text{o}K
∴ (a)
Practice Questions (Basic Level)
1.
A Carnot engine is working between 127°C and 27°C. The increase in efficiency will be maximum when the temperature of
(a) the source is increased by 50°C
(b) the sink is decreased by 50°C
(c) source is increased by 25°C and that of sink is decreased by 25°C
(d) both source and sink are decreased by 25°C each
Ans (b)
2.
Three moles of an ideal monoatomic gas undergoes the process ABCDA as shown, where {{T}_{A}}\ =\ 300K, {{T}_{B}}\ =\ 600K, {{T}_{c}}\ =\ 1800\ Kand {{T}_{D}}\ =\ 900\ K. Find the work done by the gas during the cycle.
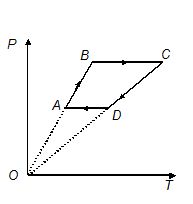
(a) 17.8 kJ
(b) 14.9 kJ
(c) 19.9 kJ
(d) 21.1 kJ
Ans (b)
3.
A thermo dynamical system goes from state (i) {{P}_{1}},\,Vto 2{{P}_{1}},\,V (ii) P, V to P, 2V. Then work done in the two cases is
(a) zero, zero
(b) zero, PV
(c) P{{V}_{1}}, zero
(d) P{{V}_{1}}, {{P}_{1}}{{V}_{1}}
Ans(b)
4.
An ideal gas is taken through series of changes represented in fig. The net work done by the gas at the end of the cycle is equal to
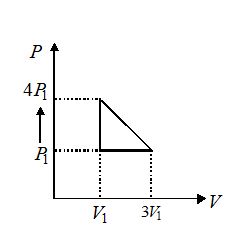
(a) {{P}_{1}}{{V}_{1}}
(b) 3{{P}_{1}}{{V}_{1}}
(c) 6{{P}_{1}}{{V}_{1}}
(d) 12{{P}_{1}}{{V}_{1}}
Ans (d)
5.
Heat energy absorbed by a system in going through a cyclic process shown in figure is

(a) {{10}^{7}}\pi J
(b) {{10}^{4}}\pi J
(c) {{10}^{2}}\pi J
(d) {{10}^{{-3}}}\pi J
Ans (c)
6.
An ideal gas is taken through the cycle A→B→C→A, as shown in the figure. If the net heat supplied to the gas in the cycle is 5 J, the work done by the gas in the process C→A is
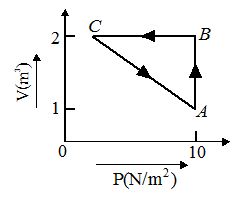
(a) –5 J
(b) –10 J
(c) –15J
(d) –20 J
Ans(a)
Practice Questions (JEE Main Level)
1.
A fixed mass of gas undergoes the cycle of changes represented by PQRSP as shown in figure. In some of the changes, work is done on the gas and in other; work is done by the gas. In which pair of the changes is work done on the gas?
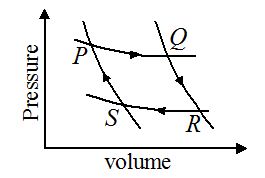
(a) PQ and RS
(b) QR and RS
(c) RS and SP
(d) PQ and QR
Ans (c)
2.
The first operation involved in a Carnot cycle is
(a) isothermal expansion
(b) adiabatic expansion
(c) isothermal compression
(d) adiabatic compression
Ans (a)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
