Video Lecture
Theory For Making Notes
Thermodynamics is a branch of science which deals with exchange of heat energy between bodies and conversion of the heat energy into mechanical energy and vice-versa.
Few Important Terms Used In Thermodynamics
(1)
Thermodynamic system
(i) It is a collection of an extremely large number of atoms or molecules normally a gas
(ii) It is confined with in certain boundaries.
(iii) Anything outside the thermodynamic system to which energy or matter is exchanged is called its surroundings.
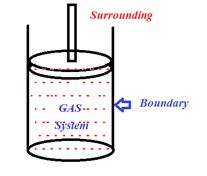
(iv) Thermodynamic system may be of three types
(a) Open system : It exchange both energy and matter with the surrounding.
(b) Closed system : It exchange only energy (not matter) with the surroundings.
(c) Isolated system : It exchange neither energy nor matter with the surrounding.
(2)
Thermodynamic coordinates / variables:
A thermodynamic system can be described by specifying its pressure, volume, temperature, internal energy and the number of moles. These parameters are called thermodynamic variables or coordinates. The relation between the thermodynamic variables (P, V, T) of the system is called equation of state.
For n moles of an ideal gas, equation of state is PV = nRT.
(3)
Thermodynamic equilibrium :
A system is said to be in the state of thermodynamic equilibrium when its thermodynamic variables remains fixed or constant and does not change with time. For a system to be in thermodynamic equilibrium, the following conditions must be fulfilled.
(i) Thermal equilibrium : There is a uniform temperature in all parts of the system and is same as that of surrounding.
(ii) Mechanical equilibrium : There is no unbalanced force between the system and its surroundings.
(iii) Chemical equilibrium : There is a uniform chemical composition through out the system and the surrounding.
(4)
Thermodynamic process :Any activity or occurrence of change of state of a system involving change of thermodynamic coordinates like pressure P, volume V and temperature T of the system is known as thermodynamic process. Some important processes are
(i) Isochoric process : Volume remains constant
(ii) Isobaric process : Pressure remains constant
(iii) Isothermal process : Temperature remain constant
(iv) Adiabatic process : No transfer of heat
(v) Cyclic and non-cyclic process : In a cyclic process Initial and final states are same while in non-cyclic process these states are different.
(vi) Reversible and irreversible process :
(5)
Indicator diagram :Whenever the state of a gas (P, V, T) is changed, we say the gaseous system is undergone a thermodynamic process. The graphical representation of the change in state of a gas by a thermodynamic process is called indicator diagram. Indicator diagram is plotted generally in pressure and volume of gas.
Zeroth Law of Thermodynamics
If systems A and B are each in thermal equilibrium with a third system C,then A and B are in thermal equilibrium with each other.
The zeroth law leads to the concept of temperature. All bodies in thermal equilibrium must have a common property which has the same value for all of them. This property is called the temperature.
First Law of Thermodynamics
(1) It is a statement of conservation of energy in thermodynamic process.
(2) According to it heat given to a system (DQ) is equal to the sum of increase in its internal energy (DU) and the work done (DW) by the system against the surroundings.
\displaystyle \Delta Q=\Delta W+\Delta U
(3) It makes no distinction between work and heat as according to it the internal energy (and hence temperature) of a system may be increased either by adding heat to it or doing work on it or both.
(4) ΔQ and ΔW are the path functions but ΔU is the point function.
(5) In the above equation all three quantities ΔQ, ΔU and ΔW must be expressed either in Joule or in calorie.
(6) The first law introduces the concept of internal energy.
(7) First law of thermodynamics does not indicate the direction of heat transfer. It does not tell anything about the conditions, under which heat can be transformed into work and also it does not indicate as to why the whole of heat energy cannot be converted into mechanical work continuously.
Sign convention in thermodynamics
Quantity | Sign | Condition |
ΔQ | + | When heat is supplied to a system |
– | When heat is drawn from the system | |
ΔW | + | When work done by the gas (expansion) |
– | When work done on the gas (compression) | |
ΔU | + | With temperature rise, internal energy increases |
– | With temperature fall, internal energy decreases |
Isobaric Process
When a thermodynamic system undergoes a physical change in such a way that its pressure remains constant, then the change is known as isobaric process.
Examples of isobaric process :All process occuring in open atmosphere like steam formation from boiling water in an open vessel.
(1) Equation of state :In this process V and T changes but P remains constant. Hence Charle’s law is obeyed in this process.
Hence if pressure remains constant V∝T⇒ \frac{{{{V}_{1}}}}{{{{T}_{1}}}}=\frac{{{{V}_{2}}}}{{{{T}_{2}}}}
(2) Its P-V Graph is a horizontal line along volume axis. The diagram given below represents an isobaric expansion. Area under the graph represents the work done on the system or by the system.
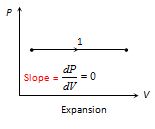
(3) Specific heat :Specific heat of gas during isobaric process {{C}_{P}}=\left( {\frac{f}{2}+1} \right)R.Where f is degree of freedom without vibration.
(4) Bulk modulus of elasticity : K=\frac{{\Delta P}}{{\frac{{-\Delta V}}{V}}}=0 [As DP = 0]
(5) Work done in isobaric process
\Delta W=\int_{{{{V}_{i}}}}^{{{{V}_{f}}}}{{P\,dV}}=P\int_{{{{V}_{i}}}}^{{{{V}_{f}}}}{{dV}}=P[{{V}_{f}}-{{V}_{i}}] [As P is constant so it is taken out of integration]
hence \Delta W=P({{V}_{f}}-{{V}_{i}})=\mu R[{{T}_{f}}-{{T}_{i}}]=\mu R\,\Delta T
(6) Heat transfer in isobaric process : From \Delta Q=\Delta U+\Delta W
\Delta U=\mu \,{{C}_{V}}\,\Delta T and \Delta W=\mu R\,\Delta T
{{(\Delta Q)}_{P}}=\mu {{C}_{v}}\Delta T+\mu R\,\Delta T \mu \,({{C}_{v}}+R)\,\Delta T=\mu \,{{C}_{P}}\,\Delta T
Isochoric Process
When a thermodynamic process undergoes a physical change in such a way that its volume remains constant, then the change is known as isochoric process. It happens when the boundaries of the system remains fix.
(1) Equation of state :In this process P and T changes but V = constant. Hence Gay-Lussac’s law is obeyed in this process i.e.P µTÞ \frac{{{{P}_{1}}}}{{{{T}_{1}}}}=\frac{{{{P}_{2}}}}{{{{T}_{2}}}}= constant
(2) P-V graph :For this process this graph is a straight line parallel to pressure axis.
The graph given below represents an isochoric process involving increase in pressure at volume and slope graph \frac{{dP}}{{dV}}=\infty
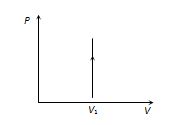
3) Specific heat : Specific heat of gas during isochoric process {{C}_{V}}=\frac{f}{2}R. Where f is degree of freedom without vibration.
(4) Bulk modulus of elasticity : K=\frac{{\Delta P}}{{\frac{{-\Delta V}}{V}}}=\frac{{\Delta P}}{0}=\infty
(5) Work done in isochoric process
\Delta W=P\Delta V=P[{{V}_{f}}-{{V}_{i}}]= 0 [As V = constant]
(6) Heat transfer in isochoric process : From \Delta Q=\Delta U+\Delta W
DW = 0
therefore {{(\Delta Q)}_{V}}=\Delta U=\mu \,{{C}_{V}}\,\Delta T =\mu \frac{R}{{\gamma -1}}\Delta T =\frac{{{{P}_{f}}{{V}_{f}}-{{P}_{i}}{{V}_{i}}}}{{\gamma -1}}.
Isothermal Process
When a thermodynamic system undergoes a physical change in such a way that its temperature remains constant, then the change is known as isothermal changes.
Example of isothermal process : Any process involving phase change like Melting of ice (at 0°C) and boiling of water (at 100°C)
(1) Essential condition for isothermal process
(i) The walls of the container must be perfectly conducting to allow free exchange of heat between the gas and its surrounding.
(ii) The process of compression or expansion should be so slow so as to provide time for the exchange of heat.
Since these two conditions are not fully realised in practice, therefore, no process is perfectly isothermal.
(2) Equation of state :In this process, P and V change but T = constant i.e. change in temperature DT = 0.
Boyle’s law is obeyed i.e.PV= constant P1V1 = P2V2
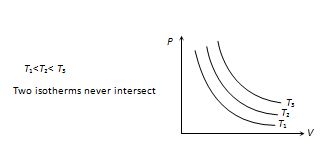
(4) Indicator diagram : According to PV = constant, graph between P and V is a part of rectangular hyperbola. The graphs at different temperature are parallel to each other are called isotherms.
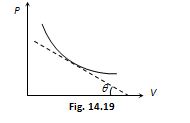
Slope of isothermal curve :By differentiating PV = constant. On differentiation we get
P\,dV+V\,dP=0
PdV=\,-\,VdP
Slope = \tan \theta =\frac{{dP}}{{dV}}=-\frac{P}{V}
(5) Work done in isochoric process
we know thatPV =nRT
But un isothermal process nRT is a constant say equal to `c’ hence c= nRT
therefore \displaystyle P=\frac{c}{V}.
hencework done in an isothermal process is given by
W = \displaystyle \int\limits_{{{{V}_{i}}}}^{{{{V}_{f}}}}{{PdV}}=c\int\limits_{{{{V}_{i}}}}^{{{{V}_{f}}}}{{\frac{{dV}}{V}}}=c\left[ {\ln (V)} \right]_{{{{V}_{i}}}}^{{{{V}_{f}}}}
Hence \displaystyle \Delta Q=\Delta W+\Delta U
\displaystyle W=c\left[ {\ln ({{V}_{f}})-({{V}_{i}})} \right]=c\ln \left( {\frac{{{{V}_{f}}}}{{{{V}_{i}}}}} \right)
Therefore \displaystyle W=nRT\ln \left( {\frac{{{{V}_{f}}}}{{{{V}_{i}}}}} \right)
Also \displaystyle W=nRT\ln \left( {\frac{{{{P}_{i}}}}{{{{P}_{f}}}}} \right)
(6) Specific heat : Specific heat of gas during isothermal change is infinite. As C=\frac{Q}{{m\Delta T}}=\frac{Q}{{m\times 0}}=\infty [As ΔT = 0]
(7) Isothermal elasticity (Eq) : For this process PV = constant.
Þ P\,dV=-V\,dP Þ P=-\frac{{VdP}}{{dV}}=B\text{(Bulk Modulus)}
so isothermal elasticity (here Bulk Modulus) is equal to pressure
(8)Heat transfer in isothermal process : From \Delta Q=\Delta U+\Delta W
\Delta U=0
[As DT = 0] \Delta Q=\Delta W hence \displaystyle \Delta Q=nRT\ln \left( {\frac{{{{P}_{i}}}}{{{{P}_{f}}}}} \right)
i.e. heat supplied in an isothermal change is used to do work against external surrounding.
or if the work is done on the system than equal amount of heat energy will be liberated by the system.
Adiabatic Process
When a thermodynamic system undergoes a change in such a way that no exchange of heat takes place between System and surroundings, the process is known as adiabatic process. Hence In this process P, V and T changes but ΔQ = 0. The essential conditions for adiabatic process is that all walls of the container and the piston must be perfectly insulating and also the system should be compressed or allowed to expand suddenly so that there is no time for the exchange of heat between the system and its surroundings.Since, these two conditions are not practically possible therefore no process can be perfectly adiabatic.
Examples of adiabatic process
(i) Sudden compression or expansion of a gas in a container with perfectly non-conducting walls.
(ii) burst of the tube of a tyre
(iii) Propagation of sound waves agaseous medium.
(iv) Expansion of steam in the cylinder of steam engine.
Adiabatic expansion or compression causes cooling and heating
From \Delta Q=\Delta U+\Delta W
For adiabatic process \Delta Q=0 Þ \Delta U=-\,\Delta W
If ΔW = positive that is work is done by the system then ΔU = negative so temperature decreases i.e. adiabatic expansion produce cooling.
If ΔW = negative that is work is done ohn the system then ΔU = positive so temperature increases i.e. adiabatic compression produce heating.
Equation of process : In adiabatic change ideal gases obeys Poisson’s law. According to it
PV = constant; where \gamma =\frac{{{{C}_{P}}}}{{{{C}_{V}}}}
Hence the equation of adiabatic process can be expressed in three ways
(i)
In terms of pressure and volume as \displaystyle P{{V}^{\gamma }} = constant
(ii)
In terms of temperature and volume TVg – 1 = constant
(iii)
In terms of temperature and pressure \frac{{{{T}^{\gamma }}}}{{{{P}^{{\gamma -1}}}}} = constant
(1)
Indicator diagram
The curve obtained on PV graph is called adiabatic curve.Slope of adiabatic curve can be obtained by differentiating the equation of the process P{{V}^{\gamma }}=\text{constant}
By differentiating, we get
dP\,{{V}^{\gamma }}+P\gamma {{V}^{{\gamma -1}}}\,dV=0
\frac{{dP}}{{dV}}=-\gamma \frac{{P{{V}^{{\gamma -1}}}}}{{{{V}^{\gamma }}}}=-\gamma \left( {\frac{P}{V}} \right)
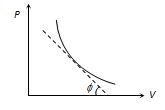
Slope of adiabatic curve \tan \varphi =-\gamma \left( {\frac{P}{V}} \right)
whereas the slope of isothermal curve \tan \theta =\frac{{-P}}{V}
Hence (Slope)Adi = g´ (Slope)Iso or \frac{{{{{(\text{Slope)}}}_{{Adi}}}}}{{{{{(\text{Slope)}}}_{{Iso}}}}}>1 due to this the adiabatic curve is more steeper than the isothermal curve as shown in the figure
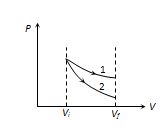
Here 1st curve represent the isothermal expansion and 2nd curve represent the adiabatic expansion
(2) Specific heat : Specific heat of a gas during adiabatic change is zero As C=\frac{{\Delta Q}}{{m\Delta T}}=\frac{0}{{m\Delta T}}=0 [As \displaystyle \Delta Q=0]
(3) Adiabatic elasticity:
(i) \displaystyle W=\frac{{\mu R({{T}_{i}}-{{T}_{f}})}}{{(\gamma -1)}}{{P}_{i}}V_{i}^{{^{{1-\gamma }}}}={{P}_{f}}V_{f}^{{^{{1-\gamma }}}}=C
P{{V}^{\gamma }}=\text{constant}
Differentiating both sides d\,P{{V}^{\gamma }}+P\gamma {{V}^{{\gamma -1}}}dV=0
\Rightarrow \gamma P=\frac{{dP}}{{-dV/V}}=B ( Bulk Modulus)
so adiabatic elasticity (here Bulk Modulus) is gtimes that of pressure P
whereas the isothermal elasticity ( Bulk modulus) B=P
(4) Work done in adiabatic process
W=\int_{{{{V}_{i}}}}^{{{{V}_{f}}}}{{P\,dV}} ( From equation of process \displaystyle P=\frac{C}{{{{V}^{\gamma }}}})
\Rightarrow C\int_{{{{V}_{i}}}}^{{{{V}_{f}}}}{{\frac{{dV}}{{{{V}^{\gamma }}}}}}
\displaystyle C\left( {\frac{{{{V}^{{1-\gamma }}}}}{{1-\gamma }}} \right)_{{{{V}_{i}}}}^{{{{V}_{f}}}}
\displaystyle \Rightarrow C\left( {\frac{{V_{f}^{{^{{1-\gamma }}}}-V_{i}^{{^{{1-\gamma }}}}}}{{1-\gamma }}} \right)
\displaystyle \Rightarrow \left( {\frac{{CV_{f}^{{^{{1-\gamma }}}}-CV_{i}^{{^{{1-\gamma }}}}}}{{1-\gamma }}} \right) (from equation of process \displaystyle {{P}_{i}}V_{i}^{{^{\gamma }}}={{P}_{f}}V_{f}^{{^{\gamma }}}=C)
\displaystyle \Rightarrow \left( {\frac{{({{P}_{f}}V_{f}^{{^{\gamma }}})V_{f}^{{^{{1-\gamma }}}}-({{P}_{i}}V_{i}^{\gamma })V_{i}^{{^{{1-\gamma }}}}}}{{1-\gamma }}} \right)
hence W=\frac{{[{{P}_{i}}{{V}_{i}}-{{P}_{f}}{{V}_{f}}]}}{{(\gamma -1)}}
Also this can be expressed in terms of temperature as \displaystyle W=\frac{{nR({{T}_{i}}-{{T}_{f}})}}{{(\gamma -1)}}
Illustration
Calculate the fall in temperature of helium initially at 15°C, when it is suddenly expanded to 8 times its original volume (\gamma =5/3).
Solution
Here, (\gamma =5/3);
{{T}_{2}}=?
{{V}_{2}}=8{{V}_{1}},\,\,\,\gamma =5/3
As, {{T}_{2}}\,V_{2}^{{\gamma -1}}={{T}_{1}}\,V_{1}^{{\gamma -1}}
{{T}_{2}}={{T}_{1}}{{\left( {\frac{{{{V}_{1}}}}{{{{V}_{2}}}}} \right)}^{{\gamma -1}}}=288{{\left( {\frac{{{{V}_{1}}}}{{8{{V}_{1}}}}} \right)}^{{5/3-1}}}
or \log {{T}_{2}}=\log 288+\frac{2}{3}\log \left( {\frac{1}{8}} \right) =\log 288+\frac{2}{3}[\log 1-\log 8]
\log {{T}_{2}}=2.4594+\frac{2}{3}[0-0.9031]\,\,=1.8573
{{T}_{2}}=antilog 1.8573 = 71.99 K
fall in temperature of helium
{{T}_{1}}-{{T}_{2}}=288-71.99\,\,\,\,=216.01\,\,K
=216.01{}^\circ C in magnitude, 1{}^\circ C\,=1K)
Illustration
A gas is suddenly compressed to 1/4th of its original volume. Calculate the rise in temperature, the original temperature being 27°C and \gamma =1.5.
Solution:
Let the initial volume, {{V}_{1}}=V
Final volume, {{V}_{2}}=V/4
Here, initial temperature, {{T}_{1}}=27{}^\circ C\,\,\,\,\,=273+27=300\,Kand \gamma =1.5
Let {{T}_{2}} be the final temperature after compression.
Since, the change is adiabatic,
{{T}_{1}}\,\,V_{1}^{{\gamma -1}}={{T}_{2}}\,\,V_{2}^{{\gamma -1}}
or {{T}_{2}}={{T}_{1}}{{\left( {\frac{{{{V}_{1}}}}{{{{V}_{2}}}}} \right)}^{{\gamma -1}}}=300{{\left[ {\frac{V}{{V/4}}} \right]}^{{1.5-1}}}
=300{{(4)}^{{1/2}}}=300\times 2=600K
{{T}_{2}}=600-273=327{}^\circ C
rise in temperature =327{}^\circ C-27{}^\circ C\,\,\,=300{}^\circ C or 300 K.
Illustration
A gram molecule of a gas at 127°C expands isothermally until its volume is doubled. Find the amount of work done and heat absorbed.
Solution:
Here, temperature of the gas T=273+127=400K
Let initial volume of the gas, {{V}_{1}}=V
final volume of the gas, {{V}_{2}}=2V
In an isothermal expansion,
Work done (W) =2.3026RT{{\log }_{{10}}}\frac{{{{V}_{2}}}}{{{{V}_{1}}}}
=2.3026\times 8.3\times 400\times {{\log }_{{10}}}\frac{{2V}}{V}
=2.3026\times 8.3\times 400\times 0.3010
or W=2.30\times {{10}^{3}}\,\,Joule
If H is the amount of heat absorbed, H=\frac{W}{J}=\frac{{2.303\times {{{10}}^{3}}}}{{4.2}}=548\,\,cal.
Illustration
One mole of an ideal gas undergoes a cyclic change ABCD. From the given diagram, calculate the net work done in the process.
1 atmosphere ={{10}^{6}}\,\,dyne\,\,\,c{{m}^{{-2}}}.
Solution:
In a cyclic change, work done in equal to area of the loop ABCD representing the change, shown in figure.
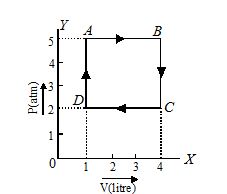
As the loop is treaced in clockwise direction, work done is positive,
W=area ABCDA = DC × DA
Now, DC=4-1=3litre =3\times {{10}^{3}}\,\,c{{m}^{3}}
DA=5-2=3\,\,atm =3\times {{10}^{6}}\,\,dyne\,\,\,c{{m}^{{-2}}}
W=DC\times DA
=3\times {{10}^{3}}\times 3\times {{10}^{6}}
=9\times {{10}^{9}}\,\,erg
Illustration
A mass of 8 g of oxygen at the pressure of one atmosphere and at temperature 27o is enclosed in a cylinder fitted with a frictionless piston. The following operations are performed in the order given:
(A) The gas is heated at constant pressure to 127oC,
(B) Then it is compressed isothermally to its initial volume and
(C) Finally it is cooled to its initial temperature at constant volume.
(a) What is the heat absorbed by the gas during operation (a)?
(b) How much work is done by the gas in state (a)?
(c) What is the work done on the gas in stage (B)?
(d) How much heat is extracted from the gas in stage (C)?
[Specific heat capacity of oxygen Cv = 670 J/kg K;
Molecular weight of oxygen = 32; 1 atm = 1.013 x 105 N/m2]
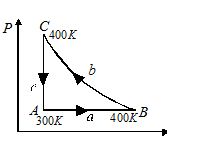
{{V}_{A}}\,=\,\,\frac{8}{{32}}\,\,\times \,\,22.4\,\,\times \,\,\frac{{300}}{{\,273}}\,\,\,\,\,\mathbf{litr}{{\mathbf{e}}_{{\,\,}}} =\,\frac{{560}}{{91}}\,\,\times \,\,{{10}^{{-3}}}{{m}^{3}}
{{V}_{B}}={{V}_{A}}\,\times \frac{{400}}{{300}}=\frac{4}{3}{{V}_{A}}
{{V}_{B}}-{{V}_{A}}=\frac{1}{3}{{V}_{A}}
(a)
dQ = dU + dW = mCv \displaystyle \Delta T + p( {{V}_{B}}-{{V}_{A}})
= \frac{8}{{1000}}\,\,\times \,\,670\,\,\times \,100+1.013\,\,\times \,\,{{10}^{5}}\times \,\,\left[ {\frac{{560\,\times \,{{{10}}^{{-3}}}}}{{3\,\times \,91}}} \right]=536+207.8 = 743.8 J
(b)
dW = p( {{V}_{B}}-{{V}_{A}}) = 207.8 J
(c)
Work done in compressing the gas isothermally = \frac{m}{M}RT\,\,{{\log }_{e}}\frac{{{{V}_{B}}}}{{{{V}_{A}}}}
= \frac{8}{{32}}\,\,\times \,\,\,8.31\,\,\times \,\,400\,\,\,{{\log }_{e}}\frac{4}{3} = 831× 0.2877 = 1 J
(d)
Heat given out by the gas in stage (c) = m{{C}_{v}}\Delta T=\frac{8}{{1000}}\,\times \,\,670\,\,\times \,\,100= 536 J
Illustration
Two moles of an ideal gas at 300 K were cooled at constant volume so that the pressure is reduced to half the initial value. Then as a result of heating at constant pressure the gas has expanded till it attains the original temperature. The total heat absorbed by gas, if R is the gas constant
(a) 150R
(b) 300R
(c) 75R
(d) 100R
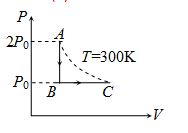
n = 2 moles, {{T}_{A}}={{T}_{C}}=300K
For isochoric process AB,
{{(\Delta Q)}_{{AB}}}={{U}_{B}}-{{U}_{A}}=n{{C}_{V}}({{T}_{B}}-{{T}_{A}})= –300 CV
For isobaric process BC,
{{(\Delta Q)}_{{BC}}}=n{{C}_{P}}({{T}_{C}}-{{T}_{B}})=300\,{{C}_{P}}
\Delta Q=\Delta {{Q}_{{AB}}}+\Delta {{Q}_{{BC}}}=300\left( {{{C}_{P}}-{{C}_{V}}} \right)=300R
∴ (b)
Illustrtation
One mole of an ideal monatomic gas is taken from temperature T0 to 2T0 by the process
PT–4 = C. Considering the following statements. Choose the correct alternative.
1.
Molar heat capacity of the gas is -\frac{{3R}}{2}
2.
Molar heat capacity of the gas is \frac{{3R}}{2}
3.
Work done is -3R{{T}_{0}}
4.
Work done is 3R{{T}_{0}}
(a) Statements I and IV are correct.
(b) Statements I and III are correct.
(c) Statements II and IV are correct.
(d) Statements II and III are correct.
Solution
We know that P{{T}^{{-4}}}=C,\,\,P{{V}^{{4/3}}}=C
C=\frac{R}{{\gamma -1}}-\frac{R}{{x-1}}=\frac{{3R}}{2}-\frac{{3R}}{1}=\frac{{-3R}}{2}
W=\frac{{\eta R({{T}_{1}}-{{T}_{2}})}}{{\frac{4}{3}-1}}=-3R{{T}_{0}}
∴ (b)
Illustration
A gas is expanded from volume V0 to 2V0 under three different processes. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1, ΔU2 and ΔU3 be the change in internal energy of the gas in these three processes. Then
(a) ΔU1>ΔU2>ΔU3
(b) ΔU1<ΔU2>ΔU3
(c) ΔU2<ΔU1<ΔU3
(d) ΔU2>ΔU3>ΔU1
Solution
Process 2 is an isothermal process.
Hence, ΔU2 = 0.
Process 1 is an isobaric (P = constant) expansion.
Hence, temperature of the gas will increase.
or \Delta {{U}_{1}}=\text{positive}
Process 3 is an adiabatic expansion. Hence, temperature will decrease;
or \Delta {{U}_{3}}=\text{negative}
Therefore, ΔU1>ΔU2>ΔU3 is the correct option.
∴ (a)
Practice Questions (Basic Level)
1.
An ideal gas of mass in a state A goes to another state B via three different processes as shown in figure. If {{Q}_{1}},\,{{Q}_{2}} and {{Q}_{3}} denote the heat absorbed by the gas along the three paths, then
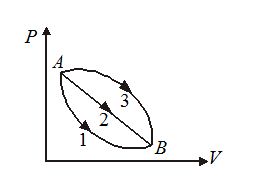
(a) {{Q}_{1}}<{{Q}_{2}}<{{Q}_{3}}
(b) {{Q}_{1}}<{{Q}_{2}}={{Q}_{3}}
(c) {{Q}_{1}}={{Q}_{2}}>{{Q}_{3}}
(d) {{Q}_{1}}>{{Q}_{2}}>{{Q}_{3}}
Ans (a)
2.
An ideal gas at 27°C is compressed adiabatically to 8/27of its original volume. If \gamma =\frac{5}{3}, then the rise in temperature is
(a) 450°C
(b) 375°C
(c) 225°C
(d) 402°C
Ans (d)
3.
One mole of an ideal gas at temperature T was cooled isochorically till the gas pressure fell from P to P/n. Then, by an isobaric process, the gas was restored to the initial temperature. The net amount of heat absorbed by the gas in the process is
(a) nRT
(b) \frac{{RT}}{n}
(c) RT(1-{{n}^{{-1}}})
(d) RT(1-n)
Ans (c)
4.
If one mole of a monatomic gas \left( {\gamma =\frac{5}{3}} \right) is mixed with one mole of a triatomic gas \left( {\gamma =\frac{4}{3}} \right), the value of \gamma for the mixture is
(a) 1.40
(b) 1.44
(c) 1.53
(d) 3.07
Ans(d)
5.
Certain perfect gas is found to obey P{{V}^{{3/2}}}=\mathbf{constant} during an adiabatic process. If such a gas at initial temperature T is adiabatically compressed to half the initial volume, its final temperature will be
(a) \sqrt{2}T
(b) 2T
(c) 2\sqrt{2}T
(d) 4T
Ans (a)
6.
The pressure of the air inside the motor tyre is 2 atmosphere and the temperature is 27°C. If it suddenly bursts, the final temperature will be (\gamma =1.4)
(a) 27 K
(b) –150°C
(c) –81°C
(d) –27°C
Ans(d)
7.
A gas at pressure P is adiabatically compressed so that its density becomes twice that of initial value. Given that the ratio of specific heat at constant pressure and constant volume is 7/5. What will be the final pressure of the gas? ( {{\log }_{{10}}}2=0.3010)
(a) P
(b) 2P
(c) 2.6 P
(d) \frac{{\mathbf{7P}}}{\mathbf{5}}
Ans (c)
8.
If R= universal gas constant then the amount of heat needed to raise the temperature of 2 mol of an ideal monoatomic gas from 273 K to 373K when no work is done, is
(a) 100 R
(b) 150 R
(c) 300 R
(d) 500 R
Ans (c)
Practice Questions (JEE Main Level)
1.
In an adiabatic change
(a) the change takes place slowly and the system is in good thermal contact with the surroundings
(b) the change takes place quickly and the system is in good thermal contact with the surroundings
(c) the change takes place slowly and the system is thermally insulated from the surroundings
(d) the change takes place quickly and the system is thermal insulated form the surroundings
Ans (d)
2.
In an adiabatic change, the pressure P and temperature T of a diatomic gas the related by the relation P\propto {{T}^{C}}, where C equals
(a) 5/3
(b) 2/5
(c) 3/5
(d) 7/2
Ans (d)
3.
In an adiabatic expansion of air the volume increases by 5%. The percentage change in pressure is
(a) 2%
(b) 3%
(c) 5%
(d) 7%
Ans (d)
4.
2 kg of water is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J/kgK and its densities are 999.9 kg/m3 and 1000 kg/m3 respectively at these temperatures. The atmospheric pressure is 105 Pascal. The change in the internal energy is
(a) 33.6 kJ
(b) (33.6+\ 2\ \times \ {{10}^{{-5}}})kJ
(c) (33.6\ +\ {{10}^{5}}\ \times \ 2)\ \mathbf{kJ}
(d) zero
Ans (d)
5.
A gas consisting of diatomic molecules is expanded adiabatically. How many times has the gas to be expanded to reduce the root mean square velocity of molecules to 2/3 of the initial value?
(a) 7.6
(b) 2.8
(c) 5.2
(d) 1.5
Ans (a)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
