Video Lecture
Theory For Notes Making
Buoyancy and archimede’s principle
If an object is immersed in or floating on the surface of, a liquid, it experiences a net vertically upward force due to liquid pressure. This force is called as Buoyant force or force of Buoyancy and it acts from the center of gravity of the displaced liquid. According to Archimede’s principle the magnitude of force of buoyancy is equal to the weight of the displaced liquid.
To prove Archimede’s principle consider a body totally immersed in a liquid as shown in the figure.
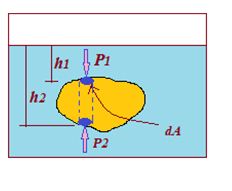
The vertical force on the body due to liquid pressure may be found most easily by considering two small elemental area dA each lying in the same vertical line shown by blue small circular areas.
The net vertical force on the body due to these elements is
dF= (P2 – P2) dA
to get the total net vertical force or upthrust on the whole body we integrate
upthrust = \left[ {\left( {{{P}_{0}}+\,\rho \int{{g{{h}_{2}}}}} \right)-\left( {{{P}_{0}}+\rho \int{{g{{h}_{1}}}}} \right)} \right]Da
upthrust = \rho \,g\int{{\left( {{{h}_{2}}-{{h}_{1}}} \right)}}\text{ }dA
But (h2 – h1) dA= dV, the volume of the part of body formed by the dotted lines as shown in the figure. Thus
Net vertical force on the body F = \rho g\int{{dV}}= V \displaystyle \rho g
here V is the submerged volume of body, in the case considered it is the whole volume of the body. It is also called the volume of displaced liquid. Since [katex] \displaystyle \rho [/katex] is he density of liquid therefore Vx[katex] \displaystyle \rho [/katex]
is the mass of displaced liquid
Force of Buoyancy or upthrust = V \displaystyle \rho g = weight of the displaced liquid
Expression For The Immersed Volume Of Floating Body
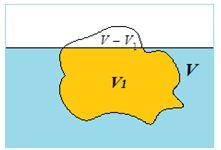
Let a solid of volume V and density p floats in a liquid of density σ with a volume V1 immersed inside the liquid.
The weight of the floating body = V \displaystyle \rho g
The weight of the displaced liquid = V1σg
For the equilibrium of the floating body
V1σg= V \displaystyle \rho g or \frac{{{{V}_{1}}}}{V}\,\,\,\,=\,\,\,\,\frac{\rho }{\sigma } or {{V}_{1}}\,\,\,=\,\,\,\frac{\rho }{\sigma }\,\,\times \,\,V
Immersed volume = \frac{{\text{density of solid}}}{{\text{density of liquid}}}´ volume of solid = \frac{{\text{mass of solid}}}{{\text{density of liquid}}}
From the above relations it is clear that the density of the solid must be less than the density of the liquid to enable it to float freely in the liquid. However a metal vessel may float in water though the density of metal is much higher than that of water. The reason in that the floating bodies are hollow inside and hence they have a large displaced volume. When they float in water the weight of the displaced water is equal to the weight of the body.
Laws of floatation
The principle of Archimedes may be applied to floating bodies to give the laws of floatation as follows:
(i)
When a body floats freely in a liquid the weight of the body is equal to the weight of the liquid displaced.
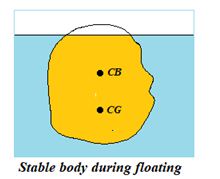
(ii)
The centre of gravity of the displaced liquid (called the centre of buoyancy) lies vertically above or below the centre of gravity of the body. If it lies above the center of gravity the body is said to be in stable equilibrium during floating otherwise the body remains unstable.
Illustration
What fraction of the total volume of an iceberg floating on sea-water is exposed? The density of ice is 920 kg/m3 and that of sea-water is 1030 kg/m3.
Solution:
If V and V1 be the total and submerged volumes of the iceberg
\frac{{{{V}_{1}}}}{V}\,\,=\,\,\frac{{\text{density of iceberg}}}{{\text{density of sea-water}}}\,\,=\,\,\frac{{920}}{{1030}}\,\, =\,\,\frac{{92}}{{103}}
Now the fraction of volume exposed = \frac{{V\,\,-\,\,{{V}_{1}}}}{V}\,\,=\,\,1\,\,\,-\,\,\,\frac{{{{V}_{1}}}}{V} \,\,=\,\,1\,\,\,-\,\,\,\,\frac{{92}}{{103}}\,\,=\,\,\frac{{11}}{{103}} = 10.7%
Illustration
When a boulder of mass 240 kg is placed on a floating iceberg it is found that the iceberg just sinks. What is the mass of the iceberg? Take the relative density of ice as 0.9 and that of sea-water as 1.02.
Solution:
Let M be the weight of iceberg in kg. Then its volume
V\,\,=\,\,\frac{M}{{0.9\,\,\times \,\,{{{10}}^{3}}}}\,\,{{m}^{3}}\,\,=\,\,\frac{M}{{900}}\,\,{{m}^{3}}
When this volume just sinks under sea-water, the weight of water displaced = V´ 1020 kg.
From the principle of buoyancy, this weight must be equal to the weight of iceberg and the boulder on it.
M + 240 = \frac{M}{{900}}´ 1020 = M´ \frac{{102}}{{90}}
or M\ \left( {\frac{{102}}{{90}}\,\,-\,\,1} \right)\,\, = 240
or M\,\,=\,\,\frac{{240\,\,\times \,\,90}}{{12}}= 1800 kg
The mass of the iceberg = 1800 kg
Relative Density
In case of a liquid, sometimes another term relative density (R.D.) is defined. It is the ratio of density of the substance to the density of water at 4°C.
Hence, \text{R}\text{.D}\text{.}=\frac{{\text{Density of substance}}}{{\text{Density of water at 4}{}^\circ \text{C}}}
R.D. is a pure ratio. So, it has no units. It is also sometimes referred as specific gravity.
Density of water at 4°C in CGS is 1gm/cm3. Therefore, numerically the R.D. and density of substance (in CGS) are equal. In SI unit the density of water at 4°C is 1000 kg/m3.
Illustration
Relative density of an oil is 0.8. Find the absolute density of oil in CGS and SI units.
Solution:
Density of oil (in CGS) = (R.D.) gm/cm3
= 0.8 g/cm3
= 800 kg/m3
Illustration
The volume of a body is V and its density is d’. Density of water is d and d’>d. The body is submerged inside water and is lifted through a height h in water. Which of the following is correct?
(a) The potential energy of the body increases by hVdg
(b) P.E. increases by hV(d’–d)g
(c) P.E. increases by hV(d’ + d)g
(d) P.E. decreases
Solution:
The resultant downward force on the sinking particle = Vd‘g – Vdg = V(d’ – d)g. When it is lifted up work is done against this force, W = hV(d’ – d)g = P.E. gained
∴ (b)
Objective Assignment
Q.1
Equal masses of water and a liquid of specific density 2 are mixed together; then mixture has a specific density of:
(a) 2/3 (b) 4/3 (c) 3/2 (d) 3
Ans. (b)
Q.2
A beaker containing water weighs 100 g. It is placed on the pan of a balance and a piece of metal weighing 70 g and having a volume of 10 cm3 is placed inside the water in the beaker. The weight of the beaker and the metal would be:
(a) 170 g (b) 160 g (c) 100 g (d) 30 g
Ans. (a)
Q.3
When a ship floats on water:
(a) It displaces no water
(b) The mass of water displaced is equal to the mass of the ship
(c) The mass of water displaced is lesser than the mass of the ship
(d) The mass of water displaced is greater than the mass of the ship
Ans. (b)
Q.4
A solid is completelyimmersed in a liquid. The force exerted by the liquid on the solid will
(a) increase if it is pushed deeper inside the liquid
(b) change if its orientation is changed keeping it inside
(c) decrease if it is taken partially out of the liquid
(d) be in the horizontal direction only.
Ans. (c)
Q.5
When a piece of ice floating in a beaker of water completely melts, the level of water in the beaker:
(a) Rises
(b) Falls
(c) Remains unchanged
(d) Rises or falls depending upon the quantity of ice and water
Ans. (c)
Q.6
When a cube of wood floats in water, 60% of its volume is submerged. When the same cube floats in an unknown fluid, 85% of its volume is submerged. Find the densities of the wood and the unknown fluid.
(a) rwood = 4 ´ 102 kg/m3, rliquid = 7.37 ´ 102 kg/m3
(b) rwood = 6 ´ 102 kg/m3, rliquid = 6.83 ´ 102 kg/m3
(c) rwood = 6 ´ 102 kg/m3, rliquid = 7.05 ´ 102 kg/m3
(d) rwood = 7.05 ´ 102 kg/m3, rliquid = 6 ´ 102 kg/m3
Ans (c)
comprehension (Q.7 to Q.8)
A block of wood weighs 12 kg and has a relative density 0.6. It is to be in water with 0.9 of its
volume immersed. What weight of a metal is needed[R.D. of metal = 14]
Q.7
if the metal is on the top of wood
(a) 1 kg
(b) 2 kg
(c) 5 kg
(d) 6 kg
Ans (d)
Q.8
if the metal is attached below the wood?
(a) 6.5 kg
(b) 8 kg
(c) 10 kg
(d) 15 kg
Ans (a)
Q.9
A cylindrical solid body of cross-section area 50 cm2 and length 10 cm is floating on mercury with 2.5 cm of its length below the surface. Cross-section area of mercury container is 150 cm2. What is the minimum volume of water required to completely submerge the cylinder in water.
(Specific gravity of water and mercury are 1 and 13.6 respectively).
(a) 800 cm3
(b) 810 cm3
(c) 850 cm3
(d) 900 cm3
Ans(b)
Q.10
A body floats in a liquid contained in a beaker. The whole system as shown in figure falls freely under gravity. The upthrust on the body due to the liquid is:
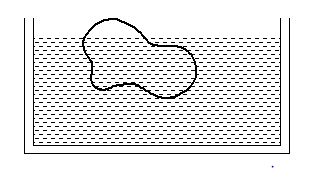
(a) Zero
(b) Equal to the weight of the liquid displaced
(c) Equal to the weight of the body in air
(d) Equal to the weight of the immersed portion of the body
Ans. (a)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
