Video Lecture
Theory For Notes Making
Types of Solids
A solid is that state of matter in which its constituent atoms or molecules are held strongly at the position of minimum potential energy and it has a definite shape and volume. The solids can be classified into two categories, crystalline and glassy or amorphous solids.
Different Properties of Matter
(1) Elasticity :
The property of matter by virtue of which a body tends to regain its original shape and size after the removal of deforming force is called elasticity.
(2) Plasticity :
The property of matter by virtue of which it does not regain its original shape and size after the removal of deforming force is called plasticity.
(3) Elastic limit :
Elastic bodies show their property of elasticity upto a certain value of deforming force. If we go on increasing the deforming force then a stage is reached when on removing the force, the body will not return to its original state. The maximum deforming force upto which a body retains its property of elasticity is called elastic limit of the material of body.
Elastic limit is the property of a body whereas elasticity is the property of material of the body.
Stress
When a force is applied on a body, there will be relative displacement of the particles and due to property of elasticity, an internal restoring force is developed which tends to restore the body to its original state.
The internal restoring force acting per unit area of cross section of the deformed body is called stress.
If external force F is applied on the area A of a body then,
Stress =\frac{{\text{Force }}}{{\text{Area}}}=\frac{F}{A}
Unit : N/{{m}^{2}} (S.I.) , dyne/c{{m}^{2}} (C.G.S.)
Dimension : [M{{L}^{{-1}}}{{T}^{{-2}}}]
Stress developed in a body depends upon how the external forces are applied over it.
On this basis there are different types of stresses :
(i) Longitudinal Stress
(ii) Volumetric Stress
(iii) Shear or tangential stress
(i)
Longitudinal stress
(a) It occurs only in solids and comes in to picture when deforming force is applied parallel to the length and causes increase in length as shown in the figure.
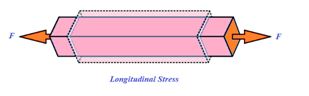
In this case the restoring force induced per unit area is called longitudinal stress. The area taken for calculation of stress is the area of cross section. Longitudinal stress produced due to increase in length of a body under a deforming force is called tensile stress. Whereas the Longitudinal stress produced due to decrease in length of a body under a deforming force is called compressive stress.
Volumetric Stress
This type of stress is produced when deforming force is applied normally to the surface at all points as shown in the figure.
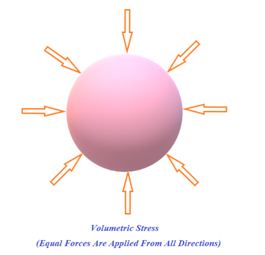
In such situations the restoring force induced per unit area is called Volumetric stress or Hydrostatic stress. It occurs in solids, liquids and gases. This stress produces change in volume and density, shape remaining same. For calculation of this stress the complete surface area perpendicular to the applied forces is used. It is equal to change in pressure because change in pressure is responsible for change in volume.
Shear or tangential stress :
It comes into picture when successive layers of solid move on each other i.e. when there is a relative displacement between various layers of solid. Here deforming force is applied tangential to the faces as shown in the figure
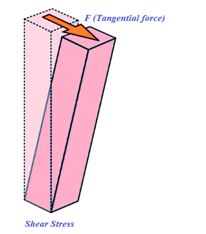
To calculate this stress the area of the face on which force is applied is taken into consideration.
Strain
The ratio of change in configuration to the original configuration is called strain.
Being the ratio of two like quantities, it has no dimensions and units.
Strain are of three types :
Linear or Longitudinal strain :
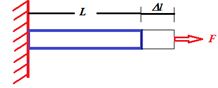
If the deforming force produces a change in length alone, the strain produced in the body is called linear strain or longitudinal strain.
\text{Linear strain}=\frac{{\text{Change in length(}\Delta l\text{)}}}{{\text{Original length(}l\text{)}}}
Linear strain in the direction of deforming force is called longitudinal strain and in a direction perpendicular to force is called lateral strain.
Volumetric strain :
If the deforming force produces a change in volume alone the strain produced in the body is called volumetric strain.
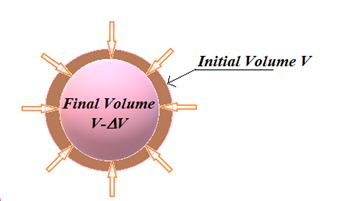
\text{Volumetric strain}=\frac{{\text{Change in volume(}\Delta V\text{)}}}{{\text{Original volume(}V\text{)}}}
Shearing strain :
If the deforming force produces a change in the shape of the body without changing its volume, strain produced is called shearing strain.
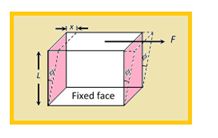
It is defined as angle in radians through which a plane perpendicular to the fixed surface of the cubical body gets turned under the effect of tangential force.
\varphi =\frac{x}{L}
Hooke’s law and moduli of elasticity
According to Hooke’s law, “within elastic limit stress is proportional to strain”
i.e. \frac{{\text{stress}}}{{\text{strain}}}= constant = λ
where λ is called modulus of elasticity. Depending upon different types of strain the following three moduli of elasticity are possible.
(i) Young’s modulus:
When a wire or rod is stretched by a longitudinal force, the ratio of the longitudinal stress to the longitudinal strain within the elastic limits is called Young’s modulus.
Young’s modulus (Y) = \frac{{\text{Longitudinal}\ \ \text{stress}}}{{\text{Linear}\ \ \text{strain}}}
Consider a wire or rod of length L and radius r under the action of a stretching force F applied normal to its faces. Suppose the wire suffers a change in length l then
Longitudinal stress = \frac{F}{{\pi {{r}^{2}}}}
Linear strain = \frac{l}{L}
Young’s modulus (Y) = \frac{{\frac{F}{{\pi {{r}^{2}}}}}}{{\frac{l}{L}}}= \frac{{FL}}{{\pi {{r}^{2}}l}}
(ii) Bulk modulus:
When a solid or fluid (liquid or gas) is subjected to a uniform pressure all over the surface, the shape remains the same, but there is a change in the volume. The force per unit area applied normally and uniformly over the surface is called normal stress. The change in volume per unit volume is called volume or bulk strain. The ratio \frac{{\text{Volume}\ \,\text{stress}\,\,\ \text{or}\,\,\ \text{normal}\,\,\,\ \text{stress}}}{{\text{Volume}\,\,\,\text{strain}}} is called bulk modulus (B).
In symbol B = – \frac{F}{{\frac{A}{{\frac{{\Delta V}}{V}}}\,}}\,=\,\,-\,\frac{{FV}}{{A\Delta V}}=-\frac{P}{{\Delta V/V}}
The reciprocal of bulk modulus is called compressibility (K).
Compressibility (K) = \frac{1}{{\text{bulk}\ \,\,\text{modulus}}}
Density of Compressed Liquid
If a liquid of density \rho , volume V and bulk modulus K is compressed, then its density increases.
As density \rho =\frac{m}{V} so \frac{{\Delta \rho }}{\rho }=\frac{{-\Delta V}}{V} …(i)
But by definition of bulk modulus
K=\frac{{-V\Delta P}}{{\Delta V}} ⇒ -\frac{{\Delta V}}{V}=\frac{{\Delta P}}{K} …(ii)
From (i) and (ii) \frac{{\Delta \rho }}{\rho }= \frac{{{\rho }’-\rho }}{\rho }=\frac{{\Delta P}}{K} [As Dr = r’ – r ]
or {\rho }’=\rho \left[ {1+\frac{{\Delta P}}{K}} \right] =\rho [1+C\Delta P] \left[ {\text{As }\frac{\text{1}}{K}=C} \right]
(iii) Modulus of Rigidity:
According to definition, the ratio of shearing stress to shearing strain is called modulus of rigidity (h). In this case the shape of the body changes but its volume remains unchanged. Consider the case of a cube fixed at its lower face and acted upon by a tangential force F on its upper surface of area A as shown in figure.
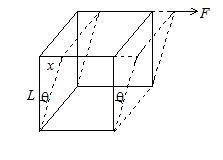
shearing stress = \frac{F}{A}
shearing strain = θ = \left( {\frac{x}{L}} \right)
η = \frac{F}{{A\theta }}
Elastic energy stored in a deformed body
The elastic energy is measured in terms of work done in straining the body up to its
elastic limit.
Let F be the force applied across the cross-section A of a wire of length L. Let l be the increase in length. Then
Y = \frac{{\ \ \frac{F}{A}\ \ }}{{\frac{l}{L}}}\ =\ \frac{{FL}}{{A\ \ l}} or F = \frac{{Y\ A\ \ l}}{L}
If the wire is stretched through a further distance (d l) the work done = F´ (dl) = \frac{{Y\ A\ \ l}}{L}\ \,\ (dl)
Total work done in stretching the wire from original length L to a length (L + l)
(i.e. from l = 0 to l = l)
W = \int\limits_{0}^{l}{{\frac{{Y\ A\ \cdot \ l}}{L}\ \cdot \ dl}} = \frac{{YA}}{L}\ \cdot \ \frac{{{{l}^{2}}}}{2}\ \ =\ \ \frac{1}{2}\ \ (AL)\ \ \left( {\frac{{Yl}}{L}} \right)\ \ \left( {\frac{l}{L}} \right)
W = 1/2´ volume ´ stress ´ strain
\frac{{\text{Workdone}}}{{\text{Volume}}}=\frac{1}{2}\times \text{stress strain}=\text{Elastic energy}.
Stress-strain Curve
If a curve is plotted on the graph between stress (or load) and longitudinal strain (or elongation) by gradually increasing the load on a vertically suspended metal wire, we get the curve as shown in figure. This curve is called stress – strain curve.
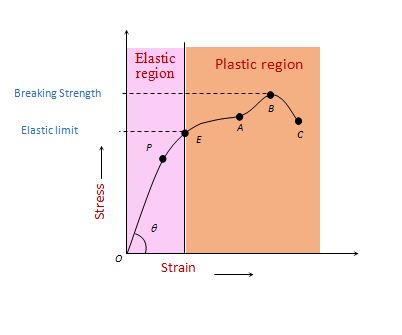
From this curve following observations can be drawn.
(1)
For small strain (< 2%) (i.e., in region OP) stress is proportional to strain. This is the region where Hooke’s law is obeyed. The point P is called elastic limit and slope of line OP gives the Young’s modulus Y of the material of the wire. If θ is the angle of OP from strain axis then young’s modulus Y = tanθ.
(2)
If the strain is increased a little bit, i.e., in the region PE, the stress is not proportional to strain. However, the wire still regains its original length after the removal of stretching force. This behavior is shown up to point E known as yield-point. The region OPE represents the elastic region of the material of wire.
(3)
If the wire is stretched beyond point E, i.e., between EA, the strain increases much more rapidly and if the stretching force is removed the wire does not come back to its natural length. Some permanent increase in length takes place.
(4)
If the stress is increased further, by a very small increase in it a very large increase in strain is produced (region AB) and after reaching point B, the strain increases even if the wire is unloaded and ruptures at C. The maximum stress corresponding to B after which the wire begins to flow and breaks is called breaking or ultimate tensile strength. The region EABC represents the plastic behavior of the material of wire.
Elastic Hysteresis
When a deforming force is applied on a body then the strain does not change simultaneously with stress rather it lags behind the stress. The lagging of strain behind the stress is defined as elastic hysteresis. This is the reason why the values of strain for same stress are different while increasing the load and while decreasing the load.
Hysteresis loop :
The area of the stress-strain curve is called the hysteresis loop and it is numerically equal to the work done in loading the material and then unloading it.
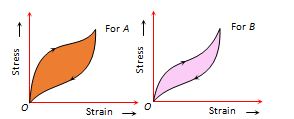
If we have two tyres of rubber having different hysteresis loop then rubber B should be used for making the car tyres. It is because of the reason that area under the curve i.e. work done in case of rubber B is lesser and hence the car tyre will not get excessively heated and rubber A should be used to absorb vibration of the machinery because of the large area of the curve, a large amount of vibrational energy can be dissipated.
Factors Affecting Elasticity
(1)
Hammering and rolling :Crystal grains break up into smaller units by hammering and rolling. This results in increase in the elasticity of material.
(2)
Annealing : The metals are annealed by heating and then cooling them slowly. Annealing results in decrease in the elasticity of material.
(3)
Temperature : Intermolecular forces decreases with rise in temperature. Hence the elasticity decreases with rise in temperature but the elasticity of invar steel (alloy) does not change with change of temperature.
(4)
Impurities : Due to impurities in a material, elasticity can increase or decrease. The type of effect depends upon the nature of impurities present in the material.
Poisson’s ratio:
When a longitudinal force is applied on a wire, its length increases but its radius decreases. Thus two strains are produced by a single force:
(i) Longitudinal strain =\frac{{\Delta l}}{l} and
(ii) Lateral strain =\frac{{\Delta R}}{R}
The ratio of these two strains is called the Poisson’s ratio.
Thus, the Poisson’s ratio \text{ }\!\!\sigma\!\!\text{ }=\frac{{\text{(–) Lateral}\,\text{strain}}}{{\text{Longitudinal}\ \text{strain}}}
Following points are important in case of Poisson’s ratio:
(i) Negative sign in s indicates that radius of the wire decreases as the length increases.
(ii) Theoretical value of s lies between –1 and +\frac{1}{2}.
(iii) Practical value of s lies between 0 and +\frac{1}{2}.
8 Relation between Y (Young’s Modulus), B(Bulk Modulus), h(Modulus of rigidity) and s(Poisson’s ratio):
Following are some relations between the four
(a) B=\frac{Y}{{3(1-2\sigma )}}
(b) \eta =\frac{Y}{{2(1+\sigma )}}
(c) \sigma =\frac{{3B-2\eta }}{{2\eta +6B}}
(d) \frac{9}{Y}=\frac{1}{B}+\frac{3}{\eta }.
Illustration
A rectangular bar having a cross-sectional area of 70 mm2 has a tensile force of 14 kN applied to it. Determine the stress in the bar.
Solution:
Cross-sectional area A = 70 mm2= 70 × (10–3)2 m2 = 70 x 10–6 m2
Tensile force F = 14 kN = 14 x 103 N
Stress in the bar = \frac{{\text{Force}}}{{\text{Area}}}\ \ =\ \ \frac{{14\ \,\times \,\ {{{10}}^{3}}\ \text{N}}}{{70\ \,\times \,\ {{{10}}^{{-6}}}\ {{\text{m}}^{2}}}}= 0.20 x 109 N/m2
= 2 × 108 N/m2 = 2 × 108 Pa
(Q 1Pa = 1N/m2 )
Illustration
A wire of length 2.5 m has a percentage strain of 0.012% under a tensile force. Determine the extension in the wire.
Solution:
Original length of wire L = 2.5 m
Longitudinal Strain = 0.012 % = \frac{{0.012}}{{100}}
Strain = \frac{{\text{Extension}\ \ \text{in}\ \ \text{length}}}{{\text{Original}\ \ \text{length}}}\ =\ \frac{{\Delta L}}{L}
\frac{{\Delta L}}{L} = \frac{{0.012}}{{100}}
DL = \frac{{0.012}}{{100}}\ \,\times \,\ L\,\ =\,\ \frac{{0.012}}{{100}}\ \,\times \,\ 2.5 = 0.3 x 10-3 m
Extension = 3 x 10–4 m. Ans.
Illustration
A wire is stretched by 2 mm when a force of 250 N is applied. Determine the force that would stretch the wire by 5 mm assuming that the elastic limit is not exceeded.
Solution:
According to Hooke’s law, within elastic limits, xµF
or x = kF where k is a constant.
It is given that when x = 2 mm, F = 250 N
\frac{2}{{250}}=\frac{S}{F}
or the force required F = \frac{5}{2}\ \,\,\times \ \,\,250 = 625 N
Illustration
The rubber cord of catapult has a cross-sectional area 1 mm2 and total unstretched length 10 cm. It is stretched to 12 cm and then released to project a body of mass 5 gm. Taking the Young’s modulus of rubber as 5 ´ 108 N/m2, calculate the velocity of projection.
Solution:
It can be assumed that the total elastic energy of catapult is converted into kinetic energy of body without any heat loss.
Elastic energy = 1/2 x load x extension
Extension = 12 – 10 = 2 cm = 2 x 10–2m
Y = \frac{{FL}}{{A\Delta L}}
F = \frac{{5\ \,\times \,\ {{{10}}^{8}}\,\ \times \,\ 1\,\ \times \,\ {{{10}}^{{-6}}}\ \,\times \,\ 2\ \,\times \ \,{{{10}}^{{-2}}}}}{{10\ \,\times \ \,{{{10}}^{{-2}}}}} = 100 N
If v is the velocity of projection,
Elastic energy of catapult = Kinetic energy of missile
½ x load x extension = \frac{1}{2}m{{v}^{2}}
\frac{1}{2}\ \,\times \ \,100\ \,\times \ \,2\ \,\times \ \,{{10}^{{-2}}} = \frac{1}{2}\ \,\times \ \,5\ \,\times \ \,{{10}^{{-3}}}\ \times \ \,{{v}^{2}}
v2 = \frac{{100\ \,\times \ \,{{{10}}^{{-2}}}\ \times \ \,2}}{{5\,\ \times \,\ {{{10}}^{{-3}}}}} = 400
v = 20 m/s
Illustration
Two steel wires of length 1 m and 2 m have diameters 1 mm and 2 mm respectively. If they are stretched by forces of 40 N and 80 N respectively their elongation will be in the ratio of
(1) 1 : 1
(2) 2 : 1
(3) 4 : 1
(4) 1 : 8
Solution:
Young’s modulus: Y\ \,=\,\ \frac{{{{F}_{1}}/{{A}_{1}}}}{{\Delta {{L}_{1}}/{{L}_{1}}}}\ \,=\ \,\frac{{{{F}_{2}}/{{A}_{2}}}}{{\Delta {{L}_{2}}/{{L}_{2}}}}
\ \frac{{\Delta {{L}_{1}}}}{{\Delta {{L}_{2}}}}\ \,=\ \,\frac{{{{F}_{1}}{{L}_{1}}}}{{{{F}_{2}}{{L}_{2}}}}\ \,\times \ \,\frac{{{{A}_{2}}}}{{{{A}_{1}}}} =\ \,\frac{{40\ \,\times \,\ 1}}{{80\,\ \times \ \,2}}\ \,\times \ \,\frac{{{{2}^{2}}}}{{{{1}^{2}}}}\ \,=\ \,\text{1}
(1)
Illustration
The following four wires are made of the same material. Which of these will have the largest extension when the same tension is applied to all?
(1) L = 50cm;D=0.05mm
(2) L = 100 cm; D = 1 mm
(3) L = 200 cm; D = 2 mm
(4) L = 300 cm; D = 3 mm
Solution:
Extension: \Delta L\,\ =\,\ \frac{{FL}}{{AY}}\ \,\propto \ \,\frac{L}{A} (QF and Y are common)
\frac{L}{A} is maximum in case of (1)
(1)
Illustration
A wire of length L, radius r, when stretched with a force F, changes in length by l. What will be the change in length in a wire of same material having length 2L, radius 2r and stretched by a force 2F?
(1) \frac{l}{2}
(2) l
(3) 2 l
(4) 4L
Solution:
Y = \frac{{\frac{F}{A}}}{{\left( {\frac{{\Delta \ell }}{\ell }} \right)}}\,\,\,\ \Rightarrow \ \,\frac{{\left( {\frac{F}{{\pi {{r}^{2}}}}} \right)}}{{\left( {\frac{\ell }{L}} \right)}}\ \,\,=\ \,\,\frac{{\left( {\frac{{2F}}{{4\ \pi {{r}^{2}}}}} \right)}}{{\left( {\frac{{\Delta \ell }}{{2L}}} \right)}}
\frac{1}{l}\ =\ \frac{1}{{\Delta l}}
Δl = l
(2)
Objective Assignment
Q.1
Which of the following substance has the highest elasticity
(a) steel (b) copper (c) rubber (d) sponge
Ans. (a)
Q.2
An elastic metal rod will not change its length when it
(a) falls vertically under its weight
(b) is pulled along its length by a force acting at one end
(c) rotates about an axis at one end
(d) slides on a rough surface
Ans. (a)
Q.3
Which of the following substances has the highest value of the Young’s modulus:
(a) Steel (b) Rubber (c) Wood (d) Plastic
Ans. (a)
Q.4
Energy stored per unit volume in a stretched wire is:
(a) ½ Load ´ Strain
(b) Load ´ Strain
(b) Stress ´ Strain
(d) ½ Stress ´ Strain
Ans. (d)
Q.5
The following four wires are made of the same material. Which of these will have the largest extension when the same tension is applied:
(a) Length = 50 cm and diameter = 0.5 mm
(b) Length = 100 cm and diameter = 1 mm
(c) Length = 200 cm and diameter = 2 mm
(d) Length = 300 cm and diameter = 3 mm
Ans. (a)
Q.6
A wire (Y = 2 ´ 1011 N/m2) has length 1 m and area of cross-section 1 mm2; the work required to increase its length by 2 mm is:
(a) 0.4 kJ (b) 40 kJ (c) 4 kJ (d) 400 kJ
Ans. (d)
Q.7
A metal wire of length L, area of cross-section A and Young modulus Y is stretched by a variable force F, such that F is always slightly greater than elastic force of resistance in the wire. If the elongation of the wire is l, then which of the following is incorrect.
(a) the work done by F is \frac{{YA{{l}^{\text{2}}}}}{{2L}}
(b) the work done by F is \frac{{YA{{l}^{\text{2}}}}}{L}
(c) the elastic potential energy stored in the wire is \frac{{YA{{l}^{\text{2}}}}}{{2L}}
(d) no heat is produced during the elongation
Ans. (b)
Q.8
A metal wire of length L, area of cross-section A and Young modulus Y behaves as a spring of spring constant k.
(a) k = YA/L (b) k = 2YA/L (c) K = YA/2L (d) K = YL/A
Ans. (a)
Q.9
A uniform rod of mass m, length L, area of cross-section A and Young modulus Y hangs from the ceiling. Its elongation under its own weight will be
(a) zero
(b) \frac{{mgL}}{{2AY}}
(c) \frac{{mgL}}{{AY}}
(d) \frac{{2mgL}}{{AY}}
Ans. (b)
comprehension (Q.10 to Q.12)
A structural steel rod has a radius of 10 mm and a length of 1 m. A 100 kN force stretches it along its length. Calculate
Given that the Young’s modulus of elasticity of the structural steel is 2.0 ´ 1011 N/m2.
Q.10
the stress
(a) 3.18 ´ 108 N/m2
(b) 5.36 ´ 108 N/m2
(c) 0.83 ´ 108 N/m2
(d) 9.27 ´ 108 N/m2
Ans (a)
Q.11
elongation and
(a) 0.35 mm
(b) 1.59 mm
(c) 3.43 mm
(d) 7.28 mm
Ans (b)
Q.12
percentage strain on the rod.
(a) 1.568%
(b) 0.355%
(c) 1.456%
(d) 0.159%
Ans (d)
Q.13
Compute the bulk modulus of water from the following data:
Initial volume = 100 litre, pressure increase = 100 atmosphere;
Final volume = 100.5 litre. (1 atmosphere = 1.013 ´ 105 Pa).
(a) 1.856 ´ 109 Pa
(b) 0.386 ´ 109 Pa
(c) 2.026 ´ 109 Pa
(d) 2.46 ´ 109 Pa
Ans (c)
comprehension (Q.13 to Q.14)
Calculate the elongations of
Q.13
a copper wire of 1.4 mm diameter and
(a) 0.5 ´ 10-3 m
(b) 0.1 ´ 10-3 m
(c) 0.2 ´ 10-3 m
(d) 1.7 ´ 10-3 m
Ans (d)
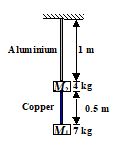
Q.14
analuminium wire of 1 mm diameter as shown in figure.
Young’s modulus of copper and aluminium are
11 ´ 1010 N/m2 and 7 ´ 1010 N/m2 respectively.
(a) 0.36 ´ 10-3 m
(b) 1.96 ´ 10-3 m
(c) 5.74 ´ 10-3 m
(d) 2.45 ´ 10-3 m
Ans (b)
Q.15
The edges of an aluminum cube are 10 cm long. One face of the cube is firmly fixed to a vertical wall. A mass of 100 kg is then attached to the opposite face of the cube. The shear modulus of aluminum is 25 G Pa. What is the vertical deflection of this face?
(g = 10 m/s2, 1 Pa = 1 N/m2).
(a) 0.6 ´ 10-7 m
(b) 4 ´ 10-7 m
(c) 7.5 ´ 10-7 m
(d) 1.764 ´ 10-7 m
Ans (b)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
