Video Lecture
Theory For Making Notes
Newton’s Law of universal Gravitation
Statement: The force of attractions between any two particles varies directly as the product of their masses and inversely proportional to the square of the distance between them.
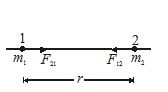
If m1 and m2 be two point masses (particles) and r the distance between them, then the magnitude of the force is
F=G\frac{{{{m}_{1}}{{m}_{2}}}}{{{{r}^{2}}}} …(1)
Where G is a universal constant having the same value for all pairs of particles. In fact there are two forces: one is the force exerted by the first particle on the second particle (F12) towards the first particle along the line joining the two. Likewise, the second particle exerts a force on the first (F21) that is direction towards the second particle along the line joining the two. Thus proper vectorial representation of the gravitational forces are
{{\overrightarrow{F}}_{{12}}}=-G\frac{{{{m}_{1}}{{m}_{2}}}}{{r_{{12}}^{2}}}.\,{{\hat{r}}_{{11}}} …(2)
and {{\overrightarrow{F}}_{{21}}}=-G\frac{{{{m}_{1}}{{m}_{2}}}}{{r_{{21}}^{2}}}.\,{{\hat{r}}_{{21}}}. …(3)
The constant G is 6.67 × 10–11 Nm2Kg–2 in SI.
Definition of G:
Put {{m}_{1}}={{m}_{2}}=1\,\text{kg} are r = 1 m in equation (1).Then F = G. Thus G may be defined as the force between two point masses, each of 1 kg when placed at a distance 1 m from each other.It has the dimensional formulae M–1L3T–2 .
1.1 Experimental evidence in support of Newton’s law of gravitation
1.
It is due to the gravitational force of attraction between the Moon and the sea-water that tides are formed in oceans.
2.
The rotation of Earth around the Sun.
3.
The rotation of Moon around the Earth.
4.
The times of lunar and Solar eclipse calculated on the basis of Newton’s Law of Gravitation, have been found to be approximately correct.
1.2 Salient features of gravitational force
1.
It is always attractive
2.
It is independent of the medium between the particles.
3.
It is always along the line joining the centre of masses in case of two bodies.
4.
It is a conservative force.
Example-1:
A mass M is split into two parts m and (M – m), which are then separated by a certain distance. What ratio (m/M) maximizes the gravitational force between the parts?
Solution: If r is the distance between m and (M – m), the gravitational force will be
F=G\frac{{m(M-m)}}{{{{r}^{2}}}}=\frac{G}{{{{r}^{2}}}}(mM-{{m}^{2}})
For F to be maximum dF/dm = 0 as M and r are constants.
\frac{d}{{dm}}\left[ {\frac{G}{{{{r}^{2}}}}(mM-{{m}^{2}})} \right]=0,
∴ M-2m=0.
or, (m/M)=(1/2),i.e., the force will be maximum when the two parts are equal.
Example-2:
Calculate the gravitational force of attraction between uniform sphere of mass M and a uniform rod of length l and mass m as oriented.
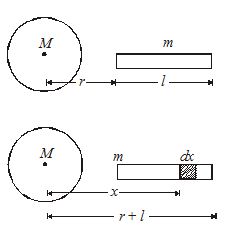
Solution: Mass per unit length =\frac{m}{l}
Mass of section of length dx=\frac{m}{l}dx
Let dF be the gravitational force of attraction between this section and sphere.
Then, dF=GM\frac{{\left( {\frac{m}{l}dx} \right)}}{{{{x}^{2}}}}
F=\int\limits_{r}^{{r+l}}{{\ \ \frac{{GMm}}{{l{{x}^{2}}}}}}dx=\frac{{GMm}}{l}\int\limits_{r}^{{r+l}}{{\ \,\frac{1}{{{{x}^{2}}}}}}dx =\frac{{GMm}}{l}\int\limits_{r}^{{r+1}}{{\ {{x}^{{-2}}}}}dx=\frac{{GMm}}{l}\left[ {\frac{{{{x}^{{-2+1}}}}}{{-2+1}}} \right]_{r}^{{r+l}} =\frac{{GMm}}{{r(r+l)}}
If r>>l, then F=\frac{{GMm}}{{{{r}^{2}}}}.
Example-3:
Two particles of equal mass move in a circle of radius r under the action of their mutual gravitational attraction. Find the speed of each particle if its mass is m.
Solution: The particles will always remain diametrically opposite so that the force on each particle will be directed along the radius. Considering the circulation the circulation of one particle we have
\frac{{m{{v}^{2}}}}{r}=\frac{{Gmm}}{{{{{(2r)}}^{2}}}},i.e., v=\sqrt{{\frac{{GM}}{{4r}}}}.
GRAVITATIONAL FIELD
Gravitational field due to a mass is defined as the region of space in which it interacts with other masses. In order to get the extent of interaction between two masses we defined another quantity called gravitational field intensity. Gravitational field intensity due to a mass m at a distance r is defined as the force acting on unit mass kept at a distance r. The gravitational field intensity is a vector quantity and its direction is the direction along which the unit mass has a tendency to move. The unit of gravitational field intensity is N/kg and its dimensions are [LT-2].
Calculation of gravitational field
(a) Gravitational field intensity due to a point mass
Consider a point mass M at O and let us calculate gravitational intensity at A due to this point mass.
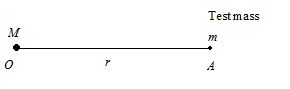
Suppose a test mass is placed at A.
By Newton’s law of gravitation, force on test mass
F = \frac{{GMm}}{{{{r}^{2}}}} along \overset{\to }{\mathop{{AO}}}\,
\vec{E}= \frac{{\vec{F}}}{m} =-\frac{{GM}}{{{{r}^{2}}}} {{\hat{e}}_{r}}
(b) Gravitational field due to a uniform solid sphere
Case I: Field at an external point
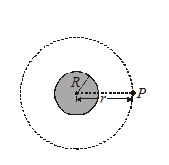
Let the mass of sphere is M and its radius is R, we have to calculate the gravitational field at P.
\int{{dE\,=\,\int{{\frac{{Gdm}}{{{{r}^{2}}}}}}}}= \frac{G}{{{{r}^{2}}}}\,\int{{dm}}\,=\,\frac{{GM}}{{{{r}^{2}}}}
Thus, a uniform sphere may be treated as a single particle of equal mass placed at its centre for calculating the gravitational field at an external point.
Case II: Field at an internal point
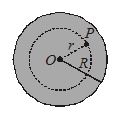
Suppose the point P, is inside the solid sphere, in this case r<R the sphere may be divided into two spherical parts. One of radius r and other beyond that upto radius R.The field at point P is due to sphere of radius r. Now suppose that the mass of such a shell is m. Then
E=\,\frac{{Gm}}{{{{r}^{2}}}}\,\,along PO here m = density x volume of sphere of radius r
hence \displaystyle m=\left( {\frac{M}{{\frac{4}{3}\pi {{R}^{3}}}}} \right)\,\frac{4}{3}\pi {{r}^{3}}\,=\,\frac{{M{{r}^{3}}}}{{{{R}^{3}}}}
∴ E = \frac{{GM}}{{{{R}^{3}}}}\,r
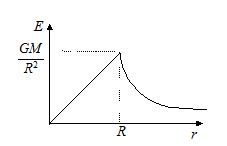
Therefore gravitational field due to a uniform sphere at an internal point is proportional to the distance of the point from the centre of the sphere. At the centre r = 0 the field is zero. At the surface of the sphere r = R
E\,=\,\frac{{GM}}{{{{R}^{2}}}}
(c) Field due to uniform thin spherical shell
Case I: When point lies inside the spherical shell
\int{{dE\,=\,\frac{G}{{{{r}^{2}}}}\,\int{{}}}}dm(enclosed) = 0
Case II: When point P lies outside the spherical shell
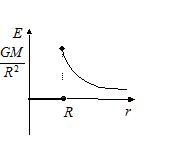
\int{{dE\,=\,\frac{G}{{{{r}^{2}}}}\,\int{{dm\,=\,\frac{{GM}}{{{{r}^{2}}}}}}}}
Illustration 5.
Two thin concentric shells of masses M1 and M2 are present. Calculate the gravitational force on ‘m’ due to M1 and M2when placed at points P, Q and R .
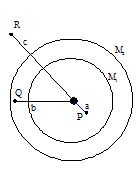
Solution: Field at P, EP = 0 ⇒ F = 0
Field at Q, due to M2 will be zero but there will be field due to M1, EQ = \displaystyle \frac{{G{{M}_{1}}}}{{{{b}^{2}}}}
F = \displaystyle \frac{{G{{M}_{1}}m}}{{{{b}^{2}}}}
Field at R, is the sum of fields due to M1 and M2, ER = \displaystyle \frac{{G({{M}_{1}}+{{M}_{2}})}}{{{{c}^{2}}}}
FR = \displaystyle \frac{{G({{M}_{1}}+{{M}_{2}}).m}}{{{{c}^{2}}}}
Illustration 6.
A spherical shell is cut into two pieces along a chord as shown in figure. For points P and Q [I = magnitude of gravitational field intensity]
(A) IP> IQ
(B) IP< IQ
(C) IP = IQ = 0
(D) IP = IQ≠ 0
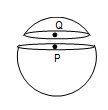
Solution:
(D) At the point P we have Ip – IQ = 0
Because the gravitational field inside a shell cancel due to two pieces shown,
hence Ip =IQ ≠ 0
The gravitational field of a ring on its axis
Let us consider a ring of mass M in the plane perpendicular to the plane of the paper. We want to find the gravitational field on its axis at a distance x.
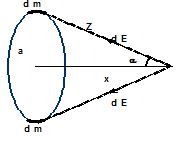
Consider a differential length of the ring of mass dm.
dE = \displaystyle \frac{{Gdm}}{{{{Z}^{2}}}}
The Y components of the fields due to diametrically opposite elements cancel each other. Thus, the X components add up.
\displaystyle E=\int{{\frac{{Gdm}}{{{{z}^{2}}}}\cos \alpha =\frac{{GM\cos \alpha }}{{{{z}^{2}}}}=\frac{{GM.x}}{{{{{({{a}^{2}}+{{x}^{2}})}}^{{3/2}}}}}}}
Field due to a uniform thin spherical shell
Consider a thin spherical shell of radius a, mass M and of negligible thickness. Out of the spherical shell, we consider an element ring on the shell of thickness a dq. The shaded ring has mass dm = (M/2) sin Θ dΘ.
Consider a point P on the axis of the ring.
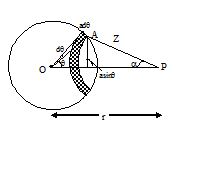
The field at P due to this ring is
\displaystyle dE=\frac{{G.dm}}{{{{z}^{2}}}}\cos \alpha =\frac{{GM}}{2}\frac{{\sin \theta \,d\theta .\cos \alpha }}{{{{z}^{2}}}}
From DOAP,
z2 = a2 + r2– 2ar cos q
or 2zdz = 2ar sin q dq
or sin θ dθ = zdz/a.r
Also, from DOAP,
a2 = z2 + r2– 2zr. cos a
\displaystyle \cos \alpha =\frac{{{{z}^{2}}+{{r}^{2}}-{{a}^{2}}}}{{2.z.r}}
Thus \displaystyle dE=\frac{{GM}}{{4a{{r}^{2}}}}\left[ {1-\frac{{{{a}^{2}}-{{r}^{2}}}}{{{{z}^{2}}}}} \right]dz
\displaystyle or\int{{dE=\frac{{GM}}{{4a{{r}^{2}}}}\left[ {z+\frac{{{{a}^{2}}-{{r}^{2}}}}{z}} \right]}}
Case I: \displaystyle \text{(P is outside the shell, r a)}
\displaystyle E=\frac{{GM}}{{4a{{r}^{2}}}}\left[ {z+\frac{{{{a}^{2}}-{{r}^{2}}}}{z}} \right]_{{r-a}}^{{r+a}}=\frac{{GM}}{{{{r}^{2}}}}
We see that the uniform shell may be treated as a point particle of the same mass placed at its centre to calculate the gravitational field at an external point.
Case II (Inside the shell, r < a).
\displaystyle E=\frac{{GM}}{{4a{{r}^{2}}}}\left[ {z+\frac{{{{a}^{2}}-{{r}^{2}}}}{z}} \right]_{{a-r}}^{{a+r}}=0
We see that the field inside a uniform spherical shell is zero.
Practice Questions (Basic Level)
1.
A mass M is split into two parts m and (M – m), which are then separated by a certain distance. What ratio (m/M) maximises the gravitational force between the parts.
(a) 1/2
(b) 1/4
(c) 1/8
(d) 1/3
Ans (a)
2.
The force between a hollow sphere and a point mass at P inside it as shown in fig.
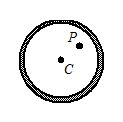
(a) is attractive and constant
(b) is attractive and depends on the position of the point with respect to centre C
(c) is zero
(d) is repulsive and constant
Ans (c)
3.
The tidal waves on the sea are primarily due to
(a) Gravitational effect of the moon on the earth
(b) Gravitational effect of the sun on the earth
(c) Gravitational effect of the sun and moon on the earth.
(d) Gravitational effect of the earth on the sun
Ans (a)
Comprehension Based Question (4 and 5)
The magnitudes of gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are I1 and I2 respectively. Find the ratio of (I1/I2) if
4.
r1>R and r2>R
(a) \frac{{{{I}_{1}}}}{{{{I}_{2}}}}=\frac{{r_{2}^{3}}}{{r_{1}^{3}}}
(b) \frac{{{{I}_{2}}}}{{{{I}_{2}}}}=\frac{{r_{2}^{2}}}{{r_{1}^{2}}}
(c) \frac{{{{I}_{1}}}}{{{{I}_{2}}}}=\frac{{r_{2}^{2}}}{{r_{1}^{2}}}
(d) \frac{{{{I}_{1}}}}{{{{I}_{2}}}}=\frac{{r_{2}^{1}}}{{r_{1}^{2}}}
Ans (c)
5.
r1<R and r2<R.
(a) \frac{{{{I}_{1}}}}{{{{I}_{2}}}}=\frac{{{{r}_{1}}}}{{{{r}_{2}}}}
(b) \frac{{{{I}_{1}}}}{{{{I}_{1}}}}=\frac{{{{r}_{1}}}}{{{{r}_{2}}}}
(c) \frac{{{{I}_{2}}}}{{{{I}_{2}}}}=\frac{{{{r}_{2}}}}{{{{r}_{2}}}}
(d) \frac{{{{I}_{2}}}}{{{{I}_{2}}}}=\frac{{{{r}_{2}}}}{{{{r}_{2}}}}
Ans (a)
6.
If a body of mass m be projected vertically upward from the surface of the earth so as to reach a height nR above the earth’s surface. Calculate the increase in its P.E.
(a) \left[ {\frac{n}{{n+3}}} \right]mgR
(b) \left[ {\frac{n}{{n-3}}} \right]mgR
(c) \left[ {\frac{n}{{n-1}}} \right]mgR
(d) \left[ {\frac{n}{{n+1}}} \right]mgR
Ans (d)
7.
If a body of mass m be projected vertically upward from the surface of the earth so as to reach a height nR above the earth’s surface. Calculate the velocity with which the body must be projected
(a) \sqrt{{\left( {\frac{n}{{n-1}}} \right)2gR}}
(b) \sqrt{{\left( {\frac{n}{{n+1}}} \right)2gR}}
(c) \sqrt{{\left( {\frac{n}{{n+1}}} \right)gR}}
(d) \sqrt{{\left( {\frac{n}{{n+1}}} \right)2R}}
Ans (b)
8.
A tunnel is dug along a diameter of the earth (mass = M). The force on a particle of mass m placed in the tunnel at a distance x from the centre is (R = radius of earth),
(a) \frac{{GMm}}{{{{R}^{3}}}}x
(b) \frac{{GMm}}{{{{R}^{2}}}}x
(c) \frac{{GMm}}{{{{R}^{3}}x}}
(d) \frac{{GMm}}{{{{x}^{2}}}}
Ans (a)
Practice Questions (JEE Main Level)
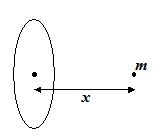
1.
A point mass m is at a distance x from the centre of a ring of mass M and radius R on its axis as shown in figure. Find the gravitational force between the two. What will this force be if x >>R and x <<R. For what value of x is the force maximum?
(a) ±R/ \sqrt{3}
(b) ±R/ \sqrt{5}
(c) ±R/ \sqrt{2}
(d) ±R/ \sqrt{8}
Ans (c)
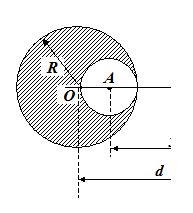
2.
A spherical cavity is made in a lead sphere of radius R such that its surface touches the outside surface of the lead sphere and passes through its centre. The mass of the lead before hollowing was M. What is the force of attraction that this sphere would exert on a particle of mass m which lies at a distance d from the centre of the lead sphere on the straight line joining the centers of the sphere and the hollow (as shown in the figure).
(a) \frac{{GMm}}{{{{d}^{2}}}}\left[ {3-\frac{1}{{5{{{\left[ {1-\left( {R/2d} \right)} \right]}}^{5}}}}} \right]
(b) \frac{{GMm}}{{{{d}^{2}}}}\left[ {1-\frac{1}{{8{{{\left[ {1-\left( {R/2d} \right)} \right]}}^{2}}}}} \right]
(c) \frac{{GMm}}{{{{d}^{2}}}}\left[ {3-\frac{1}{{8{{{\left[ {1-\left( {R/2d} \right)} \right]}}^{2}}}}} \right]
(d) \frac{{GMm}}{{{{d}^{2}}}}\left[ {3-\frac{1}{{5{{{\left[ {1-\left( {R/2d} \right)} \right]}}^{2}}}}} \right]
Ans (b)
3.
The gravitational field in a region is given by
\text{\vec{E}}=\left( {2\hat{i}+3\hat{j}} \right)N/kg
No work is done by the gravitational field when a particle is moved on the line
3y + kx = 5
The value of k should be
(a) 1
(b) 2
(c) 3
(d) 4
Ans (b)
Practice Questions (JEE Advance Level)
1.
Three particles, each of mass m are situated at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion.
(a) \sqrt{{\frac{{Gm}}{a}}}; \frac{{5\pi {{a}^{{-3/2}}}}}{{{{{\left( {3Gm} \right)}}^{{-1/2}}}}}
(b) \sqrt{{\frac{{Gm}}{a}}}; \frac{{2\pi {{a}^{{3/2}}}}}{{{{{\left( {3Gm} \right)}}^{{1/2}}}}}
(c) \sqrt{{\frac{{Gm}}{a}}}; \frac{{2\pi {{a}^{{2/3}}}}}{{{{{\left( {4Gm} \right)}}^{{1/2}}}}}
(d) \sqrt{{\frac{{Gm}}{a}}}; \frac{{2\pi {{a}^{{3/2}}}}}{{{{{\left( {3Gm} \right)}}^{{3/2}}}}}
Ans (b)
2.
Two concentric shells of masses M1 and M2 are situated as shown in the figure. Find the force on a particle of mass m when the particle is located at
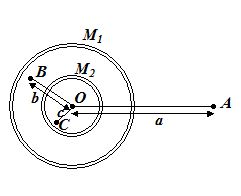
(a)
r = a
(a) Gm\left( {{{M}_{1}}+{{M}_{2}}} \right)/{{a}^{2}}
(b) Gm\left( {{{M}_{1}}+{{M}_{2}}} \right)/{{a}^{-2}}
(c) Gm\left( {{{M}_{1}}-{{M}_{2}}} \right)/{{a}^{2}}
(d) Gm\left( {{{M}_{1}}+{{M}_{2}}} \right)/{{a}^{-2}}
Ans (a)
(b)
r = b
(a) \left( {GMm/{{b}^{3}}} \right)
(b) \left( {GMm/2b} \right)
(c) \left( {GMm/{{b}^{2}}} \right)
(d) \left( {2GMm/b} \right)
Ans (c)
(c)
r = c.
(a)5
(b)20
(c)1
(d) 0
Ans (d)
The distance r is measured from the centre of the shell.
