Video Lecture
Theory For Notes Making
ACCELERATION DUE TO GRAVITY ON THE SURFACE OF EARTH
Consider a mass m placed on the surface of the earth of mass M. The mass experience a force F due to gravitation of earth
where F=GR2Mm
But the force with which a body is attracted towards the Earth gives the weight of the body.
∴ F = mg
∴ mg=GR2Mm or g=R2GM
Variation in acceleration due to gravity with height
Consider a body kept at a height h above the surface of earth. The force of attraction due to the earth on the body is F’. Where F’=G(R+h)2Mmbut F’=mg’
∴mg’=G(R+h)2Mm
hence g’=(R+h)2GM
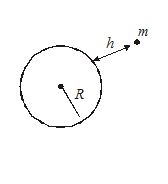
we know that at the surface of the earth, g=R2GM
On dividing g’ by g we get
gg’=(h+R)2R2
Henceg’=(h+R)2gR2 ——-(i)
( From the above equation we can find gravity at any height)
Variation of gravity with height
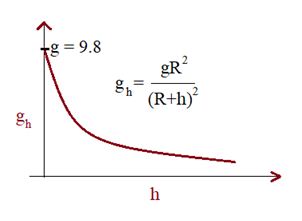
But also we can use an approximation to find gravity at a small height i.e. if h<<R as follows
g’=(h+R)2gR2 hence g’=(1+Rh)2g
So, with increase in height, g decreases. If h<<R.
g’=g[1+Rh]−2=g [1−R2h] (Use bionomial approximation)
hence g’=g [1−R2h]
so as height increases gravity decreases linearly for small heights.
Variation in acceleration due to gravity with depth
At the surface of the earth,
g=R2GM
for a point at a depth d below the surface,
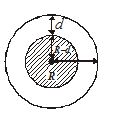
g’=R3GM [R−d] (see video lecture to reach this step)
gg’=(RR−d) i.e., g’=g [1−Rd]
So with increase in depth below the surface of the earth, g decreasing and at the center of the earth it becomes zero as shown in the graph given below.
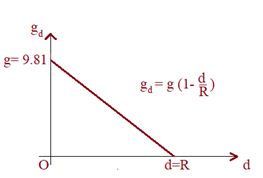
Comparison of height and depth for the same change in ‘g’
As we have seen above, the value of g decreases as we go above the surface of Earth or when we go below the surface of Earth. This can be taken to mean that value of g is maximum on the surface of Earth. hence gmax=R2GM
Now gh=g(1−R2h)and gd=g(1−Rd)
When gh=gd,then 1−R2h=1−Rd\−R2h=−Rd
or 2h=d or d=2h. Take care that this result is applicable for small heights only. Because while deriving the relation gh=g(1−R2h) we took this assumption that h<<R
Variation in acceleration due to gravity due to rotation of earth and latitude angle
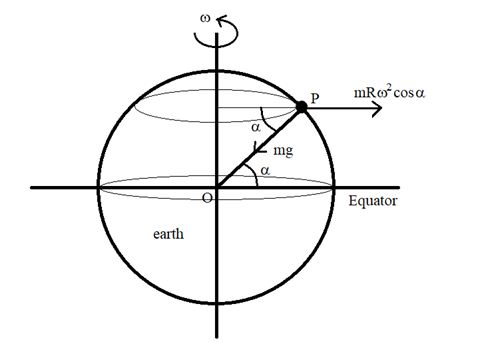
∴The earth is rotating about its axis from west to east. So, the earth is a non-inertial frame of reference. Every body on its surface experiences a centrifugal force mRw2 cosa. Where a is latitude of the place.
The net force on a particle on the surface of the earth is the resultant of these two forces which can be calculated by using law of parallelogram.
F = m2g2+m2ω4R2cos2α+2(mg)(mω2Rcosα)[cos(180−α)] (the angle between the two forces is 180 -a as clear from the diagram)
This net force produces the weight of the body hence F=mg’ ( where g’ is the net gravity at a latitude a
Therefore, mg’ = m2g2+m2ω4R2cos2α+2(mg)(mω2Rcosα)[cos(180−α)]
taking m2 as common from RHS and cancelling m from both sides we get g’=g2+ω4R2cos2α+2gω2Rcosα)[cos(180−α)]
hence g’=g2+ω4R2cos2α−2gω2Rcos2α)]
taking g2 as common on RHS
g’=g2[1+g2ω4R2cos2α−g22gω2Rcos2α] ⇒g’=g[1+g2ω4R2cos2α−g2ω2Rcos2α]
here w is the angular velocity of rotation of earth about its own axis which can be given as
ω=T2π=24hrs2π=24×60×60sec2π=0.0000727rad/sec. hence it Is a very small number therefore w4 becomes negligible so the whole term g2ω4R2cos2α from the above equation of g’ can be neglected hence we get g’=g[1−g2ω2Rcos2α]1/2
again here gω2Ris a small term so we can use binomial approximation and can write the above equation of g’ as follows
g’=g[1−21×g2ω2Rcos2α]
⇒g’=g[1−gω2Rcos2α]
hence finally we get g’=g−ω2Rcos2α
Important points to remember
(i) at the pole, a = 90°cos a = minimum = 0 hence g’ is maximum and is equal to g
(ii) at equator a = 0°, so g’ is minimum and is equal to g-w2R
(iii) due to rotation of earth the gravity on the surface is decreased except at poles.
Example-5:
Calculate the acceleration due to gravity at the surface of Mars if its diameter is 6760 km and mass one tenth that of the earth. The diameter of earth is 12742 km and acceleration due to gravity on the earth is 9.8 m/s2.
Solution:
We know that
g=R2GM
gEgM=(MEMM)(RMRE)2=[101] [676012742]2
or, gEgM=0.35
gM = 0.35 x gE = 9.8 x 0.35 = 3.48 m/s2
Illustration
A simple pendulum of length one metre is taken to a height R, which is the radius of earth. If the acceleration due to gravity on the surface of earth is p2 m/s2, what is the period of the pendulum at this height?
(a) 1 s (b) 2 s
(c) 3 s (d) 4 s
Solution
As we know that time period of simple pendulum i.e. T = 2πgl
Where g is acceleration due to gravity on the surface of earth and is given as π2 m/s2.
At height R the acceleration due to gravity
i.e g’ = 4π2 m/s2
∴ T=2π(π2/4)1=4s
(d)
Illustration
A planet has twice the density of earth but the acceleration due to gravity on its surface is exactly the same as on the surface of earth. Its radius in terms of earth R will be
(a) R/4
(b) R/2
(c) R/3
(d) R/8
Solution
We have g = R2GM=R2G[34πR3ρ]
where r is the density of the earth.
For the planet g’ =(R’)2G[34πR‘3(2ρ)]
According to the question
g = g’
R2G[34πR3ρ]=R‘2G×34πR‘3(2ρ)
R’ = 2R
(b)
Objective Assignment
1.
Considering the earth to be a homogeneous sphere. Scientist A goes deep down in a mine and scientist B goes high up in a balloon. The gravitational field measured by
(a) A goes on decreasing and that B goes on increasing
(b) Both A and B goes on increasing
(c) B goes on decreasing and that by A goes on increasing
(d) Both A and B goes on decreasing
Ans (d)
2.
As we go from equator to the poles the value of g
(a) remains the same
(b) decreases
(c) increases
(d) decreases upto a latitude of 45° and then increases
Ans (c)
3.
A planet has twice the values of mass and radius of earth. Acceleration due to gravity on the surface of the planet is
(a) 9.8 m/sec2
(b) 4.9 m/sec2
(c) 980 m/sec2
(d) 19.6 m/sec2
Ans (b)
4.
The value of g will be 1% of its value at the surface of earth at a height of (Re= 6400 km)
(a) 6400 km
(b) 57600 km
(c) 2560 km
(d) 64000 km
Ans (b)
5.
The variation of acceleration due to gravity as one moves away from earth centre is given by
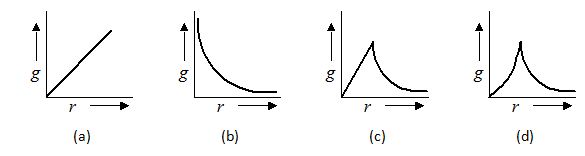
Ans (c)
Subjective Assignment
1.
At what height over the Earth’s pole the free-fall acceleration decreases by one per cent; by half?
Ans 32 km, 2650 km.
