Video Lecture
Theory For Making Notes
TORQUE
Torque is the rotational analog of force
Force causes linear acceleration; torque causes angular acceleration.
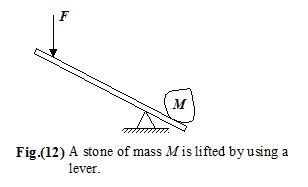
In order to lift a stone by using a lever, a force is required (see figure 12). The effectiveness of the force depends both on its direction and where it is applied relative to the pivot point.
The turning ability of a force about an axis or pivot is called its torque.
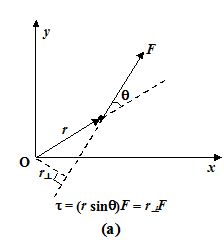
The torque of a force F that acts at a distance r from the origin is defined as
t = rF sinθ (20)
Where θ is the angle between the vector r and F, as shown in the figure (13)
The definition of torque (equation 20) may be interpreted in two ways:
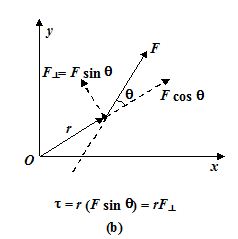
(i) t = r (Fsinθ) = r F⊥
The turning effect of a force about the origin is produced only by the perpendicular component (F⊥ = F sin θ) as shown in the figure (b).
(ii) t = (r sinθ) F = r⊥ F
Where r⊥ is the perpendicular distance from the origin to the line of action of the
force as shown in the figure (a). It is also called the lever arm.
The Torque Equation
If the net torque acting on a body about any inertial axis is \vec{\tau } and the moment of inertia about that axis is I, then the angular acceleration \vec{\alpha } of the body is given by the relation: \vec{\tau }=I\,\vec{\alpha }.
If the axis is non-inertial, the equation \vec{\tau }=I\,\vec{\alpha } is applicable but net torque \vec{\tau } also includes the torque of pseudo force about the non-inertial axis.
Proof:
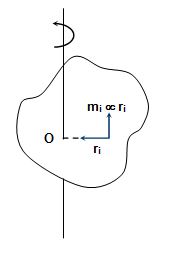
{{\vec{\tau }}_{O}}= \Sigma {{\vec{r}}_{{iO}}}\times \left( {{{{\vec{f}}}_{r}}+{{{\vec{f}}}_{t}}} \right)
= \Sigma {{\vec{r}}_{{iO}}}\times {{\vec{f}}_{r}} \Sigma {{\vec{r}}_{{iO}}}\times {{\vec{f}}_{r}} + \Sigma {{\vec{r}}_{{iO}}}\times {{\vec{f}}_{t}}
= 0 + \Sigma {{\vec{r}}_{{i0}}}\times {{\vec{f}}_{t}}
= \Sigma {{\vec{r}}_{{iO}}}\times ({{m}_{i}}{{\vec{a}}_{t}})
= \Sigma {{\vec{r}}_{{iO}}}\times ({{m}_{{iO}}}\vec{\alpha }\times {{\vec{r}}_{{iO}}})
Angle between \vec{\alpha } and \vec{r} is 90° and \vec{\alpha } ´ \vec{r} is ^ to \vec{r}.
{{\vec{\tau }}_{O}}= \Sigma {{m}_{{iO}}}r_{{iO}}^{2}\vec{\alpha } = {{\vec{I}}_{O}}\vec{\alpha }
When the axis is passing through C.M. of rigid body, then we can use the torque equation
\displaystyle {{\tau }_{{cm}}}={{I}_{{cm}}}\alpha
where τcm is the net torque of real forces acting on the body about C.M. axis whether it is accelerating or non-accelerating. Because when it is accelerating the torque of pseudo force acting on C.M. will be zero.
Newton’s Second Law
Since torque is a rotational analog of force, therefore, Newton’s second law for rotational motion is given by
τnet = Ia (21)
Note that the above equation (21) is not a vector equation.
It is valid in two situations:
(i) The axis is fixed in position and direction.
(ii) The axis passes through the center of mass and is fixed in direction only.
The equation τcm = Icmacm (22)
is valid even if the center of mass is accelerating.
Illustration
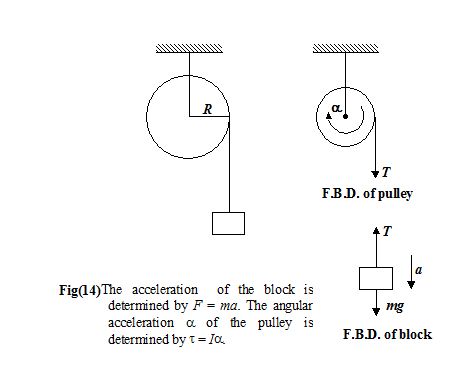
A disc-shaped pulley has mass M = 4 kg and radius R = 0.5 m. It rotates freely on a horizontal axis, as in figure (14). A block of mass m = 2 kg hangs by a string that is tightly wrapped around the pulley.
(a) What is the angular velocity of the pulley 3 s after the block is released?
(b) Find the speed of the block after it has fallen 1.6m. Assume the system starts at rest.
Solution
Since the string is tangential to the pulley, the torque on it due to the tension is t = TR. The two forms of Newton’s second law for the block and the pulley yield
Block (F = ma) mg – T = ma
Pulley (t = Ia) TR = \left( {\frac{1}{2}M{{R}^{2}}} \right)\alpha
Applying Newton’s second Law
τ = Ia
For the disc, I = \frac{{M{{R}^{2}}}}{2}
TR = \left( {\frac{{M{{R}^{2}}}}{2}} \right)\alpha or T = \frac{{MR\alpha }}{2} (i)
Applying Newton’s second Law on the block
Fnet = ma
mg – T = ma (ii)
Since the block and the rim of the pulley have the same speed (the string does not slip), we have v = ωR and a = αR. Thus, from equation (i) we find
T = \frac{1}{2}Ma (iii)
Adding (ii) and (iii) leads to
a = \frac{{mg}}{{m+\frac{M}{2}}} (iv)
Putting m = 2 kg; M = 4 kg; R = 0.5m;
we get a = 5 m/s2
(a) To find w after 3 s, we use equation (9)
ω = ωo + at = 0 + \left( {\frac{a}{R}} \right)t=30 rad/s
(b) To find the speed of the block we use
v2 = vo2 + 2ay = 0 + 2(5 m/s2)(1.6 m)
Thus v = 4 m/s
Rotational Work and Energy Board
The rotational work done by a force about the fixed axis of rotation is defined as
Wrot = \int{{\tau d\theta }} (23)
Where t is the torque produced by the force, and dq is the infinitesimally small angular displacement about the axis.
The rotational kinetic energy of a body about a fixed rotational axis is defined as
Krot = \frac{1}{2} Iw2 (24)
where I is the moment of inertia about the axis.
Work – Energy Theorem
In complete analog to the work energy theorem for the translatory motion, it can be stated for rotational motion as:
Wrot = ΔKrot (25)
The net rotational work done by the forces is equal to the change in rotational kinetic energy of the body.
Conservation of Mechanical Energy
In the absence of dissipative work done by non-conservative forces, the total mechanical energy of a system is conserved.
ΔK + ΔU = 0
or Kf + Uf = Ki + Ui (26)
Rotational Power
In complete analog with the linear motion, the instantaneous rotational power is defined as
Prot = \frac{{d{{W}_{{rot}}}}}{{dt}}=\text{ }\!\!\tau\!\!\text{ }\text{. }\!\!\omega\!\!\text{ } (27)
Illustration
A motor rotates a pulley of radius 25 cm at 20 rpm. A rope around the pulley lifts a 50 kg block, as shown in figure. What is the power output of the motor?
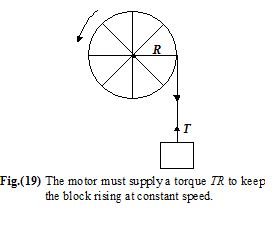
Solution
The tension in the rope is equal to the weight since there is no acceleration.
Thus, τ = 500 N.
Therefore, τ = TR = (500)(0.25)
= 125 Nm.
Angular velocity, ω = \frac{{2\pi N}}{{60}}
or ω = \frac{{2\pi \left( {20} \right)}}{{60}}=\frac{{2\pi }}{3}rad/s
The power required is
P = t ω = (125 N m) \left( {\frac{{2\pi }}{3}rad/s} \right)=260\,W
Force and torque equations for a rigid body in plane motion
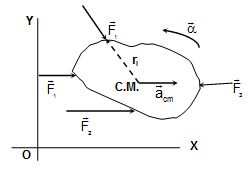
(i) ∑ (External forces) = mass of the body ´ acceleration of the centre of mass
∑ \displaystyle ({{\vec{F}}_{i}})=M{{\vec{a}}_{{cm}}}
(ii) ∑ (moments of external forces about the C.M. axis)
= moment of inertia of the body about the C.M. axis
´ angular acceleration about the C.M. axis
\displaystyle \sum{{({{{\vec{r}}}_{i}}\times {{{\vec{F}}}_{i}}).\hat{k}={{I}_{{cm}}}\alpha }}
Illustration
A uniform rod of length l and mass m is suspended on two vertical inextensible string as shown in the figure. Calculate tension T in left string at the instant, when right string snaps.
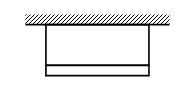
Let the tension in the rope be T and the acceleration of the centre of mass of the rod downwards be a.
Then mg – T = ma . . . (1)
Again, \displaystyle \frac{{\text{mg}\ell }}{\text{2}}= Ia = \displaystyle \frac{{\text{m}{{\ell }^{\text{2}}}}}{\text{3}} ´ \displaystyle \frac{{2a}}{\ell }
a = \displaystyle \frac{{3g}}{4} . . . (2)
T = \displaystyle \frac{{mg}}{4}
Hence, (C) is correct.
Practice Questions (Level-1)
1.
On a body a force \overrightarrow{{F\,}} is applied such that its line of action passes through axis of rotation. In such case torque due to force \overrightarrow{{F\,}}will be
(a) always zero
(b) always non-zero
(c) positive
(d) negative
Ans (a)
2.
If a body is rotating with angular acceleration a. Then value of a is given by
(a) \frac{{d\theta }}{{d\omega }}
(b) \frac{{d\omega }}{{d\theta }}
(c) \int{{\omega dt}}
(d) \frac{{\omega d\omega }}{{d\theta }}
Ans (d)
Where w is angular velocity, t is time and q is angular displacement.
3.
Two forces each of magnitude F is applied on the rod of length l which is hinged at one end. Find magnitude of net torque
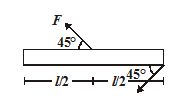
(a) \frac{{3Fl}}{{2\sqrt{2}}}
(b) \frac{{Fl}}{{\sqrt{2}}}
(c) zero
(d) \frac{{Fl}}{{2\sqrt{2}}}
Ans (d)
4.
A disc is rotating with an angular velocity \overrightarrow{\omega }.A force \overrightarrow{F} acts at a point whose position vector with respect to axis of rotation is \overrightarrow{{r\,}}. The power associated with the torque due to the force is given by
(a) (\overrightarrow{{r\,}}\times \overrightarrow{F}).\overrightarrow{\omega }
(b) (\overrightarrow{{r\,}}\times \overrightarrow{F})\times \overrightarrow{\omega }
(c) \overrightarrow{{r\,}}.(\overrightarrow{{F\,}}\times \overrightarrow{\omega })
(d) \overrightarrow{{r\,}}\times (\overrightarrow{{F\,}}.\overrightarrow{\omega })
Ans (a)
5.
A disc is free to rotate about a fixed axis through the centre. A force F is applied. What is the direction of torque about O, the centre of disc, due to \overrightarrow{F}?
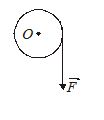
(a) Towards the bottom of the page
(b) Up out of page
(c) Towards the right hand edge of the page
(d) Down into the page
Ans (d)
6.
Two force are applied on the string and string move without slipping on pulley of mass m and radius R. Considering pulley as solid cylinder find its angular acceleration
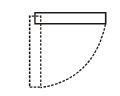
(a) \frac{{\sqrt{{3gl}}}}{2}
(b) \sqrt{{2gl}}
(c) \sqrt{{gl}}
(d) none of these
Ans (a)
8.
A wheel of moment of inertia I and rotating with angular velocity w is stopped in time t. Its angular retardation is
(a) \frac{\omega }{{2t}}
(b) \frac{\omega }{t}
(c) \frac{{I\omega }}{{2t}}
(d) \frac{{I\omega }}{t}
Ans (b)
9.
A stone of mass m is rotating along a circular path with constant speed v on a horizontal table. If the radius of circular path is r then torque acting on it is
(a) zero
(b) \frac{{m{{v}^{2}}}}{r}(2r)
(c) \left( {\frac{1}{2}m{{v}^{2}}} \right)\ \left( {\frac{{2r}}{r}} \right)
(d) none of these
Ans (a)
10.
A force of (3\hat{i}\,+\,4\hat{k})N is acted upon a flywheel tangentially. The radius vector of the flywheel is (2\hat{j}\,-\,4\hat{k})m. The torque acting on the flywheel is
(a) 25 N–m
(b) 20.6 N–m
(c) \sqrt{{42}}\,\text{N}-\text{m}
(d) none of these
Ans (b)
11.
A wheel, whose moment of inertia is 0.03 kg m2, is accelerated from rest to 20 rad/s in 5s. When the external torque is removed, the wheel stops in 1 min. Find:
(a) the frictional torque
(a)0.10 Nm
(b)0.01 Nm
(c)0.1 Nm
(d)0.20 Nm
Ans (b)
(b) the external torque
(a)0.15 Nm
(b)0.20 Nm
(c)0.10 Nm
(d)0.13 Nm
Ans (d)
Practice Questions (Level-2)
1.
Two men support a uniform horizontal thin rod of weight W at its two ends. If one of them suddenly lets the rod go, the force exerted by the rod on the other man will be
(a) W
(b) \frac{W}{2}
(c) \frac{W}{4}
(d) zero
Ans (c)
2.
A rod of mass m is hinged at point O and it is kept in equilibrium by support of a wedge below it. Find force exerted by wedge on the rod.
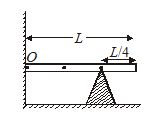
(a) \frac{{mg}}{2}
(b) \frac{{3mg}}{2}
(c) \frac{{2mg}}{3}
(d) mg
Ans (c)
3.
A tangential force acting on solid sphere of radius 2 m varies with time (in micro second) as shown in the figure. The magnitude of total angular impulse on the body due to this force to this force is
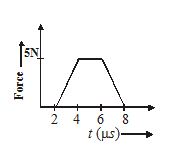
(a) 2\times {{10}^{{-5}}}\text{Nms}
(b) 4\times {{10}^{{-6}}}\text{Nms}
(c) 2\times {{10}^{{-6}}}\text{Nms}
(d) 4\times {{10}^{{-5}}}\text{Nms}
Ans(d)
4.
A rod of length ‘L’ whose lower end is fixed the horizontal plane starts to topple from the vertical position. The velocity of the upper end of the rod when it hits the ground is:
(a) \sqrt{{gh}}
(b) \sqrt{{3gL}}
(c) \sqrt{{5gL}}
(d) \sqrt{{7gl}}
Ans (b)
5.
A uniform rod of mass M and length L is pivoted about an axis perpendicular to the rod at a distance L/4 from one end. Find the moment of inertia of the rod about this axis.
(a) \frac{{2M{{L}^{-2}}}}{{48}}
(b) \frac{{7M{{L}^{2}}}}{{48}}
(c) \frac{{7M{{L}^{-3}}}}{{45}}
(d) \frac{{7M{{L}^{2}}}}{{24}}
Ans (b)
6.
A cord is wrapped around the rim of a flywheel 0.5m in radius. The wheel is mounted in frictionless bearings on a horizontal shaft through its centre. The moment of inertia of the wheel is 4 kg-m2. If a block having a mass of 5 kg hangs from the cord, calculate the angular acceleration of the wheel.
(a) 1.66 rad/s2
(b) 2.59 rad/s2
(c) 2.45 rad/s2
(d) 4.66 rad/s2
Ans(d)
7.
In the given figure, m1 slides without friction on the horizontal surface. The frictionless pulley is in the form of a solid cylindrical disc of mass M and the radius R, and the string turns the pulley without slipping. Find the tension T2 in the string.
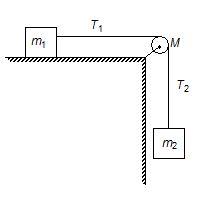
(a) \ {{T}_{2}}=\frac{{(3{{m}_{1}}{{m}_{1}}+M{{m}_{2}})\ g}}{{2{{m}_{3}}+2{{m}_{2}}+M}}
(b) \ {{T}_{2}}=\frac{{(2{{m}_{1}}{{m}_{2}}+M{{m}_{2}})\ g}}{{2{{m}_{1}}+2{{m}_{2}}+M}}
(c) \ {{T}_{1}}=\frac{{(2{{m}_{1}}{{m}_{2}}+M{{m}_{2}})\ g}}{{2{{m}_{9}}+2{{m}_{5}}+M}}
(d) \ {{T}_{1}}=\frac{{(5{{m}_{1}}{{m}_{6}}+M{{m}_{2}})\ g}}{{2{{m}_{1}}+2{{m}_{2}}+M}}
Ans (d)
Comprehension Based Question (8 and 9)
A block of mass 2 kg can slide down a frictionless 53° incline but it is connected to a pulley of mass
M = 4 kg and radius R = 0.5 m, as shown in the figure. The pulley can be treated as disc. Find
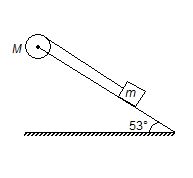
8.
the angular acceleration of the pulley
(a) 4.03 rad/s2
(b) 3.50 rad/s2
(c) 3.98 rad/s2
(d) 2.68 rad/s2
Ans (c)
9.
the speed of the block after it has slide 1m, starting from rest.
(a) 2.8 m/s
(b) 3.5 m/s
(c) 2.5 m/s
(d) 1.2 m/s
Ans (a)
10.
A block of mass 4 kg suspended by a rope that passes over a pulley of mass 2 kg radius 5cm. The rope is connected to a spring whose stiffness constant is 80 N/m.
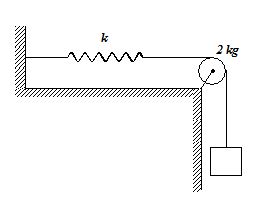
(a) If the block is released from rest, what is the maximum extension of the spring?
(a) 0.86 m
(b) 0.98 m
(c) 0.2 m
(d) 0.50 m
Ans (b)
(b) What is the speed of the block after it has fallen 20 cm? Treat the pulley as a disc.
(a) 1.50 m/s
(b) 1.20 m/s
(c) 1.00 m/s
(d) 1.58 m/s
Ans (d)
11.
A horizontal force F = 140 N is applied to a 35 kg crate of width b = 50 cm and height h = 1.1 m that is on a horizontal surface.
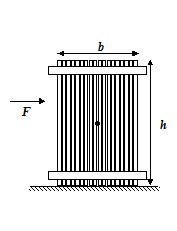
(a) What is the maximum distance above the floor that F can be applied without tipping the crate? Assume that the crate does not slip.
(a) 0.230 m
(b) 0.613 m
(c) 0.500 m
(d) 0.630 m
Ans (b)
(b) If F is applied at the level of center of gravity of the crate, what is the effective point of application of the resultant normal force due to the floor?
(a) 0.224 m
(b) 0.20 m
(c) 0.11 m
(d) 0.358 m
Ans (a)
