Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-1)
1.
A block slides down an inclined plane of slope angle q with constant velocity. It is then projected up the same plane with an initial velocity vo. How far up the incline will it move before coming to rest.
(a)\frac{{v_{o}^{3}}}{{4g\sin \theta }}
(b)\frac{{v_{o}^{5}}}{{4g\sin \theta }}
(c)\frac{{v_{o}^{2}}}{{4g\sin \theta }}
(d)\frac{{v_{o}^{2}}}{{4g\cos \theta }}
Ans (c)
Comprehension Based Question (2 to 4)
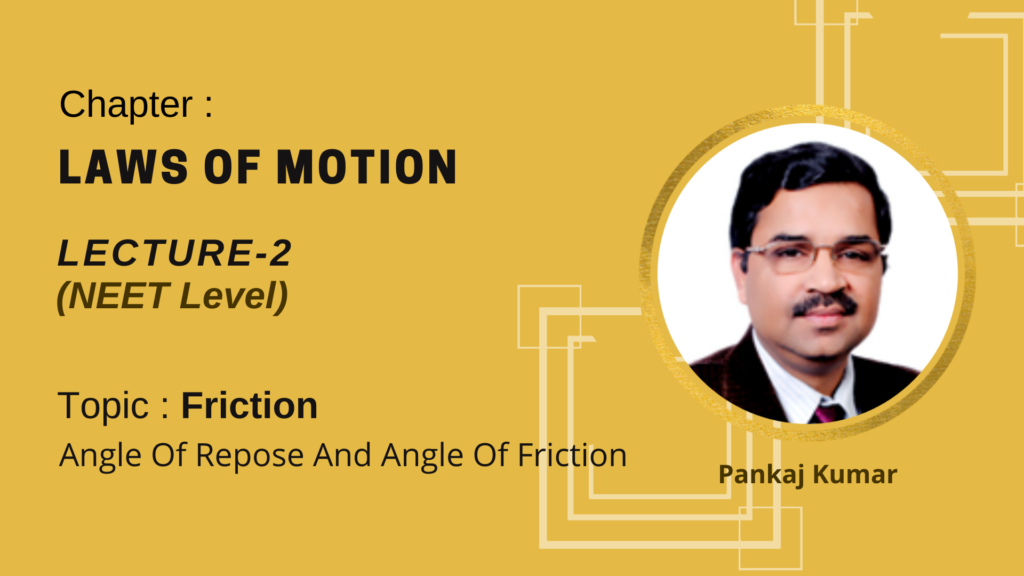
Block A of mass m and block B of mass 2m are placed on a fixed triangular wedge by means of a massless, inextensible string and a frictionless pulley as shown in figure. The wedge is inclined at 45° to the horizontal on both sides. The coefficient of friction between block A and the wedge is 2/3 and that between block and the wedge is 1/3. If the system of A and B is released from rest, find
2.
the acceleration of A
(a)10
(b)2
(c)0
(d)1.25
Ans (c)
3.
tension in the string, and (a)
(a) (3√2/3) mg
(b)(2√2/3) mg
(c)(2√2/7) mg
(d)(5√2/2) mg
Ans (b)
4.
The magnitude and direction of the force of friction acting on A.
(a)(mg/√2)
(b)(mg/5√2)
(c)(mg/2)
(d)(mg/3√2)
Ans (d)
Practice Questions (Level-2)
1.
How high can a particle rest inside a hollow sphere of radius aif the coefficient of friction be µ= 1/√3
(a)0.011 a
(b)0.134 a
(c)0.150 a
(d)1.0 a
Ans (b)
2.
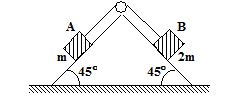
The system shown below uses massless pulleys and rope. The coefficient of friction between the masses and horizontal surfaces is µ. Assume that M1 and M2 are sliding and gravity is directed downward.Find the tension in the rope.
(a)\frac{{(\mu +1)\,g}}{{\frac{2}{{{{M}_{3}}}}\,+\,\frac{1}{{1{{M}_{2}}}}\,+\frac{1}{{3{{M}_{5}}}}}}
(b)\frac{{(\mu)\,g}}{{\frac{3}{{{{M}_{3}}}}\,-\,\frac{1}{{2{{M}_{1}}}}\,+\frac{2}{{1{{M}_{2}}}}}}
(c)\frac{{(\mu -1)\,g}}{{\frac{2}{{{{M}_{3}}}}\,+\,\frac{1}{{2{{M}_{1}}}}\,-\frac{2}{{1{{M}_{2}}}}}}
(d)\frac{{(\mu +1)\,g}}{{\frac{2}{{{{M}_{3}}}}\,+\,\frac{1}{{2{{M}_{1}}}}\,+\frac{1}{{2{{M}_{2}}}}}}
Ans (d)
3.
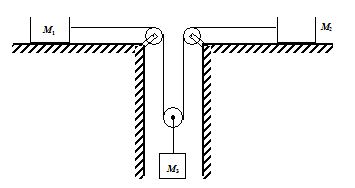
The coefficient of static friction between block and the horizontal surface is 0.25. Find the maximum weight of block A for which the system will be stationary. The block B weighs 700 N.
(a) 100 N
(b) 500 N
(c) 1000 N
(d) 0 N
Ans (a)
4.
Two blocks with masses m and M are not attached. The coefficient of static friction between the blocks is µ and the horizontal surface is frictionless. What is the minimum magnitude of the horizontal force required to hold m against M.
(a)\frac{{m(M+m)g}}{{\mu M}}
(b)\frac{{m(M-m)g}}{{\mu M}}
(c)\frac{{m(2M+m)g}}{{\mu 2M}}
(d)\frac{{m(M+m)g}}{{\mu M}}
Ans (d)
Comprehension Based question ( 5 and 6)
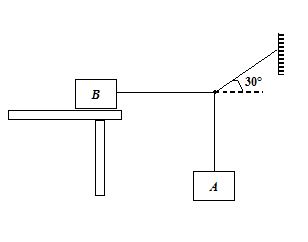
A block of mass m = 2 kg is placed on a block of mass M = 4kg as shown in the figure.The coefficient of kinetic friction for all surfaces is µk =0.2. Ignore the masses of the pulley and the rope. For what value of the horizontal force F will the blocks
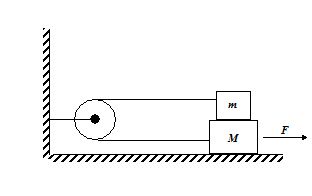
5.
move at constant speed
(a) 50N
(b) 30 N
(c) 20 N
(d) 0
Ans (C)
6.
accelerate at 2 m/s2
(a) 30 N
(b) 32 N
(c) 36 N
(d) 40 N
Ans (b)
Comprehension Based Question ( 7 to 9)
In the figure shown, the mass m2 = 10 kg slides on a frictionless table. The coefficients of static and kinetic friction between m2 and m1 = 5 kg are µs = 0.6 and µk = 0.4
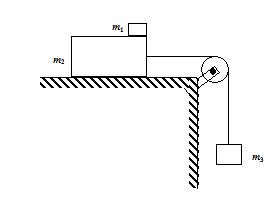
7.
What is the maximum acceleration of m1?
(a) 5 g
(b) 2 g
(c) 0.6 g
(d) 0.2 g
Ans (c)
8.
What is the maximum value of m3 if m1 moves with m2 without slipping ?
(a) 20.0 kg
(b) 22.5 kg
(c) 23.5 kg
(d) 25.0 kg
Ans (b)
9.
If m3 =30 kg, find the acceleration of each body and the tension in the string.
(a) 0.7 g for m2 and m3 1.4g for m1; 9g N
(b) 0.7 g for m2 and m3 2.2g for m1; 9g N
(c) 0.7 g for m2 and m3 0.8g for m1; 9g N
(d) 0.7 g for m2 and m3 1.0 g for m1; 9g N
Ans (d)
Comprehension Based Question (10 to 12)
A block rest on a rough inclined plane as shown. A horizontal force is applied to it
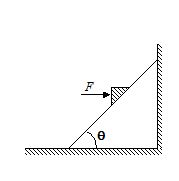
10.
Find out the force of reaction,
(a) R = mg cos q + F sin q
(b) R = mg cos q – F sin q
(c) R = mg cos q / F sin q
(d) R = mg cos 90 + F sin 90
Ans (a)
11.
Can the force of friction be zero if yes when? and
(a) Yes, if mg sin q = F cos q
(b) No, if mg sin q = F cos q
Ans (a)
12.
Assuming that friction is not zero find its magnitude and direction of its limiting value.
Ans = mR = m(mg cos q + F sin q); up the plane if the body has tendency to slide down and down the plane if the body has tendency to move up)