Video Lecture
Theory For Making Notes
Constraints imply that two bodies which are inter connected are not free to move but their accelerations are mutually linked. Constrained relations are equations that show how the motions of a system of bodies relate to one another. The geometric limitations placed on a body’s mobility that also control its trajectory are known as constraints. To link the accelerations between the bodies, we must apply the constraint equations method. Initially, we begin our examination with basic pulley situations.
Two blocks of mass m1 and m2 are attached at the ends of an inextensible string, which passes over a smooth massless pulley. If m1 > m2, find
(a) the acceleration of each block
(b) the tension in the string.
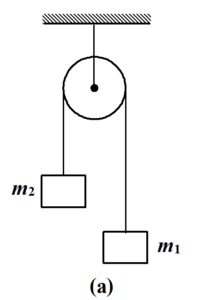
Solution
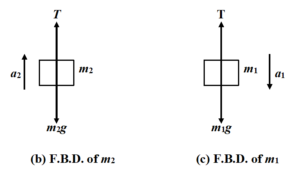
The free body diagram of each block is shown in the figure.
Note
- The block m1 is assumed to be moving downward and the block m2 is assumed to be moving upward. It is merely an assumption and it does not imply the real direction of motion. If the values of a1 and a2 come out to be positive then only the assumed directions are correct; otherwise the bodies move in the opposite directions.
- Since the pulley is smooth and massless, therefore, the tension on each side of the pulley is same.
Applying Newton’s second Law on
Block m1 m1g – T = m1a1 ..(i)
Block m2 –m2g + T = m2a2 ..(ii)
Number of unknowns : T, a1 and a2 (three)
Number of equations : only two
Obviously, we require one more equation to solve the problem. Note that the whenever one finds the number of equations less than the number of unknowns, one must think about the constraint relation. In the previous problems we have obtained the constraint relation by experience and judgement. Now we are going to explain the mathematical procedure for this.
How to determine Constraint Relation ?
- Assume the direction of acceleration of each block, e.g. a1 (downward) and a2 (upward) in this case.
- Locate the position of each block from a fixed point (depending on convenience), e.g. centre of the pulley in this case.
- Identify the constraint and write down the equation of constraint in terms of the distance assumed.
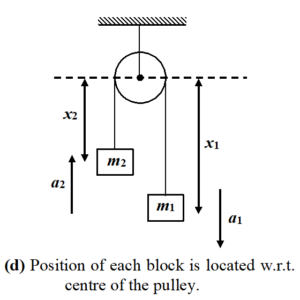
For example consider a pulley system with two masses connected through a string which passes over the pulley. lets find the constraint equation.
in the chosen problem, the length of string remains constant and it is the constraint or restriction.
Thus, length of string (L) = x1 + x2 = constant
Differentiating both the sides w.r.t. time, we get
\frac{{d{{x}_{1}}}}{{dt}}\,+\frac{{d{{x}_{2}}}}{{dt}}\,\,=0
Each term on the left side represents velocity of the block.
Since we have to find a relation between accelerations, therefore, we differentiate it once again w.r.t. time.
Thus \frac{{{{d}^{2}}{{x}_{1}}}}{{d{{t}^{2}}}}+\frac{{{{d}^{2}}{{x}_{2}}}}{{d{{t}^{2}}}}=0
Since the block m1 is assumed to be moving downward (x1 is increasing with time)
\frac{{{{d}^{2}}{{x}_{1}}}}{{d{{t}^{2}}}}\,=+{{a}_{1}}, a1 > 0
and block m2 is assumed to be moving upward (x2 is decreasing with time)
\frac{{{{d}^{2}}{{x}_{2}}}}{{d{{t}^{2}}}}\,=-\,{{a}_{2}}, a2 > 0
Thus a1 – a2 = 0
or a1 = a2 = a
Alternative method,
one can also assume the distance of each block from the ground as shown in the figure.
One can easily see that an expression for length of the string can not be written unless we locate the centre of the pulley w.r.t. ground.
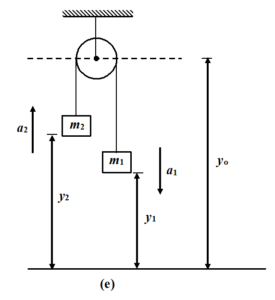
If y0 be the distance of the ground from the centre of the pulley then the length of string is
(y0 –y1) + (y0 – y2) = constant
2y0 – y1 – y2 = constant
Differentiating twice w.r.t. time, we get
0 – \frac{{{{d}^{2}}{{y}_{1}}}}{{d{{t}^{2}}}}\,-\,\frac{{{{d}^{2}}{{y}_{2}}}}{{d{{t}^{2}}}}\,=0
Now, \frac{{{{d}^{2}}{{y}_{1}}}}{{d{{t}^{2}}}}\,=-{{a}_{1}} and \frac{{{{d}^{2}}{{y}_{2}}}}{{d{{t}^{2}}}}\,=+\,{{a}_{2}}
Thus a1 – a2 = 0
a1 = a2 = a
Substituting a1 = a2 = a in equations (i) and (ii) and after solving them, we get
a = \left[ {\frac{{{{m}_{1}}\,-{{m}_{2}}}}{{{{m}_{1}}\,+{{m}_{2}}}}} \right]\,g also T = \left[ {\frac{{2{{m}_{1}}\,{{m}_{2}}}}{{{{m}_{1}}\,+{{m}_{2}}}}} \right]\,g
Illustration
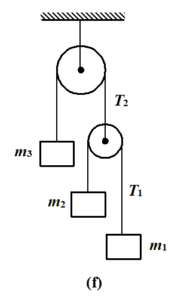
A system of three masses m1, m2 and m3 are shown in the figure. The pulleys are smooth and massless; the strings are massless and inextensible.
(a) Find the tensions in the strings
(b) Find the acceleration of each mass.
Solution
All the blocks are assumed to be moving downward and the free body diagram of each block is shown in the figure
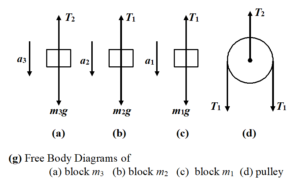
Applying Newton’s Second Law on
Block m1 m1g – T1 = m1a1 ..(i)
Block m2 m2g – T1 = m2a2 ..(ii)
Block m3 m3g – T2 = m3a3 ..(iii)
Pulley T2 = 2T1 ..(iv)
Number of unknowns : a1, a2, a3, T1 and T2 (Five)
Number of equations : Four
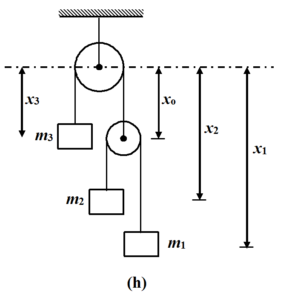
The constraint relation among accelerations can be obtained as follows
For upper string:
x3 + x0 = c1
For lower string:
(x2 – x0) + (x1 – x0) = c2
x2 + x1 – 2x0 = c2
Eliminating x0 from the above two equations, we get
x1 + x2 + 2x3 = 2c1 + c2 = constant
Differentiating twice with respect to time.
we get
\frac{{{{d}^{2}}{{x}_{1}}}}{{d{{t}^{2}}}}\,+\frac{{{{d}^{2}}{{x}_{2}}}}{{d{{t}^{2}}}}\,+\,2\,\frac{{{{d}^{2}}{{x}_{3}}}}{{d{{t}^{2}}}}\,=0
or a1 + a2 + 2a3 = 0 …(v)
After solving equations (i) to (v), we get
T1 = \left[ {\frac{{4\,{{m}_{1}}{{m}_{2}}{{m}_{3}}}}{{4{{m}_{1}}{{m}_{2}}\,+{{m}_{{3\,}}}({{m}_{1}}\,+{{m}_{2}})}}} \right]g; T2 = 2T1
a1 = \left[ {\frac{{4\,{{m}_{1}}{{m}_{2}}\,+\,{{m}_{1}}{{m}_{3}}\,-\,3\,{{m}_{2}}{{m}_{3}}}}{{4{{m}_{1}}{{m}_{2}}\,+{{m}_{3}}({{m}_{1}}\,+{{m}_{2}})}}} \right]g
a2 = \left[ {\frac{{3\,{{m}_{1}}{{m}_{3}}\,-\,{{m}_{2}}{{m}_{3}}\,-\,4\,{{m}_{1}}{{m}_{2}}}}{{4{{m}_{1}}{{m}_{2}}\,+{{m}_{3}}({{m}_{1}}\,+{{m}_{2}})}}} \right]g
a3 = \left[ {\frac{{4\,{{m}_{1}}{{m}_{2}}\,-\,{{m}_{3}}\,(\,{{m}_{1}}+{{m}_{2}})}}{{4{{m}_{1}}{{m}_{2}}\,+{{m}_{3}}({{m}_{1}}\,+{{m}_{2}})}}} \right]g
Illustration
Find the relation between the accelerations of two bodies shown in the figure.
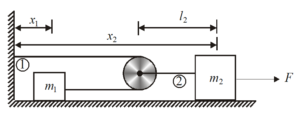
({{x}_{2}}-{{l}_{2}})+({{x}_{2}}-{{l}_{2}}-{{x}_{1}})=L (length of string)
Differentiating twice w.r.t time t. \frac{{{{d}^{2}}{{x}_{2}}}}{{d{{t}^{2}}}}+\frac{{{{d}^{2}}{{x}_{2}}}}{{d{{t}^{2}}}}-\frac{{{d}^{2}{{x}_{1}}}}{{d{{t}^{2}}}}=0
here {{l}_{2}} and L are constant
hence {2{{a}_{2}}-{{a}_{1}}=0}
Illustration
Consider a system of two blocks A and B connected together with an inextensible string as shown in figure. Determine the relation between their accelerations?
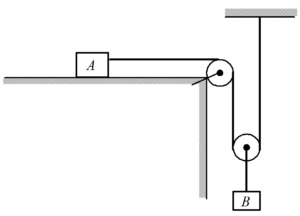
Solution
Let us assume the respective distance of each block as shown in figure. Note that the acceleration of block B is equal to that of the centre of the lower pulley. Therefore, centre of this pulley is located instead of the block B. Since the total length of the string is constant, x+2y+b={{l}_{0}}= constant.
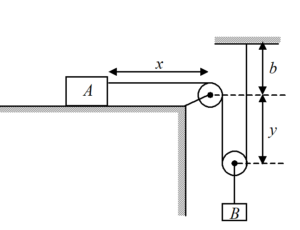
Here {{l}_{0}} is the total length of the string, which is a constant and b is also a constant.
\ x+2y= constant
On differentiating twice w.r.t. time, we get \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}+2\frac{{{{d}^{2}}y}}{{d{{t}^{2}}}}=0
Since x is decreasing and y is increasing with time, therefore
\frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}=-{{a}_{A}} and \frac{{{{d}^{2}}y}}{{d{{t}^{2}}}}={{a}_{B}}
\ -{{a}_{A}}+2{{a}_{B}}=0
or {{a}_{A}}=2{{a}_{B}}
Hence the acceleration of block A is twice that of B from constraint relation.
Illustration
Determine the accelerations of the masses in the pulley system shown in figure. Neglect the masses of the pulleys and string, and also friction. In what direction will the pulleys rotate when the masses move?
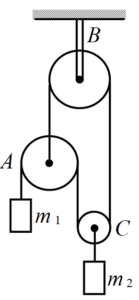
Solution
Since the masses of the pulleys and the string is negligibly small, the tension of the string is the same everywhere. Considering free-body diagrams of {{m}_{{1\,}}},\,{{m}_{2}} and the pulley A and applying Newton’s second law, we get
{{m}_{1}}g\,-\,T\,=\,{{m}_{1}}\,{{a}_{1}}
2T\,-\,{{m}_{2}}g\,=\,{{m}_{2}}{{a}_{2}}
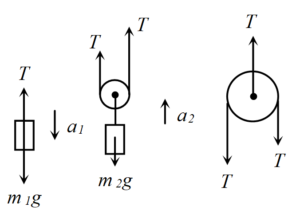
2T\,-\,T\,=\,0 since the mass of the pulley is zero
From the third equation we have T\,\,=\,\,0\,.
Substituting T\,=\,0 in the first two equations we have
{{a}_{1}}\,\,=\,\,{{a}_{2}}\,\,=\,g
Thus the weights fall freely, the pulleys B and C rotate counter clockwise and the pulley A clockwise.
Practice Questions (Basic Level)
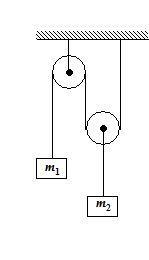
1.
For the system shown in the figure find the tension in the longer string. Take
m1 = m2 = 1 kg.
(a)2 N
(b) 6 N
(c) 10 N
(d) 20 N
Ans (b)
Comprehension Based Question (2 to 4)
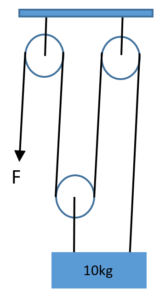
A 10 kg block is held by a pulley system as shown in the figure. What force F must be applied in the following cases:
2.
To hold the block at rest.
(a)10 N
(b) 30 N
(c)35 N
(d) 100/3 N
Ans (d)
3.
to lower it at 2 m/s.
(a) 5 N
(b) 25/3 N
(c) 100/3 N
(d) 50 N
Ans (c)
4.
to raise it with an acceleration of 2 m/s2 ?
(a) 47.25 N
(b) 45.50 N
(c) 40 N
(d) 20.38 N
Ans (c)
5.
The mechanical advantage of the system is
(a)2
(b)3
(c)4
(d)100/3
Ans (b)
6.
The mechanical advantage of the ideal pulley system shown in the figure given below is
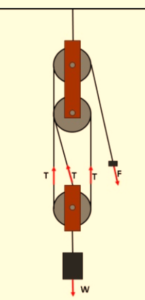
(a) 2
(b) 5
(c) 3
(d) 1
Ans. (c)
7.
W and F are two masses hanging in a pulley system as shown.
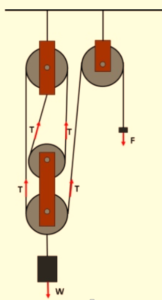
Choose the incorrect statement (assuming all pulley are ideal)
(a) If F = 20N and W = 80N, the system remains in equilibrium
(b) If F= 30N and W = 8kg then W will move downward
(c) If F=80 N and W= 3kg then W will move with an acceleration of \displaystyle 2.21m/{{s}^{2}}
(d) The mechanical advantage of the system is 4
Ans. (b)
Practice Questions (JEE Main Level)
1.
The figure shows a system of three masses such that m1¹m2¹m3. Find the relation between masses such that m3 remains stationary.
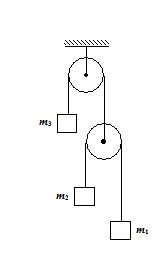
(a)\frac{4}{{{{m}_{3}}}} =\frac{1}{{{{m}_{1}}}}\,-\frac{1}{{{{m}_{2}}}}
(b)\frac{4}{{{{m}_{3}}}} =\frac{1}{{{{m}_{1}}}}\,+\frac{1}{{{{m}_{2}}}}
(c)\frac{4}{{{{m}_{3}}}} =\frac{1}{{{{m}_{2}}}}\,-\frac{1}{{{{m}_{1}}}}
(d)\frac{4}{{{{m}_{3}}}} =\frac{3}{{{{m}_{3}}}}\,+\frac{2}{{{{m}_{5}}}}
Ans (b)
Comprehension Based Question (2 and 4)
Consider the situation shown in the figure. Both the pulleys and the strings are light and all the surfaces are frictionless.
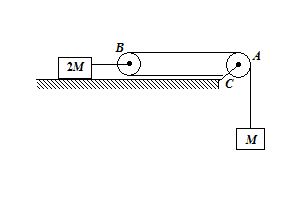
2.
Find the acceleration of the mass M
(a)\frac{2}{9}g
(b)\frac{2}{5}g
(c)\frac{2}{7}g
(d)\frac{2}{3}g
Ans (d)
3.
Find the tension in the string
(a)\frac{{mg}}{3}
(b)\frac{{mg}}{5}
(c)\frac{{2mg}}{3}
(d)\frac{{mg}}{{\sqrt{3}}}
Ans (a)
4.
Calculate the force exerted by the clamp C on the pulley A as shown in the figure.
(a)\frac{{\sqrt{5}}}{3}\,mg
(b)\frac{{\sqrt{2}}}{3}\,mg
(c)\frac{{\sqrt{2}}}{5}\,mg
(d)\frac{{\sqrt{2}}}{9}\,mg
Ans (b)
5.
A block is placed on a triangular wedge of inclination q as shown in the figure. Assuming friction is absent, if the acceleration of the wedge is a . Chose the correct option
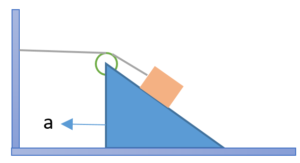
(a) the acceleration of the block is also a in the ground frame
(b) the acceleration of the block is a sinq in the ground frame
(c) the acceleration of the block is also a in the wedge frame
(d) both b and c options are correct
Ans : (d)
6.
A mass A is placed on a wedge B as shown in the figure. The wedge is given an acceleration a towards left. Assuming all surfaces are frictionless.
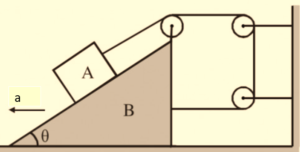
(i) The acceleration of mass A with respect to the wedge is
(a) \displaystyle 2a\sin \theta
(b) \displaystyle 2a
(c) \displaystyle a
(d) \displaystyle 2a\sin \frac{\theta }{2}
Ans : (b)
(II) The acceleration of mass A with respect to the ground is
(a) \displaystyle 2a\sin \theta
(b) \displaystyle 2a
(c) \displaystyle a
(d) \displaystyle a\sqrt{{1+8{{{\sin }}^{2}}\frac{\theta }{2}}}
Ans : (d)
7.
Two masses 1 and 2 are connected through a multi pulley system as shown in the figure. The mass 1 is of 2kg and the mass 2 is of 1kg. Their accelerations are shown in the figure.
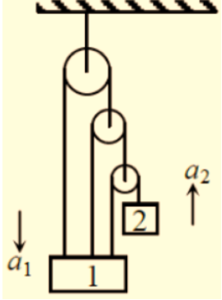
Choose the correct option
(a) \displaystyle {{a}_{1}}=-\frac{{350}}{{51}}m{{s}^{{-2}}}
(b) \displaystyle {{a}_{2}}=-\frac{{50}}{{51}}m{{s}^{{-2}}}
(c) \displaystyle {{a}_{2}}=-\frac{{350}}{{51}}m{{s}^{{-2}}}
(d) \displaystyle {{a}_{1}}=7{{a}_{2}}
Ans : (c)
8.
Two masses A and B are connected as shown and are moving on the horizontal frictionless surface. At the given instant A is moving leftward with a speed of 10m/s.
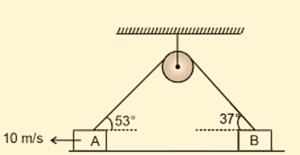
The speed of B with respect to A at this instant must be
(a) 10m/s
(b) 7.5m/s
(c) -7.5m/sec
(d) -2.5m/s
Ans : (d)
9.
Two masses A and B are connected as shown in the figure through multi pulley system.
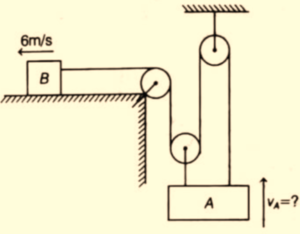
At the given instant the magnitude of velocity and its direction for mass B is shown in the figure. At this instant the relative velocity of mass B with respect to mass A is
(a) 2m/s upward
(b) \displaystyle 10\sqrt{2} m/s making an angle of \displaystyle {{45}^{o}}
(c) \displaystyle 2\sqrt{{10}} m/s making an angle \displaystyle {{\tan }^{{-1}}}\left( {\frac{1}{3}} \right) with x-axis in 3rd quadrant.
(d) \displaystyle 2\sqrt{{10}} m/s making an angle \displaystyle {{\tan }^{{-1}}}\left( {\frac{1}{3}} \right) with x-axis in 4th quadrant.
Ans.(c)
10.
Assuming all surfaces are frictionless.
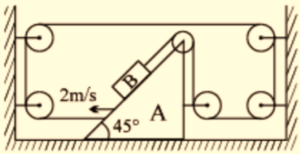
The velocity of mass B in the ground frame is
(a) \displaystyle -2\hat{i}\text{ m/s}
(b) \displaystyle 2\hat{i}-2\hat{j}\text{ m/s}
(c) \displaystyle -2\hat{i}\text{ + 2}\hat{j}\text{ m/s}
(d) \displaystyle 2\hat{i}\text{ m/s}
Ans. (a)
Practice Questions (JEE Advance Level)
1.
For the arrangement shown in the figure. When the system is released, find the acceleration of the wedge. The masses of the pulley and the thread are negligible. The friction is absent.
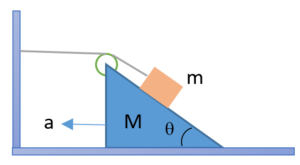
(a)\left[ {a\,=\frac{{mg\sin \theta }}{{M\,+\,2m\,(1\,-\,\cos \theta )}}} \right]
(b)\left[ {a\,=\frac{{mg\sin90}}{{M\,+\,3m\,(1\,-\,\cos \theta )}}} \right]
(c)\left[ {a\,=\frac{{mg\sin \theta }}{{M\,+\,5m\,(5\,-\,\cos \theta )}}} \right]
(d)\left[ {a\,=\frac{{mg\sin \theta }}{{M\,+\,m\,(1\,+\,\cos \theta )}}} \right]
Ans (a)
2.
The figure shows a rod of mass 2m restricted horizontally by two vertical supports rests on a wedge of mass m. When the rod is released from rest find the acceleration of the rod and that of the wedge. All surfaces are frictionless
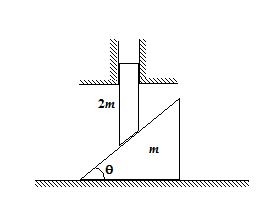
(a)arod=\frac{{g}}{{3\,+\,{{{\cot }}^{3}}\theta }};awedge =\frac{{2g}}{{2\tan \theta \,+\,\cot \theta }}
(b)arod=\frac{{3g}}{{2\,+\,{{{\cot }}^{2}}\theta }}; awedge =\frac{{g}}{{2\tan \theta \,+\,\cot \theta }}
(c)arod=\frac{{2g}}{{2\,+\,{{{\cot }}^{2}}\theta }};awedge=\frac{{2g}}{{2\tan \theta \,+\,\cot \theta }}
(d)arod=\frac{{g}}{{3\,+\,{{{\cot }}^{2}}\theta }}; awedge =\frac{{3g}}{{3\tan \theta \,+\,\cot \theta }}
Ans (c)
3.
In the arrangement shown in figure, the mass of ball 1 is equal to that of rod 2. The length of the latter is l = 10 cm. The masses of the pulleys and the threads, as well as the friction, are negligible. The ball is set on the same level as the lower end of the rod and then released. How soon will the ball be opposite to the upper end of the rod. ?
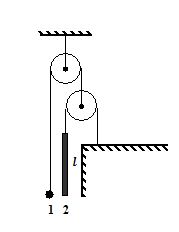
(a) 0.10 s
(b) 0.15 s
(c) 0.18 s
(d) 0.25 s
Ans (c)
4.
A sphere of mass m is placed on a movable wedge of mass 2m. At the center of the sphere a string is connected which passes over two frictionless pulleys one is fixed and the other is movable.The center of the movable pulley is connected to the center of another pulley over which a string passes and is connected to a hanging mass m.
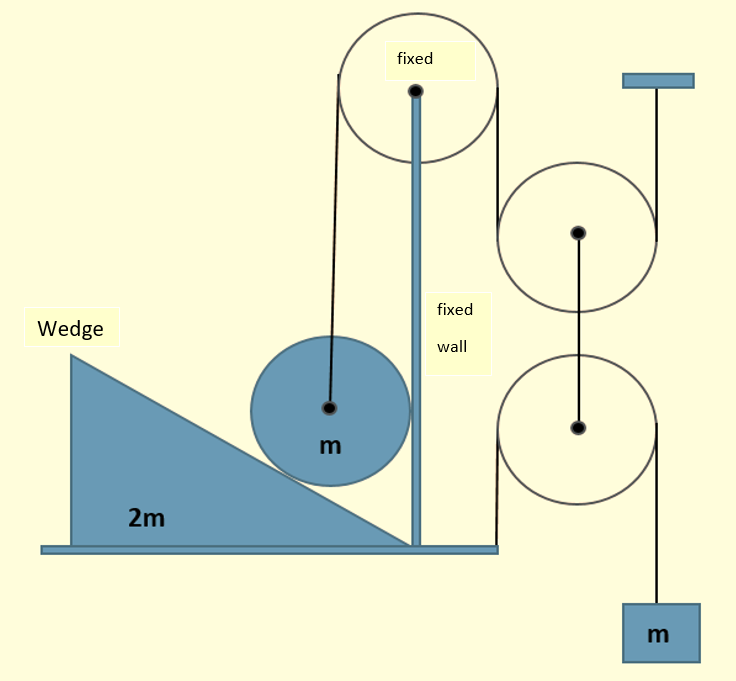
Assuming all surfaces are frictionless.If the acceleration of the hanging mass is a upward then
(a) The acceleration of the wedge is 2a/3 rightward
(b) The acceleration of the wedge is a/3 leftward
(c) The acceleration of the wedge is 4a/3 leftward
(d) The acceleration of the wedge is a leftward
Ans : (c)
5.
A sphere is placed on an inclined surface of angle \displaystyle \alpha . The sphere is touching the vertical edge of a triangular wedge placed on another inclined surface of angle \displaystyle \beta .
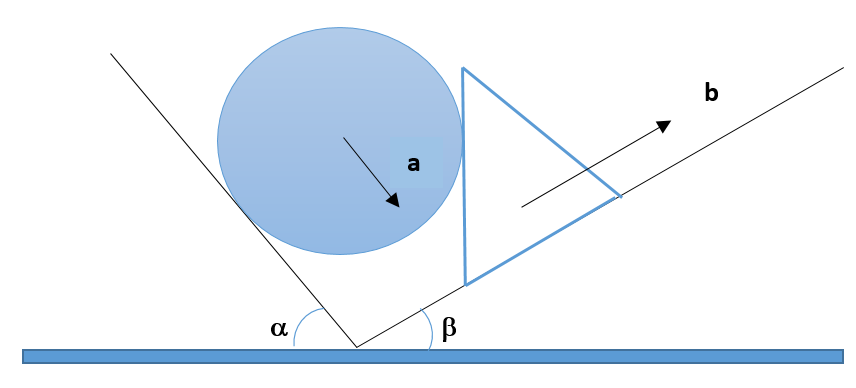
If the accelerations of the sphere and the wedge is a and b respectively as shown in the figure then
(a) \displaystyle a=\frac{{b\cos \beta }}{{\cos \alpha }}
(b) \displaystyle b=\frac{{a\cos \beta }}{{\cos \alpha }}
(c) \displaystyle a=\frac{{b\sin \beta }}{{\cos \alpha }}
(d) \displaystyle b=\frac{{a\sin \beta }}{{\sin \alpha }}
Ans : (a)
6.
The speed of the mass `E’ in the given system is
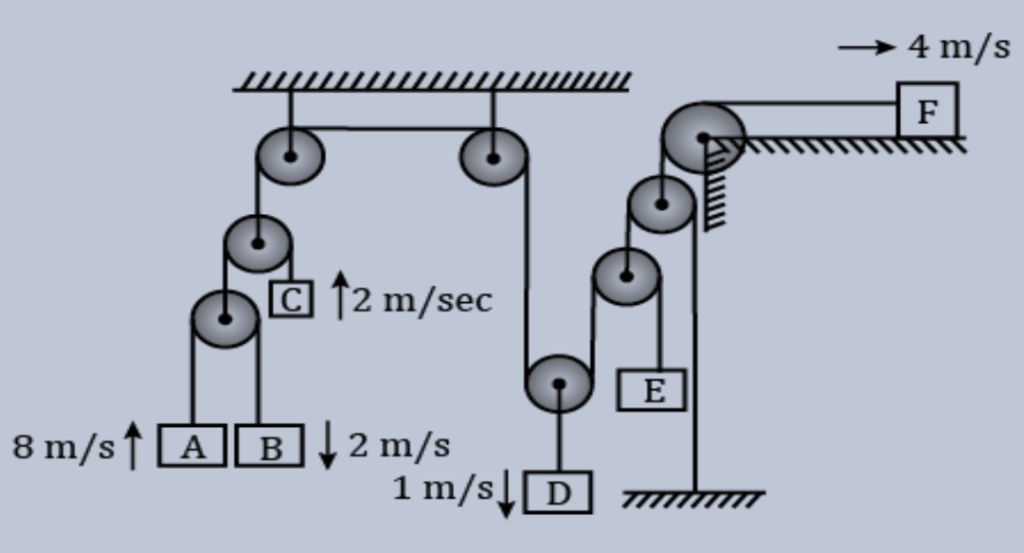
(a) 21/2 m/s
(b) 31/2 m/s
(c) 5 m/s
(d) 15 m/s
Ans. (b)
7.
A sphere is placed between two smooth wedges. At a certain instant the wedges are given velocity as shown in the figure.
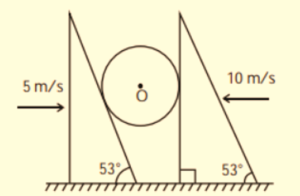
The velocity of the center of the sphere must be
(a) 20 m/s
(b) 15 m/s
(c) 5 m/s
(d) 10 m/s
Ans. (a)
8.
In the given system the wedge A moves towards right with a speed of 10m/s. The wedge B is moving down the inclined surfase with 5m/s relative to A.
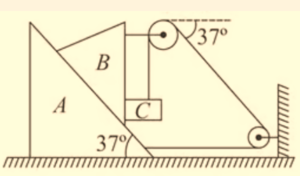
Assuming no friction anywhere, then the velocity vector of C must be
(a) \displaystyle -13\hat{j}\text{ m/s}
(b) \displaystyle 14\hat{i}-13\hat{j}\text{ m/s}
(c) \displaystyle 2\hat{i}\text{ – 2}\hat{j}\text{ m/s}
(d) \displaystyle 14\hat{i}\text{ m/s}
Ans. (b)

