Video Lecture
Theory For Notes Making
Newton’s Laws
Newton’s First Law
(a)
Everybody continues in its state of rest of uniform motion in a straight line unless it is compelled by a resultant force to change that state.
(b)
This law is also known as law of inertia.
(c)
Inertia is the property of inability of a body to change its position of rest or uniform motion in a straight line unless some external force acts on it.
(d)
Mass is a measure of inertia of a body.
(e)
A frame of reference in which Newton’s first law is valid is called inertia frame, i.e., if a frame of reference is at rest or in uniform motion it is called inertial, otherwise non-inertial.
Newton’s Second Law
The rate of change of momentum is directly proportional to the net external force and takes place in the direction of the force.
\displaystyle \vec{F}\,=\,\frac{{d\vec{p}}}{{dt}}\,=\,\frac{{md\vec{v}}}{{dt}}\,=\,m\vec{a}
The net external force acting on a particle produces acceleration. The magnitude of the acceleration produced depends on the quantity of matter being acted upon. The quantity of matter is referred to as the mass. The direction of acceleration is the direction of the net external force.
So mathematically,
Fnet = ma,
Fnet includes sum of all external forces.
\displaystyle F\,=\,m\left( {\frac{{d{{v}_{x}}}}{{dt}}\hat{i}+\frac{{d{{v}_{y}}}}{{dt}}\hat{j}\,+\,\frac{{d{{v}_{z}}}}{{dt}}\hat{k}} \right)
\displaystyle {{F}_{x}}\hat{i}+{{F}_{y}}\hat{j}+{{F}_{z}}\hat{k}=m\frac{{d{{v}_{x}}}}{{dt}}\hat{i}+m\frac{{d{{v}_{y}}}}{{dt}}\hat{j}+m\frac{{d{{v}_{z}}}}{{dt}}\hat{k}
\displaystyle {{F}_{x}}\,=\,m\frac{{d{{v}_{x}}}}{{dt}}
\displaystyle {{F}_{y}}=m\frac{{d{{v}_{y}}}}{{dt}}, \displaystyle {{F}_{z}}=m\frac{{d{{v}_{z}}}}{{dt}} [component Form]
\displaystyle {{a}_{x}}=\frac{{{{F}_{x}}}}{m}, \displaystyle {{a}_{y}}=\frac{{{{F}_{y}}}}{m}, \displaystyle {{a}_{z}}=\frac{{{{F}_{z}}}}{m}
Newton’s Third Law
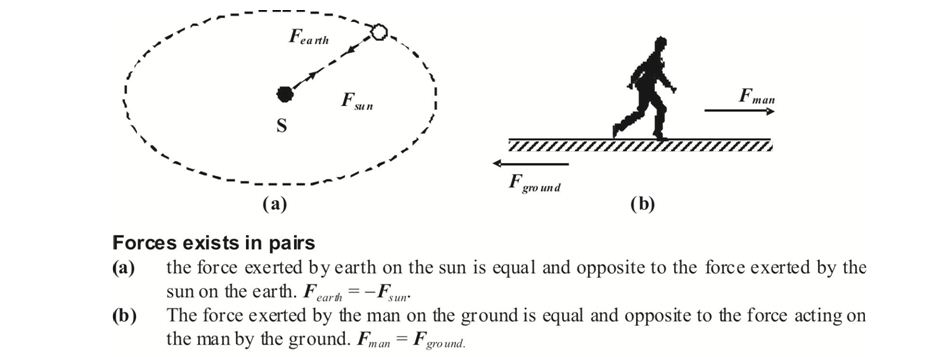
To every action (Force) there is an equal and opposite reaction (Force). Forces always occur in pair. Force is the result of mutual interaction between two bodies. Mutual forces between two bodies are always equal and opposite.
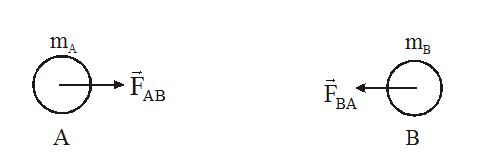
Let body B exerts force \displaystyle {{a}_{z}}=\frac{{{{F}_{z}}}}{m} on body A, body A exerts a force \displaystyle {{\vec{F}}_{{BA}}} on body B. These forces are related by \displaystyle {{\vec{F}}_{{AB}}}=-{{\vec{F}}_{{BA}}}
The negative sign represents opposite direction. The two forces involved in any interaction between two bodies are called action and reaction. But we cannot say that this particular force is action and the other one is reaction. Action and Reaction always acts on different bodies.
If the object exerts a force F on a second, then the second object exerts an equal but oppositely force –F on the first
Illustration
An object of 5 kg is far away from the surface of the earth and has an acceleration of 6 m/s^2 towards the center of earth. Find the force exerted by the object on the earth.
Solution
Force on object by the earth, \displaystyle {{\vec{F}}_{{OE}}}={{m}_{{ob}}}.{{\vec{a}}_{{ob}}}=(5\times 6)N=30N
Force between earth and object makes an action reaction pair thus force exerted by object on earth is also 30 N directed away for the center of earth.
Illustration
The momentum of a block is given by \displaystyle P=(10{{t}^{2}}\hat{i}+5t\hat{j}) kg m/s. Find the force acting on block at t = 2 s.
Solution
\displaystyle F=\frac{{dP}}{{dt}}=\frac{d}{{dt}}(10{{t}^{2}}\hat{i}+5t\ \hat{j})=20t\hat{i}+5\ \hat{j}
At t = 2 s, \displaystyle F=(40\hat{i}+5\hat{j})\ \ N
Illustration
A body of mass 6 kg moves in a straight line according to the equation
x = t3 – 75t
where x denotes the distance in metre and t the time in second. The force on the body at t = 4 second is
(a) 64 newton (b) 72 newton (c) 144 newton (d) 36 newton
Solution
x = t3 – 75 t
\displaystyle v=\frac{{dx}}{{dt}}=3{{t}^{2}}-75
\displaystyle a=\frac{{dv}}{{dt}}=6t
t = 45; a = 24 ms– 2
F = ma = 6 × 24 = 144 N Ans. (c)
Basic force in nature
(i)
There are four types of basic forces that exist in nature :
(a) Gravitational force
(b) Electromagnetic force
(c) Nuclear force
(d) Weak force
(ii)
Many other well known forces like frictional force, elastic force, viscous force, spring force, intermolecular force are manifestations of electromagnetic forces.
(iii)
The gravitational and the electromagnetic forces are long range forces having infinite range while nuclear and weak forces are very short range forces.
(iv)
The nuclear force is the strongest force while the gravitational force is the weakest force of nature. Electromagnetic force is about 1036 times stronger than gravitational force while weak forces are about 1025 times as strong as gravitational force. The relative magnitudes of different forces can be expressed as :
(v)
\displaystyle {{F}_{G}}:\,{{F}_{W}}:{{F}_{E}}:{{F}_{N}}\,::1:{{10}^{{25}}}:{{10}^{{36}}}:{{10}^{{38}}}
i.e., \displaystyle {{F}_{N}}>\,\,{{F}_{E}}>{{F}_{W}}>{{F}_{G}}
(vi)
Gravitational and electromagnetic forces are central or conservative forces and obey inverse square law, while nuclear force is a non-central force and varies inversely with some higher power of distance.
(vii)
There are certain reactions like beta-decay, which can be explained only on the basis of weak forces.
(viii)
Electromagnetic interactions can be explained on the basis of exchange of photons; gravitational force on the basis of exchange of gravitation; weak forces on the basis of exchange of \displaystyle {{W}^{+}},\,\,{{W}^{-}},\,\,{{Z}^{0}} bosons and nuclear forces on the basis of exchange of \displaystyle \pi -mesons.
Force
We know by experience that all bodies in nature interact in some way with one another. Force is a measure of the interaction between the bodies. The force may either produce deformation (change in the size or shape of bodies) or acceleration (change in magnitude or direction of their velocity).
It can be described as a push or a pull. The pull is always oriented away from the body; and the push is always oriented towards the body.

Force is a vector quantity. Every force has a definite direction and the result of its action depends on the direction and the magnitude of the force.If several forces are applied to a particle, they can be replaced by the resultant force.
Units of force
Absolute units : (i) Newton (S.I.) (ii) Dyne (C.G.S)
Gravitational units : (i) Kilogram-force (M.K.S.) (ii) Gram-force (C.G.S)
Newton : One Newton is that force which produces an acceleration of 1\,m/{{s}^{2}} in a body of mass 1 Kilogram.
\therefore 1 Newton =1kg-\,m/{{s}^{2}}
Dyne : One dyne is that force which produces an acceleration of 1cm/{{s}^{2}} in a body of mass 1 gram.
1 Dyne =1gm\,cm/{{\sec }^{2}}
Relation between absolute units of force 1Newton ={{10}^{5}} Dyne
Kilogram-force :It is that force which produces an acceleration of 9.8m/{{s}^{2}} in a body of mass 1 kg.
1 kg-f = 9.80 Newton
Gram-force : It is that force which produces an acceleration of \displaystyle 980cm/{{s}^{2}} in a body of mass 1gm.
1 gm-f = 980 Dyne
Free body Diagram
In mechanics, diagram of an isolated body along with forces acting on it is very useful in the analysis of mechanical problems. Such diagram is defined as free-body diagram.
Some Common Forces
There are, basically, five forces which we commonly encounter in mechanics, namely the weight, the normal forces, the friction force, the tension, the spring force
Weight
Weight is the force with which the earth attracts every other body. It is also called the force of gravity or the gravitational force. If they do not fall to the earth, then their motion is restricted by certain other bodies : a support, string, spring, etc. Bodies that restrict the motion of other bodies are called constraints. These bodies restrict the motion of the given bodies. For example, the surface of the table is the constraint for all objects lying on it, the floor serves as the constraint for the table, etc.

Normal force
It is the reaction force provided by the surface in contact with the body against the component of force by which body press the surface.
It is a self-adjusting force act on the body in a direction normal to the surface through the points of contacts and with a pushing tendency that is never being achieved by it.
Normal reaction is not a basic fundamental force rather it arises due to the electromagnetic interaction between the atoms of body and of surface which are in contact with each other. Its magnitude can be calculated using Newton’s Law of motions as follows:
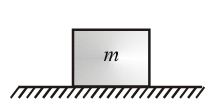
Consider a block of mass m placed at rest on the horizontal surface may be smooth or rough as shown in figure. The block experience two external forces:
- One is the weight mg arises due to the gravitational interaction with earth.
- Second force N arises due to the interaction of block with surface called normal reaction as shown in the F.B.D. of block with respect to ground observer.
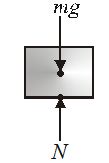
As the acceleration of the block is zero in the frame of reference of ground observer, the second law of motion suggest that
N-mg=0 …. (i)
or N=mg
Thus the force exerted by ground on the block is equal to the weight of block itself. Further force exerted by block on the ground is N in downward direction too as suggested by Newton’s third law. Hence, the normal reaction exerted by the ground is equal and opposite to the force exerted by block on ground which is equal to the weight of the block in this situation.
If the surface is accelerating upward with an acceleration a then, in the reference of the observer on the ground, the equation (i) modified as
N-mg=ma
N=m(g+a) …. (ii)
Thus, the normal reaction by the ground on block is increase by an amount ma. It is obvious because now the surface not only holding a block to fall down but also giving it an upward push to accelerate upward.
The normal reaction provided by surface to stationary block in three commonly encountered situations as shown in figure, is given as:
A block of mass m placed on ground and is pulled with a force F inclined at an angle \theta with horizontal.
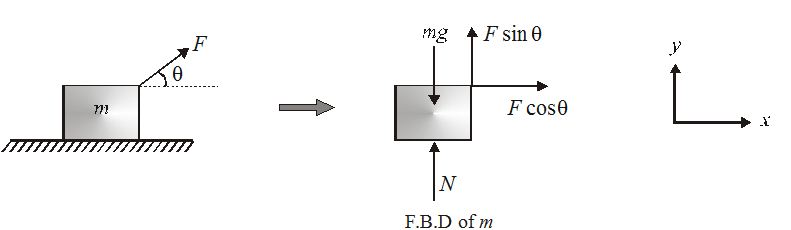
From the Newton’s Laws, the equation in Y-direction gives
N-mg+F\sin \theta =0
or N=mg-F\sin \theta
Similarly, if the block is pushed by force F, at an angle \theta with horizon, then
N=mg+F\sin \theta
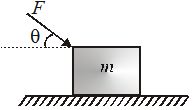
A block of mass m placed on an inclined ground of inclination \theta .
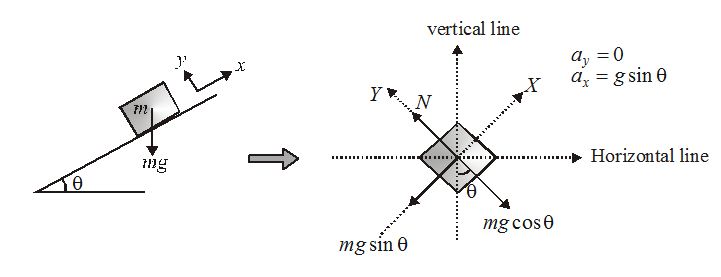
The equation of motion in Y–axis gives
mg\cos \theta -N=0 or N=mg\cos \theta
- A block of mass m is pushed against a vertical wall by force F
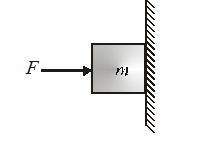
The equation of motion in X-direction gives
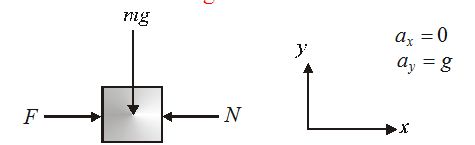
F-N=0 or N=F
Note that the normal force does not depend on the weight of body but generally a part of weight press surface, so N contains a term of weight.
Frictional Forces
The component of the contact force parallel to the contact surface is called the frictional force. The direction of the frictional force is opposite to the relative motion (or attempted motion) of the two surfaces in contact.
Spring Force
When a spring is deformed(stretched or compressed), it resists the deformation by generating a force called the spring force.
The magnitude of spring force {{F}_{s}} is proportional to the deformation as
{{F}_{s}}=kx
Where k is called the stiffness constant or spring constant. In the vector form, it may be written as
{{\vec{F}}_{s}}=-k\vec{x}
The negative sign indicates that the spring force is always opposite to the direction of deformation.
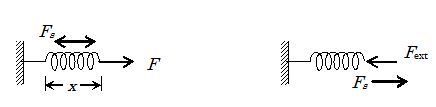
Fext = external force applied on the force, FS = spring force resisting the deformation
Internal and External force :
The forces of interaction between portions of a system of bodies being considered are called internal forces. The force exerted on bodies of a given system by bodies not included in this system are called external forces. A system of bodies on each of which no external forces act is called a closed (isolated) system.
Tension
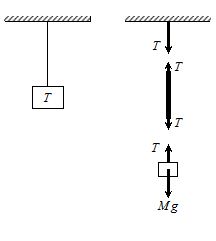
The force exerted by the end of a taut string, rope or wire is called the tension. The direction of this force is such that the string pulls the object to which it is attached. It is difficult to push with a string
Illustrations
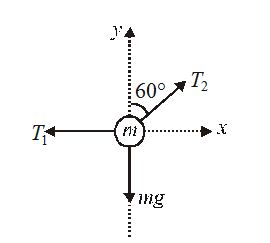
A ball of mass m=5\,\,\mathbf{kg} is suspended with two strings as shown in figure.
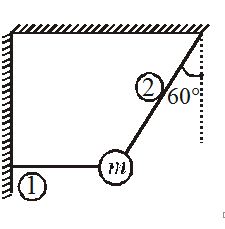
Solution: The F.B.D of the ball is shown in figure.
Illustration
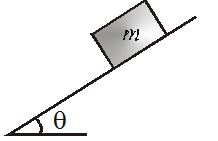
A block of mass m is placed on a rough inclined surface of inclination \theta as shown in figure.Draw the F.B.D. of block
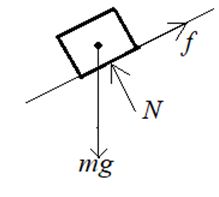
Solution
The F.B.D. of the block is, shown in figure, with N as the normal reaction and f is the friction force.
Equilibrium of Concurrent Force
(1)
If all the forces working on a body are acting on the same point, then they are said to be concurrent.
(2)
A body, under the action of concurrent forces, is said to be in equilibrium, when there is no change in the state of rest or of uniform motion along a straight line.
(3)
The necessary condition for the equilibrium of a body under the action of concurrent forces is that the vector sum of all the forces acting on the body must be zero.
(4)+
Mathematically for equilibrium ∑Fnet = 0 or \sum{{{{F}_{x}}=0}}; \sum{{{{F}_{y}}=0}}; , \sum{{{{F}_{z}}=0}}
(5)
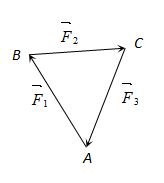
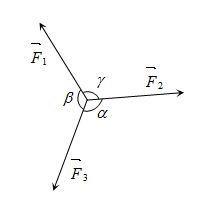
Three concurrent forces will be in equilibrium, if they can be represented completely by three sides of a triangle taken in order.
(6) Lami’sTheorem : For three concurrent forces in equilibrium
\frac{{{{F}_{1}}}}{{\sin \alpha }}=\frac{{{{F}_{2}}}}{{\sin \beta }}=\frac{{{{F}_{3}}}}{{\sin \gamma }}
Illustration
A block A is kept stationary on a wedge B by applying a force F as shown in figure.
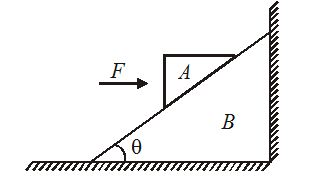
(a)Draw the F.B.D. of the block.
(b) Determine the normal reaction exerted on block by the wedge.
(c) If mass of the block is m, then determine the minimum value of F required keeping the block A stationary.
Assume that there is no friction anywhere in the system.
Solution:
(a) The F.B.D. of block A is shown in figure.
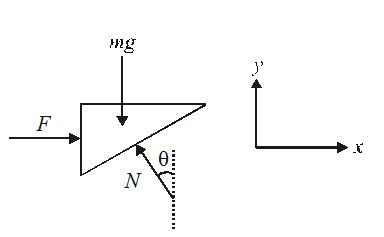
(b) The equations of motion of block are:
Along X-axis
F-N\sin \theta =m{{a}_{x}}and {{a}_{x}}=0
F=\mathbf{N}\sin \theta …(i)
Along Y-axis
N\cos \theta -mg=m{{a}_{y}}and {{a}_{y}}=0
N\cos \theta =mg …(ii)
Thus the normal reaction exerted on block by the wedge is
N=F/Sinθ … (iii)
(c) Dividing equation (i) by (ii), we get
F=mg tanθ …….(iv)
Illustration
Two blocks A and B, of masses 2.9 kg and 1.9 kg respectively, are suspended from a rigid support by inextensible strings. The length of each string is one metre and the upper string has negligible mass while the lower string has a uniform mass of 0.2 kg. Determine the tension at the mid points of strings when the support is
(a) stationary
(b) accelerating upward at the rate of \mathbf{0}\mathbf{.2}\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}}
(c) accelerating downward at the rate of \mathbf{0}\mathbf{.2}\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}}
Solution:
The problem can be solved by assuming that block A has mass (2.9+0.1)kg and block B has mass (0.9+0.1) kg and both the blocks are now connected with a massless string. The tension in the string connecting A and B is now same at each point and its value is equal to the tension at the mid point of a massive rope of mass 0.2 kg.
(a) When the support is stationary, then the tension in lower string balance the weight of block B and the tension in upper string balance the weight of both blocks A and B. Thus,
{{T}_{{lower}}}={{m}_{B}}g=2g=19.6\,\mathbf{N}
and {{T}_{{upper}}}=({{m}_{B}}+{{m}_{A}})g=(2+3)g=49\mathbf{N}
(b) When the support is acceleration upward, then, in the frame of reference of support, the system is in equilibrium due to the downward pseudo force, which increases the effective value of g by \mathbf{0}\mathbf{.2}\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}}.
Thus, the effective value of g is
{{g}_{{eff}}}=9.8+0.2=10\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}}
Now, the tension in strings is
{{T}_{{lower}}}={{m}_{B}}{{g}_{{eff}}}=2\times 10=20\mathbf{N}
and {{T}_{{upper}}}=({{m}_{B}}+{{m}_{A}}){{g}_{{off}}}=5\times 10=50\mathbf{N}
(c) When the support is acceleration downward, the effective value of g decreases by an amount of \mathbf{0}\mathbf{.2}\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}}.
Now, {{g}_{{eff}}}=9.8-0.2=9.6\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}}
and {{T}_{{lower}}}=2\times 9.6=19.2\,\mathbf{N}
{{T}_{{upper}}}=5\times 9.6=48.0\,\mathbf{N}
Illustration
A block of mass 25kg is raised by a 50 kg man in two different ways as shown in figure.
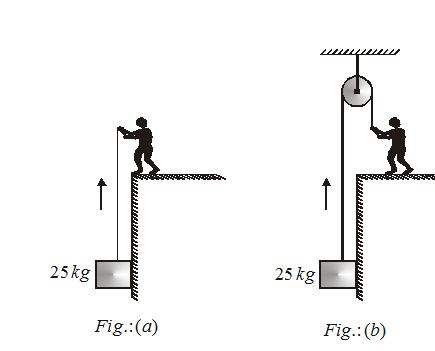
(a) What is the action on the floor by man in the two cases?
(b) If floor yields to a normal force of 700 N, which mode should the man adopt to lift block without the floor yield?
Solution:
(a) To raise the 25kg block upward, tension T required in the string is 25g. If N is the normal reaction exerted by floor on man, then the F. B.D. of man in two situations become as:
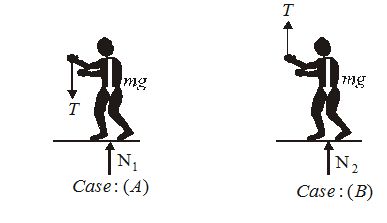
For case (A):
T+mg={{N}_{1}}
or {{N}_{1}}=25g+50g=75g=750\,\mathbf{N}
For case (B)
{{N}_{2}}=mg-T
or {{N}_{2}}=50g-25g=25g=250\mathbf{N}
Since {{N}_{1}}>700\,\mathbf{N}and {{N}_{2}}<700\,\mathbf{N}, so mode (B) should be adopted by the man to lift up block without getting yield the floor.
Objective Assignment
1.
A homogeneous rod of length L is acted upon by two forces F1 and F2 applied to its ends and directed opposite to each other. Find the magnitude of the pulling force F at a distance l from the end where F1 is applied.
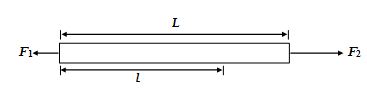
(a)\frac{{\left( {{{F}_{3}}-{{F}_{1}}} \right)l}}{L}+{{F}_{2}}
(b)\frac{{\left( {{{F}_{5}}-{{F}_{1}}} \right)l}}{L}+{{F}_{5}}
(c)\frac{{\left( {{{F}_{2}}-{{F}_{1}}} \right)l}}{L}+{{F}_{1}}
(d)\frac{{\left( {{{F}_{3}}-{{F}_{1}}} \right)l}}{L}+{{F}_{1}}
Ans (c)
Comprehension Based Question ( 2 and 3)
A particle of mass 10-2 g is moving along the positive x-axis under the influence of a force F(x) = -\frac{k}{{2{{x}^{2}}}} where k = 10-2 Nm2. At time t = 0 it is at x = 1.0 m and its velocity is v = 0
2.
Find its velocity when it reaches x = 0.5 m.
(a)1.0 m/s
(b)-1.0 m/s
(c)5.0 m/s
(d)-2.0 m/s
Ans (b)
3.
Find the time at which it reaches x = 0.25 m.
(a)t = 1.50 s
(b)t = 1.48 s
(c)t = 1.00 s
(d)t = 1.20 s
Ans (b)
4.
Figure shows the position–time graph of a particle of mass 4 kg. What is the
force on the particle for t< 0, t> 4s,
0 <t< 4s?
(Consider one–dimensional motion only)
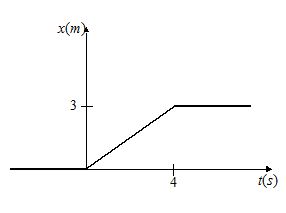
Ans – In all the three intervals, acceleration and, therefore, force are zero.
Comprehension Based Question (5 to 8)
A man of mass 70 kg stands on a weighing scale in a lift which is moving. What would be the readings on the scale in each case?
5.
Upwards with a uniform speed of 10 ms–1,
(a)N = 50 X 10 = 500 N; Reading is 50 kg
(b)N = 70 X 10 = 700 N; Reading is 70 kg
(c) N = 20 X 10 = 200 N; Reading is 20 kg
(d)N = 1 X 10 = 10 N; Reading is 1 kg
Ans (b)
6.
Downwards with a uniform acceleration of 5 ms–2,
(a)70 – 10 – N = 70 – 5; Reading is 35 kg
(b)70 – 50 – N = 70 – 9; Reading is 22 kg
(c)70 – 20 – N = 70 – 7; Reading is 30 kg
(d)70 – 10 – N = 70 – 2; Reading is 25 kg
Ans (a)
7.
Upwards with a uniform acceleration of 5 ms–2.
(a) N – 70 – 5 = 70 + 5; Reading is 100 kg
(b)N – 70 – 5 = 70 – 20; Reading is 20 kg
(c)N – 70 – 10 = 70 – 5; Reading is 105 kg
(d)N – 70 – 8 = 70 – 2; Reading is 10 kg
Ans (c)
8.
What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
(a)70 – 10 – N = 70 – 10; Reading would be zero
(b)70 – 10 – N = 70 – 10; Reading would be 70
(c)70 – 10 – N = 70 – 10; Reading would be 30
(d) 70 – 10 – N = 70 – 10; Reading would be 22
Ans (a)
9.
A horizontal force of 600 N pulls two masses 10 kg and 20 kg (lying on a frictionless table) connected by a light string. What is the tension in the string? Does the answer depend on which mass end the pull is applied?
(a) a = 20 ms–2, T = 400 N.
(b) a = 20 ms–2, T = 100 N.
(c) a = 20 ms–2, T = 200 N.
(d) a = 20 ms–2, T = 350 N.
Ans (a)
Comprehension Based Question (10 and 11 )
For the arrangement shown in the figure.
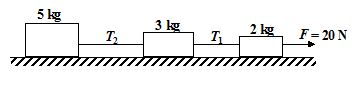
10.
Find the acceleration of each block.
(a) 2 m/s2
(b) 8 m/s2
(c)12 m/s2
(d) 10 m/s2
Ans (a)
11.
Find the tension in each string.
(a) T1 = 2 N; T2 =1 N
(b) T1 = 15 N; T2 =5 N
(c) T1 = 16 N; T2 =10 N
(d) T1 = 20 N; T2 =15 N
Ans (c)
Comprehension Based Question (12 and 13)
Two blocks are connected by a massless rope as shown. The horizontal surface is frictionless. If m1 = 2 kg, for what value of m2 will
12.
the acceleration of the system be 4 m/s2 and
(a) 1 kg
(b) 8 kg
(c) 5 kg
(d) 3 kg
Ans (d)
13.
the tension in the rope be 8 N ?
(a) (4/3) kg
(b) (5/3) kg
(c) (8/3) kg
(d) (2/3) kg
Ans (a)
14.
Calculate the tension in the string shown in figure. The pulleys and the string are light and all the surfaces are frictionless. Take g = 10 m/s2.
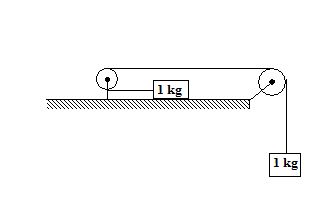
(a) 5 N
(b)10 N
(c) 15 N
(d) 50 N
Ans (a)
Comprehension Based Question (15 and 19)
Two blocks with masses m1 = 0.2 kg and m2 = 0.3 kg hang one under the other, as shown in the figure. Find the tensions in the (massless) strings in the following situations:
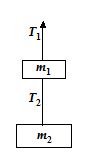
15.
The blocks are at rest.
(a) 2 N; 3 N
(b) 9 N; 8 N
(c) 7 N; 3 N
(d) 5 N; 3 N
Ans (d)
16.
They move upward at 5 m/s.
(a) 2 N; 3 N
(b) 9 N; 8 N
(c) 5 N; 3 N
(d) 7 N; 3 N
Ans(c)
17.
They accelerate upward at 2 m/s2.
(a) 2 N; 0.4 N
(b) 6 N; 3.6 N
(c) 7 N; 4.9 N
(d) 10 N; 10.0 N
Ans (b)
18.
They accelerate downward at 2 m/s2.
(a) 4 N, 2.4 N
(b) 4 N, 2.0 N
(c) 4 N, 2.8 N
(d) 4 N, 3.6 N
Ans (a)
19.
If the maximum allowable tension is 10 N, what is the maximum possible upward acceleration?
(a)5 m/s2
(b)10 m/s2
(c)25 m/s2
(d)30 m/s2
Ans (b)
Comprehension Based Question (20 to 22)
A person of mass 75 kg stands on a scale in an elevator. What can you infer about the motion if the scale reads :
20.
750 N
(a)v = constant
(b)v = 5
(c)v = 10
(d)v = 100
Ans (a)
21.
600 N
(a)5 m/s2 downward
(b)2 m/s2Upward
(c)3 m/s2 downward
(d)2 m/s2 downward
Ans (d)
22.
900 N
(a)2.8 m/s2 upward
(b)5.0 m/s2 upward
(c)2.0 m/s2 upward
(d)2.0 m/s2 downward
Ans (c)
23
A block of mass 25 kg is raised by a 50 kg man in two different ways as shown in figure. What is the action on the floor by the man in the two cases? If the floor yields to a normal force of 700 N, which mode should the man adopt to lift the block without the floor yielding?
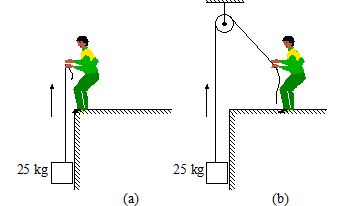
(a) Mode (a) Should Be Adopted
(b) Mode (b) Should Be Adopted
(c) Either Of (a) or (b) Should Be Adopted
(d) Neither (a) Nor (b) Should Be Adopted
Ans (b)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.




