Video Lecture
Theory For Notes Making
Introduction
When object is in Non-Uniform Motion or In a variable motion, the object will cover unequal distance in equal intervals of time.
The position-time graph of non uniform (varying) motion will not be a straight line.
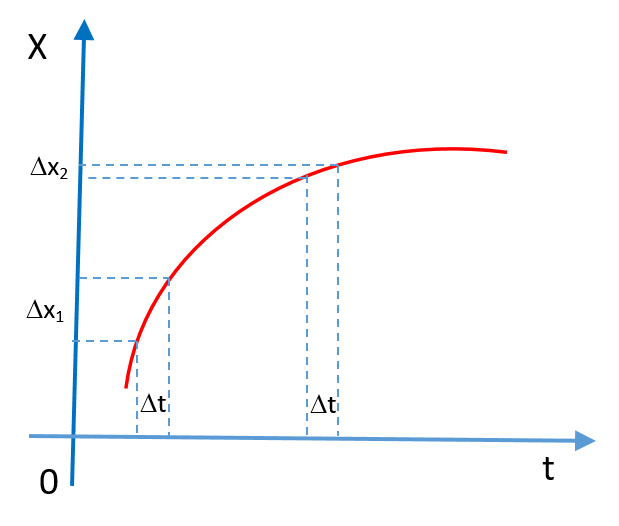
From the graph, it is clear that, object covers unequal distance in equal interval of time. Initially, in time Dt it covers a distance (Dx1) and after that it covers distance (Dx2) but in same time interval (Dt).
Average Acceleration and Instantaneous Acceleration
Very often, the velocity of a particle changes either in magnitude, in direction, or both as the motion proceeds. The body is then said to have an acceleration. The acceleration is defined as the time rate of change of velocity. The average acceleration is defined as
\vec{a}=\frac{{{{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}}}}{{{{t}_{1}}-{{t}_{1}}}}=\frac{{\Delta \vec{v}}}{{\Delta t}}
The direction of average acceleration (vector) is the direction of change in velocity (vector). Its unit is m/s2.
The instantaneous acceleration is defined by
\vec{a}=\underset{{\Delta t\to 0}}{\mathop {Lt}}\,\frac{{\Delta \vec{v}}}{{\Delta t}}=\frac{{d\vec{v}}}{{dt}}
In general, there is no relation between the direction of velocity vector and the direction of acceleration vector.
Graphical Analysis of Acceleration
Average Acceleration
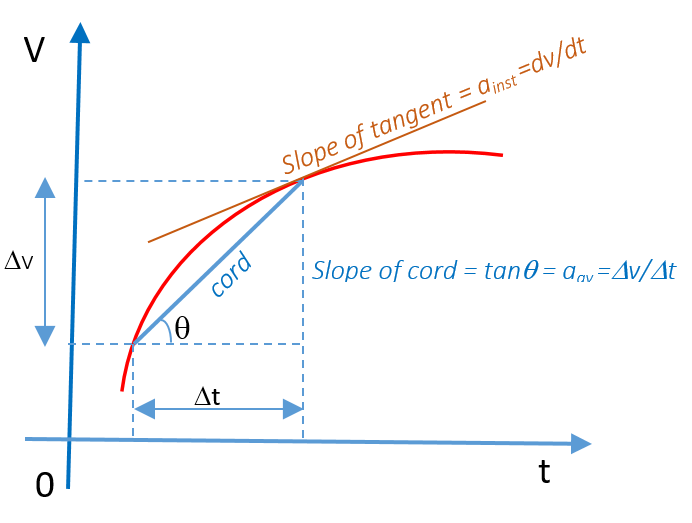
The average acceleration between two points in a time interval is equal to the slope of the chord connecting the points on a velocity-versus-time graph.
Instantaneous Acceleration
The instantaneous acceleration at time t is the slope of the tangent drawn to the velocity-versus-time graph as shown below.The sign of the instantaneous acceleration depends on the slope of the tangent.In the diagram given below the slope is positive hence the acceleration is also positive.
Non-Uniform Motion with Uniform Acceleration
In this section, we are going to derive relations among displacement, velocity, acceleration and time.
1st Equation of Motion
We know that, \frac{{dv}}{{dt}}\,=a
dv= adt
On integrating both sides,we get
\displaystyle \int\limits_{u}^{v}{{dv}}\,\,=\,\,a\int\limits_{0}^{t}{{dt}}
v = u + at … (1)
IInd Equation of Uniformly accelerated motion
Also we know that
\displaystyle \frac{{dx}}{{dt}}\,=\,v\,=\,u+\,at
or dx = (u + at)dt
On integrating, we get
\displaystyle \int\limits_{{{{x}_{0}}}}^{x}{{dx}}\,\,=\,\,u\int\limits_{0}^{t}{{dt\,+\,a\int\limits_{0}^{t}{{tdt}}}}
x = x0 + ut + \displaystyle \frac{1}{2}at2 … (2)
The equation (2) may be rewritten as
\displaystyle x={{x}_{0}}+t\left( {u+\frac{{at}}{2}} \right)
From equation (1), we have
x={{x}_{{0}}}+t(u+\frac{{v-u}}{2})
thus \displaystyle x={{x}_{0}}+\frac{1}{2}(u+v)t … (4)
IIIrd Equation of Uniformly accelerated motion
Eliminating t from equations (1) and (2), we get
v2 = \displaystyle u_{{}}^{2}\,+\,2a\,(x\,-\,{{x}_{0}}) … (3)
All these equations are called the equations of kinematics in one dimensional motion
The equations of kinematics are summarized as
v= u + at (1)
x = x0+ ut+ \displaystyle \frac{1}{2}\,a{{t}^{2}} (2)
\displaystyle {{v}^{2}}\,=\,u_{{}}^{2}\,+2a\,(x\,-\,{{x}_{0}}) (3)
x = x0 + \displaystyle \frac{1}{2} (u + v)t (4)
wherex0= initial position coordinate; x = Final position coordinate
v= final velocity; a = acceleration (constant)
t = time elapsed
Displacement of the particle in nth Second
Let an object is moving with initial velocity u under constant acceleration a.
To find the displacement in nth second, we subtract the position of particle at (n –1)th second from the position of the particle at nth second.
Displacement in nth second = \displaystyle {{s}_{n}}-{{s}_{{n-1}}}
\displaystyle s\left( {nth} \right)=un+\frac{1}{2}a\left( {{{n}^{2}}} \right)-\left[ {u\left( {n-1} \right)+\frac{1}{2}a{{{\left( {n-1} \right)}}^{2}}} \right]
\displaystyle =un\,+\,\frac{1}{2}a{{n}^{2}}-un+u-\frac{1}{2}a{{\left( {n-1} \right)}^{2}}
\displaystyle =u\,+\,\frac{a}{2}\,\left[ {{{n}^{2}}-{{{\left( {n-1} \right)}}^{2}}} \right] \displaystyle =u\,+\,\frac{a}{2}\,\left( {{{n}^{2}}-{{n}^{2}}-1+2n} \right)
Displacement in the nth second, \displaystyle s\left( {nth} \right)\,=\,u\,+\,\frac{a}{2}\left( {2n-1} \right)
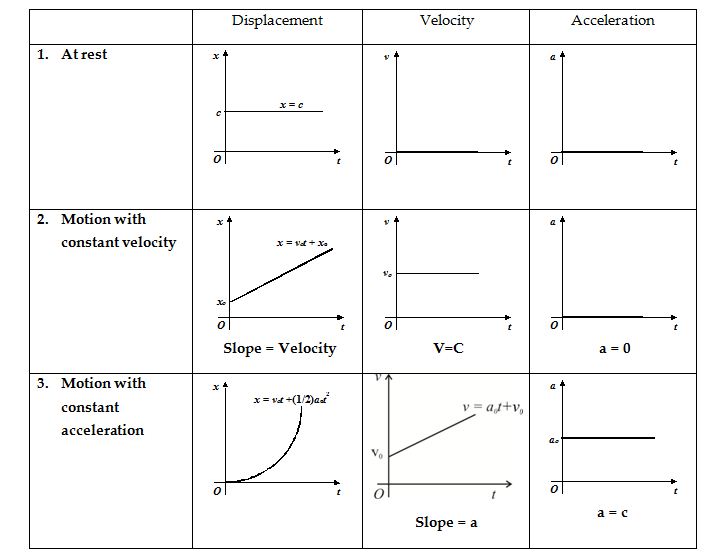
Variation of Displacement (x), velocity (v) and acceleration (a) with respect to time for different types of motion.
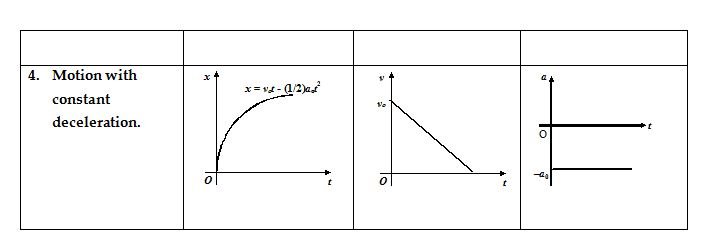
Points to remember :
1. The slope of displacement –time graph or position – time graph gives velocity.
2. The slope of velocity – time graph gives acceleration.
3. The area under velocity-time graph gives displacement.
Illustration
The figure shows the x-t plot of a particle in 3-dimensional motion. Three different equal intervals of time are shown. In which interval the average speed is greatest and in which it is the least ? Give the sign of average speed for each interval.
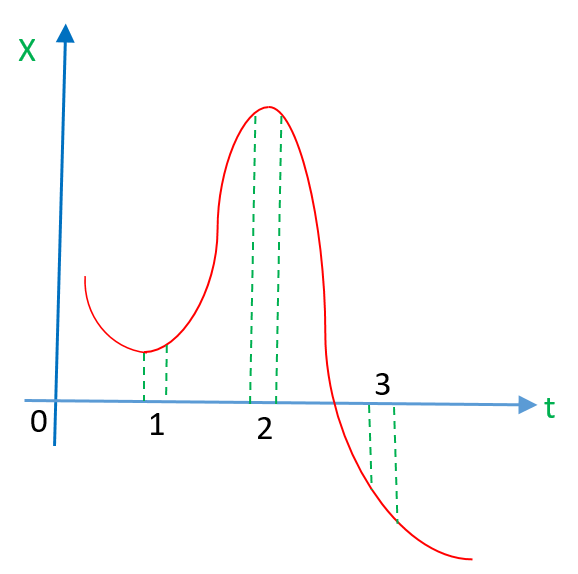
Solution
We known that average speed in a small interval of time is equal to the slope of x-t graph in that interval of time.
The average speed is the greatest in the interval 3 because slope is greatest and the average speed is least in interval 2 because slope is least there (almost zero).
The average speed is positive in intervals 1 because slope of x-t is positive there and average speed is negative in interval 3 because the slope of x-t is negative.
Illustration
Figure shows x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t <0 and on a parabolic path for t >0 ? If not, suggest a suitable physical context for this graph
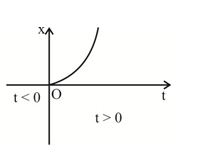
Solution
No, because the x-t graph does not represent the trajectory of the path followed by a particle. From the graph, it is noted that at t =0, x = 0.
The above graph can represent the motion of a body falling freely from a tower under gravity.
Free Fall (Motion under Gravity)
Motion that occurs solely under the influence of gravity is called free fall.
In the absence of air resistance all falling bodies have the same acceleration due to gravity, regardless of their sizes or shapes.
The value of the acceleration due to gravity depends on both latitude and altitude. It is approximately 9.8 m/s2 near the surface of the earth. For simplicity a value of 10 m/s2 is being used normally.
The equations of kinematics are used with proper sign of each quantity
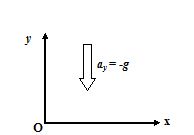
While using the equations of kinematics always remember that all quantities like v , a , S, u are vectors and hence their signs should be considered carefully. For our simplicity we take upward direction as +ve and downward direction as -ve.
Hence acceleration due to gravity is alway -ve because it is always downward irrespective of the motion of the body.
If a body is given an initial velocity upward it should be tken as positive and for downward initial velocity u should be taken as negative.
Hence we may write the equations as under
v = ±u –gt … (5)
y = y0+(±ut) – \displaystyle \frac{1}{2}gt2 … (6)
v2 = \displaystyle u_{{}}^{2}\,-2g\,(±S) … (7)
ALWAYS GIVE SIGN TO THE KNOWN QUANTITY. THE SIGN OF UNKNOWN QUANTITY WILL COME OUT AFTER CALCULATIONS.
Illustration
A stone ‘A’ is dropped from the top of a tower 20 m high. Simultaneously another stone ‘B’ is thrown up from the bottom of the tower so that it can reach just on the top of the tower. What is the distance of the stones from the ground while they pass each other?
Solution
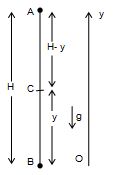
Let t be the time when they pass one another at point C at a height y from the ground.
Applying second equation of motion for both the stones i.e.
S= ut+ \displaystyle \frac{1}{2}g{{t}^{2}}
For stone B, y= ut + \displaystyle \frac{1}{2}(-g){{t}^{2}} … (i)
For stone A, -(H – y) = \displaystyle \frac{1}{2}(-g){{t}^{2}} … (ii)
From (i) and (ii),
H =ut … (iii)
Stone B can reach just the top of tower. Hence it final veloity is zero at the top. We can calculate the velocity of stone B from 3rd equation
\displaystyle v^{2}=u^{2}+2{{a}_{y}}S
Put v = 0, for S = 20 m and ay = -g
therefore from the 3rd equation we get u = 20 m/s
From (iii) t = \displaystyle \frac{{20m}}{{20m/s}}=1\sec .
From equation (i), the required distance (BC) from ground = 20 X 1 – 1/2 10 X 12 = 15 m
Illustration
A particle is thrown vertically upward. Its velocity at half of the height is 10 m/s, then maximum height attained by it is: (g = 10 m/s2)
(A) 8 m
(B) 20 m
(C) 10 m
(D) 16m
Solution
Suppose after travelling distance s, particle has the velocity 10 m/s.
So, v2 = u2– 2as
(10)2 = u2 – 2 x 10s …(1)
At the maximum height, i.e. 2s, v = 0
0 = u2-2g(2s)
u2 = 40s …(2)
From Eqs. (1) and (2), s = 5 m
Hence the total height i.e. 2s = 10 m
therefore option (c) is correct
Objective Assignment
1.
Ball A is dropped to the ground from the top of a tower while another ball B is thrown towards the earth with some initial velocity from same tower. Neglecting air resistance, the acceleration is
(a) same for both the balls
(b) greatest for the dropped ball A
(c) greatest for the ball B
(d)depends upon the sizes of A and B
Ans. (a)
2.
A body moving with a uniform acceleration from the state of rest covers a distance x = 450 m during time t = 6s. At what distance from the initial position is the body four seconds after the beginning of motion ?
(a) 300 m
(b) 200 m
(c) 400 m
(d) 150 m
Ans. (b)
3.
Two bodies of masses m1and m2 fall from heights h1 and h2 respectively. The ratio of their velocities when they hit the ground is
(a) \frac{{{{h}_{1}}}}{{{{h}_{2}}}}
(b) \sqrt{{\frac{{{{h}_{1}}}}{{{{h}_{2}}}}}}
(c) \frac{{{{m}_{1}}{{h}_{1}}}}{{{{m}_{2}}{{h}_{2}}}}
(d) \frac{{{{h}_{1}}^{2}}}{{{{h}_{2}}^{2}}}
Ans. (b)
4.
A parachutist after bailing out falls 50m without friction. When the parachute opens, it decelerates at 2 ms–2. He reaches the ground with a speed 3 ms–1. At what height did he bail out?
(a) 290 m
(b) 340 m
(c) 198 m
(d) 298 m
Ans. (d)
5.
You observe an object covering distances in direct proportion to the square of the time elapsed. The acceleration is
(a) zero
(b) constant
(c) decreasing
(d) increasing
Ans. (b)
6.
If a body having initial velocity zero is moving with a uniform acceleration of 8 m{{s}^{{-2}}}, then the distance traveled by it in fifth second will be
(a) zero
(b) 36 m
(c) 40 m
(d) 100 m
Ans. (b)
7.
A cricket ball and a tennis ball are simultaneously thrown upwards from the ground with equal initial speeds. Ignoring air resistance, which of the following statements is correct?
(a) Both the balls travel the same distance in the same time.
(b) Tennis ball rises the highest.
(c) Tennis ball is in flight the longest.
(d) Tennis ball has a smaller impact speed.
Ans. (a)
8.
A stone falls from a balloon that is descending at a uniform rate of 12 ms–1. Its velocity after 10 seconds from the point of release is
(a) 114ms–1
(b) 113ms–1
(c) 112 ms–1
(d) 115ms–1
Ans. (c)
9.
The displacement of a freely falling body is proportional to the
(a) time of fall
(b) square of the time of fall
(c) mass of the body
(d) square of mass of the body
Ans. (b)
10.
A man standing at the top of a building throws a ball vertically upward with a velocity of 10 ms–1. The ball reaches the ground 4 s later. What is the maximum height reached by the ball? How high is the building?
(a) 6 m above the building, 40 m
(b) 7 m above the building, 50 m
(c) 9 m above the building, 60 m
(d) 5 m above the building, 40 m’
Ans. (c)
11.
A car from rest start accelerating uniformly to a speed of 144km{{h}^{{-1}}} over a distance of 400 m. The time taken is
(a) 5 s
(b) 10 s
(c) 15 s
(d) 20 s
Ans. (d)
12.
A ball falls freely from rest. The ratio of the distances traveled in first, second, third and fourth second is
(a) 1 : 1 : 1 : 2
(b) 1 : 1 : 1 : 3
(c) 1 : 2 : 3 : 4
(d) 1 : 3 : 5 : 7
Ans. (d)
13.
Two bodies are thrown vertically upwards with their initial velocity in the ratio 2 : 3. Then the ratio of the maximum height attained by them is
(a) 1 : 1
(b) 4 : 9
(c) 2 : 3
(d) \sqrt{2}:\sqrt{3}
Ans. (b)
14.
A stone is dropped under gravity from rest from a height and it travels a distance \frac{{9h}}{{25}} in the last second. What is the height h? ( g = 9.8 ms-2 )
(a) 145 m
(b) 100 m
(c) 122.5 m
(d) 100 m
Ans. (c)
15.
A car starts from rest with an acceleration of 2 ms-2 for 5 sec and then move with constant velocity for next 5 sec.and finally retard at 2 ms-2 to come to rest. Find its average velocity.
(a) 5.8 m/s
(b) 6.67 m/s
(c) 8.76 m/s
(d) 9.62 m/s
Ans. (b)
16.
A car starts from rest and moves with constant acceleration. The ratio of distance covered by the car in nth second to that covered in n second is
(a) \frac{{2n-1}}{{2{{n}^{2}}}}
(b) \frac{{{{n}^{2}}}}{{2n-1}}
(c) \frac{{2n-1}}{{{{n}^{2}}}}
(d) 1:n
Ans. (c)
17.
P, Q and R are three balloons ascending with velocities u, 4 uand 8 u respectively. If stones of the same mass be dropped from each, when they are at the same height, then
(a) stone from P reaches the ground first
(b) stone from Q reaches the ground first
(c) stone from R reaches the ground first
(d) all reach at same time
Ans. (a)
18.
A body covers 4.9m, 14.7m, 24.5m and 34.3m in the successive seconds of motion. The acceleration of the body is
(a) 2.7\mathbf{m}{{\mathbf{s}}^{{-\mathbf{2}}}}
(b) 4.9\mathbf{m}{{\mathbf{s}}^{{-\mathbf{2}}}}
(c) 9.8\mathbf{m}{{\mathbf{s}}^{{-\mathbf{2}}}}
(d) 19.6\mathbf{m}{{\mathbf{s}}^{{-\mathbf{2}}}}
Ans. (c)
19.
A particle starts from rest and moves with constant acceleration. Its distance x and velocity v are related as
(a) x\propto v
(b) x\propto {{v}^{2}}
(c) x\propto {{v}^{3}}
(d) x\propto {{v}^{4}}
Ans. (b)
20.
Choose the correct option
(a) Acceleration means speeding up of a body
(b) During negative acceleration of a body the speed may increase
(c) If the velocity is nonzero , the acceleration must also be nonzero
(d) The sign of acceleration and velocity should always be same.
Ans : (b)
Subjective Assignment
1.
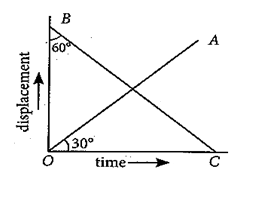
In the given figure two straight lines drawn on the same v-t graph makes angles 30º and 60º with the velocity axis. Which line represents greater acceleration? What is the ratio of the two acceleration?
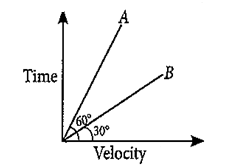
Ans. aA = tan30o = 1/√3 , aB = tan60o = √3 .
2.
A ball is thrown vertically upwards. Draw its height-time and velocity-time graph.
3.
The displacement of particle is proportional to the cube of time elapsed. How does the acceleration of the body depend on time elapsed?
Ans. given S ∝ t3. On diffrentiating it two times we get acceleration a ∝ t.
4.
A particle starts from rest, and its acceleration (a) plotted against time(t) is shown here. Plot the corresponding velocity (v) against time (t). Also plot the corresponding displacement (s) against time(t).
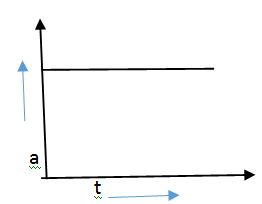
Ans. The graph shows that acceleration is constant hence three equations of motion are applicable. So graph between velocity and time is given by the equation v=u+at which represent a straight line with positive slope. And graph between displacement and time is given by the equation S=ut + 1/2at2 which represent a parabola.
5.
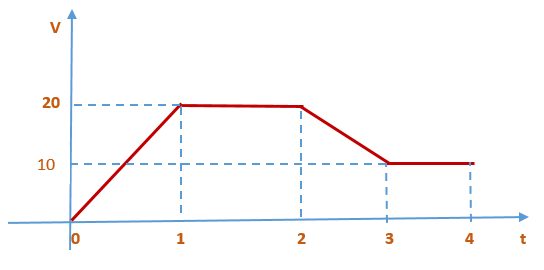
The following figure represents the velocity Vs time graph of a particle moving in a straight line. [velocity in m/sec and time in sec ]
(a)
Did the particle ever move with uniform velocity?
(b)
Did the particle ever move with uniform acceleration?
(c)
What is the distance traversed by the particle in 4 second?
Ans.
(a) yes from t=1 to t=2 and from t=3 to t=4, velocity is uniform
(b) yes from t=0 to t=1 and from t=2 to t=3, acceleration is uniform
(c) Distance = area under the graph from t=0 to t=4 and that is 55m
6.
Describe the following graphs for uniformly accelerated motion
(a) velocity – time graph
(b) Displacement – time graph
(c) acceleration – time graph
Ans.
(a) using equation v = u + at , the graph between v and t is a straight line with positive slope
(b) using equation S=ut + 1/2at2, the graph between S and t is a parabola with positive slope
(c) since acceleration is constant so its graph is a straight line parallel to time axis.
7.
Figure gives a speed-time graph of a particle in one dimensional motion along a constant direction. Three equal intervals of time are shown.
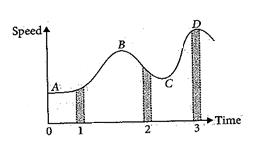
(i)
In which interval is the average acceleration greatest in magnitude?.
(ii)
In which interval is the average speed greatest?
(iii)
Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals.
(iv)
What are the accelerations at the points A, B> C and D?
Ans.
(i) The change in the speed with time is maximum in interval 2. Therefore, the average acceleration is greatest in magnitude in interval 2.
(ii) The average speed is maximum in interval 3.
(iii) The sign of velocity is positive in intervals 1, 2 and 3. The acceleration depends on the slope. The acceleration is positive in intervals 1 and interval 3, as the slope is positive. The acceleration is negative in interval 2, as the slope is negative.
(iv) Acceleration at A, B, C and D is zero since the slope is parallel to the time axis at these instants.
8.
Two bodies of different masses ml and m2 are dropped from two different height a and b. What is the ratio of time taken by the two to drop through these distance?
Ans. Same for both
9.
Plot a graph between velocity and time for a ball dropped on the ground from certain height and rebounce back to same height.
10.
What is the ratio of the distances travelled by a body, falling freely from rest, in the first, second and third seconds of its fall?
Ans. 1:3:5
11.
Draw position-time graph for the motion of a body having
(i) uniform positive acceleration,
(ii) uniform negative acceleration and zero acceleration.
12.
Draw the position – time graph for following cases when:
(a)
Object is moving with positive and constant acceleration.
(b)
An object is under free fall.
13.
The speed-time graph for a particle, moving along a straight line, is shown in the figure. Find out the average speed of the particle between the time intervals:
(i)t= 0 and t = 10s
(ii)t = 2s and t = 6s
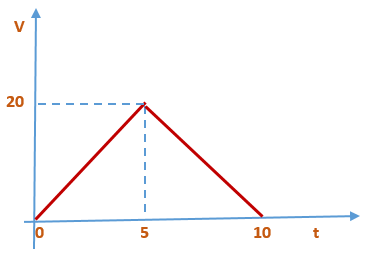
Ans.
(i) 10m/sec
(ii) 15m/sec
14.
Derive the expression for distance travelled’ by uniformly accelerated body in nth second.
15.
A ball is dropped from the top of the tower of height h. The total distance covered by the ball in the last second is one-fourth of the total height h. What is h?
(Take g = 10 m/s2).
Ans. \displaystyle \frac{{20}}{{{{{\left( {2-\sqrt{3}} \right)}}^{2}}}}m
16.
A balloon is ascending at the rate of 4.9 m/s. A packet is dropped from balloon when situated at a height of 245 m. How long does the packet take to reach the ground? What is its final velocity?
Ans. 7.5sec , 70.1 m/sec downward
17.
The velocity of a train increases at a constant rate a from 0 to v and then remains constant for some time interval and then finally decreases to zero at a constant rate b. If the total distance covered by the particle be x, find the total time of journey.
Ans. \displaystyle t\,=\,\frac{x}{v}\,+\,\frac{v}{2}\,\left[ {\frac{1}{\alpha }+\frac{1}{\beta }} \right].
18.
A car starts from rest and accelerates uniformly for 10 s to a velocity of 8 m s-1. It then runs with constant velocity and is finally brought to rest in 64 m with a constant retardation. The total distance covered by the car is 584 m. Find the value of acceleration, retardation and total time taken.
Ans. 0.8ms-2 , – 0.5ms-2 , 86sec
20.
Two ends of a train moving with a constant acceleration passes a certain point with velocities u and v. Show that the velocity with which the middle point of the train passes the same point is \displaystyle \sqrt{{\frac{{{{u}^{2}}+{{v}^{2}}}}{2}}}.
21.
A ball is released from the top of tower of height h metres. It takes T seconds to reach the ground. What is the height of the ball at T/3 second?
Ans. 8h/9
22.
The displacement –time graph of two bodies A and B are represented by OA and BC respectively. What is the ratio of velocities of A and B ?
Ans. -1