Video Lectures
Theory For Making Notes
Forces in Nature can be divided into two categories depending on their work CONSERVATIVE and NON CONSERVATIVE Forces. Here are some important points.
Conservative Forces
Examples are Electrostatic forces, gravitational forces, elastic forces, etc and all the central forces.
1.
In conservative field, work done by the force (also called line integral of the force i.e. \int{{\overrightarrow{F}.d\overrightarrow{{l\,}}}}) between any two points say A and B is independent of the path followed by the body.
\underset{\begin{smallmatrix} \text{Path I}\end{smallmatrix}}{\mathop{{{{W}_{{A\to B}}}}}}\,=\underset{\begin{smallmatrix} \text{Path II} \end{smallmatrix}}{\mathop{{{{W}_{{A\to B}}}}}}\,=\underset{\begin{smallmatrix} \text{Path III} \end{smallmatrix}}{\mathop{{{{W}_{{A\to B}}}}}}\,
or
\underset{\begin{smallmatrix} \text{Path I} \end{smallmatrix}}{\mathop{{\int{{\overrightarrow{F}.d\overrightarrow{{l\,}}}}}}}\,=\underset{\begin{smallmatrix} \text{Path II}\end{smallmatrix}}{\mathop{{\int{{\overrightarrow{F}.d\overrightarrow{{l\,}}}}}}}\,=\underset{\begin{smallmatrix} \text{Path III} \end{smallmatrix}}{\mathop{{\int{{\overrightarrow{F}.d\overrightarrow{{l\,}}}}}}}\,
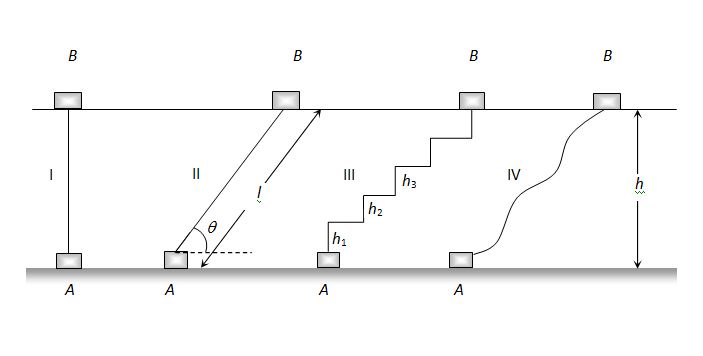
For example If a body of mass m lifted to height h from the ground level steadily and slowly by four different paths as shown in the figure
Then work done by external force F against the conservative force of gravity (mg) through different paths can be calculated as follows. Here F is applied vertically upward in each case
In the first path
{{W}_{I}}=F.\,s=mg\times h=mgh
In the second path
\displaystyle {{W}_{{II}}}=F.\,s=mg\times l\times \cos (90-\theta )=mg\times l\sin \theta =mgh
In the third path
The body is taken in n steps of height h1 , h2 , h3 , ………. from A to B
{{W}_{{III}}}=mg{{h}_{1}}+0+mg{{h}_{2}}+0+mg{{h}_{3}}+0+mg{{h}_{4}}+ ……. ( note 0 work done for horizontal displacements)
=mg({{h}_{1}}+{{h}_{2}}+{{h}_{3}}+{{h}_{4}})=mgh
{{W}_{{IV}}}=\int{{\overrightarrow{F}.\,d\overrightarrow{{s\,}}}}=mgh
It is clear that \displaystyle {{W}_{I}}={{W}_{{II}}}={{W}_{{III}}}={{W}_{{IV}}}=mgh.
Further if the body is brought back to its initial position A, similar amount of work (energy) is released from the system, it means {{W}_{{AB}}}=mgh and {{W}_{{BA}}}=-mgh.
Hence the net work done against gravity over a round trip is zero.
{{W}_{{Net}}}={{W}_{{AB}}}+{{W}_{{BA}}} =mgh+(-mgh)=0
Hence the gravitational force is conservative in nature.
2.

In conservative field work done by the force (line integral of the force i.e. \int{{\overrightarrow{F}.d\overrightarrow{{l\,}}}}) over a closed path/loop is zero.
{{W}_{{A\to B}}}+{{W}_{{B\to A}}}=0
or \oint{{\vec{F}.d\vec{l}=0}}
3.
The Potential energy of a system decreases when a conservative force do work on the system. Hence \displaystyle {{W}_{{(conservative.force)}}}=-\Delta U here ∆U is the change in potential energy
In differential form it can be written as \displaystyle dW=-dU
Or \displaystyle F.dl=-dU
and hence \displaystyle F=-\frac{{dU}}{{dl}} —————– (1)
this shows that the negative rate of change of Potential energy with position is equal to the conservative force acting on the body.
So always remember that only conservative forces can change the potential energy of a system or body.
If on a system conservative forces are acting along three axis i.e. x,y,z then the equation (1) can be rewritten in partial differential form along three axis as follows
\displaystyle {{F}_{x}}=-\frac{{\partial U}}{{\partial x}},{{F}_{y}}=-\frac{{\partial U}}{{\partial y}},{{F}_{z}}=-\frac{{\partial U}}{{\partial z}}
Non-conservative forces:
A force is said to be non-conservative if work done by or against the force in moving a body from one position to another, depends on the path followed between these two positions and for complete cycle this work done may or may not be zero.
Example: Frictional force, Viscous force, Airdrag etc.
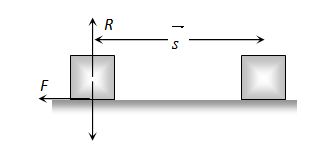
If a body is moved from position A to another position B on a rough table, work done against frictional force shall depend on the length of the path between A and B and not only on the position A and B.
{{W}_{{AB}}}=\mu mgs (Here work is calculated in ground frame)
Further if the body is brought back to its initial position A, work has to be done against the frictional force, which opposes the motion. Hence the net work done against the friction over a round trip is not zero. {{W}_{{BA}}}=\mu mgs.
\therefore \,{{W}_{{Net}}}={{W}_{{AB}}}+{{W}_{{BA}}}=\mu mgs+\mu mgs=2\mu mgs\ne 0.
i.e. the friction is a non-conservative force.
Also the potential energy associated with the non-conservative field is not defined.
Remember that when an external agent do work against a non-conservative force like friction , the potential energy of the system does not change but all the work is lost in the form of heat.
Practice Questions (Level-1)
1.
The negative of the space rate of change of potential energy is equal to
(a) force acting on the particle in the direction of displacement
(b) acceleration of the particle, perpendicular to displacement
(c) power
(d) impulse
Ans (a)
Q.2
A spring of force constant 10 N/m has initial stretch 0.2 m. In changing the stretch to
0.25 m, the increase in PE is about
(a) 0.1 J (b) 0.2 J (c) 0.3 J (d) 0.5 J
Ans. (a)
Practice Questions (Level-2)
1.
The potential energy of a particle in a certain field has the form, U=\frac{a}{{{{r}^{2}}}}-\frac{b}{r} where a andb are positive constants, r is the distance from the centre of the field. The distance of the particle in the stable equilibrium position is
(a) a/b
(b) –a/b
(c) 2a/b
(d) –2a/b
Ans (c)
Q.2
A long spring is stretched by x cm. Its PE is U. If the spring is stretched by Nx cm the PE stored in it will be
(a) \frac{U}{N}
(b) NU
(c) N2U
(d) \frac{U}{{{{N}^{3}}}}
Ans. (c)
Q.3
Two springs have their force constants as K1 and K2 (K1 > K2). The work done, when both are stretched by the same amount of length will be
(a) equal
(b) greater for K1
(c) greater for K2
(d) given data is incomplete
Ans. (b)
Q.4
A particle is moving in a conservative force field from point A to point B. UA and UB are the potential energies of the particle at points A and B and WC is the work done in the process of taking the particle from A to B.
(a) WC = UB – UA
(b) WC = UA – UB
(c) UA = UB
(d) UB > UA
Ans. (b)


