Video Lecture
Theory For Notes Making
Plantery Motion And Kepler’s Laws
Consider a satellite of mass m revolving in a circle around the earth. If the satellite is at a height h above the earth’s surface, the radius of its orbit is r = R + h, where R is the radius of the earth. The gravitational force between m and M provides the necessary centripetal force for circular motion.
Orbital velocity
Consider a satellite moving with a speed voin a circular orbit of radius r around the earth at a height h from its surface.
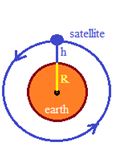
As we know that the earth’s gravitational force provides the necessary centripetal force to the satellite
Hence \frac{{mv_{0}^{2}}}{r}=\frac{{GMm}}{{{{r}^{2}}}} \frac{{mv_{0}^{2}}}{r}=\frac{{GMm}}{{{{r}^{2}}}} ( where r=R+h))
or, v_{0}^{2}=\frac{{GM}}{r}c
{{v}_{0}}=\sqrt{{\frac{{GM}}{r}}} …(1)
But {{v}_{0}}=\sqrt{{\frac{{GM}}{r}}}
{{v}_{0}}=\sqrt{{\frac{{GM}}{R+h}}} …(2)
Let gh be the value of acceleration due to gravity at a height h above the free surface of Earth.
Then, m{{g}_{h}}=\frac{{GMm}}{{{{{(R+h)}}^{2}}}}
or, GM={{g}_{h}}{{(R+h)}^{2}}
From equation (2), {{v}_{0}}=\sqrt{{\frac{{{{g}_{h}}{{{(R+h)}}^{2}}}}{{R+h}}}}
or, \displaystyle {{v}_{0}}=\sqrt{{{{g}_{h}}(R+h)}} …(3)
If g be the value of acceleration due to gravity on the surface of Earth, then g=\frac{{GM}}{{{{R}^{2}}}}
Also, {{g}_{h}}=\frac{{GM}}{{{{{(R+h)}}^{2}}}}
\frac{{{{g}_{h}}}}{g}=\frac{{GM}}{{{{{(R+h)}}^{2}}}}\times \frac{{{{R}^{2}}}}{{GM}}=\frac{{{{R}^{2}}}}{{{{{(R+h)}}^{2}}}}
or {{g}_{h}}=\frac{{g{{R}^{2}}}}{{{{{(R+h)}}^{2}}}}
from equation (3), {{v}_{0}}=\sqrt{{\frac{{g{{R}^{2}}}}{{{{{(R+h)}}^{2}}}}(R+h)}}
or {{v}_{0}}=R\sqrt{{\frac{g}{{R+h}}}}
Equation (1), (2), (3) and (4) give different expressions for the orbital velocity of a satellite.
Special Case. If the satellite is close to Earth, say at a height of 100-200 kg, then h may be regarded as zero and gh may be considered to be equal to g.
In this case, from equation (3), {{v}_{0}}=\sqrt{{gR}}
Substituting values,
{{v}_{0}}=\sqrt{{9.81\times 6400\times 1000}}\ \text{m}{{\text{s}}^{{-1}}}
=\sqrt{{62784000}}\ \text{m}{{\text{s}}^{{-1}}}=7923.6\text{m}{{\text{s}}^{{-1}}}=7.9\text{km}\,{{\text{s}}^{{-1}}}
Note: For an orbit close to the surface of the Earth, escape velocity, {{v}_{e}}=\sqrt{{2gR}}=\sqrt{2}orbit velocity v0.
Important
(i) Orbital velocity is independent of the mass of the orbiting body and is always along the tangent to the orbital.
(ii) Close to the surface of the earth, r = R as h = 0.
{{V}_{0}}=\sqrt{{\frac{{GM}}{R}}}=\sqrt{{gR}}=\sqrt{{10\times 6.4\times {{{10}}^{6}}}}\approx \ 8\ \text{km/s}
(iii) Close to the surface of the planet
{{V}_{0}}=\sqrt{{\frac{{GM}}{R}}}=\frac{{{{V}_{e}}}}{{\sqrt{2}}}
i.e., {{V}_{e}}=\sqrt{2}{{V}_{0}}
Time period of a satellite
As Time=\frac{{Dis\tan ce}}{{Speed}}
therefore T=\frac{{\text{circumference}\ \text{of}\ \text{circular}\ \text{orbit}}}{{\text{orbital}\ \text{velocity}}}
or, T=\frac{{2\pi r}}{{{{v}_{0}}}}
or, T=\frac{{2\pi \,(R+h)}}{{{{v}_{0}}}} [\because \ \ r=R+h]
or, T=2\pi (R+h)\sqrt{{\frac{{R+h}}{{GM}}}} \left[ {\because \ \ {{v}_{0}}=\sqrt{{\frac{{GM}}{{R+h}}}}} \right]
or, T=2\pi \sqrt{{\frac{{{{{(R+h)}}^{2}}}}{{GM}}}}
Also, T=2\pi \sqrt{{\frac{{{{{(R+h)}}^{2}}(R+h)}}{{GM}}}}
or, T=2\pi \sqrt{{\frac{{R+h}}{{{{g}_{h}}}}}} \left[ {\because \ \ gh=\frac{{GM}}{{{{{(R+h)}}^{2}}}}} \right]
But GM=g{{R}^{2}}
From equation, T=2\pi \sqrt{{\frac{{{{{(R+h)}}^{3}}}}{{g{{R}^{2}}}}}} ————– (A)
Equations give different expressions for the time period of a satellite.
Special Case. If the satellite is orbiting very close to the Earth, then
T=2\pi \sqrt{{\frac{{{{R}^{3}}}}{{GM}}}} and T=2\pi \sqrt{{\frac{R}{g}}}.
Height of satellite
From equation (A) {{T}^{2}}=4{{\pi }^{2}}\frac{{{{{(R+h)}}^{3}}}}{{g{{R}^{2}}}} or {{(R+h)}^{3}}=\frac{{g{{R}^{2}}{{T}^{2}}}}{{4{{\pi }^{2}}}}
or R+h={{\left[ {\frac{{g{{R}^{2}}{{T}^{2}}}}{{4{{\pi }^{2}}}}} \right]}^{{1/3}}}
or h={{\left[ {\frac{{g{{R}^{2}}{{T}^{2}}}}{{4{{\pi }^{2}}}}} \right]}^{{1/3}}}-R
Angular momentum of a satellite (L)
In case of satellite motion, angular momentum will be given by
L=mvr=mr\ \sqrt{{\frac{{GM}}{r}}}
L={{\left( {{{m}^{2}}GMr} \right)}^{{1/2}}}
important
In case of satellite motion, the net force on the satellite is centripetal force. The torque of this force about the center of the orbit is zero. Hence, angular momentum of the satellite is conserved, i.e., L = constant.
Energy of a satellite
The P.E. of a satellite is
U =mV =-\frac{{GMm}}{r} \,\,\left[ {\because \ V=-\frac{{GM}}{r}} \right]
The kinetic energy of the satellite is
K=\frac{1}{2}mv_{0}^{2}\ \ \ =\frac{{GMm}}{{2r}} \ \ \ \ \left[ {\because \ {{v}_{0}}=\sqrt{{\frac{{GM}}{r}}}} \right]
Total mechanical energy of the satellite = -\frac{{GMm}}{r}+\frac{{GMm}}{{2r}}=-\frac{{GMm}}{{2r}}
Important
(i) We have, \frac{K}{E}=-1 i.e., K = –E
Also, \frac{U}{E}=2
U = 2E
therefor E = -K = U/2
(ii) Total energy of a satellite in its orbit is negative. Negative energy means that the satellite is bound to the central body by an attractive force and energy must be supplied to remove it from the orbit to infinity.
Binding energy of the satellite
The energy required to remove the satellite from its orbit to infinity is called binding energy of the satellite, i.e.,
Binding energy = – E =\frac{{GMm}}{{2r}}
Weightlessness in a satellite
In the frame of reference of a satellite the astronauts experience the following forces
1.
The gravitational force of the planet around which the satellite is moving = \frac{{GM{{m}_{a}}}}{{{{r}^{2}}}} and it acts along the radius toward the center of the orbit.
2.
The centrifugal force due to circular motion of the satellite = \frac{{{{m}_{a}}v_{o}^{2}}}{r} where vo is the orbital velocity and is given by {{\nu }_{o}}=\sqrt{{\frac{{GM}}{r}}}, this force acts radially outward i.e. away from the center of the orbit.
Hence substituting vo we get the centrifugal force = \displaystyle \frac{{{{m}_{a}}v_{o}^{2}}}{r}=\frac{{GM{{m}_{a}}}}{{{{r}^{2}}}} which is exactly equal to the
gravitational inward force therefore the net force acting on the astronauts becomes zero hence they feel weightlessness.
Uses of artificial satellites
(i) To study various phenomena in the outer regions of the Earth’s atmosphere.
(ii) To study various phenomena connected with sea.
(iii) For communication purposes.
(iv) For weather forecasting.
Geostationary or Synchronous satellite
A geostationary satellite is so named because it appears to be stationary to an observer on the Earth. This satellite is also named as synchronous satellite because the angular speed of the satellite is synchronized with the angular speed of Earth about its axis. When such a satellite is used for communication purposes, it is also known as communication satellite.
In order that a satellite may appear stationary to an observe on the Earth, the following conditions must be satisfied.
(i) It should be at a height of nearly 36000 km above the equator.
(ii) It should revolve in an orbit which is concentric and coplanar with the equatorial plane. So, the plane of the orbit of the satellite in normal to the axis of rotation of the Earth.
(iii) The sense of rotation of the satellite should be the same as that of the Earth about its own axis. So, the satellite should orbit around the Earth from west to east as does the Earth. Its orbit velocity is nearly 3.1 km s–1.
(iv) The orbital period of the satellite, i.e., the time taken by the satellite to complete one revolution around the Earth is the same as that of the Earth about its own axis i.e., 24 hours.
Illustration
Calculate the orbital velocity of a satellite revolving at a height h above the earth’s surface if h = R. Also calculate the time-period of this satellite. (g = 9. m/s2,
R = 6400 km)
Solution:
For the orbital velocity in a circular orbit, we have
v=\sqrt{{\frac{{GM}}{r}}}=\sqrt{{\frac{{GM}}{{R+h}}}} (Qr = R + h)
v=\sqrt{{\frac{{g{{R}^{2}}}}{{2R}}}}=\sqrt{{\frac{{gR}}{2}}} (QGM = gR2 and h = R) Þ v=\sqrt{{\frac{{9.8\,\,\times \,6400\times {{{10}}^{3}}}}{2}}} = 5.6 km/s
Time period = T=\frac{{2\pi r}}{v}=\frac{{2\pi \,(2R)}}{{4\sqrt{2}\times {{{10}}^{3}}}}
T=\frac{{4\pi \times 6400\times {{{10}}^{3}}}}{{4\sqrt{2}\times {{{10}}^{3}}}} =3.95\ \text{hrs}
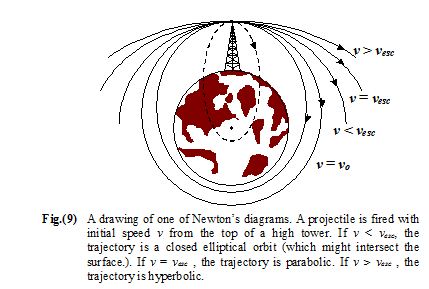
Bound and Unbound Trajectories
Suppose that a cannonball is fired from the peak of very tall tower with speed v. Let us consider the shapes of the paths for various values of v.
If the ball is located at a distance r from the center of the earth, the speed that is required to escape from the point is given by
vesc= \sqrt{{\frac{{2GM}}{r}}}
For a circular orbit of radius r the orbital speed is vo= \sqrt{{\frac{{GM}}{r}}}
(a) When v <vo, the orbit is elliptical, with the peak as the apogee (the farthest point from earth). If v is too small, the projectile will strike the earth.
When v = vo, the orbit is circular.
When vesc>v >vo, the orbit is again an ellipse, but now the peak is the perigee (the closest point to earth).
(b) When v = vesc= \sqrt{2}vo, the path is parabolic and is not a closed orbit. The object is not bound.
(c) When v >vesc, the path is hyperbola and not closed. The object is not bound.
Kepler’s Laws
First Law
The planets move around the sun in elliptical orbits with the sun at one focus.
An ellipse with two foci F1 and F2 is shown in the figure.
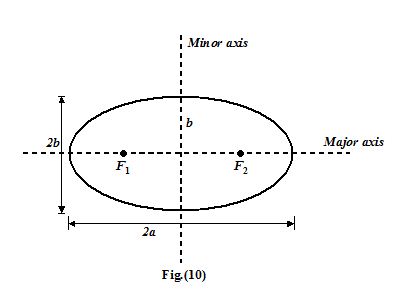
A circle is a special case in which the foci coincide at the center. The short dimension is called the minor axis and has length 2b; the long dimension is called the major axis and has length 2a. The closest point P, in the orbit to the sun is called the perihelion; the farthest point A, is called the aphelion.
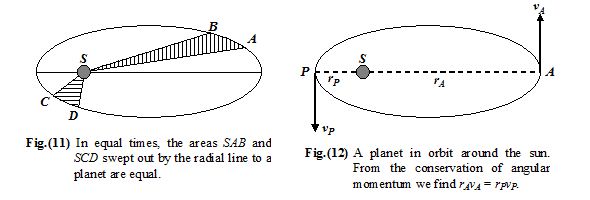
Second Law
The line joining the sun to a planet sweeps out equal areas in equal time.
Suppose that in a given time interval a planet moves from A to B as shown in the figure, and from C to D during another time interval. According to the second law the areas SAB and SCD are equal. The speed of the planet, therefore, must vary during its orbit. It is greatest at the perihelion, and least at the aphelion. In example (5), this law is shown to be a consequence of the conservation of angular momentum.
Third Law
The square of the period of planet is proportional to the cube of its mean distance from the sun.
The mean distance turns out to be the semi-major axis, a.
Mathematically, T2∝ a3
or T2 = ka3
where k is a constant that applies to all planets.
Illustration
According to Kepler’s second law of planetary motion, the line joining the sun to a planet sweeps out equal areas in equal time intervals. Show that this is a consequence of the conservation of angular momentum. The path of the planet is an ellipse.
Solution
The gravitational force exerted by the sun on a planet is a central force – it acts along the line joining the two bodies, as shown in Fig(13). The torque on the planet is
\displaystyle \vec{\tau }= \displaystyle \vec{r} ´ \displaystyle \vec{F}= rF sin 180° \displaystyle \hat{n} = 0
which means that its angular momentum is constant. The constancy in direction implies that the plane of the orbit does not change. The constancy in magnitude leads to the “law of areas.”
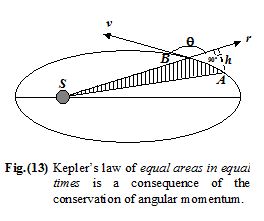
In a time interval Dt, the planet moves from A to B by a distance AB = vDt. The height of the triangle SAB is
h = AB sin(180 -θ)° = vDt sinq
Thus, its area is
DA = \frac{1}{2}rh = \frac{1}{2}rvDt sinq
so,
\frac{{\Delta A}}{{\Delta t}}= \frac{1}{2}rv sinq (i)
The angular momentum of the planet is
l = rp sinθ = mrv sinθ (ii)
Combining (i) and (ii) we see that
\frac{{\Delta A}}{{\Delta t}}= \frac{L}{{2m}} = constant
The rate at which the radial line sweeps out area is constant. Or, equivalently, the radial line sweeps out equal areas in equal time intervals.
Objective Assignment
1.
Which of the following graphs represents the motion of a planet moving about the sun
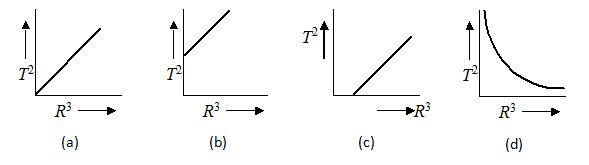
Ans (a)
2.
If r represents the radius of the orbit of a satellite of mass m moving round a planet of mass M, the velocity of the satellite is given by
(a) v2 = GM/r
(b) v2 = GM m/r
(c) v = GM/r
(d) v = 2GM/r
Ans (a)
3.
If the speed of a satellite orbiting near the surface of the earth is changed from Voto ( \sqrt{{1.5}}) Vo. What is most likely to happen
(a) it will revolve in a circular orbit of greater radius
(b) it will escape from the earth
(c) its orbit will change from circular to elliptic
(d) it will remain in the same circular orbit
Ans (c)
4.
A satellite is revolving round the earth in a circular orbit whose radius is R, work done by gravitational force in the revolution is
(a) zero
(b) 2mgR2
(c) mgR2
(d) mgR
Ans (a)
5.
In order to find time the astronauts orbiting in an earth satellite should use
(a) a pendulum clock
(b) a watch having main spring to keep it going
(c) either a watch or a pendulum clock
(d) neither a watch nor a pendulum clock
Ans (b)
6.
An orbiting satellite will escape if
(a) its speed is increased by 41%
(b) its speed in the orbit is made ( \sqrt{{1.5}}) times of its initial value
(c) if it stops moving in the orbit
(d) none of these
Ans a
7.
Which of the following quantities remain constant in a planetary motion (consider elliptical orbits) as seen from the sun?
(a) speed
(b) angular speed
(c) kinetic energy
(d) angular momentum
Ans (d)
8.
The fig. shows the motion of a planet around the sun in an elliptical orbit with sun at the focus. The shaded are A and B area also shown in the figure which can be assumed to equal. If t1 and t2 represent the time taken for the planet to move from a to b and c to d respectively, then
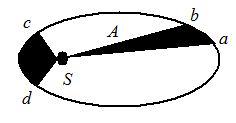
(a) t1>t2
(b) t1<t2
(c) t1 = t2
(d) from given information the relation between t1 and t2 cannot be determined
Ans (c)
9.
A satellite A of mass m is at a distance r from the centre of the earth and another satellite B of mass 2 m is at a distance 2r from the earth’s centre. Their time periods are in the ratio
(a) 1 : 2
(b) 1 : 4
(c) 1 : 16
(d) 1 : 2 \sqrt{2}
Ans (d)
10.
A satellite which is geostationary in a particular orbit is taken to another orbit. Its distance from the centre of earth in the new orbit is 2 times that of the earlier orbit. The time period in the second orbit is
(a) 48 hours
(b) 48 \sqrt{2} hours
(c) 24 hours
(d) 24 \sqrt{2} hours
Ans (b)
11.
An artificial satellite moving in a circular orbit around the earth has a total (kinetic + potential) energy Eo. Its potential energy is
(a) –Eo
(b) 1.5 Eo
(c) 2Eo
(d) Eo.
Ans c
12.
A planet of mass m moves around the Sun of mass M in an elliptical orbit. The maximum and minimum distance of the planet from the Sun are r1 and r2 respectively. The time-period of the planet is proportional to
(a) r_{1}^{{3/2}}
(b) r_{2}^{{3/2}}
(c) {{\left( {{{r}_{1}}+{{r}_{2}}} \right)}^{{3/2}}}
(d) {{\left( {{{r}_{1}}-{{r}_{2}}} \right)}^{{3/2}}}
Ans (c)
13.
A satellite is revolving around the sun in a circular orbit with uniform velocity v. If the gravitational force suddenly disappears, the velocity of the satellite will be
(a) zero
(b) v
(c) 2v
(d) infinity
Ans (b)
14.
Figure shows a planet in elliptical orbit around the sun S. Where is the kinetic energy of the planet maximum?
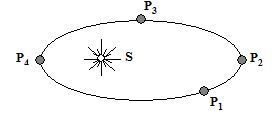
(a) P1
(b) P2
(c) P3
(d) P4
Ans (d)
15.
In the above question, the angular momentum of the planet about sun is
(a) maximum at P2
(b) maximum at P1
(c) minimum at P2
(d) equal at all the points
Ans (d)
16.
An earth satellite of mass m revolves in a circular orbit at a height h from the surface of the earth. R is the radius of the earth and g is acceleration due to gravity at the surface of the earth. The velocity of the satellite in the orbit is given by
(a) \frac{{g{{R}^{2}}}}{{\left( {R+h} \right)}}
(b) gR
(c) gR\left( {R+h} \right)
(d) \sqrt{{\frac{{g{{R}^{2}}}}{{\left( {R+h} \right)}}}}
Ans (d)
Subjective Assignment
1.
A rocket is fired from the earth towards the sun. At what point on its path is the gravitational force on the rocket zero? Mass of sun = 2 x 1030 kg. Mass of earth = 6 x 1024 kg. Neglect the effect of other planets. Orbital radius of earth = 1.5 x 1011 m.
Ans- 2.59 x 108 m
2.
A Saturn year is 29.5 times the earth year. How far is the Saturn from the sun of the earth is 1.5 x 108 km away from the sun ?
Ans-1.43 x 109 km
3.
A space-ship is stationed on Mars. How much energy must be expended on the spaceship to rocket it out of the solar system? Mass of the spaceship = 1000 kg, Mass of the Sun = 2 x 1030 kg, Mass of the Mars = 6.4 x 1023 kg, Radius of Mars = 3395 km. Radius of the orbit of Mars = 2.28 x 1011 m, G = 6.67 x 10-11 Nm2kg-2.
Ans- 5.98 x 1011 J
4.
A satellite orbits the earth at a height of 600 km from its surface. Compute its
(a)
kinetic energy
Ans- 8.57 x 109 J
(b)
potential energy
Ans– 17.4 x 109 J
(c)
Total energy from the following data
Ans– 8.57 x 109 J
5.
A sky lab of mass 2 x 103 kg is first launched from the surface of earth in a circular orbit of radius 2R (from the centre of earth) and then it is shifted from this circular orbit to another circular orbit of radius 3R. Calculate the minimum energy required
(a)
to place the lab in the first orbit
Ans – 9.6 x 1010 J
(b) to shift the lab from first orbit to the second orbit Given R = 6400 km and g = 10 m/s2.
Ans- 1.1 x 1010 J
