Video Lecture
Theory For Making Notes
Nucleus
So far the only knowledge of nucleus we have is that it is a tiny positively charged object whose primary contributions are to provide the atom with most of its mass and to hold its electrons in captivity. The chief properties of atoms, molecules, solids and liquids can all be traced to the behaviour of atomic electrons and not to the behaviour of nuclei. However, the nucleus turns out to be of paramount importance in the grand scheme of things. To start with the very existence of the various elements is due to the ability of nuclei to possess multiple electric charge. Furthermore, the energy involved in almost all natural processes can be traced to nuclear reactions and transformations. In the following sections we will study about the nucleus and phenomenon associated with nucleus.
The atomic nucleus consists of two types of elementary particles, viz. Protons and neutrons. These particles are called nucleons.
The proton (denoted by p) has a charge +e and a mass
\displaystyle {{m}_{p}}\approx 1.6726\times {{10}^{{-27}}}kg, which is approximately 1840 times larger than the electron mass. The proton is the nucleus of the simplest atom with Z = 1, viz. the hydrogen atom.
The neutron (denoted by n) is an electrically neutral particle (its charge is zero). The neutron mass \displaystyle {{m}_{p}}\approx 1.6749\times {{10}^{{-27}}}kg. The fact that the neutron mass exceeds the proton mass by about 2.5 electron masses is of essential importance. It follows from this that the neutron in free state (outside the nucleus) is unstable (radioactive). During the time equal on the average to 12 min, the neutron spontaneously transforms to the proton by emitting an electron (e–) and a particle called the antineutrino ( \bar{v}). This process can be schematically written as follows:
n ® p + {{e}^{-}} +\bar{v}.
The most important characteristics of the nucleus are the charge number
Z (coinciding with the atomic number of the element) and the mass number A. The charge number Z is equal to the number of protons in the nucleus, and hence it determines the nuclear charge equal to Ze. The mass number A is equal to the number of nucleons in the nucleus (i.e. to the total number of protons and neutrons).
Nuclei are symbolically designated as
X_{Z}^{A} or \displaystyle _{Z}{{X}^{A}}
where X stands for the symbol of a chemical element. For example, the nucleus of the oxygen atom is symbolically written as O_{8}^{{18}} or \displaystyle _{8}{{O}^{{18}}}.
Nuclear characteristics
(i) Nuclear mass: It was observed in Rutherford’s \alphaa-particle scattering experiment that mass of an atom is concentrated within a very small positively charged region at the centre called nucleus. The total mass of nucleons in the nucleus is called as nuclear mass.
Nuclear mass = mass of protons + mass of neutrons
(ii) Nuclear charge: Nucleus is made of protons and neutrons. Protons have positive charge of magnitude equal to that of electron and neutrons are uncharged. So, nuclear charge = Ze
(iii) Size and shape of the nucleus: The nucleus is nearly spherical. Hence its size is usually given in terms of radius. The radius of nucleus was measured by Rutherford and it was found to have following relation \displaystyle R={{R}_{0}}{{A}^{{1/3}}}
where \displaystyle {{R}_{0}}=\text{ }1.1fm=\text{ }1.1\times {{10}^{{-15}}} m and A is mass number of particular element.
(iv) Nuclear density: The ratio of the mass of the nucleus to its volume is called nuclear density. As the masses of proton and neutron are roughly equal, the mass of a nucleus is roughly proportional to A.
As volume of a nucleus is V=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi R_{0}^{3}A
\displaystyle V\propto A
Thus, the density within a nucleus is independent of A.
Different types of nuclei
There are different types of nuclei depending upon the number of protons or the total number of nucleons in them.
(i) Isotopes: The atoms of an element having same atomic number but different mass number are called isotopes of that element i.e. different isotopes of the same element have same number of protons inside the nucleus but different number of neutrons inside the nucleus. Though isotopes have same chemical properties but their nuclear properties are highly different. Examples of isotopes are \displaystyle _{1}{{H}^{1}}{{,}_{1}}{{H}^{2}}{{,}_{1}}{{H}^{3}}an{{d}_{8}}{{O}^{{16}}}{{,}_{8}}{{O}^{{17}}}{{,}_{8}}{{O}^{{18}}} etc.
(ii) Isotones: Atoms whose nuclei have same number of neutrons are called isotones. For them, both the atomic number Z and atomic mass A are different but the value of difference (A – Z) is same. Examples of isotones are \displaystyle _{1}{{H}^{3}}{{,}_{2}}H{{e}^{4}}{{,}_{1}}{{H}^{2}},\text{ }and{{\text{ }}_{2}}H{{e}^{3}}etc.
(iii)Isobars: Atoms of same mass number but different atomic number are called isobars examples of isobars are \displaystyle _{1}{{H}^{3}}\text{ }and{{\text{ }}_{2}}H{{e}^{3}}{{,}_{6}}{{C}^{{14}}}\text{ }and{{\text{ }}_{7}}{{N}^{{14}}}etc
Atomic mass unit
Atomic masses are specified in terms of the atomic mass unit or unified mass unit (u). The mass of a neutral atom of the carbon isotope \displaystyle _{6}{{C}^{{12}}} is defined to be exactly 12 u.
Hence 1a.m.u. is defined as 1/12 of the mass of an unbound neutral atom of carbon-12 in its nuclear and electronic ground state and at rest.
\displaystyle 1u=1.66056\times {{10}^{{-27}}}kg
Einstein’s mass energy equivalence relations
Einstein on the basis of theory of relativity showed that mass of a body is not independent of energy but they are inter convertible. According to Einstein if a substance loses an amount \displaystyle \Delta m of its mass, an equivalent amount \displaystyle \Delta E of energy is produced, such that \displaystyle \begin{array}{l}\Delta E=\text{ }(\Delta m){{c}^{2}}\\{{R}_{0}}=\text{ }1.1fm=\text{ }1.1\times {{10}^{{-15}}},V\propto A{{,}_{6}}{{C}^{{12}}}\end{array} where c is the speed of light. This is called Einstein’s mass-energy equivalence relation.
Energy equivalent to 1u
If we put m= \displaystyle 1u=1.66056\times {{10}^{{-27}}}kg and \displaystyle c=3\times {{10}^{8}}m/sec, in the Einstein’s mass-energy equivalence relation \displaystyle E=m{{c}^{2}}.
we have \displaystyle E=1.66056\times {{10}^{{-27}}}\times {{\left( {3\times {{{10}}^{8}}} \right)}^{2}}\text{ = 1}\text{.5}\times \text{1}{{\text{0}}^{{-10\text{ }}}}\text{Joule}
As this energy is very small so it is better to convert it into a smaller unit. This smaller unit is electron volt or eV.
Hence \displaystyle E=\frac{{\text{1}\text{.5}\times \text{1}{{\text{0}}^{{-10\text{ }}}}}}{{1.6\times {{{10}}^{{-19}}}}}\text{ eV = 937}\text{.5 MeV}
If we put the values of m and c with greater accuracy the energy comes out to be around 931.5 MeV.
Hence 1u = 931.5MeV
Presenting mass of particles in terms of energy
In nuclear physics mass is usually represented in terms of energy according to the conversion formula \displaystyle E=m{{c}^{2}}.
For example the mass of an electron is \displaystyle 9.1\times {{10}^{{-31}}} kg. When this mass is converted into energy according to \displaystyle E=m{{c}^{2}}
we get \displaystyle E=9.1\times {{10}^{{-31}}}\times {{\left( {3\times {{{10}}^{8}}} \right)}^{2}}\text{ = 8}\text{.19}\times \text{1}{{\text{0}}^{{-14\text{ }}}}\text{Joule}
In eV this energy is \displaystyle E=\frac{{\text{8}\text{.19}\times \text{1}{{\text{0}}^{{-14\text{ }}}}}}{{1.6\times {{{10}}^{{-19}}}}}\text{ =511875 eV = 511}\text{.8 keV}
now if we put it back in \displaystyle E=m{{c}^{2}} and finding m
we get \displaystyle m=\frac{E}{{{{c}^{2}}}}\text{ = }\frac{{\text{511}\text{.8}}}{{{{c}^{2}}}}\text{ keV}
now we can write the mass of electron in terms of energy as \displaystyle 511.8\text{ }KeV/{{c}^{2}}.
Note that If we put the values with greater accuracy the final answer comes out to be around \displaystyle 511\text{ }KeV/{{c}^{2}}.
Similarly, the mass of a proton is \displaystyle 938\text{ }MeV/{{c}^{2}} (try to calculate yourself)
Nuclear Forces
The strong forces of attraction, which firmly hold the nucleons in the nucleus, are known as nuclear forces. Though the exact theory of nuclear forces is still to be understood completely, yet it is undoubtedly established that these forces exist between the nucleons i.e. between a neutron and a proton, between two proton and between two neutrons. The stability of nucleus is due to the presence of these forces. Nuclear forces have following important characteristics.
- Nuclear forces are short ranged, effective only up to a distance of the order of a ferometer or less and becomes negligible at separations more than 10 fm.
(ii) Nuclear forces are much stronger than electromagnetic forces in the nuclear range.
(iii) Nuclear forces are independent of charge.
(iv) The force between a pair of nucleons in not solely determined by the distance between the nucleons but also depends on the directions of the spin of the nucleons. The force is stronger if the spins of the nucleons are parallel and is weaker if the spins are antiparallel.
Mass Defect
A nucleus is made when various nucleons come together . It has been observed experimentally that the mass of the nucleus formed is always less than the sum of the masses of its constituent nucleons when measured in free state.
This difference between the total mass of the nucleons and the mass of the nucleus formed is called the mass defect of the nucleus (denoted by Dm)
Let the mass of one proton = \displaystyle {{m}_{p}},
Let the mass of one neutron = \displaystyle {{m}_{n}},
Let atomic number / no. of protons = Z
Let mass number / total no. of nucleons = A
Total mass of protons = no. of protons x mass of one proton = Z. \displaystyle {{m}_{p}}
Total mass of neutrons = no. of neutrons x mass of one neutron = (A-Z) \displaystyle {{m}_{n}},
Total mass of nucleons = Total mass of protons + Total mass of neutrons = Z. \displaystyle {{m}_{p}} + (A-Z) \displaystyle {{m}_{n}}
Let mass of nucleus formed = \displaystyle {{m}_{nuc}},
then mass defect is given as \displaystyle \Delta m=\text{ }[Z{{m}_{p}}+\text{ }(A-Z){{m}_{n}}]-{{m}_{{nuc}}}. Where this difference of mass has gone?
BINDING ENERGY OF NUCLEUS
It is defined as the total energy required to liberate all the nucleons from the nucleus in other words it is the energy required to disintegrate the nucleus completely into its constituent particles and placing them at infinity.
Clearly, this is the same energy with which the nucleons are held together within the nucleus. The origin of binding energy results from strong nuclear exchange forces.
Now from where this energy comes?
Answer is that the mass defect provides this energy. Actually the decrease in mass has been converted into energy binding the nucleons together according to the following relation: \displaystyle \Delta E=\text{ }(\Delta m){{c}^{2}}
where \displaystyle \Delta E = binding energy of nucleus, \displaystyle \Delta m = decrease in mass or mass defect) and
c = speed of light.
Hence in the formation of stable nucleus, the following equation holds good.
Mass of protons + Mass of neutrons = Mass of nucleus + Binding energy
Let’s see an example:
Consider a deuteron ( \displaystyle _{1}{{H}^{2}}) nucleus. It is the nucleus of heavy hydrogen or deuterium ( \displaystyle _{1}{{H}^{2}}). It contains 1 proton and 1 neutron. We shall compare the mass of one free proton and one free neutron with their mass when combined to form deuteron and thus find out mass defect and binding energy of deuteron.
Mass one free neutron = \displaystyle 1.675\times {{10}^{{-27}}} kg = 1.008665 u
Mass of one free proton = \displaystyle 1.673\times {{10}^{{-27}}} kg = 1.007825 u.
Their total = \displaystyle 3.348\times {{10}^{{-27}}}kg = 2.01649 u.
Mass of deuteron = \displaystyle 3.344\times {{10}^{{-27}}}kg = 2.014103 u.
\ Mass defect \displaystyle \Delta m = 0.002387 u.
It shows that when a proton and a neutron come together to form a deuteron, a small mass of 0.002387u disappears. In fact, this mass is converted into binding energy according to the following relation:
\Delta E=\Delta m{{c}^{2}}=\frac{{0.002387\times 1.66\times {{{10}}^{{-27}}}\times {{{(3\times {{{10}}^{8}})}}^{2}}}}{{1.6\times {{{10}}^{{-19}}}}}=2.22\times {{10}^{6}}\,\text{eV}=2.22\ \text{MeV}
Binding energy curve
A graph between the binding energy per nucleon and the mass number of nuclei is called the binding energy curve.
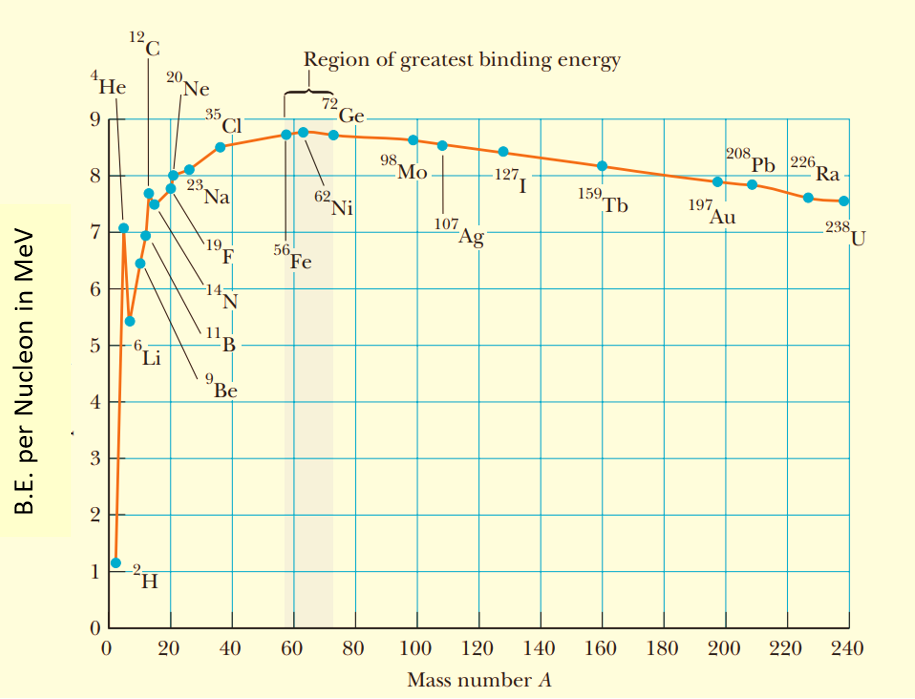
The following points may be noted from the binding energy curve:
(a) The binding energy per nucleon is maximum ( \displaystyle \approx 8.8 MeV) for the nucleus having mass number 56. So, this nucleus is most stable i.e. iron is the most stable element of periodic table.
(b) The light nuclei with A < 20 are least stable.
(c) The curve has certain peaks indicating that certain nuclei like _{\mathbf{2}}^{\mathbf{4}}\mathbf{He}\ \mathbf{,}\ _{\mathbf{6}}^{{\mathbf{12}}}\mathbf{C} and _{8}^{{16}}O are much more stable than the nuclei in their vicinity. It is due to the nature of the nuclear forces that they favor pairing of neutron and proton. Means they are more strong if there are equal number of neutrons and protons in the nucleus.
(d) For atomic number Z > 56, the curve takes a downside turn indicating lesser stability of these nuclei.
This is because of two reasons
- As the atomic number increases the number of protons and hence their mutual electrostatic force of repulsion increases which tends to make the nucleus unstable.
- Due to large size of nucleus, nuclear forces are not able to hold all the nucleons together because of its short range nature. Whereas the electrostatic force of repulsion among the protons is long range and dominates over nuclear force
(e) Nuclei of intermediate mass are most stable. This means maximum energy is needed to break them into their nucleons.
(f) The binding energy per nucleon has a low value for both very light and very heavy nuclei. Hence, if we break a very heavy nucleus (like uranium) into comparatively lighter nuclei then the binding energy per nucleon will increase. Hence a large quantity of energy will be liberated in this process. This phenomenon is called nuclear fission.
(g) Similarly, if we combine two or more very light nuclei (e.g. nucleus of heavy hydrogen \displaystyle _{1}H{{e}^{2}}) into a relatively heavier nucleus (e.g. \displaystyle _{2}H{{e}^{4}}), then also the binding energy per nucleon will increase i.e., again energy will be liberated. This phenomenon is called nuclear fusion.
Calculation for binding energy per nucleon:
In order to compare the stability of various nuclei, we calculate binding energy per nucleon. Higher is the binding energy per nucleon more stable is the nucleus.
We have seen that the mass defect during the formation of a nucleus:
\displaystyle \Delta m=\text{ }[Z{{m}_{p}}+\text{ }(A-Z){{m}_{n}}]-m, where \displaystyle {{m}_{p}}, \displaystyle {{m}_{n}}and m are masses of proton, neutron and nucleus respectively.
\ Total binding energy of nucleus \displaystyle \Delta E=\text{ }(\Delta m){{c}^{2}}
hence \displaystyle \Delta m=\text{ }\!\!\{\!\!\text{ (}Z{{m}_{p}}+\text{ }(A-Z){{m}_{n}})-{{m}_{{nuc}}}\}\times {{c}^{2}}
\ Mean binding energy per nucleon = \frac{{\Delta E}}{A}=\frac{{\Delta m{{c}^{2}}}}{A}=\left[ {\frac{Z}{A}\ ({{m}_{p}}-{{m}_{n}})+{{m}_{n}}-\frac{m}{A}} \right]\times {{c}^{2}}
If the mass m of the nuclease is found experimentally, we can find mean binding energy per nucleon since all other factors are known to us.
Calculation of Q value in a Nuclear Reaction
Consider a case where a particle `a’ moving with kinetic energy \displaystyle {{K}_{1}} is bombarded on nucleus `X’ moving with kinetic energy \displaystyle {{K}_{2}}. As a result of bombardment new particles `b’ and `Y’ are formed

So Initial energy is \displaystyle {{E}_{i}} which is the sum of rest mass energies ( \displaystyle m{{c}^{2}}) and kinetic energies of `a’ and `X’
\displaystyle {{E}_{i}}=\text{ }={{m}_{1}}{{c}^{2}}+{{m}_{2}}{{c}^{2}}+{{K}_{1}}+{{K}_{{2}}}
similarly Final energy:
\displaystyle {{E}_{f}}={{m}_{3}}{{c}^{2}}+{{m}_{4}}{{c}^{2}}+{{K}_{3}}+{{K}_{4}}
Since \displaystyle {{E}_{i}}={{E}_{f}} (energy conservation)
hence \displaystyle {{m}_{1}}{{c}^{2}}+{{m}_{2}}{{c}^{2}}+{{K}_{1}}+{{K}_{{2}}}={{m}_{3}}{{c}^{2}}+{{m}_{4}}{{c}^{2}}+{{K}_{3}}+{{K}_{4}}
\ \displaystyle \left[ {\left( {{{m}_{1}}+{{m}_{2}}} \right)\text{ }-\text{ }\left( {{{m}_{3}}+{{m}_{4}}} \right)} \right]{{c}^{2}}=\text{ }\left( {{{K}_{3}}+{{K}_{4}}} \right)\text{ }-\text{ }\left( {{{K}_{1}}+{{K}_{2}}} \right)~….(1)
here \displaystyle {{m}_{1}}+\text{ }{{m}_{2}} is the total mass of the reactant and \displaystyle {{m}_{3}}+\text{ }{{m}_{4}} is the total mass of the product
therefore \displaystyle \left( {{{m}_{1}}+{{m}_{2}}} \right)\text{ }-\text{ }\left( {{{m}_{3}}+{{m}_{4}}} \right) is the mass defect of the reaction and this difference of mass is converted into energy.
So L.H.S. of equation (1) represents the energy released or absorbed during nuclear reaction
This energy, that is released or absorbed in a nuclear reaction is called the Q – value or disintegration energy of the reaction.
hence \displaystyle Q=\left[ {\left( {{{m}_{1}}+{{m}_{2}}} \right)\text{ }-\text{ }\left( {{{m}_{3}}+{{m}_{4}}} \right)} \right]{{c}^{2}}J [ If masses are in kg]
or \displaystyle Q=[\left( {{{m}_{1}}+{{m}_{2}}} \right)\text{ }-\text{ }\left( {{{m}_{3}}+{{m}_{4}}} \right)~]~\times 931.5MeV [ If masses are in amu]
If Q is positive, rest mass energy is converted to kinetic mass energy, radiation mass energy or both, and the reaction is exoergic.
If Q is negative, the reaction is endoergic. The minimum amount of energy that a bombarding particle must have in order to initiate an endoergic reaction, is called Threshold Energy {{E}_{th}} .
<strong><em>{{E}_{th}}=-Q</em></strong>\left( {\frac{{{{m}_{1}}}}{{{{m}_{2}}}}+1} \right)
where {{m}_{1}} = mass of the projectile
{{m}_{2}} = mass of the target
Nuclear fission
The phenomenon of breaking a heavy nucleus into two light nuclei of almost equal masses along with the release of huge amount of energy is called nuclear fission. The process of nuclear fission was first discovered by German Scientists Otto Hahn and Strassman is 1939. They bombarded uranium nucleus ( \displaystyle _{{92}}{{U}^{{235}}}) with slow neutrons and found that \displaystyle _{{92}}{{U}^{{236}}} was split into two medium weight parts with the release of enormous energy. These fragments has atomic numbers far less than the target nucleus ( \displaystyle _{{92}}{{U}^{{235}}}). The nuclear fission of \displaystyle _{{92}}{{U}^{{235}}} is given by the following nuclear reaction:
\displaystyle _{{92}}{{U}^{{235}}}{{+}_{0}}{{n}^{1}}~\to ~\left[ {_{{92}}{{U}^{{236}}}} \right]~{{\to }_{{56}}}B{{a}^{{144}}}{{+}_{{36}}}K{{r}^{{89}}}+\text{ }{{3}_{0}}{{n}^{1}}+\text{ }energy.
The fission of \displaystyle _{{92}}{{U}^{{235}}} nucleus when bombarded with a neutron takes place in following manner. When a neutron strikes \displaystyle _{{92}}{{U}^{{235}}} nucleus, it is absorbed by it, producing a highly unstable \displaystyle _{{92}}{{U}^{{236}}} nucleus. Instead of emitting \alpha or \beta particles or \gamma rays, this unstable nucleus is split into two middle weight parts viz \displaystyle _{{56}}{{Ba}^{{144}}} and krypton ( \displaystyle _{{36}}{{Kr}^{{89}}}). During this fission, three neutrons are given out and a small mass defect occurs which is converted into enormous amount of energy.
The following points are worth noting about nuclear fission process:
(a) The energy released in the fission of uranium is about 200 MeV per nucleus. This can be easily verified. If we obtain atomic mass unit values of reactants and products in the fission of \displaystyle _{{92}}{{U}^{{235}}} nucleus, we find that there occurs a mass defect of 0.214u. Which is converted into energy. Energy released per fission of \displaystyle _{{92}}{{U}^{{235}}} nucleus is equal to 0.214 ´ 931 \displaystyle \approx 200 MeV
(b) The products of uranium fission are not always barium and krypton. Sometimes, they are Strontium and Xenon. There are other pairs as well. However, in each case, neutrons are emitted and tremendous amount of energy is released.
(c) Energy is released in the form of kinetic energy of fission fragments. Some of the energy is also released in the form of \gamma-rays, heat energy sound energy and light energy.
(d) The pressure and temperature is very high in fission process.
Nuclear Fusion
The process of combining two light nuclei to form a heavy nucleus is known as nuclear fusion. An important feature of nuclear fusion is that there is a release of huge amount of energy in the process. This can be easily understood. When two light nuclei are combined to form a heavy nucleus there occurs a small mass defect. This small mass defect results in the release of huge amount of energy according to the relation \displaystyle \Delta E=m{{c}^{2}}. For example by the fusion of two nuclei of heavy hydrogen, the following reaction is possible.
\displaystyle _{1}{{H}^{2}}{{+}_{1}}{{H}^{2}}{{\to }_{1}}{{H}^{3}}{{+}_{1}}{{H}^{1}}+\Delta {{E}_{1}}
The nucleus of tritium _{1}^{3}H so formed can again fuse with a deuterium nucleus.
_{\mathbf{1}}^{\mathbf{3}}\mathbf{H}+_{\mathbf{1}}^{\mathbf{2}}\mathbf{H}\xrightarrow{{}}_{\mathbf{2}}^{\mathbf{4}}\mathbf{He}+_{\mathbf{0}}^{\mathbf{1}}\mathbf{n}+\mathbf{\Delta }{{\mathbf{E}}_{\mathbf{2}}}
Nuclear fusion is a very difficult process to achieve. This is because when positively charged nuclei come close to each other for fusion they required very high energy to counter repulsive force between them. So a high temperature is required for fusion. Though the energy output in the process of nuclear fission seems to be much more than in a nuclear fusion, but actually the energy liberated by the fusion of a certain mass of heavy hydrogen is much more than the energy liberated by the fission of equal mass of uranium. In other words for equal mass of reactants the energy liberated in fusion is much more than the energy liberated in fission.
Illustration
In nuclear reaction, there is conservation of
(1) mass only
(2) energy only
(3) momentum only
(4) mass, energy and momentum
Solution:
Mass, energy and momentum are conserved.
\ (4)
Illustration
Taking 1u = 931 MeV, calculate the mass of \displaystyle _{6}{{C}^{{12}}} atom.
Solution:
\displaystyle 1u\text{ }=\text{ }931\text{ }MeV\text{ }=\text{ }931\text{ }\times \text{ }1.602\text{ }\times {{10}^{{3}}}J
As E=m{{c}^{2}} or m=\frac{E}{{{{c}^{2}}}}
\ 1\,\text{u}=\frac{{931\times 1.602\times {{{10}}^{{-13}}}}}{{{{{(3\times {{{10}}^{8}})}}^{2}}}}=1.657\times {{10}^{{-27}}}\text{kg}
Mass of nothing \displaystyle _{6}{{C}^{{12}}} atom = 12 u = \displaystyle 12\text{ }\times \text{ }1.657\text{ }\times \text{ }{{10}^{{27}}}
Illustration
Obtain approximately the ratio of nuclear radius of the gold isotope \displaystyle _{79}{{Au}^{{197}}} and the silver isotope \displaystyle _{47}{{Ag}^{{107}}} . What is the approximate ratio of their nuclear mass densities?
Solution:
As R={{R}_{0}}{{A}^{{1/3}}}
\ \frac{{R(\mathbf{A}{{\mathbf{u}}^{{179}}})}}{{R(\mathbf{A}{{\mathbf{g}}^{{107}}})}}={{\left( {\frac{{179}}{{107}}} \right)}^{{1/3}}}=1.23
Now nuclear mass density is constant for all nuclei, therefore, \frac{{\rho (\mathbf{A}{{\mathbf{u}}^{{179}}})}}{{\rho (\mathbf{A}{{\mathbf{g}}^{{107}}})}}=1.
Illustration
Calculate the binding energy per nucleon (B.E./nucleon) in the nuclei of \displaystyle _{26}{{Fe}^{{56}}} .
Given: m ( \displaystyle _{26}{{Fe}^{{56}}}) = 55.934939 u,
\displaystyle m\left[ {_{0}{{n}^{1}}} \right]\text{ }=\text{ }1.00865\text{ }u,
\displaystyle m\left[ {_{1}{{H}^{1}}} \right]\text{ }=\text{ }1.00782\text{ }u .
Solution:
The \displaystyle _{26}{{Fe}^{{56}}} nucleus has 26 protons and 30 neutrons.
Mass of 26 protons = 26 × 1.00782 = 26.20332 u
Mass of 30 neutron = 30 × 1.00865 = 30.25950 u
Total mass = 56.46282 u
Mass of \displaystyle _{26}{{Fe}^{{56}}} nucleus = 55.934939 u
Mass defect, \displaystyle \Delta m = 0.527881 u
B.E. of \displaystyle _{26}{{Fe}^{{56}}} nucleus = \Delta m\times 931\,\text{MeV}=0.527881\times 931=491.457\text{MeV}
B.E./nucleon =\frac{{491.457}}{{56}}=8.776\,\text{MeV}.
Illustration
Calculate the energy released by the fission of 1g of \displaystyle _{92}{{U}^{{235}}} in kWh. Energy released per fission is 200 MeV.
Solution:
Number of atoms in one 1g of \displaystyle _{92}{{U}^{{235}}} =\frac{{\text{Avogadro }\!\!’\!\!\text{ s}\ \text{number}}}{{\text{Mass}\ \text{number}}}=\frac{{6.023\times {{{10}}^{{23}}}}}{{235}}
Energy released per fission = 200 MeV
Energy released by fission of 1 g of \displaystyle _{92}{{U}^{{235}}}
=\frac{{6.023\times {{{10}}^{{23}}}\times 200}}{{235}}\text{MeV}=5.126\times {{10}^{{23}}}\text{MeV}
=5.126\times {{10}^{{23}}}\times 1.6\times {{10}^{{-13}}}\text{J}=\frac{{5.126\times 1.6\times {{{10}}^{{10}}}}}{{3.6\times {{{10}}^{6}}}}\text{kWh} =2.278\times {{10}^{4}}\text{kWh}.
Illustration
Two deuterium nuclei fuse to form a tritium nucleus and a proton as by product. Compute the energy released.
Given: Mass of deuterium = 2.0141 u
Mass of tritium nucleus = 3.01605 u
and mass of proton = 1.00782u
Solution:
_{\mathbf{1}}^{\mathbf{2}}\mathbf{H}\,+\,_{\mathbf{1}}^{\mathbf{2}}\mathbf{H}\,¾® _{\mathbf{1}}^{\mathbf{3}}\mathbf{H}\,+\,_{\mathbf{1}}^{\mathbf{1}}\mathbf{H}\,+\,\mathbf{\Delta E}
Mass of reactants = 2.0141 × 2 = 4.02820 u
Mass of products = 3.01605 + 1.00782 = 4.02387 u
Mass defect = 4.0282 – 4.02387 = 0.00433 u
Energy released = 0.00433 × 931 = 4.03 MeV.
Illustration
A star initially has \displaystyle {{10}^{{40}}} deuterons. It produces energy via the processes
\displaystyle _{1}{{H}^{2}}{{+}_{1}}{{H}^{2}}\to {{~}_{1}}{{H}^{3}}+\text{ }p and \displaystyle _{1}{{H}^{2}}{{+}_{1}}{{H}^{3}}\to {{~}_{2}}{{He}^{4}}+\text{ }n .
If the average power radiated by the star is \displaystyle {{10}^{{16}}} W, the deuteron supply of the star is exhausted in a time of the order of [The masses of nuclei are: m({{H}^{2}} = 2.014 u, m(p) = 1.007 u, m(n) = 1.008 u, m({{He}^{4}}) = 4.001 u]
(a) \displaystyle {{10}^{{6}}} s
(b) \displaystyle {{10}^{{8}}} s
(c) \displaystyle {{10}^{{12}}} s
(d) \displaystyle {{10}^{{16}}} s
Solution:
\displaystyle \Delta m = 0.026 amu
{{Q}_{value}} = 2.42 MeV
t = 1.28\times {{10}^{{12}}}s
\ (c)
Illustration
When \displaystyle _{3}{{Li}^{7}} nuclei are bombarded by protons, and the resultant nuclei are \displaystyle _{4}{{Be}^{8}} , the emitted particles will be
(a) neutrons (b) alpha particles
(c) beta particles (d) gamma photons
Solution:
Gamma-photon
\ (d)
Illustration
A neutron breaks into a proton and electron. Calculate the energy produced in this reaction in MeV. Mass of an electron = \displaystyle 9\times {{10}^{{-31}}} kg, Mass of proton = \displaystyle 1.6725\text{ }\times \text{ }{{10}^{{-27}}}kg, Mass of neutron \displaystyle 1.6747\text{ }\times \text{ }{{10}^{{-27}}} kg. Speed of light = \displaystyle 3\text{ }\times \text{ }{{10}^{{8}}} m/s.
Solution:
\displaystyle _{o}{{n}^{1}}{{\to }_{1}}{{H}^{1}}{{+}_{{-1}}}{{e}^{o}}
Mass defect ( \displaystyle \Delta m) = [Mass of neutron – (mass of proton + mass of electron)]
= \displaystyle 1.6747\times {{10}^{{-27}}}\text{ }(1.6725\times {{10}^{{-27}}}+\text{ }9\times {{10}^{{-31}}})
= \displaystyle 0.0013\times {{10}^{{-27}}} kg
\ Energy released \displaystyle Q=\text{ }(\Delta m){{c}^{2}}
\displaystyle Q=\text{ }(0.0013\times {{10}^{{-27}}})\times {{(3\times {{10}^{8}})}^{2}}=\text{ }1.17\times {{10}^{{-13}}}J
= \frac{{1.17\times {{{10}}^{{-13}}}}}{{1.6\times {{{10}}^{{-19}}}}} = \displaystyle 0.73\times {{10}^{6}}eV = 0.73 MeV
Illustration
Neon – 23 beta decays in the following way :
_{{10}}^{{23}}Ne\to _{{11}}^{{23}}Na+_{{-1}}^{o}e+\bar{\nu }
Find the minimum and maximum kinetic energy that the beta particle _{{-1}}^{o}e can have. The atomic masses of \displaystyle ^{{23}}Ne and \displaystyle ^{{23}}Na are 22.9945 u and 22.9898 u, respectively.
Solution:
Reactant Products
_{{10}}^{{23}}Ne 22.9945 – 10 \displaystyle {{m}_{e}} \displaystyle _{{11}}^{{23}}Na 22.9898 – 11 \displaystyle {{m}_{e}}
\displaystyle _{{-1}}^{o}e –me
Total 22.9945 – 10 \displaystyle {{m}_{e}} Total 22.9898 – 10 \displaystyle {{m}_{e}}
Mass defect = 22.9945 – 22.9898 = 0.0047 u
Q = (0.0047)(931) = 4.4 MeV
The \beta – particle and neutrino share this energy. Hence the energy of the \beta-particle can range from 0 to 4.4 MeV.
Illustration
How much energy must a bombarding proton possess to cause the reaction.
\displaystyle _{3}^{7}Li+_{1}^{1}H\to _{4}^{7}Be+_{0}^{1}n
Given atomic mass of
_{3}^{7}Li 7.01600 u , \displaystyle _{4}^{7}Be 7.01693 u
_{1}^{1}H 1.0783 u , _{o}^{1}n 1.0866 u
Solution:
Since the mass of an atom include the masses of the atomic electrons, the appropriate number of electron masses must be subtracted from the given values.
Reactants Products
_{3}^{7}Li 7.01600 – 3 \displaystyle {{m}_{e}} \displaystyle _{4}^{7}Be 7.01693 – 4 \displaystyle {{m}_{e}}
_{1}^{1}H 1.0783 – 1 \displaystyle {{m}_{e}} _{o}^{1}n 1.0866
Total 8.02383 – 4 \displaystyle {{m}_{e}} Total 8.02559 – 4 \displaystyle {{m}_{e}}
The Q-value of the reaction
Q = -0.00176 u = -1.65 MeV
The energy is supplied as kinetic energy of the bombarding proton. The incident proton must have more than this energy because the system must possess some kinetic energy even after the reaction, so that momentum is conserved.
With momentum conservation taken into account, the minimum kinetic energy that the incident particle can be found with the formula.
{{E}_{th}}= – \left( {1+\frac{m}{M}} \right)Q=-\left( {1+\frac{1}{7}} \right)\left( {-1.65} \right)=1.89 MeV
Illustration
In a nuclear reactor, fission is produced in 1 g for {{U}^{235}} (235.0439 u) in 24 hours by a slow neutron (1.0087 u). Assume that _{35}{{Kr}^{92}} 35Kr92 (91.8973 u) and \displaystyle _{{56}}B{{a}^{{141}}} (140.9139 amu) are produced in all reactions and no energy is lost.
(a) Write the complete reaction
(b) Calculate the total energy produced in kilowatt hour. Given 1 u = 931 MeV.
Solution:
The nuclear fission reaction is \displaystyle _{{92}}{{U}^{{235}}}{{+}_{0}}{{n}^{1}}~\to ~_{{56}}}B{{a}^{{141}}}{{+}_{{36}}}K{{r}^{{92}}}+\text{ }{{3}_{0}}{{n}^{1}}
Mass defect \displaystyle \Delta m=\text{ }\left[ {\left( {{{m}_{u}}+{{m}_{n}}} \right)\text{ }\text{ }\left( {{{m}_{B}}_{a}+{{m}_{{Kr}}}+\text{ }3{{m}_{n}}} \right)} \right]
\displaystyle \Delta m = 256.0526 – 235.8373 = 0.2153 u
Energy released = 0.2153 ´ 931 = 200 MeV
Number of atoms in 1 g = \frac{{6.02\times {{{10}}^{{23}}}}}{{235}}=2.56 \times {{10}^{21}}
Energy released in fission of 1 g of \displaystyle {{{U}^{{235}}}} is
\displaystyle Q=\text{ }200\times 2.56\times {{10}^{{21}}}=\text{ }5.12\times {{10}^{{23}}}MeV
= \displaystyle (5.12\times {{10}^{{23}}})\times (1.6\times {{10}^{{-13}}})\text{ }=\text{ }8.2\times {{10}^{{10}}}J
= \frac{{8.2\times {{{10}}^{{10}}}}}{{3.6\times {{{10}}^{6}}}}kWh = \displaystyle 2.28\times {{10}^{4}} kWh
Illustration
It is proposed to use the nuclear fusion reaction:
\displaystyle _{1}{{H}^{2}}{{+}_{1}}{{H}^{2}}{{=}_{2}}H{{e}^{4}}
in a nuclear reactor of 200 MW rating. If the energy from above reaction is used with a 25% efficiency in the reactor, how many grams of deuterium will be needed per day. (The masses of \displaystyle _{1}{{H}^{2}} and \displaystyle _{2}H{{e}^{4}} are 2.0141 and 4.0026 u respectively).
Solution:
Energy released in the nuclear fusion is
\displaystyle Q=\Delta m{{c}^{2}}=\Delta m\left( {931} \right)MeV
Þ \displaystyle Q=\text{ }(2\times 2.0141\text{ }\text{ }4.0026)\times 931MeV\text{ }=\text{ }23.834\text{ }MeV\text{ }=\text{ }23.834\times {{10}^{6}}eV
Since efficiency of reactor is 25%
So effective energy used = \displaystyle 25\text{ }/\text{ }100\times 23.834\times {{10}^{6}}\times 1.6\times {{10}^{{-19}}}J\text{ }=\text{ }9.534\times {{10}^{{-13}}} J
Since the two deuterium nucleus are involved in a fusion reaction, therefore, energy released per deuterium is \frac{{9.534\times {{{10}}^{{-13}}}}}{2}
For 200MWpower per day
number of deuterium nuclei required = \frac{{200\times {{{10}}^{6}}\times 86400}}{{\frac{{9.534}}{2}\times {{{10}}^{{-13}}}}}=3.624 \times {{10}^{25}}
Since 2g of deuterium constitute \displaystyle 6\times {{10}^{{23}}} nuclei, therefore amount of deuterium required is
g = \frac{{2\times 3.624\times {{{10}}^{{25}}}}}{{6\times {{{10}}^{{23}}}}} = 120.83 g/day
Practice Questions (Basic Level)
1.
The nuclear radius of Pb208 is 8.874 fm. What will be the nuclear radius of Ca44?
(a) 5. 483fm
(b) 5.286 fm
(c) 0.146 fm
(d) 4.326 fm
Ans (b)
2.
The mass defect for the nucleus of helium is 0.0303u. What is the binding energy per nucleus for helium in MeV?
(a)28
(b)7
(c)4
(d)1.
Ans (b)
3.
If M is atomic mass, A is mass number, then \left( {\frac{{M-A}}{M}} \right) is called
(a)Binding energy
(b)Fermi energy
(c)Mass defect
(d)Packing fraction.
Ans (d)
4.
The more readily fissionable isotope of uranium has an atomic mass of
(a)238u
(b)236u
(c)235u
(d)234u.
Ans (c)
5.
Fusion reactions takes place at about
(a)3 × 102 K
(b)3 × 103 K
(c)3 × 104 K
(d)3 × 106 K.
Ans (d)
6.
The mass density of a nucleus varies with mass number A as
(a)A2
(b)A
(c)constant
(d)1/A
Ans (c)
7.
In nuclear fission, 0.1 % mass is converted into energy. The energy released by the fission of 1 kg mass is
(a)2.5 × 105 k Wh
(b)2.5 × 107 k Wh
(c)2.5 × 106 k Wh
(d)2.5 × 10–7 k Wh.
Ans (b)
8.
In a given nuclear reaction 2He4 + Z X _____ Z+2Y A + 3 + K, K is
(a) electron
(b) positron
(c) proton
(d) neutron
Ans (d)
9.
A nucleus with A = 235 splits into two nuclei whose mass numbers are in the ratio 2 : 1. If R0 = 1.4 fm, find the radii of the new nuclei.
(a) 5.99 fm, 1.45 fm
(b) 5.99 fm, 0.23 fm
(c) 5.99 fm, 8.36 fm
(d) 5.99 fm, 7.55 fm
Ans (d)
10.
Calculate the binding energy per nucleon for a 6C12 nucleus. Atomic mass of 6C12 = 12u, mass of a proton = 1.007825u, mass of a neutron = 1.008665u.
(a) 1.00 MeV
(b) 7.68 MeV
(c) 2.33 MeV
(d) 0.32 MeV
Ans (b)
11.
A nuclear reaction used U235 as fuel as an output of 106 W. How much uranium is consumed per hour? The energy released per fission is 200 MeV. Given Avogadro’s number = 6.023 × 1023 mol–1.
(a) 1.0354 g
(b) 0.025 g
(c) 0.0439 g
(d) 2.2339 g
Ans (c)
Practice Questions (JEE Main Level)
1.
Calculate the binding energy of a deutron. Given that
mass of proton = 1.007825u
mass of neutron = 1.008665u
mass of a deutron = 2.014103u.
(a) 2.2 MeV
(b) 3.94 MeV
(c) 2.44 MeV
(d) 0.3 MeV
Ans (a)
2.
If element with principal quantum number n> 4 were not allowed in nature, the number of possible elements would be
(a) 60
(b) 31
(c) 4
(d) 64.
Ans (a)
3.
In stable nuclei, the number of neutrons (N) is related to the number of electrons (Z) in the neutral atom in general as
(a) N > Z
(b) N = Z
(c) N < Z
(d) N ³ Z.
Ans (d)
4.
When a lithium nucleus (3Li7) is bombarded with certain particles, only two alpha particles are produced. The bombarding particles are
(a) photons
(b) electrons
(c) protons
(d) deutrons.
Ans (c)
5.
From the following equations pick out the possible nuclear fusion reactions
(a) _{\text{6}}{{\text{C}}^{{\text{13}}}}+{{\,}_{\text{1}}}{{\text{H}}^{\text{1}}}\to {{\,}_{\text{7}}}{{\text{N}}^{{\text{14}}}}+\text{4}\text{.3MeV}
(b) _{\text{6}}{{\text{C}}^{{\text{12}}}}+{{\,}_{\text{1}}}{{\text{H}}^{\text{1}}}\to {{\,}_{\text{7}}}{{\text{N}}^{{\text{13}}}}+\text{2}\,\text{MeV}
(c) _{\text{7}}{{\text{N}}^{{\text{14}}}}+{{\,}_{\text{1}}}{{\text{H}}^{\text{1}}}\to {{\,}_{\text{8}}}{{\text{O}}^{{\text{15}}}}+\text{7}.3\,\text{MeV}
(d) _{{\text{92}}}{{\text{U}}^{{\text{235}}}}+{{\,}_{\text{0}}}{{n}^{\text{1}}}\to {{\,}_{{\text{54}}}}\text{X}{{\text{e}}^{{\text{140}}}}+{{\,}_{{38}}}\text{S}{{\text{r}}^{{94}}} +2\,{{(}_{0}}{{n}^{1}})+\gamma +200\text{MeV}\text{.}
Ans (b)
6.
The mass number of He is 4 and that for sulphur is 32. The radius of sulphur nucleus is larger than that of helium by times
(a) \sqrt{8}
(b) 4
(c) 2
(d) 8.
Ans (c)
7.
M, Mn and Mp denote the masses of a nucleus ZXA, a neutron and proton respectively. If the nucleus is separated into its individual protons and neutrons then
(a) M=(A-Z){{M}_{n}}+Z{{M}_{p}}
(b) M=Z{{M}_{n}}+(A-Z){{M}_{p}}
(c) M>(A-Z){{M}_{n}}+Z{{M}_{p}}
(d) M<(A-Z){{M}_{n}}+Z{{M}_{p}}.
Ans (d)
8.
If all the atoms of 1 kg of deuterium undergo fusion, approximately how much energy could be released, if the fusion reaction is _{\text{1}}{{\text{H}}^{\text{2}}}+{{\,}_{\text{1}}}{{\text{H}}^{\text{2}}}\to {{\,}_{\text{2}}}\text{H}{{\text{e}}^{\text{3}}}+{{\,}_{\text{0}}}{{\text{n}}^{\text{1}}}+\text{3}\text{.8MeV}
(a)9 × 1013 J
(b)9 × 1011 calorie
(c)9 × 1012 kWh
(d)9 × 107 kWh.
Ans (a)
9.
Assuming that about 20 MeV of energy is released per fusion reaction _{\text{1}}{{\text{H}}^{\text{2}}}+{{\,}_{\text{1}}}{{\text{H}}^{\text{2}}}\to {{\,}_{\text{0}}}{{n}^{\text{1}}}+{{\,}_{\text{2}}}\text{H}{{\text{e}}^{\text{3}}} then the mass of 1H2 consumed per day in a fusion reactor of power 1 Megawatt will approximately be
(a) 0.001 gm
(b)0.1 gm
(c) 10.0 gm
(d) 1000 gm.
Ans (b)
10.
Given that mass of proton = 1.00813u, mass of neutron is 1.00894u and mass of
a-particle is 4.00388u, the binding energy of alpha particle is
(a) 28.172 MeV
(b) 27.172 MeV
(c) 13.52 MeV
(d) 56.321 MeV
Ans (a)
11.
Nuclear radius of 8O16 is 3 fermi. The nuclear radius of 82Pb205 is
(a) 5.02 fermi
(b) 6.02 fermi
(c) 7.02 fermi
(d) 8.02 fermi
Ans (c)
12.
Let mp be the mass of a proton, mn be the mass of a neutron, M1 be the mass of 10He20 nucleus and M2 the mass of 20Ca40 nucleus. Then
(a) M2 = 2M1
(b) M2> 2M1
(c) M2< 2M1
(d) M1< 10 (mp + mn)
Ans (d)
13.
If the nuclear force between two protons, two neutrons and between proton and neutron is denoted by Fpp, Fnn and Fpn respectively then
(a) Fpp = Fnp = Fnn
(b) Fpp¹Fnp but Fpp = Fnp
(c) Fpp = Fnn¹Fpn
(d) Fpp¹Fnn¹Fpn.
Ans (a)
14.
The binding energies per uncleon for a deutron and an a-particle are X1 and X2 respectively. What will be the energy Q released in the reaction? _{\text{1}}^{\text{2}}\text{H}+\,_{\text{1}}^{\text{2}}\text{H}\to \,_{\text{2}}^{\text{4}}\text{He}+\text{Q}
(a) 4 (X2 – X1)
(b) 2 (X2 – X1)
(c) 4 (X1 + X2)
(d) 2 (X1 + X2).
Ans (a)
15.
The real mass, MN of a stable nucleus differs from the total mass of its constituents (protons and neutrons) MT, in such a way that
(a) MN>MT
(b) MN is slightly smaller than MT
(c) MN = MT
(d) MN>>MT.
Ans (b)
16.
If the speed of light were \frac{2}{3} of its present value, the energy released in a given atomic explosion will be decreased by a fraction of
(a) \frac{2}{3}
(b) \frac{4}{9}
(c) \frac{5}{9}
(d) \frac{2}{9}.
Ans (b)
17.
The binding energy per nucleon of deutron and helium atom is 1.1 MeV and 7 MeV respectively. If two deutron atoms react to form a single helium, then the energy released is
(a) 13.9 MeV
(b) 26.9 MeV
(c) 23.6 MeV
(d) 19.2 MeV.
Ans (b)
18.
What is the power output of 92U235 reactor if it takes 30 days to use up 2 kg of fuel, and if each fission gives 185 MeV of usable energy? Avogadro’s number N = 6.02 ´ 1026 per kilomole.
(a) 50.65 MW
(b) 55.32 MW
(c) 57.00 MW
(d) 58.46 MW
Ans (d)
19.
Assuming all the energy released by the fission of each _{{92}}^{{235}}U nucleus (190 MeV) is absorbed by water, how many _{{92}}^{{235}}U atoms must undergo fission to warm 1 g of water by 1C°?
(a) 0.23 x 1011
(b) 1.87 x 1011
(c) 1.38 x 1011
(d) 5.83 x 1011
Ans (c)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
