Home

Theory For Notes Making

Practice Questions (Basic Level)

Practice Questions (Mains Level)

Practice Questions (Advance Level)

On Line Test (JEE Main Level)

On Line Test (JEE Advance Level)

Video Lecture

Theory For Making Notes

Radiation Pressure

Even though the rest mass of a photon is zero, it possess a linear momentum. When this photon falls on a surface it undergoes either reflection or absorption. During both the process there is a change in momentum of the photon and hence there exist a force.( Linear momentum cannot change without a force) Therefore whenever a radiation falls on a surface it experience a force and as a reaction it exert a force on the surface. The normal component of this force exerted per unit area of the surface is called the radiation pressure.

 

Momentum carried by photon

We know that wavelength of the radiations is given by

λ=hp \displaystyle \lambda =\frac{h}{p}     …(i)   where h is the Planck’s constant and p is the momentum of the photons.

Also we know that  energy `E’ of a photon is given as

E=hν \displaystyle E=h\nu     where frequency  ν=cλ \displaystyle \nu =\frac{c}{\lambda }

therefore E=hcλ \displaystyle E=\frac{{hc}}{\lambda }   …(ii)

putting λ\lambda  from equation (i) into equation (ii)

we get  E=hch/p   \displaystyle E=\frac{{hc}}{{{h}/{p}\;}}       

⇒E=pc \displaystyle \Rightarrow E=pc

hence p=Ec \displaystyle p=\frac{E}{c}  This is the momentum carried by photon of energy E

 

Intensity of radiations

It is the energy passing ( or falling) per unit area per unit time through ( or on) a surface placed perpendicular to the path of the radiations.

So  I=EA.Δt \displaystyle I=\frac{E}{{A.\Delta t}} , where E is energy , A is area placed perpendicular to the radiation and Δt \displaystyle \Delta t is time for which energy  passes  .

Also we know that EΔt=P  (Power) \displaystyle \frac{E}{{\Delta t}}=P\text{  (Power)}

Hence  I=PA \displaystyle I=\frac{P}{A} 

Calculation Of Radiation Pressure

CASE-1

When the radiations falls normally and fully (100%) absorbed by the surface

We know that the momentum carried by radiations is

p=Ec \displaystyle p=\frac{E}{c}                              … (iii)  ,

where E is the energy incident on the surface through radiation in time Δt \displaystyle \Delta t.

 

Also we have seen that the Intensity I is given by

I=EA.Δt \displaystyle I=\frac{E}{{A.\Delta t}}                            …(iv)

dividing (iii) by (iv) we get                        

pI=EcAΔtE \displaystyle \frac{p}{I}=\frac{E}{c}\frac{{A\Delta t}}{E}

⇒   p=IAΔtc \displaystyle \Rightarrow \text{   }p=\frac{{IA\Delta t}}{c}                             …(v)

(in the above equation p is the initial momentum carried by radiations which fall on the surface for time \Deltat\Deltat )

In case of 100% absorption of the radiations all this momentum becomes zero finally

hence final momentum p′{{p}^{\prime}}=0

so change in momentum in time Δt \displaystyle \Delta t is Δp \displaystyle \Delta p

where   Δp=p′−p=0 \displaystyle \Delta p={{p}^{\prime}}-p=0– IAΔtc \displaystyle \frac{{IA\Delta t}}{c}= –IAΔtc \displaystyle \frac{{IA\Delta t}}{c}

Hence ∣Δp∣=IAΔtc \displaystyle \left| {\Delta p} \right|\text{=}\frac{{IA\Delta t}}{c}

or  ∣ΔpΔt∣=IAc \displaystyle \left| {\frac{{\Delta p}}{{\Delta t}}} \right|\text{=}\frac{{IA}}{c}

or    F=IAc \displaystyle \text{F=}\frac{{IA}}{c}     ∵ ∣ΔpΔt∣ = F (magnitude of force) \displaystyle \because \text{ }\left| {\frac{{\Delta p}}{{\Delta t}}} \right|\text{ = F (magnitude of force)}

Here F is the force that developed due to change in momentum of the radiations as they are absorbed by the surface.

We can divide both sides by area `A’ we get  FA=Ic \displaystyle \frac{F}{A}\text{=}\frac{I}{c}

Hence Radiation Pressure P(radiation) \displaystyle {{P}_{{(radiation)}}} is given by  Pradiation=Ic \displaystyle {{\text{P}}_{{radiation}}}\text{=}\frac{I}{c}                         (∵ FA = Pressure) \displaystyle (\because \text{ }\frac{F}{A}\text{ = Pressure)}

CASE-2

When the radiations falls normally and fully reflected by the surface i.e. 100% reflection

 From equation no. (v) we can write the momentum of radiation before and after reflection

Initial momentum of radiations

 p=IAΔtc \displaystyle \text{ }p=\frac{{IA\Delta t}}{c} 

Final Momentum after reflection

 p’=−IAΔtc \displaystyle \text{ }p’=-\frac{{IA\Delta t}}{c}

so change in momentum is Δp \displaystyle \Delta p

where Δp=p′−p \displaystyle \Delta p={{p}^{\prime}}-p = −IAΔtc \displaystyle -\frac{{IA\Delta t}}{c}−IAΔtc \displaystyle -\frac{{IA\Delta t}}{c}= −2IAΔtc \displaystyle -\frac{{2IA\Delta t}}{c}

Hence ∣Δp∣=2IAΔtc \displaystyle \left| {\Delta p} \right|\text{=}\frac{{2IA\Delta t}}{c}

or   ∣ΔpΔt∣=2IAc \displaystyle \left| {\frac{{\Delta p}}{{\Delta t}}} \right|\text{=}\frac{{2IA}}{c}

or         F=2IAc \displaystyle \text{F=}\frac{{2IA}}{c}     ∵ ∣ΔpΔt∣ = F (magnitude of force) \displaystyle \because \text{ }\left| {\frac{{\Delta p}}{{\Delta t}}} \right|\text{ = F (magnitude of force)}

Here F is the force that developed due to change in momentum of the radiations as they are reflected by the surface.

We can divide both sides by area `A’ we get  FA=2Ic \displaystyle \frac{F}{A}\text{=}\frac{{2I}}{c}

Hence Radiation Pressure P(radiation) \displaystyle {{P}_{{(radiation)}}} is given by 

Pradiation=2Ic \displaystyle {{\text{P}}_{{radiation}}}\text{=}\frac{{2I}}{c}                       

(∵ FA = Pressure) \displaystyle (\because \text{ }\frac{F}{A}\text{ = Pressure)}

Note that Radiation pressure in case of 100% reflection is twice that in case of 100% absorption.

X-Rays

Production of X-rays

When highly energetic electrons are made to strike a metal target, electromagnetic radiations comes out. A large part of this radiations has wavelength of the order of 1Ao \displaystyle {{A}^{o}} and is called X-rays.

Soft and hard X-ray – The X-rays of low wavelengths are called hard X-rays and large wave lengths are called soft X-rays hard and soft are simply relative terms.

 The device which is used to produce X-rays is called Coolidge tube as shown below.

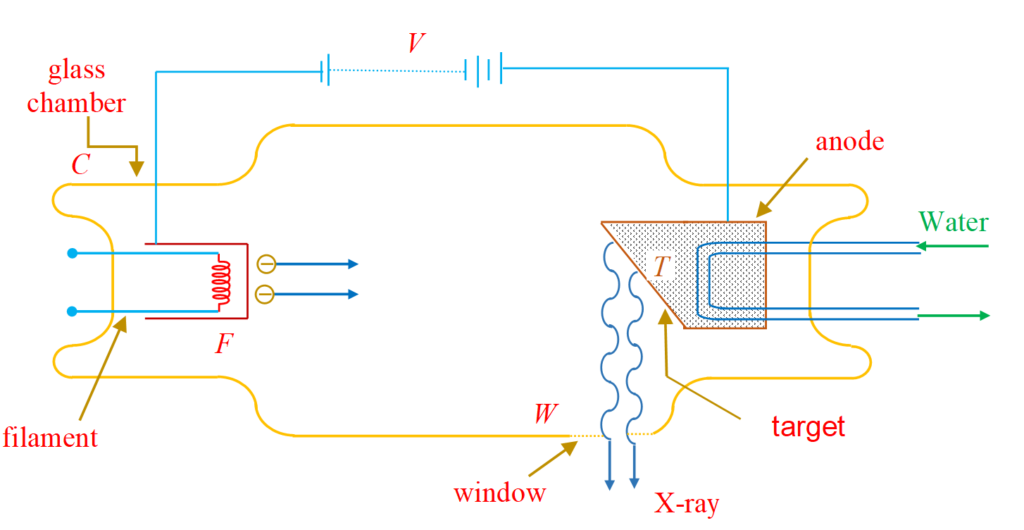
A filament F and a metallic target T are fixed in an evacuated glass chamber C. The filament is heated electrically and emits electrons by thermionic emission. A constant potential difference of several kilovolt is maintained between the filament and the target using a dc power supply so that the target is at a higher potential than the filament. The electrons emitted by the filament are, therefore, accelerated by the electric field set up between the filament and the target and hit the target with a very high speed. These electrons are stopped by the target and in the process X-rays are emitted. These X-rays are brought out of the tube through a window W made of thin mica or mylar or some such material which does not absorb X-rays appreciably. In this process, large amount of heat is developed, and thus an arrangement is provided to cool down the tube continuously by running water.

Continuous And Characteristic X-Rays

         When X-rays coming from a Coolidge tube are investigated for the wavelength present. We find that X-rays can be divided in two categories based on the mechanism of their generation. These X-rays are called continuous and characteristic X-rays. These X-rays have their origin in the manner in which the highly energetic electron loses its kinetic energy. As the fast moving electrons enter metal target, they starts losing their energy by collisions with the atoms of metal target. At each such collision either of the following two processes take place.

(i)

Electron loses its kinetic energy and a part of this lost kinetic energy is converted into a photon of electromagnetic radiation and the rest increases the kinetic energy of the target atoms, which ultimately heats up the target. This electromagnetic radiation is nothing but continuous X-rays. The fraction of kinetic energy converting into energy of photon varies from one collision to the other and the energy of such photon will be maximum when electron converts all its energy into a photon in the first collision itself.

         If electron are accelerated through a potential difference V, then maximum energy of emitted photon could be  Emax⁡ \displaystyle {{E}_{{\max }}} = eV , hcλmin⁡ \frac{{hc}}{{{{\lambda }_{{\min }}}}} = eV , λmin⁡ \displaystyle {{\lambda }_{{\min }}} = hceV \frac{{hc}}{{eV}}            

         λmin⁡ \displaystyle {{\lambda }_{{\min }}} is also called cut off wavelength. Since electron may loose very small energy in a given collision, the upper value of λ\lambda will approach to infinity. However both the cases e.g. electron converting all its energy in one will go and loosing very small energy will have very small probability. That explains the origin of continuous X-ray. We can also see from the discussion, which we have had on continuous X-rays that λmin⁡ \displaystyle {{\lambda }_{{\min }}} depends only on accelerating voltage applied on the electron and not on the material of the target.

(ii)

The electron A knocks out an inner  shell electron C of the atom with which it collides. Let us take a hypothetical case of a target atom whose K-shell electron has been knocked out as shown.

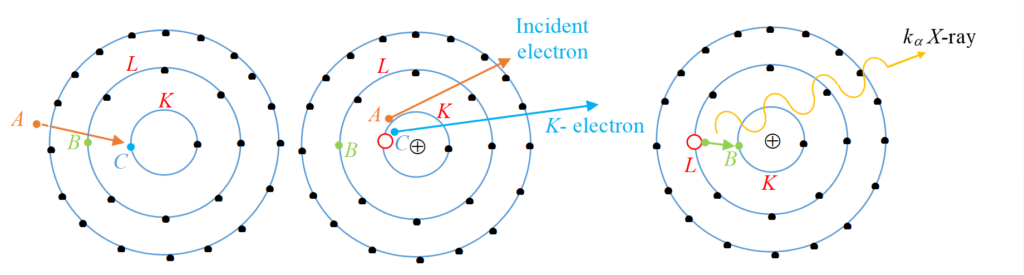
This will create a vacancy in K-shell shown by red circle. Sensing this vacancy an electron B from a higher energy state say L shell may make a transition to this vacant state. When such a transition takes place the difference of energy is converted into photon of electromagnetic radiation, which is called characteristic X-rays. Now depending upon which shell electron makes a transition to K-shell we may have different K X-rays e.g. if electron from L shell jumps to K shell we have Kα \displaystyle {{K}_{\alpha }}, if electron from M shell jumps to K shell, we have Kβ \displaystyle {{K}_{\beta }} X-ray and so on. Similarly if vacancy has been caused in L shell we may have Lα \displaystyle {{L}_{\alpha }}, Lβ \displaystyle {{L}_{\beta }}  X-ray etc depending on whether we have transition of electron from M shell or N shell. 

Below we have shown the production of characteristic x rays i.e. Kα,Kβ,… {{K}_{\alpha}},{{K}_{\beta}},… and Lα,Lβ,… {{L}_{\alpha}},{{L}_{\beta}},… on a energy level diagram.

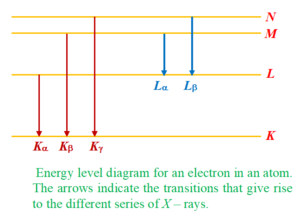
Since emission of characteristic X-ray involves the inner material energy levels of target atom, therefore the wavelength of characteristic X-ray depends on the target. If we plot curve between intensity of different wavelength components of X-ray coming out of a Coolidge tube and wavelength, it is like a figure given below:

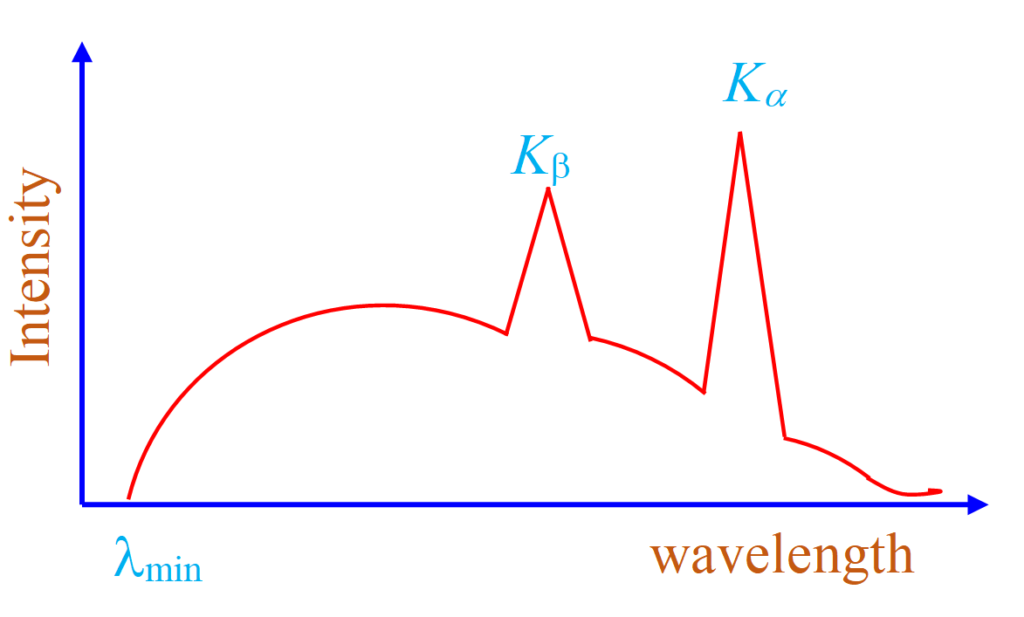
As we can see from the curve, at certain clearly defined wavelengths, the intensity of X-rays is very large. These X-rays are known as characteristic X-rays. It is also clear from the curve that λkβ {{\lambda }_{{{{k}_{\beta }}}}}is greater than λkα {{\lambda }_{{{{k}_{\alpha }}}}}however intensity of Ka transition is more as compared to the intensity of Kβ \displaystyle {{K}_{\beta }}  transition

It is primarily because transition probability of Kα \displaystyle {{K}_{\alpha}}  is more as compared to transition probability of Kβ \displaystyle {{K}_{\beta }}. At other wavelengths intensity varies gradually and these are called continuous X-rays.

Moseley’s law

         Moseley conducted many experiments on characteristic X-rays, the findings of which played an important role in developing the concept of atomic number. Moseley’s observations can be expressed as f =a(Zb) \displaystyle \sqrt{f}~=a\left( {Zb} \right) ,where a and b are constants, Z is the atomic number of target atom and f is the frequency of characteristic X-rays.

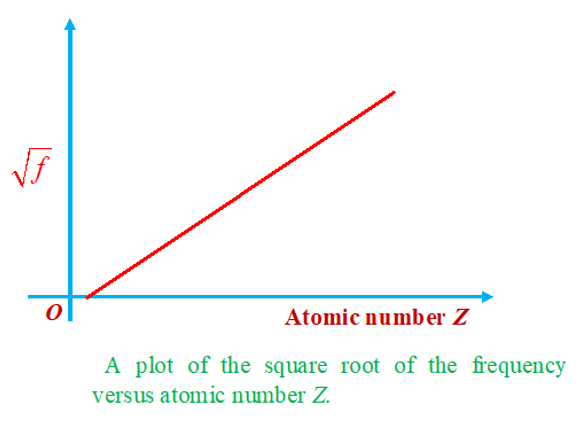
Moseley’s law can be easily understood on the basis of Bohr’s atomic model. Let us consider an atom from which an electron from K-shell has been knocked out, an L shell electron which is about to make transition to the vacant site will find the charge of nucleus is screened by the spherical cloud of remaining one electron in the K shell. If the effect of outer electrons and other L-electrons are neglected then electron making the transition will find a charge (Z – 1)e at the centre. Hence we may expect Bohr’s model to give expected result if we replace Z by (Z – 1).

According to Bohr’s model, the energy released during a transition from n = 2 to n = 1 is given by

ΔE=Rhc(Z1)2 \displaystyle \Delta E=Rhc{{\left( {Z1} \right)}^{2}} (112 − 122) \left( {\frac{1}{{{{1}^{2}}}}\,-\,\frac{1}{{{{2}^{2}}}}} \right)         

hf = Rhc (34) \left( {\frac{3}{4}} \right) (Z1)2 \displaystyle {{\left( {Z1} \right)}^{2}}

f = 3Rc4 \sqrt{{\frac{{3Rc}}{4}}} (Z – 1)

Which is same as Moseley’s equation with b = 1 & a = 3Rc4 \sqrt{{\frac{{3Rc}}{4}}}.

Properties of X-rays

(i)  X-rays being an electromagnetic wave travel with a speed equal to the speed of light. 

(ii) X-rays are not responsive to electric or magnetic field. 

(iii) X-rays when pass through gases, produce ionisation.

(iv) X-rays can effect photographic plates and exhibit the phenomenon of fluorescence.

Illustration

Find the cut-off wavelength of the X-rays emitted by an X-ray tube operating at 30 kV.

Solution

For minimum wavelength, the total kinetic energy should be converted into an X-ray photon.

Thus,

λmin⁡ \displaystyle {{\lambda }_{{\min }}}=  hcE=12400E=1240030×103\frac{{hc}}{E}=\frac{{12400}}{E}=\frac{{12400}}{{30\times {{{10}}^{3}}}} = 0.41 Å

Illustration

Show that the frequency of Kβ \displaystyle {{K}_{\beta }} X-ray of a material equals to the sum of frequencies of Kα \displaystyle {{K}_{\alpha }} and Lα \displaystyle {{L}_{\alpha }}  X-rays of the same material.

Solution

The energy level diagram of an atom with one electron knocked out is shown above.

Energy of Kα \displaystyle {{K}_{\alpha }} X-ray is

EKα=EL−EK \displaystyle {{E}_{{K\alpha }}}={{E}_{L}}-{{E}_{K}}

Energy of Kβ \displaystyle {{K}_{\beta }} X-ray is

EKβ=EM−EK {{E}_{{{{K}_{\beta }}}}}={{E}_{M}}-{{E}_{K}}

 and,    Energy of Lα \displaystyle {{L}_{\alpha }} X-ray is

ELα=EM−EL {{E}_{{{{L}_{\alpha}}}}}={{E}_{M}}-{{E}_{L}}

thus,    EKβ=EKα+ELα {{E}_{{{{K}_{\beta }}}}}={{E}_{K\alpha}}+{{E}_{L\alpha}}

or        fKβ=fKα+fLα {{f}_{{{{K}_{\beta }}}}}={{f}_{{{{K}_{\alpha }}}}}+{{f}_{{{{L}_{\alpha }}}}}

Illustration

If the shortest wavelengths of the continuous spectrum coming out of a Coolidge tube is 0.1Ao \displaystyle {{A}^{o}}. Find the de Broglie wavelength of the electron reaching the target metal in the Coolidge tube (approximately) (given hc = 12400 eVAo \displaystyle {{A}^{o}}, h = 6.63×1034 \displaystyle 6.63\times {{10}^{{34}}} in MKS, mass of electron = 9.1×1031 \displaystyle 9.1\times {{10}^{{31}}} kg) 

Solution

Kinetic energy of the electron reaching the target metal = maximum kinetic energy of x-ray photon =  124000.1eV \frac{{12400}}{{0.1}}eV = 124000 eV = 124 x 1.6 x 10–16 J

de Broglie wavelength of the electron

λ=h2mK \lambda=\frac{h}{{\sqrt{{2mK}}}}

hence λ=6.63×10−342×9.1×10−31×124×1.6×10−16 \lambda=\frac{{6.63\times {{{10}}^{{-34}}}}}{{\sqrt{{2\times 9.1\times {{{10}}^{{-31}}}\times 124\times 1.6\times {{{10}}^{{-16}}}}}}}

therefore λ=0.035Ao \lambda= 0.035 \displaystyle {{A}^{o}}

Illustration

When the voltage applied to an X-ray tube is increased from 10 kV to 20 kV the wavelength interval between the Kα \displaystyle {{K}_{\alpha }} line and the short wave cut off of the continuous X-ray spectrum increases by a factor 3. Find the atomic number of element of which the tube anti-cathode is made. (Rydberg’s constant = 107 \displaystyle {{10}^{{7}}} m–1)                                     

Solution

λC1 {{\lambda }_{{{{C}_{1}}}}}= hceV = 1237510 × 103 A∘ \frac{{hc}}{{eV}}\,=\,\frac{{12375}}{{10\,\times \,{{{10}}^{3}}}}\,A{}^\circ = 1.2375 Ao \displaystyle {{A}^{o}}                                                     … (1)

similarly λC2 =  {{\lambda }_{{{{C}_{2}}}}}\,=\,0.61875 Ao \displaystyle {{A}^{o}}         … (2)

1λKα \frac{1}{{{{\lambda }_{{{{K}_{\alpha }}}}}}}= (Z−1)2 \displaystyle {{\left( {Z-1} \right)}^{2}} {11−14} × 107 \left\{ {\frac{1}{1}-\frac{1}{4}} \right\}\,\times \,{{10}^{7}}         … (3)

It is given

 3 × (λKα \displaystyle {{\lambda }_{{K\alpha }}} – 1.2375) = λKα \displaystyle {{\lambda }_{{K\alpha }}} – 0.61875

hence  λKα \displaystyle {{\lambda }_{{K\alpha }}}= 1.54338 Ao \displaystyle {{A}^{o}}        … (4)

Putting this value in (3)

Z –1 = 29

hence Z = 30

Illustration

A X-ray tube is operating at 12 kV and 5 mA. Calculate the number of electrons striking the target per second and the speed of striking electrons.

Solution

We know that             I=Qt=net \displaystyle I=\frac{Q}{t}=\frac{{ne}}{t}

Where, n is number of electrons striking the target per second

hence n=I.te=5×10−3×11.6×10−19 \displaystyle n=\frac{{I.t}}{e}=\frac{{5\times {{{10}}^{{-3}}}\times 1}}{{1.6\times {{{10}}^{{-19}}}}}

therefore n=3.125×1016/sn=3.125\times {{10}^{{16}}}/s

Also   v=2eVm \displaystyle v=\sqrt{{\frac{{2eV}}{m}}}

=(2×1.6×10−19×12×103/9.1×10−31)1/2 \displaystyle ={{\left( {2\times 1.6\times {{{10}}^{{-19}}}\times 12\times {{{10}}^{3}}/9.1\times {{{10}}^{{-31}}}} \right)}^{{1/2}}}

=6.49×107m/s \displaystyle =6.49\times {{10}^{7}}m/s

Illustration

In certain element the K electron energy is -18.525 ke V and the L electron energy is – 3 keV. When an electron jumps from the L to K shell, an X-ray photon is emitted. Calculate the wavelength of the X-rays.

Solution

Using Moseley’s law, we get

f1f2=b(Z1−a)b(Z2−a) \displaystyle \frac{{\sqrt{{{{f}_{1}}}}}}{{\sqrt{{{{f}_{2}}}}}}=\frac{{b\left( {{{Z}_{1}}-a} \right)}}{{b\left( {{{Z}_{2}}-a} \right)}}

or  c/λ1c/λ2=(Z1−a)2(Z2−a)2 \displaystyle \frac{{c/{{\lambda }_{1}}}}{{c/{{\lambda }_{2}}}}=\frac{{{{{\left( {{{Z}_{1}}-a} \right)}}^{2}}}}{{{{{\left( {{{Z}_{2}}-a} \right)}}^{2}}}}

or  λ2=λ1(Z1−a)2/(Z2−a)2 \displaystyle {{\lambda }_{2}}={{\lambda }_{1}}{{\left( {{{Z}_{1}}-a} \right)}^{2}}/{{\left( {{{Z}_{2}}-a} \right)}^{2}}

hence    λ2=200×(74−1)2/(78−1)2 \displaystyle {{\lambda }_{2}} =200\times {{\left( {74-1} \right)}^{2}}/{{\left( {78-1} \right)}^{2}}

or  λ2=179.76A˚ \displaystyle {{\lambda }_{2}}=179.76{\AA}

Practice Questions (Basic Level)

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

Practice Questions (JEE Main Level)

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

Practice Questions (JEE Advance Level)

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.