Video Lecture
Theory For Making Notes
Different ways of electron emission
The free electrons can be emitted from the surface of the metal when a sufficient amount of energy is supplied to them. This energy can be supplied in different ways hence there are different types of emission process which are given below
(a) Thermionic emission
It is the phenomenon of emission of electrons from the metal surface when heated suitably. Here the energy required for the emission of electrons from metal surface is supplied by thermal energy. The emitted electrons are called thermal electrons or thermions.
(b) Photoelectric emission
It is the phenomenon of emission of electrons from the surface of metal when light radiations of suitable frequency fall on it. Here the energy to the free electrons for their emission is supplied by photon of light. The emitted electrons are called photoelectrons.
(c) Field emission or cold cathode emission
It is the phenomenon of emission of electrons from the surface of a metal under the application of a strong electric field. When a very strong electric field ( \displaystyle \sim{{10}^{8}}V{{m}^{{1}}}) is applied to metal, it emits electrons.The field emission can be obtained at temperatures much lower than required for Thermionic emission and therefore, sometimes it is called cold cathode emission or auto electronic emission.
(d) Secondary emission
It is the phenomenon of emission of electrons from the surface of metal in large number when fast moving electron (called primary electrons) strike the metal surface. The fast moving electrons are high–energy electrons. As they fall on the metal surface, they transfer their energy to the free electrons of the metal by which their energy becomes more than the \displaystyle {{W}_{o}}rk function of the metal and they are emitted from the metal surface.
Photon
Light travels in the form of packets of energy or in the form of quanta of energy. This is called photon. Energy of a photon is given by Planck as E=h\nu, where h is the Planck’s constant.
The photon has following properties
(a) Photon travels in a straight line.
(b) The photons emitted from a source, travel through space with the same speed, which is equal to the speed of light.
(c) The frequency of a photon does not change when it travels through different media as the velocity of a photon is different in different media.
(d) The rest mass of a photon is zero.
(e) According to Einstein’s mass energy relationship, a photon of frequency ‘ \displaystyle v ’ has its equivalent mass given by
\displaystyle hv=m{{c}^{2}} or m=\frac{{hv}}{{{{c}^{2}}}}
The mass m is called dynamic mass.
So we can say that the dynamic mass of \displaystyle \gamma -ray photons is more than the mass of X-ray photon.
(g) The momentum of photon is p=\frac{E}{c}=\frac{{hv}}{c}=\frac{h}{\lambda }.
Photoelectric Effect
The emission of electrons from a metallic surface when irradiated by electromagnetic radiation is called the phenomenon of photoelectric effect. The emitted electrons are called as photoelectrons.
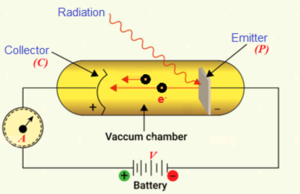
For the investigation of the photoelectric effect a schematic diagram of the apparatus as used by Lenard (1902) is shown in the figure. Monochromatic light from the source illuminates a plate P (Metal Surface) in an evacuated glass enclosure (Vacuum Chamber). As a result electrons are ejected from the metal surface. These ejected electrons are called photoelectrons. A battery `V’ maintains a potential difference between metal `P’ and a detector (metal cylinder C), which collects the photoelectrons. The potential of C can be varied to be either positive or negative polarity relative to P. When the collector is positive with respect to the plate, the electrons are attracted to it and the ammeter (A) registers a current.
The result of observations are also called the laws of photoelectric emission which are as follows:
Laws of photoelectric emission
(a) The number of photoelectrons emitted is independent of the frequency of incident light and is directly proportional to the intensity of the incident light.
(b) For a given metal, there exists a certain minimum frequency of the incident radiation below which no emission of photoelectrons takes place. This frequency is called threshold frequency.
(c) The maximum kinetic energy with which an electron is emitted from a metal surface is independent of the intensity of incident light and depends upon its frequency.
(d) The photoelectric emission starts as soon as the light is incident on the metal surface hence it is instantaneous.
Some important terms
Work function or Threshold energy ( \displaystyle {{W}_{o}} or {{\phi}_{o}})
The minimum energy of incident radiation, required to eject the electrons from metallic surface is defined as work function of that surface.
{{W}_{0}}=h{{\nu }_{0}}=\frac{{hc}}{{{{\lambda }_{0}}}}; in this equation \displaystyle {{\nu }_{0}} is threshold frequency, \displaystyle {{\lambda }_{0}} is threshold wavelength and all the quantities are in S.I. units.
Usually work function is given in electron volts, so we multiply the LHS of the above equation by `e’ that is the charge of an electron to get the units in Joules
Hence we get {{W}_{o}}=\frac{{hc}}{{e{{\lambda }_{0}}}}. here \frac{{hc}}{e} is a constant which is equal to \displaystyle 12375\times {{10}^{{-10}}}.
therefore {{W}_{o}}=\frac{{12375}}{{{{\lambda }_{0}}}}\times {{10}^{{-10}}} here wavelength is in meter
or {{W}_{o}}=\frac{{12375}}{{{{\lambda }_{0}}}}ev here wavelength is in \displaystyle {{A}^{o}} and the work function in eV
Threshold frequency ( \displaystyle {{\nu }_{0}})
The minimum frequency of incident radiations required to eject the electron from metal surface is defined as threshold frequency.
{{W}_{0}}=h{{\nu }_{0}}\text{ } Here \displaystyle {{\nu }_{0}} is threshold frequency in Hz and {{W}_{0}} is in Joules
If incident frequency is less than the threshold frequency then no photoelectron emission takes place.
The threshold frequency is a characteristic of the metal plate.
Threshold wavelength ( \displaystyle {{\lambda }_{0}})
The maximum wavelength of incident radiations required to eject the electrons from a metallic surface is defined as threshold wavelength.
{{W}_{0}}=\frac{{hc}}{{{{\lambda }_{0}}}}; Here \displaystyle {{\lambda }_{0}} is threshold wavelength in meter and {{W}_{0}} is in Joules
If incident wavelength is more than the threshold wavelength then no photoelectron emission takes place
FACTORS AFFECTING THE PHOTOELECTRIC CURRENT
In the experiment with the above setup Lenard studied the dependence of photoelectric current on the following factors.
(i) Intensity of incident radiation
(ii) Potential difference between the plate and the collector
(iii) Frequency of the incident radiation
Effect of the intensity of Incident Radiation
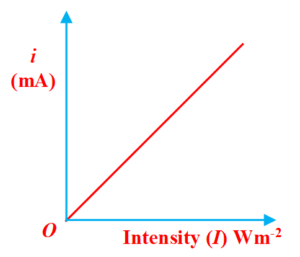
When the collector is positive relative to the plate and the potential difference is kept fixed, then for a given frequency of radiation, the photoelectric current is proportional to the intensity of the light, as shown in figure. It shows that the number of emitted photoelectrons is proportional to the light intensity. Furthermore, there is no threshold intensity.
Effect of Potential Difference
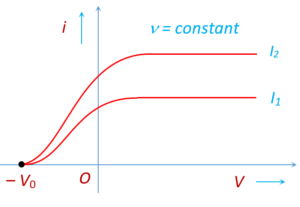
When the frequency and intensity of radiation are kept constant and the positive potential of collector relative to plate is gradually increased, then the photoelectric current i increases with the potential difference V. At some value of the potential difference, when all the emitted electrons are collected, thus increasing potential difference has no effect on the current. The current has reached its maximum value, called the saturation current.
When the polarity of the battery is reversed, the electrons are repelled and only the most energetic ones reach the collector, so the current falls. When the retarding potential difference reaches a critical value, the current drops to zero. At this stopping potential \displaystyle {{V}_{0}}, only those electrons with the maximum kinetic energy are able to reach the collector.
\displaystyle {{V}_{0}}.e= \frac{1}{2}mv_{{\max }}^{2}
For a given frequency of light, the saturation current depends on the intensity of light. Larger the intensity; higher the saturation current. However, the stopping potential does not change with the intensity. It is clearly shown in figure given below
Effect of frequency
For a given intensity of radiation, the stopping potential depends on the frequency. Higher the frequency, higher the value of stopping potential.
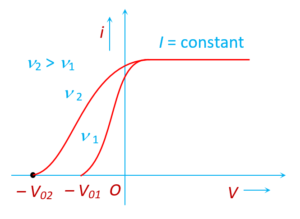
The maximum kinetic energy of the electrons depends on the light source and the plate material, but not on the intensity of the source. Certain combinations of light sources and plate materials exhibit no photoelectric effect.
Einstein’s Theory of Photoelectric Effect
According to Einstein, the experimental results of photoelectric effect can be explained by applying the quantum theory of light. He assumed that light of frequency \displaystyle \nu contain packets or quanta of energy
\displaystyle E=h\nu . On this basis, light consists of particles, and these are called photons. The number of photons per unit area of cross-section of the beam of light per second is proportional to its intensity. But the energy of photon is proportional to its frequency and is independent of the light intensity.
In the process of photo emission a single photon gives up all its energy to a single electron. As a result, the electron is ejected instantaneously. Since the intensity of light is determined by the number of photons incident, therefore, increasing the intensity will increase the number of ejected electrons.
The maximum possible kinetic energy \left( {\frac{1}{2}mv_{{max}}^{2}} \right) of the photoelectrons is determined by the energy of each photon ( \displaystyle \nu ) according to the Einstein equation
\frac{1}{2}mv_{{\max }}^{2}=h\nu -{{W}_{o}}
where the work function, ( \displaystyle {{W}_{o}}), is the minimum energy needed to extract an electron from the surface of the material.
In terms of threshold frequency, it is given by \displaystyle {{W}_{o}} = \displaystyle {{\nu}_{o}}
Using the above equation , we may write equation as
\displaystyle \frac{1}{2}mv_{{max}}^{2}=h\nu -h{{\nu }_{o}}
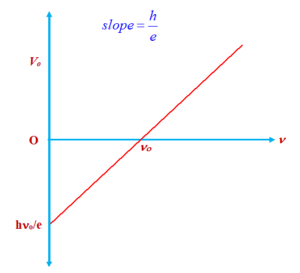
hence \displaystyle \frac{1}{2}mv_{{max}}^{2}=h(\nu -{{\nu }_{o}}) —–(A)
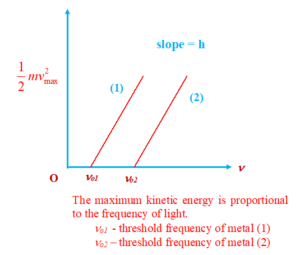
In equation (A) if we put \frac{1}{2}mv_{{\max }}^{2}={{V}_{o}}e then
we get {{V}_{o}}e=h\nu -h{{\nu }_{o}}
or {{V}_{o}}=\frac{h}{e}\nu -\frac{h}{e}{{\nu }_{o}}
The graph between \displaystyle {{V}_{o}} and \displaystyle \nu is a straight line with a slope equal to \frac{h}{e}.
Calculation for photoelectric current
Consider a case where a metal surface of area `A’ is kept at a distance `r’ from a source of radiation.
Let P be the power of the point source of radiations, then intensity I at
a distance r from the source can be calculated by considering a spherical surface around it of radius r.
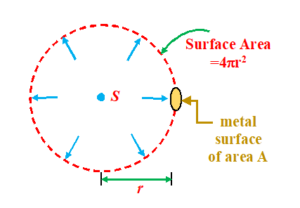
This means that the energy falling on the whole surface area (i.e. \displaystyle 4\pi {{r}^{2}}) of sphere due to source is P joules/sec. Hence say in `t’ seconds the energy falling on the spherical surface is E=Pxt
If I be the intensity of light on the surface. We know that the intensity is the amount of energy falling per unit area per sec so
I=\frac{E}{{surface\text{ }area}}=\frac{{P\times t}}{{4\pi {{r}^{2}}}} (here put t=1 sec)
Hence I = \frac{P}{{4\pi {{r}^{2}}}} ( \displaystyle W/{{m}^{2}})
Now if A is the small area of a metal plate on which radiations are incident, then the power received by this metal surface is
\displaystyle {{{P}^{\prime}}} = IA = \left( {\frac{P}{{4\pi {{r}^{2}}}}} \right)A (W)
If \displaystyle v is the frequency of radiation, then the energy of photon is given by
\displaystyle E=h\nu
The number of photons incident on the plate per second (called photon flux) is given by
\displaystyle \Phi =\frac{{{{{P}}^{\prime}}}}{E}=\left[ {\frac{{\frac{P}{{4\pi {{r}^{2}}}}\times A}}{{h\nu }}} \right]
If \displaystyle v>{{\nu }_{0}} (threshold frequency) and photon efficiency of the metal plate is \displaystyle \eta \%, then the number of photoelectrons emitted per second is given by
n = \frac{{\Phi \eta }}{{100}}=\left[ {\frac{{\frac{P}{{4\pi {{r}^{2}}}}\times A}}{{h\nu }}} \right]\frac{\eta }{{100}}
Finally, the photocurrent i is given by
i = ne
Where e is the charge of an electron
Note :
If the area of the metal plate is large and it is kept near a source then it is better to use the concept of solid angle to find the amount of radiations or Energy falling on it.
Photoelectric Cell or photocell
The photo cell is based on the fact that electrons are emitted from a photosensitive surface by the action of light. Photoelectric current is very small.
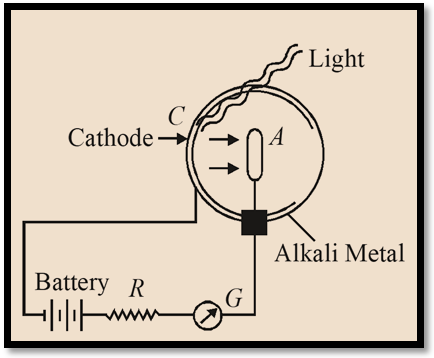
To increase current inert gases like Argon is filled at low pressure. The cell is now called gas–filled photo emissive cell.
The photo–electrons emitted by cathode ionize the gas by collision and hence the current is increased. This is used as a switch. Its is also used in photometry, Television, Cinematography, recording and reproduction of sound.
Applications of photoelectric cells
The photoelectric cell are used in
(a) the reproduction of sound in motion pictures.
(b) automatic switches for street lights.
(c) scanning system.
(d) automatic door system
(e) controlling temperature in furnace and chemical reactions.
(f) automatic counting of parts manufactured by a machine or number of persons crossing a point or entering a room.
Illustration
Ultraviolet light of wavelength 2000 \displaystyle {{A}^{o}} causes photoemission from a surface. The stopping potential is 2V.
(a) Find the work function in eV
(b) Find the maximum speed of the photoelectrons.
Solution
(a) Using Einstein relation
W = \frac{{hc}}{\lambda }-e{{V}_{o}}
or W = \frac{{12400}}{{2000}}-2=4.2eV
(b) Since \frac{1}{2}mv_{{\max }}^{2}=e{{V}_{o}}
hence \displaystyle {{v}_{{max}}} = \sqrt{{\frac{{2e{{V}_{o}}}}{m}}}
=\sqrt{{\frac{{2\left( {1.6\times {{{10}}^{{-19}}}} \right)\left( 2 \right)}}{{9.1\times {{{10}}^{{-31}}}}}}}
or \displaystyle {{v}_{{max}}}=8.4\times {{10}^{5}} m/s
Illustration
The intensity of sunlight on the surface of earth is 1400 \displaystyle W/{{m}^{2}}. Assuming the mean wavelength of sunlight to be 6000 \displaystyle {{A}^{o}}, calculate
(a) the photon flux arriving at 1 \displaystyle {{m}^{2}} area on earth perpendicular to light radiations, and
(b) the number of photons emitted from the sun per second assuming the average radius of Earth’s orbit is \displaystyle 1.49\times {{10}^{{11}}}m.
Solution
(a) Energy of a photon E = \frac{{hc}}{\lambda }
=\frac{{12400}}{{6000}}=2.06\,eV=3.3\times {{0}^{{-19}}}\,J
we know that photon flux = \frac{{IA}}{E}
hence Photon flux = \frac{{\left( {1400} \right)\left( 1 \right)}}{{3.3\times {{{10}}^{{-19}}}}}
so Photon flux = \displaystyle 4.22\times {{10}^{{21}}}
(b) n = \frac{P}{E}=\frac{{I\left( {4\pi {{R}^{2}}} \right)}}{E}
or n = \frac{{\left( {1400} \right)\left( {4\pi } \right){{{\left( {1.49\times {{{10}}^{{11}}}} \right)}}^{2}}}}{{3.3\times {{{10}}^{{-19}}}}}
hence n = \displaystyle 1.18\times {{10}^{{45}}}
Illustration
The emitter in a photoelectric tube has a threshold wavelength of 6000 \displaystyle {{A}^{o}}. Determine the wavelength of the light incident on the tube if the stopping potential for this light is 2.5V.
Solution
The work function is
{{W}_{0}}=h{{\nu }_{{th}}}=\frac{{hc}}{{{{\lambda }_{{th}}}}},
hence {{W}_{0}}=\frac{{12.4\times {{{10}}^{3}}\ \text{eV}.{\AA}}}{{6000{\AA}}}=2.07\ \text{eV}
The photoelectric equation then gives
e{{V}_{s}}=h\nu -{{W}_{0}}=\frac{{hc}}{\lambda }-{{W}_{0}}
or
2.5=\frac{{12.4\times {{{10}}^{3}}}}{\lambda }-2.07
Solving, \displaystyle \lambda = 2713 \displaystyle {{A}^{o}}.
Illustration
Prove that the photoelectric effect cannot occur for free electrons. Or Prove that a single free electron can’t absorb a photon completely.
Solution
Look at the hypothetical process in the centre-of-mass shown in figure, which is defined as that system in which the initial momentum is zero. From conservation of energy,
\displaystyle {{E}_{{initial}}}={{E}_{{final}}}~
or \displaystyle h\nu +m{{c}^{2}}={{m}_{0}}{{c}^{2}}
which implies \displaystyle {{m}_{0}}>m. Since this cannot be true, the process cannot occur.
The electrons participating in the photoelectric effect are not free. The heavy matter present takes off momentum but absorbs a negligible amount of energy.

Illustration
When photons of energy 5 eV strike the surface of a metal A, the ejected photoelectrons have maximum kinetic energy \displaystyle {{K}_{A}} eV and de Broglie wavelength \displaystyle {{\lambda}_{A}}. The maximum kinetic energy of photoelectrons liberated from another metal B by photons of energy 5.30 eV is \displaystyle {{K}_{B}}=\left( {{{K}_{A}}-\text{ }1.5} \right). eV. If the de Broglie wavelength of these photoelectrons is \displaystyle {{\lambda }_{B}}=\text{ }2{{\lambda }_{A}}, then find \displaystyle {{K}_{A}} and \displaystyle {{K}_{B}}.
Solution
\displaystyle {{K}_{A}} = \frac{{hc}}{\lambda }\,-\,{{W}_{A}}=5-{{W}_{A}} … (1)
\displaystyle {{K}_{B}} = 5.3 – \displaystyle {{W}_{B}} … (2)
It is given \displaystyle {{K}_{B}} = \displaystyle {{K}_{A}} – 1.5 … (3)
\displaystyle \lambda = \frac{h}{P}\,=\,\frac{h}{{\sqrt{{2mK}}}}
from given data we have \lambda _{B}^{2} = 4 \lambda _{A}^{2}
\frac{{{{h}^{2}}}}{{2{{m}_{e}}{{K}_{B}}}}\,=\,\frac{{4{{h}^{2}}}}{{2{{m}_{e}}{{K}_{A}}}}
hence \displaystyle {{K}_{A}}=\text{ }4{{K}_{B}} … (4)
Since \displaystyle {{K}_{B}}=\text{ }4{{K}_{B}}-\text{ }1.5
so \displaystyle 3{{K}_{B}}=\text{ }1.5
hence \displaystyle {{K}_{B}} = 0.5 eV
and \displaystyle {{K}_{A}} = 2eV
Illustration
The work function \displaystyle {{W}_{A}} for photoelectric material A is 2 eV and \displaystyle {{W}_{B}} for another photoelectric material B is 4 eV. If photons of energy \displaystyle {{E}_{A}} strike the surface of A, the ejected photoelectrons have a minimum de Broglie wavelength and photons of energy \displaystyle {{E}_{B}} strike the surface B, the ejected photoelectrons also have a minimum de Broglie wavelength. If \displaystyle {{E}_{B}}-{{E}_{A}}=0.5eV and \displaystyle {{V}_{A}} and \displaystyle {{V}_{B}} are the respective stopping potentials, find \displaystyle {{V}_{A}}-{{V}_{B}}. Solution
For the material A,
\displaystyle {{E}_{A}}-{{W}_{A}}=h{{\nu }_{A}} … (i)
For the material B,
\displaystyle {{E}_{B}}-{{W}_{B}}=h{{\nu }_{B}} … (ii)
Subtracting (ii) from (i), we have
\displaystyle h({{\nu }_{A}}-{{\nu }_{B}})= (1.5 × e) J … (iii)
Now, \displaystyle e{{V}_{A}}=h{{\nu }_{A}}
and \displaystyle e{{V}_{B}}=h{{\nu }_{B}}
therefore \displaystyle e({{V}_{A}}-{{V}_{B}})=h({{\nu }_{A}}-{{\nu }_{B}})
or, \displaystyle e({{V}_{A}}-{{V}_{B}})= 1.5 × e
hence \displaystyle {{V}_{A}}-{{V}_{B}}= 1.5 V
Illustration
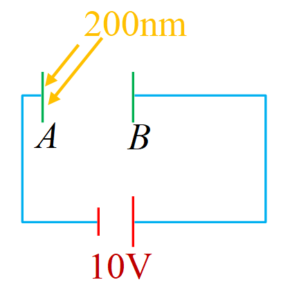
In the figure shown electro magnetic radiations of wave length 200nm are incident on a metallic plate A. The photoelectrons are accelerated by a potential difference 10V. These electrons strike another metal plate B from which electro magnetic radiations are emitted. The minimum wavelength of emitted photons is 100nm. If the \displaystyle {{W}_{o}}rk function of the metal A is found to be ( \displaystyle x\times {{10}^{{1}}}) eV, then find the value of x (given hc = 1240 eV- nm)
Solution
Incident energy of photons = \frac{{hc}}{{200}}=6.2eV
6.2={{K}_{1}}+{{W}_{0}},
{{K}_{1}}=6.2-{{W}_{0}},
{{K}_{2}}={{K}_{1}}+e\times10=16.2-{{W}_{0}}
{{K}_{2}}={{\frac{{hc}}{\lambda }}_{{\min }}}=12.4
on solving we get {{W}_{0}}=3.8eV
hence x = 38
Practice Questions (Basic Level)
1.
If a surface has a work function 4.0 eV, what is the maximum velocity of electrons liberated from the surface when it is irradiated with ultra violet radiation of wavelength 0.2 µm?
(a)4.4 × 105 m/s
(b)8.8 × 107 m/s
(c)8.8 × 105 m/s
(d)4.4 × 107 m/s.
Ans (c)
2.
The work function for Aluminium surface is 4.2 eV. The cut off wavelength for the photoelectric effect for the surface is
(a)1500 Å
(b)2955 Å
(c)3100 Å
(d)4200 Å.
Ans (b)
3.
If the frequency of light in a photoelectric experiment is doubled the stopping potential will be
(a) halved
(b) doubled
(c) more than double
(d) less than double
Ans (c)
4.
If the distance of 100 watt lamp is increased from the photo cell, the saturation current i in the photocell varies with the distance d as
(a) \displaystyle i\propto {{d}^{2}}
(b) \displaystyle i\propto d
(c) i\propto \frac{1}{d}
(d) i\propto \frac{1}{{{{d}^{2}}}}.
Ans (d)
5.
Light of wavelength 3500 Å is incident on two metals A and B whose work functions are 4.2 eV and 1.9 eV respectively. Photoelectrons will be emitted by
(a) metal A only
(b) metal B only
(c) both A and B
(d) none
Ans (b)
6.
If the speed of photoelectrons is 104 ms–1, what should be the frequency of incident radiation on the potassium metal? Work function of potassium = 2.3 eV.
(a) 8.5 × 1018 Hz
(b) 6.9 × 1018 Hz
(c) 5.5 × 1018 Hz
(d) 2.0 × 1018 Hz
Ans (b)
6.
The work function for a metal surface is 2.0 eV. Determine the longest wavelength that will eject photoelectrons from the metal surface.
(a) 6000 Å
(b) 1000 Å
(c) 4000 Å
(d) 8000 Å
Ans (a)
7.
A photosensitive metallic surface has work function hn0. If photons of energy 2hn0 falls on this surface, the electrons come out with a maximum velocity of 4 × 106 m/s. When the photon energy is increased to 5hn0, then maximum velocity of photoelectrons will be:
(a) 2 × 106 m/s
(b) 2 × 107 m/s
(c) 8 × 107 m/s
(d) 8 × 106 m/s
Ans (d)
8.
If the maximum kinetic energy of emitted photo electrons from a metal surface of work function 2.5 eV, is 1.7 eV. If wavelength of incident radiation is halved, then stopping potential will be
(a) 2.5 V
(b) 6.7 V
(c) 5 V
(d) 1.1 V
Ans (b)
9.
In a photoelectric experiment, the wavelength of incident radiation is reduced from 6000Å to 4000Å then
(a) Stopping potential will decrease
(b) Stopping potential will increase
(c) Kinetic energy of emitted electrons will decrease
(d) The value of work function will decrease
Ans (b)
10.
Figure represents the graph of kinetic energy (K) of photoelectrons (in eV) and frequency (n) for a metal used as cathode in photoelectric experiment. The work function of metal is
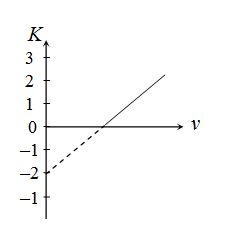
(a) 1 eV
(b) 1.5 eV
(c) 2 eV
(d) 3 eV
Ans (c)
11.
In a photoelectric effect experiment
(a) on increasing intensity and keeping frequency fixed the saturation current decreases.
(b) on increasing intensity and keeping frequency fixed the saturation current remains constant.
(c) on increasing intensity, saturation current may increase.
(d) on increasing frequency saturation current may increase.
Ans (c)
12.
When a certain metallic surface is illuminated with monochromatic light of wavelength \displaystyle \lambda , the stopping potential for photoelectric current is 3V0. When the same surface is illuminated with the light of wavelength 2 \displaystyle \lambda , the stopping potential is V0. The threshold wavelength for the surface for photoelectric effect is
(a) \frac{{4\lambda }}{3}
(b) 4 \displaystyle \lambda
(c) 6 \displaystyle \lambda
(d) 8 \displaystyle \lambda
Ans (b)
13.
The work function of aluminium is 4.2 eV. If two photons, each of energy 3.5 eV strike an electron of aluminium, then emission of electrons will be
(a) possible
(b) not possible
(c) data is incomplete
(d) depend upon the density of the surface
Ans (b)
14.
The work function for potassium is 2.25 eV. A beam with a wavelength of 400 nm has an intensity of 10-9 W/m2. Find
(a)
the maximum kinetic energy of the photoelectrons,
(a) 0.245 eV
(b) 1.045 eV
(c) 0.855 eV
(d) 10.674 eV
Ans (c)
(b)
the number of electrons emitted per meter square per second from the surface assuming 3% of the incident photons are effective in ejecting electrons.
(a) 2 x 107 m-2s-1
(b) 9 x 107 m-2s-1
(c) 13 x 107 m-2s-1
(d) 6 x 107 m-2s-1
Ans (d)
15.
The cutoff wavelength for photoemission from a material is 360 nm. What is the maximum speed of ejected electrons when it is illuminated by photons of wavelength 280 nm?
(a) 0.39 x 105 m/s
(b) 4.26 x 105 m/s
(c) 2.33 x 105 m/s
(d) 5.89 x 105 m/s
Ans (d)
16.
The threshold wavelength for cesium is 686 nm. If light of wavelength 470 nm illuminates the surface, what is the maximum speed of the photoelectrons?
(a) 5.4 x 105 m/s
(b) 10.7 x 105 m/s
(c) 4.6 x 105 m/s
(d) 3.2 x 105 m/s
Ans (a)
17.
The work function for lithium is 2.3 eV.
(a)
What is the maximum kinetic energy of photoelectrons when the surface is illuminated with light of wavelength 400 nm?
(a) 0.2 eV
(b) 0.4 eV
(c) 0.8 eV
(d) 1.5 eV
Ans (c)
(b)
If the stopping potential is 0.6 V, what is the wavelength?
(a) 428 nm
(b) 450 nm
(c) 476 nm
(d) 328 nm
Ans (a)
18.
When radiation of wavelength 350 nm is incident on a surface, the maximum kinetic energy of the photoelectrons is 1.2 eV. What is the stopping potential for a wavelength of 230 nm?
(a) 2.56 V
(b) 3.00 V
(c) 3.05 V
(d) 3.65 V
Ans (c)
Practice Questions (JEE Main Level)
1.
Radiation of two photon energies twice and five times the work function of metal are incident successively on the metal surface. The ratio of the maximum velocity of photo-electrons emitted in the two cases will be
(a)1 : 1
(b)1 : 2
(c)1 : 3
(d)1 : 4.
Ans (b)
2.
A cesium photocell with a steady potential difference of 60V across it, is illuminated by a small bright light placed 1 m away. When the same light is placed 2 m away, the electrons crossing the photocell
(a)each carry one quarter of their previous momentum
(b)each carry one quarter of their previous energy
(c)are one quarter as numerous
(d)are half as numerous.
Ans (c)
3.
The stopping potential Vs as a function of frequency of incident radiation is plotted for two different photoelectric surfaces A and B. The graphs show that the work function of A is
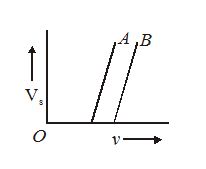
(a)greater than that of B
(b)smaller than that of B
(c)same as that of B
(d)no comparison can be done from the given graph.
Ans (b)
4.
If the wavelength of light incident on a photoelectric cell be reduced from 4000 Å to
3600 Å, then the change in the cut off potential will be
(a) 3.4 V
(b) 0.34 V
(c) 1.34 V
(d) 2.34 V
Ans (b)
5.
When a certain metallic surface is illuminated with monochromatic light of wavelength \displaystyle \lambda , the stopping potential for photoelectric current is 3V0 and when the same surface is illuminated with light of wavelength 2 \displaystyle \lambda the stopping potential is V0. The threshold wavelength of this surface for photoelectric effect is
(a)6 \displaystyle \lambda
(b) \frac{{4\lambda }}{3}
(c)4 \displaystyle \lambda
(d)8 \displaystyle \lambda .
Ans (c)
6.
Light of wavelength 0.6 mm from a sodium lamp falls on a photo cell and causes the emission of photoelectron for which the stopping potential is 0.5 volt. With light of wavelength 0.40 mm from a mercury vapour lamp the stopping potential is 1.5 volt, then value of \frac{h}{e} is
(a)4 × 10–59Vs
(b)0.25 × 1015 Vs
(c)4 × 10–15 Vs
(d)4 × 10–8 Vs.
Ans (c)
7.
The photoelectric threshold wavelength for a tungsten is 2400 Å. Determines the energy of the electrons ejected from its surface when exposed to ultraviolet radiations of wavelength 1200 Å.
(a) 1.22 eV
(b) 1.73 eV
(c) 1.30 eV
(d) 1.48 eV
Ans (d)
8.
The cathode of a photocell is irradiated with light of wavelength 3000Å. The current through the cell is found to stop when the potential of the plate is 2.1V just below the cathode. Calculate the work function of the cathode.
(a) 2.58 eV
(b) 2.00 eV
(c) 2.04 eV
(d) 1.39 eV
Ans (c)
9.
When photons of energy 4.25 eV strike the surface of a metal A, the ejected photoelectrons have maximum kinetic energy TAeV and de Broglie wavelength \displaystyle \lambda A. The maximum kinetic energy of photoelectrons liberated from another metal B by photons of energy 4.70 eV is eV. If the de Broglie wavelength of these photoelectrons is \displaystyle \lambda B = 2 \displaystyle \lambda A , then choose the incorrect statement.
(a) the work function of A is 1.25 eV
(b) the work function of B is 4.20 eV
(c) TA= 2.00 eV
(d) TB = 0.5 eV
Ans (a)
10.
In the following diagram, the relation between \displaystyle \lambda 1 and \displaystyle \lambda 2 will be
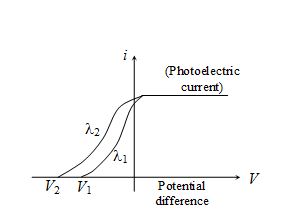
(a) {{\lambda }_{1}}=\sqrt{{{{\lambda }_{2}}}}
(b) {{\lambda }_{1}}<{{\lambda }_{2}}
(c) {{\lambda }_{1}}={{\lambda }_{2}}
(d) {{\lambda }_{1}}>{{\lambda }_{2}}
Ans (d)
11.
Two electrons of kinetic energy 2.5 eV fall on a metal plate, which has work function of
4.0 eV. Number of electrons ejected from the metal surface is
(a) one
(b) two
(c) zero
(d) more than two
Ans (c)
12.
A plate is kept in front of a beam of photons. The plate reflects 40% of the incident photons and absorbs the remainder. If the plate absorbs energy at the rate of 2000 W, find the net force acting on it.
(a) 9.33 x 10-6 N
(b) 2.83 x 10-6 N
(c) 0.33 x 10-6 N
(d) 5.22 x 10-6 N
Ans (a)
13.
A source emits monochromatic light of frequency 5.5 ´ 1014 Hz at a rate of 0.1 W. Of the photons given out, 0.15% fall on the cathode of a photocell which gives a current of 6mA in an external circuit.
(i)
Find the energy of a photon
(a) 3.8 x 10-19 J
(b) 1.9 x 10-19 J
(c) 0.3 x 10-19 J
(d) 3.6 x 10-19 J
Ans (d)
(ii)
Find the number of photons leaving the source per second.
(a) 2.8 x 1017 s-1
(b) – 2.5 x 1017 s-1
(c) 1.5 x 1017 s-1
(d) – 1.3 x 1017 s-1
Ans (a)
(iii)
Find the percentage of the photons falling on the cathode which produce photoelectrons.
(a) 1%
(b) 5%
(c) 9%
(d) 12%
Ans (c)
Practice Questions (JEE Advance Level)
1.
When a beam of 10.6 eV photons of intensity 2.0 W/m2 falls on a platinum surface of area 1.0 x 10-4 m2 and work function 5.6 eV, 0.53% of the incident photons eject photoelectrons. Find the number of photoelectrons emitted per second and their minimum and maximum energies (in eV). Take 1 eV = 1.6 x 10-19 J.
(a) 0, 5.0 eV, 3.15 x 1011
(b) 0, 5.0 eV, 8.45 x 1011
(c) 0, 5.0 eV, 6.25 x 1011
(d) 0, 5.0 eV, 0.56 x 1011
Ans (c)
