Video Lecture
Theory For Making Notes
de – BROGLIE WAVES
About two decades after the discovery of the particle properties of wave, Louis de-Broglie proposed that moving object have wave as well as particle characteristics. de-Broglie suggested that a moving particle behaves in certain ways as though it is associated with a wave.
As we know that a photon of light of frequency n has a momentum given by
p = \frac{{h\nu }}{c}\,=\,\frac{h}{\lambda }
The wavelength of a photon is therefore specified by its momentum as
\lambda \,=\,\frac{h}{p} …(i)
de-Broglie suggested that this equation is completely general one and can be applied to material particles as well as to photons.
The momentum of a particle of mass m and velocity v is p = mv,
and hence its de-Broglie wavelength is given as \lambda \,=\,\frac{h}{{mv}} …(ii)
The greater the particle’s momentum; the shorter is its wavelength.
In equation (ii), m is the relativistic mass which was given by Einstein as
m = \frac{{{{m}_{0}}}}{{\sqrt{{1-\frac{{{{v}^{2}}}}{{{{c}^{2}}}}}}}}, (here m0 is the rest mass of the particle)
The wave and particle nature of moving bodies can never be observed at the same time. In certain situations a moving body resembles a wave and in others it resembles a particle. Depending on the situation, one of the two characters dominates. Interference can only be under stood in terms of wave theory. When light of sufficiently low wavelengths falls on a metal surface, electrons are ejected. This phenomena’s is called the photoelectric effect and can be understood only in terms of the particle nature of light. The particles of light are called photons. So one cannot ask which is the correct description. All that can be said is that in certain situations a moving body resembles a wave and in others it resembles a particle.
Equivalence with Bohr’s Theory
The first step in the understanding of the hidden meaning of Bohr’s quantum orbits was made by Louis de Broglie, who tried to draw an analogy between the sets of discrete energy levels that characterize the inner state of atoms and the discrete sets of mechanical vibrations that are observed in the case of violin strings, organ pipes etc.
de Broglie asked himself,
“Could it not be that the optical properties of atoms are due to some kind of standing waves enclosed within themselves?”
As a result of these considerations, de Broglie came out with his hypothesis that the motion of electron within the atom is associated with a peculiar kind of waves which he called “pilot waves”.
In order to have n complete wavelengths ( \displaystyle n\lambda ) fit into the circumference ( \displaystyle 2\pi {{r}_{n}}~) of the nth orbit, the following relation must be true:
\displaystyle n{{\lambda }_{n}}=\text{ }2\pi {{r}_{n}}~~~~~~~~~~~~~~ —-(iii)
In other word’s the circumference of any orbit of the electron must be in integral multiple of the de-Broglie wave length (see the diagram given below)
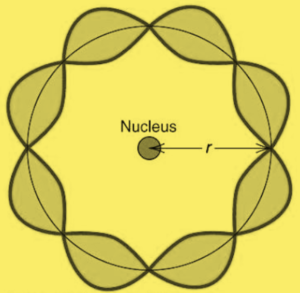
From Bohr’s theory of the hydrogen atom, the radius of the nth orbit is given by
\displaystyle {{r}_{n}} = \frac{{{{n}^{2}}{{h}^{2}}}}{{4{{\pi }^{2}}km{{e}^{2}}}}, putting it into equation (iii)
n{{\lambda }_{n}}=2\pi \left[ {\frac{{{{n}^{2}}{{h}^{2}}}}{{4{{\pi }^{2}}km{{e}^{2}}}}} \right]
or
\displaystyle n{{\lambda }_{n}} = \frac{{{{n}^{2}}{{h}^{2}}}}{{2\pi km{{e}^{2}}}}
or
\displaystyle {{\lambda }_{n}} = \frac{{n{{h}^{2}}}}{{2\pi km{{e}^{2}}}} = \frac{h}{m} \left[ {\frac{{nh}}{{2\pi k{{e}^{2}}}}} \right]
{{{\lambda }_{n}}=\frac{h}{{m{{v}_{n}}}}}
\left[ {\because \text{ }\frac{{nh}}{{2\pi k{{e}^{2}}}}=\frac{1}{{{{v}_{n}}}}} \right]
The wavelength of the wave associated with a moving particle is equal to Planck’s quantum constant divided by the momentum of the particle.
Also The number of de-Broglie waves associated with \displaystyle {{n}^{{th}}} orbital electron is n.
Relation of de-Broglie wavelength with different physical quantities
Relation between de-Broglie wavelength and kinetic energy of particle:
We know that the kinetic energy E is related to linear momentum p as
E=\frac{{{{p}^{2}}}}{{2m}}
hence p=\sqrt{{2mE}}
therefore \lambda =\frac{h}{p}=\frac{h}{{\sqrt{{2mE}}}}
Relation between de-Broglie wavelength and potential difference V :
When a charged particle (q) is accelerated through a potential difference V its kinetic energy E is given by
E=Vq
we have seen in previous case \lambda =\frac{h}{{\sqrt{{2mE}}}} putting E into it we get
\lambda =\frac{h}{{\sqrt{{2mVq}}}} here \frac{h}{{\sqrt{{2mq}}}}=\text{constant}(k)
hence \lambda =\frac{k}{{\sqrt{V}}},
the value of constant k depends on the charged particle.
for example for electron
m= \displaystyle 9.1\times {{10}^{{-31}}}~kg and q= \displaystyle 1.6\times {{10}^{{-19}}}C
hence k=\frac{h}{{\sqrt{{2mq}}}}=\frac{{6.6\times {{{10}}^{{-34}}}}}{{\sqrt{{2\times 9.1\times {{{10}}^{{-31}}}\times 1.6\times {{{10}}^{{-19}}}}}}}=12.27\times {{10}^{{-10}}}
therefore \lambda =\frac{{12.27\times {{{10}}^{{-10}}}}}{{\sqrt{V}}}meter
or \lambda =\frac{{12.27}}{{\sqrt{V}}}{{A}^{o}} ( For electron)
In the similar way you can find for proton or alpha particle etc.
Relation between de-Broglie wavelength and temperature for thermal neutron:
For thermal neutron the kinetic energy at ordinary temperature is given as
E= \displaystyle {{k}_{b}}T where \displaystyle {{k}_{b}} is the boltzman constant.
as discussed in point no.(i) \lambda =\frac{h}{p}=\frac{h}{{\sqrt{{2mE}}}} lets put E=kbT
we get \lambda =\frac{h}{{\sqrt{{2m{{k}_{b}}T}}}}.
Characteristics of Matter Waves
(1) de-Broglie or Matter wave represents the probability of finding a particle in space.
(2) de-Broglie or Matter waves are not electromagnetic in nature. Also Matter waves can propagate in vacuum, hence they are not mechanical waves.
(3) de-Broglie or matter wave is associated with every moving particle (whether charged or uncharged).
(4) Practical observation of matter waves is possible only when the de-Broglie wavelength is of the order of the size of the particles.
(5) The phase velocity of the matter waves can be greater than the speed of the light.
(6) Electron microscope works on the basis of de-Broglie waves.
Illustration:
Find the de Broglie wavelengths of (a) a 46-g golf ball moving with a speed of 30 m/s, and (b) an electron moving with a speed of \displaystyle {{10}^{{7}}} m/s.
Solution:
(a) Since v << c, we can let m = \displaystyle {{m}_{0}}.
Hence \displaystyle \lambda = \frac{\mathbf{h}}{{\mathbf{mv}}}\,=\,\frac{{\mathbf{6}\mathbf{.63}\,\times \,\mathbf{1}{{\mathbf{0}}^{{-\mathbf{34}}}}\mathbf{Js}}}{{\mathbf{(0}\mathbf{.046}\,\,\mathbf{kg)}\,\,\mathbf{(30}\,\,\,\mathbf{m/s)}}} = \displaystyle 4.8\times {{10}^{{-34}}} m
The wavelength of the golf ball is so small compared with its dimensions that we would not except to find any wave aspects in its behavior.
(b) Again v << c, so with m = \displaystyle {{m}_{0}} = \displaystyle 9.1\times {{10}^{{-31}}} kg, we have
\displaystyle \lambda = \frac{\mathbf{h}}{{\mathbf{mv}}}\,=\,\frac{{\mathbf{6}\mathbf{.63}\,\times \,\mathbf{1}{{\mathbf{0}}^{{-\mathbf{34}}}}\,\mathbf{J}\mathbf{.s}}}{{\mathbf{(9}\mathbf{.1}\,\times \,\mathbf{1}{{\mathbf{0}}^{{-\mathbf{31}}}}\mathbf{kg)}\,\mathbf{(1}{{\mathbf{0}}^{\mathbf{7}}}\mathbf{m/s)}}} = \displaystyle 7.3\times {{10}^{{-11}}} m
The dimensions of atoms are comparable with this figure – the radius of the hydrogen atom, for instance is \displaystyle 5.3\times {{10}^{{-11}}} m. It is therefore not surprising that the wave character of moving electrons is the key to understanding atomic structure and behavior.
Illustration
Find de-Broglie wavelength of 2 MeV proton. Mass of proton = \displaystyle 1.64\times {{10}^{{-27}}} kg, h = \displaystyle 6.625\times {{10}^{{-34}}} Js.
Solution
Energy of Proton,
E = 2 MeV = \displaystyle 2\times 1.6\times {{10}^{{-31}}}J
we know De-Broglie wave-length, \displaystyle \lambda =\frac{h}{p}=\frac{h}{{\sqrt{{2mE}}}}
\displaystyle \lambda =\frac{{6.625\times {{{10}}^{{-34}}}}}{{\sqrt{{2\times 1.64\times {{{10}}^{{-27}}}\times 2\times 1.6\times {{{10}}^{{-31}}}}}}}
or
\displaystyle \lambda =2.044\times {{10}^{{-14}}}m
Illustration
An electron is accelerated by a potential difference of 25 volt. Find the de-Broglie wavelength associated with it.
Solution
For an electron, de-Broglie wavelength is given by,
\displaystyle \lambda =\sqrt{{\frac{{150}}{V}}}=\sqrt{{\frac{{150}}{{25}}}}=\sqrt{6} \displaystyle \approx 2.5{\AA}
Illustration
Find the ratio of de-Broglie wavelength of a a-particle to that of a proton being subjected to the same magnetic field so that the radii of their path are equal to each other. Assume that the magnetic field induction vector \overrightarrow{B} is perpendicular to the velocities of the particles.
Solution
When a charged particle (charge q, mass m) enters perpendicularly in a magnetic field (B) than, radius of the path described by it r=\frac{{mv}}{{qB}}\Rightarrow mv=qBr.
Also de-Broglie wavelength \lambda =\frac{h}{{mv}}
Þ \lambda =\frac{h}{{qBr}} \Rightarrow \frac{{{{\lambda }_{\alpha }}}}{{{{\lambda }_{p}}}}=\frac{{{{q}_{p}}{{r}_{p}}}}{{{{q}_{\alpha }}{{r}_{\alpha }}}}=\frac{1}{2}
Illustration
Which of the following figure represents the variation of particle momentum and the associated de-Broglie wavelength
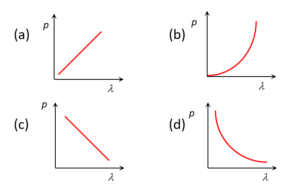
Solution
Since \displaystyle \lambda =\frac{h}{p}
or \displaystyle p=\frac{h}{\lambda }\text{ hence p}\propto \frac{1}{\lambda }therefore the graph must be a hyperbola i.e. (d).
Illustration
Find the ratio of de-Broglie wavelengths of molecules of hydrogen and helium which are at temperature \displaystyle {{27}^{o}}C and \displaystyle {{127}^{o}}C respectively.
Solution
de-Broglie wavelength \lambda =\frac{h}{{m{{v}_{{rms}}}}}, rms velocity of a gas particle at the given temperature (T) is given as
\frac{1}{2}mv_{{rms}}^{2}=\frac{3}{2}kT
\Rightarrow {{v}_{{rms}}}=\sqrt{{\frac{{3\,kT}}{m}}}
\Rightarrow m{{v}_{{rms}}}=\sqrt{{3\,mk\ T}}
or \lambda =\frac{h}{{m{{v}_{{rms}}}}}=\frac{h}{{\sqrt{{3\,mkT}}}}
\Rightarrow \frac{{{{\lambda }_{H}}}}{{{{\lambda }_{{He}}}}}=\sqrt{{\frac{{{{m}_{{He}}}{{T}_{{He}}}}}{{{{m}_{H}}{{T}_{H}}}}}}=\sqrt{{\frac{{4\,(273+127)}}{{2\,(273+27)}}}}=\sqrt{{\frac{8}{3}}}
Practice Questions (Basic Level)
1.
A photon of frequency v has a momentum associated with it. If c is the velocity of light, this momentum is
(a) \frac{{hv}}{{{{c}^{\mathbf{2}}}}}
(b) \frac{{hv}}{c}
(c) \frac{v}{c}
(d) hvc
Ans (b)
2.
The de Broglie wavelength of thermal neutrons at ordinary temperature T K is
(a) \frac{{30.8}}{{\sqrt{T}}}\text{{ }\!\!\mathrm{\AA}\!\!\text{ }}
(b) \frac{{28.7}}{{\sqrt{T}}}\text{{ }\!\!\mathrm{\AA}\!\!\text{ }}
(c) \frac{{10.1}}{{\sqrt{T}}}\text{{ }\!\!\mathrm{\AA}\!\!\text{ }}
(d) \frac{{20.2}}{{\sqrt{T}}}\text{{ }\!\!\mathrm{\AA}\!\!\text{ }}\text{.}
Ans (a)
3.
The momentum of an X-ray photon of wavelength 0.10 nm will be
(a) 6.62 x 10-34 kg-m/s
(b) 3.31 x 10-24 kg-m/s
(c) 3.31 x 10-34 kg-m/s
(d) 6.62 x 10-24 kg-m/s
Ans (d)
4.
If E1, E2 and E3 are there respective kinetic energies of an electron, an alpha particle and a proton each having the same de Broglie wavelength, then
(a) {{E}_{1}}>{{E}_{3}}>{{E}_{2}}
(b) {{E}_{2}}>{{E}_{3}}>{{E}_{1}}
(c) {{E}_{1}}>{{E}_{2}}>{{E}_{3}}
(d) {{E}_{1}}={{E}_{2}}={{E}_{3}}.
Ans (a)
5.
The de Broglie wavelength of an atom of mass m at absolute temperature T is
(a) \frac{h}{{mkT}}
(b) \frac{h}{{\sqrt{{2mkT}}}}
(c) \frac{h}{{\sqrt{{3mkT}}}}
(d) \frac{h}{{3mkT}}.
Ans (c)
Practice Questions (JEE Main Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
