Video Lecture
Theory For Making Notes
Prism
A prism has two plane surfaces inclined to each other. The angle between the surfaces is called angle of prism. It can be noted that the angle of deviation suffered by light at the first surface AB is not cancelled out by the deviation at the second surface AC, but it is added to it. Hence the net deviation of emergent light with respect to the incident light is \displaystyle \delta
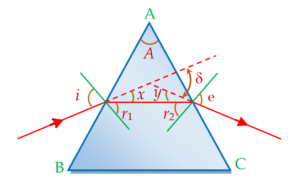
From the figure it can be observed that
\displaystyle i=x+{{r}_{1}} and \displaystyle e=y+{{r}_{2}}
on adding the equation we get
\displaystyle i+e=x+y+{{r}_{1}}+{{r}_{2}} … (i)
Also it may be noted that
\displaystyle \delta =x+y and \displaystyle A={{r}_{1}}+{{r}_{2}}
on adding the equations, we get
\displaystyle A+\delta =x+y+{{r}_{1}}+{{r}_{2}} … (ii)
Hence from equation (i) and (ii) we can conclude that
\displaystyle i+e=A+\delta
Angle of minimum deviation
As \displaystyle \delta =i+e-A hence for \displaystyle \delta to be minimum \displaystyle \frac{{d\delta }}{{di}} should be zero.
since \displaystyle \frac{{d\delta }}{{di}}=1+\frac{{de}}{{di}}-0
hence \displaystyle 1+\frac{{de}}{{di}}=0 hence \displaystyle \frac{{de}}{{di}}=-1
de = – di on integrating we get
e = – i
hence for minimum deviation it is necessary that magnitude of i and e should be same. In such a situation angle \displaystyle {{r}_{1}} and \displaystyle {{r}_{2}} will also become equal.
Since \displaystyle A={{r}_{1}}+{{r}_{2}}=2{{r}_{1}}
\displaystyle {{r}_{1}}=A/2 from \displaystyle \delta =i+e-A
but at the time of minimum deviation i = e in magnitude
hence \displaystyle {{\delta }_{m}}=\text{ }2i-A
or \displaystyle i=\frac{{A+{{\delta }_{m}}}}{2}
Using snells’s law
\displaystyle \mu =\frac{{\sin i}}{{\sin {{r}_{1}}}}, on putting the values of i and r
we get \displaystyle \mu =\frac{{\sin \left( {\frac{{A+{{\delta }_{m}}}}{2}} \right)}}{{\sin \left( {\frac{A}{2}} \right)}}
Deviation of light produced by a prism of small angle
If angle of prism A is small, \displaystyle {{r}_{1}} and \displaystyle {{r}_{2}} (as \displaystyle A={{r}_{1}}+{{r}_{2}}) and hence i and e will also be small.
Applying Snell’s law on first surface
\displaystyle \mu =\frac{{\sin i}}{{\sin {{r}_{1}}}} or \displaystyle \sin i=\mu \times \sin {{r}_{1}}
Since for small angles in \displaystyle sin\theta =\theta , hence \displaystyle i=\text{ }\mu {{r}_{{1}}}.
Similarly on second surface
\displaystyle \frac{1}{\mu }=\frac{{\sin {{r}_{2}}}}{{\sin e}}
or \displaystyle e=\text{ }\mu {{r}_{{2}}}
So on adding we gat
\displaystyle \left( {i+e} \right)=\mu \left( {{{r}_{1}}+{{r}_{2}}} \right)
Snell’s law at first and second surfaces of prism gives respectively:
therefore \displaystyle \left( {i+e} \right)~=\mu A
[because \displaystyle A={{r}_{1}}+{{r}_{2}}]
So for small angle of prism, applying equation
\displaystyle i+e=A+\delta
or \displaystyle \delta =i+e-A
or \displaystyle \delta =\mu A-A,
i.e. \displaystyle \delta =\left( {\mu-1} \right)A [where \displaystyle A={{r}_{1}}+{{r}_{2}}]
Important Points
The deviation produced by a prism depends on angle of incidence i, angle of prism A, \displaystyle \mu of the material of the prism and wavelength of light \displaystyle \lambda . So
(1)
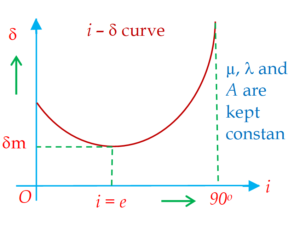
For a given value of A, material of prism and wavelength , as angle of incidence increases, angle of deviation first decreases, reaches a minimum and then increases, as shown in figure.
(2)
For a given material of prism, light and angle of incidence, as angle of prism increases, angle of deviation also increases, i.e.
\displaystyle \delta \propto A
Special cases related with prism
Condition of No emergence
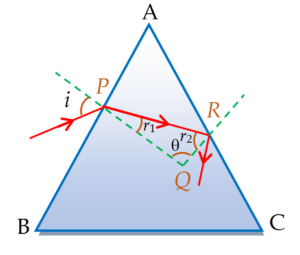
The light will not emerge out of a prism for all values of angle of incidence if at face AB for i = max = \displaystyle 90{}^\circ ,
at face AC
\displaystyle {{r}_{2}}>{{\theta }_{C}} (where \displaystyle {{\theta }_{C}} is the critical angle) … (i)
Now from Snell’s law at face AB, we have
\displaystyle {1\text{ }\times \text{ }sin\text{ }90{}^\circ \text{ }=\text{ }\mu \text{ }sin{{r}_{1}}}
Hence \displaystyle {{{r}_{1}}=\text{ }si{{n}^{{1}}}\left( {1/\mu } \right)}
or \displaystyle {{r}_{1}}={{\theta }_{C}} … (ii)
So from equations (i) and (ii)
\displaystyle {{r}_{1}}+{{r}_{2}}>2{{\theta }_{C}} … (iii)
However, in a prism
\displaystyle {{r}_{1}}+{{r}_{2}}=A … (iv)
So from equations (iii) and (iv)
\displaystyle {A>2{{\theta }_{C}}} … (v)
or \displaystyle {\left( {A/2} \right)>sin{{\theta }_{C}}}
i.e. \displaystyle {\mu >\cos ec\frac{A}{2}} … (vi)
Hence a ray of light will not emerge out of a prism (whatever be the angle of incidence) if \displaystyle {A>2{{\theta }_{C}}} i.e. if \displaystyle {\mu >\cos ec\frac{A}{2}}.
Condition of Grazing emergence
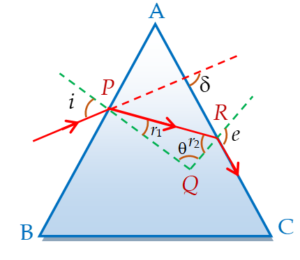
If a ray can emerge out of a prism, the value of angle of incidence i for which angle of emergence \displaystyle e=90{}^\circ is called condition of grazing emergence.
In this situation as the ray emerges out of face AC, i.e., TIR does not take place at it,
\displaystyle {{{r}_{2}}<{{\theta }_{C}}} … (i)
But as in a prism \displaystyle A={{r}_{1}}+{{r}_{2}}
So \displaystyle {{r}_{1}}=A-{{\theta }_{C}} … (ii)
Now from Snell’s law at face AB, we have
\displaystyle 1\text{ }sini=\text{ }\mu \text{ }sin{{r}_{1}}
which in the light of equation (ii) gives
\displaystyle sini>\mu \text{ }sin(A-{{\theta }_{C}})
i.e. \displaystyle sini>\mu \text{ }[sinAcos{{\theta }_{C}}-\text{ }cosAsin{{\theta }_{C}}]
i.e. \displaystyle \sin i>\mu [(\sin A)\sqrt{{(1-{{{\sin }}^{2}}{{\theta }_{C}})}}-\cos A\sin {{\theta }_{C}}]
\displaystyle [as\text{ }sin{{\theta }_{C}}\text{= }\left( {1/\mu } \right)]
Hence \displaystyle \sin i>[\sqrt{{({{\mu }^{2}}-1)}}\sin A-\cos A]
or \displaystyle i>{{\sin }^{{-1}}}[\sqrt{{({{\mu }^{2}}-1)}}\sin A-\cos A]
or \displaystyle {{(i)}_{{\min }}}={{\sin }^{{-1}}}[\sqrt{{({{\mu }^{2}}-1)}}\sin A-\cos A] … (iii)
i.e. light will emerge out of prism only if angle of incidence is greater than \displaystyle {{\left( i \right)}_{{min}}} given by equation (iii). In this situation deviation will be given by \displaystyle \delta =i+90{}^\circ -A with i given by equation (iii).
Maximum deviation
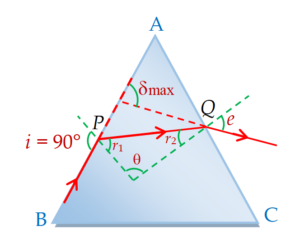
Deviation will be maximum when angle of incidence i is maximum, i.e., \displaystyle {\text{i=}90{}^\circ }, so equation
\displaystyle \delta =i+e-A with \displaystyle A={{r}_{1}}+{{r}_{2}}
reduce to
\displaystyle {{\delta }_{{max}}}=\text{ }90{}^\circ \text{ }+e\text{ }\text{ }-A … (i)
However, when \displaystyle {\text{i=}90{}^\circ } .
Hence using Snell’s law we get
\displaystyle {1\times sin90{}^\circ =\mu \text{ }sin{{r}_{1}}}
i.e. \displaystyle {{r}_{1}}=\text{ }si{{n}^{{1}}}\left( {1/\mu } \right) or \displaystyle {{r}_{1}}={{\theta }_{C}}
and as in a prism \displaystyle A={{r}_{1}}+{{r}_{2}}, hence \displaystyle {{r}_{2}}=\text{ }A-{{\theta }_{C}}
So at surface AC,
\displaystyle {1\times \sin e=\mu \text{ }sin{{r}_{2}}} ,
i.e. \displaystyle sine=\text{ }\mu \text{ }sin\text{ }(A-{{\theta }_{C}})
or \displaystyle e=\text{ }si{{n}^{{1}}}[\mu \text{ }sin\text{ }(A-{{\theta }_{C}})] … (ii)
So equation (i) gives maximum deviation while (ii) angle of emergence in condition of maximum deviation, i.e. \displaystyle i=90{}^\circ . The situation is reverse of grazing emergence, i.e., it may also be viewed as deviation at grazing incidence.
Dispersion of Light
When white light passes through a prism it splits up into constituent colors. This phenomenon is called dispersion and this arise due to the fact that refractive index of a prism is different for different wavelengths. So different wavelengths in passing through a prism are deviated through different angles and from relation \displaystyle \delta =\left( {\mu-1} \right)A , we can see that violet is deviated most ( because \displaystyle \mu for violet is maximum) while for red it is least ( because \displaystyle \mu for red is minimum) this give rise to display of colors known as spectrum. Rainbow, the most colorful phenomenon in nature, is primarily due to the dispersion of sunlight by rain-drops suspended in air .
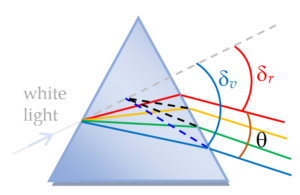
dispersive power \displaystyle \omega
\displaystyle \omega =\frac{\theta }{\delta }=\frac{{{{\delta }_{V}}-{{\delta }_{R}}}}{\delta } … (i)
But as for a prism,
\displaystyle \delta =(\mu -1)A,
\displaystyle \omega =\frac{{{{\mu }_{V}}-{{\mu }_{R}}}}{{(\mu -1)}}=\frac{{d\mu }}{{(\mu -1)}} … (ii)
From expressions (i) and (ii) it is clear that dispersive power like refractive index has no units and dimensions and depends on the material of the prism.
Dispersion without deviation
As angle of deviation depends upon the prism material, we are in a position to put together prisms of different materials in such a way that the net outcome is such that while dispersion remains, deviations get cancelled out.
One such combination is when 3 crown glass prisms are combined with 2 flint glass prisms are shown in the figure.
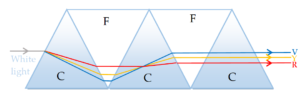
This can be done when deviation \displaystyle {{\delta }_{1}} produced by first prism is equal and opposite to the deviation \displaystyle {{\delta }_{2}} produced by the second prism.
\displaystyle {{\delta }_{1}}=({{\mu }_{1}}-1){{\text{A}}_{1}}
\displaystyle {{\delta }_{2}}=({{\mu }_{2}}-1){{\text{A}}_{2}}
So, for nil resultant deviation,
\displaystyle {{\delta }_{1}}+{{\delta }_{2}}=0
or, \displaystyle ({{\mu }_{1}}-1)\ {{\text{A}}_{1}}+({{\mu }_{2}}-1){{\text{A}}_{2}}=0
If \displaystyle {{\mu }_{1}} and \displaystyle {{\mu }_{2}} are the refractive indices of two prisms for yellow (i.e. mean) light and \displaystyle {{A }_{1}} and \displaystyle {{A }_{2}} are their angles, then the condition that these two prisms (one each type) will produce dispersion without deviation is
\displaystyle \frac{{\text{A}{{}_{1}}}}{{{{\text{A}}_{2}}}}=-\frac{{({{\mu }_{2}}-1)}}{{({{\mu }_{1}}-1)}}
Deviation without dispersion
We can also select angles and materials of the two prisms in such a way as to produce deviation without dispersion.
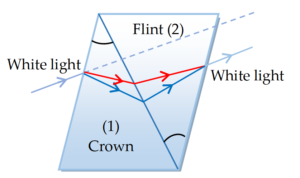
If \displaystyle {{\delta }_{1}} and \displaystyle {{\delta }_{2}} are the deviation the deviation suffered by the mean (i.e. yellow) light ray in 1st and 2nd prism, then the following is the condition to get deviation without dispersion.
\displaystyle {\frac{{{{\omega }_{1}}}}{{{{\omega }_{2}}}}=-\frac{{{{\delta }_{2}}}}{{{{\delta }_{1}}}}}
where \displaystyle {{\omega}_{1}} and \displaystyle {{\omega }_{2}} are the respective dispersive powers and (–) sign indicates that the two prisms should be combined in an inverted manner.
Illustration
A glass prism of angle \displaystyle 72{}^\circ and index of refraction 1.66 is immersed in a liquid of refractive index 1.33. Find the angle of minimum deviation for a parallel beam of incident light passing through the prism.
Solution
Here as \displaystyle \mu =\left( {{{\mu }_{G}}/{{\mu }_{L}}} \right)= (1.66/1.33) therefore in the position of minimum deviation,
\displaystyle \mu =\frac{{\sin [(A+{{\delta }_{m}})/2]}}{{\sin (A/2)}}
i.e. \displaystyle \sin \frac{{(A+{{\delta }_{m}})}}{2}=\mu \sin \frac{A}{2}
So \displaystyle \sin \left[ {\frac{{72{}^\circ +{{\delta }_{m}}}}{2}} \right]=\frac{{1.66}}{{1.33}}\sin \left[ {\frac{{72{}^\circ }}{2}} \right]
i.e. \displaystyle sin\text{ }[72{}^\circ \text{ }+{{\delta }_{m}})/2]= 1.248 × 0.5878 = 0.7336
or \displaystyle 72{}^\circ \text{ }+{{\delta }_{m}}=\text{ }2\text{ }si{{n}^{{1}}}\left( {0.7336} \right)\text{ }
\displaystyle =2\times 47.19{}^\circ
or \displaystyle {{\delta }_{m}}=94.37{}^\circ 72{}^\circ =22.37{}^\circ
Illustration
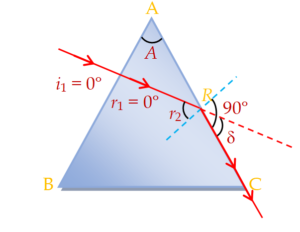
A ray of light falls normally on a refracting face of a prism of refractive index 1.5. Find the angle of the prism if the ray just fails to emerge from the prism.
Solution
A first face of the prism as \displaystyle {{i}_{1}}=0{}^\circ ~,
\displaystyle sin0{}^\circ =1.5{{r}_{1}},
i.e. \displaystyle {{r}_{1}}=0{}^\circ
And as for a prism,
\displaystyle A={{r}_{1}}+{{r}_{2}} so \displaystyle A={{r}_{2}} … (i)
But at second face, as the ray just fails to emerge, i.e.,
\displaystyle {{r}_{2}}={{\theta }_{C}}
So from equation (i) and (ii),
\displaystyle {{r}_{2}}=A={{\theta }_{C}}
But as
\displaystyle {{\theta }_{C}}={{\sin }^{{-1}}}\left[ {\frac{1}{\mu }} \right]={{\sin }^{{-1}}}\left[ {\frac{2}{3}} \right]=42{}^\circ
so, A = \displaystyle 42{}^\circ
Illustration
Let ABC represents an equiangular prism. Light of a given frequency falls on face AB, gets refracted and travels parallel to the base of prism. White emerging from face AC, the ray deviates by an angle 30°. Find the refractive index of the materials of prism.
Solution
Since the prism is placed in the minimum deviation position so From simple geometric considerations we can say that
\displaystyle {{r}_{1}}=30{}^\circ and \displaystyle {{r}_{2}}=30{}^\circ
Because \displaystyle {{r}_{1}}={{r}_{2}}, \displaystyle {{i}_{1}}={{i}_{2}}.
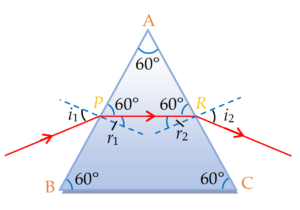
Now, the ray suffers a deviation \delta= \displaystyle 30{}^\circ at face AC,
Where \displaystyle \delta={{i}_{2}}-{{r}_{2}}
therefore \displaystyle {{{i}_{2}}-{{r}_{2}}=\text{ }30{}^\circ }
or \displaystyle {{i}_{2}}=30{}^\circ +30{}^\circ ~~~\left[ {{{r}_{2}}=30{}^\circ } \right]
Hence \displaystyle {{i}_{2}}=60{}^\circ
Because \displaystyle {{{i}_{1}}={{i}_{2}}}
hence \displaystyle {{i}_{1}}=60{}^\circ
Now apply Snell’s law as face AB
\displaystyle \mu =\frac{{\sin {{i}_{1}}}}{{\sin {{r}_{1}}}}=\frac{{\sin 60{}^\circ }}{{\sin 30{}^\circ }}=\frac{{\sqrt{3}/2}}{{1/2}}=\sqrt{3}
Illustration
A ray of light incident at \displaystyle 49{}^\circ on the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism.
Solution
As the prism is an equilateral one, A = \displaystyle 60{}^\circ °. As the ray of light passes symmetrically, the prism is in the position of minimum deviation.
So, r = \frac{A}{2} = \frac{{60{}^\circ }}{2}\,=\,30{}^\circ
also, i = \displaystyle 49{}^\circ ,
therefore \displaystyle \mu = \frac{{\sin \,i}}{{\sin \,r}}\,=\,\frac{{\sin \,49{}^\circ }}{{\sin \,30{}^\circ }}\,=\,\frac{{0.7547}}{{0.5}} = 1.5
Illustration
The refracting angle of the prism is \displaystyle 60{}^\circ and the refractive index of the material of the prism is 1.632. Calculate the angle of minimum deviation.
Solution
Here, A = 60°; \displaystyle \mu = 1.632
Now, \displaystyle \mu = \frac{{\sin \,\,(\frac{{A\,+\,{{\delta }_{m}}}}{2})}}{{\sin \,(\frac{A}{2})}}
or, 1.632 = \frac{{\sin \,(\frac{{60{}^\circ \,+\,{{\delta }_{m}}}}{2})}}{{\sin \,\frac{{60{}^\circ }}{2}}}\,=\,\frac{{\sin \,(\frac{{60\,+\,{{\delta }_{m}}}}{2})}}{{\sin \,30{}^\circ }}
or, sin \left( {\frac{{60{}^\circ +{{\delta }_{m}}}}{2}} \right) = 1.632 sin \displaystyle 30{}^\circ = 1,632 × 0.5
or, sin \left( {\frac{{60{}^\circ +{{\delta }_{m}}}}{2}} \right) = 0.816
or, \frac{{60{}^\circ +{{\delta }_{m}}}}{2} = \displaystyle 5\mathbf{4}{}^\circ 4\mathbf{2}’
\displaystyle {{\delta }_{m}}=\mathbf{49}{}^\circ \mathbf{24}’
Illustration
Find the minimum and maximum angle of deviation for a prism with angle A = \displaystyle 60{}^\circ and \displaystyle \mu = 1.5.
Solution
Minimum deviation:
The angle of minimum deviation occurs when i = e and \displaystyle {{r}_{1}}={{r}_{2}} and is given by
\displaystyle \mu = \frac{{\sin \,(A\,+\,{{\delta }_{m}})/2}}{{\sin \,\frac{A}{2}}}
or \displaystyle {{\delta }_{m}}=2si{{n}^{{-1}}}(\mu sin \frac{A}{2}) – A
Substituting \displaystyle \mu = 1.5 and A = \displaystyle \text{6}0{}^\circ ,
we get \displaystyle {{\delta }_{m}}=2\text{ }si{{n}^{{1}}}\left( {0.75} \right)60{}^\circ
\displaystyle {{\delta }_{m}}=37{}^\circ
Maximum deviation:
The deviation is maximum when \displaystyle i=e=90{}^\circ that is at grazing incidence or grazing emergence.
when \displaystyle i=90{}^\circ , then \displaystyle {{r}_{1}} = \displaystyle{{\theta}_{C}}
Hence \displaystyle {{r}_{1}}= {{sin}^{-1}} \left( {\frac{1}{\mu }} \right)
or \displaystyle {{r}_{2}}= {{sin}^{-1}}\left( {\frac{2}{3}} \right)
= \displaystyle 42{}^\circ
or \displaystyle {{r}_{2}}=A-{{r}_{1}}
= \displaystyle \text{6}0{}^\circ -42{}^\circ =18{}^\circ
Using \frac{{\sin \,{{r}_{2}}}}{{\sin \,e}}\,=\,\frac{1}{\mu }, we have
\displaystyle sine=\mu sin{{r}_{2}}
\displaystyle sine=1.5\text{ }\times \text{ }sin\text{ }18{}^\circ
or sin e = 4.63
or e = \displaystyle 28{}^\circ
hence Deviation = \displaystyle {{\delta }_{{max}}}=\left( {i+e} \right)A
hence \displaystyle {{\delta }_{{max}}}=90{}^\circ +28{}^\circ 60{}^\circ =\mathbf{58}{}^\circ
Illustration
A prism having a refracting angle \displaystyle 4{}^\circ and refractive index 1.5 is located in front of a vertical plane mirror as shown. A horizontal ray of light is incident on the prism. What is the angle of incidence at the mirror?
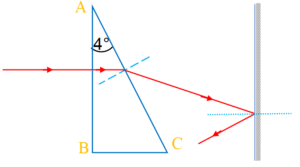
Solution
The deviation suffered by refraction through the small angled prism is given by
\displaystyle \delta =\left( {\mu – 1} \right)A = (1.5 – 1) × \displaystyle 4{}^\circ
hence \displaystyle \delta={{2}^{o}}
This gives the angle of incidence \displaystyle 2{}^\circ at the mirror.
Illustration
Calculate the dispersive power of crown and flint glass-prism from the following data For crown glass
\displaystyle {{\mu }_{v}}= 1.522 ;
\displaystyle {{\mu }_{r}} = 1.514
For flint glass
\displaystyle {{\mu }_{v}}= 1.662 ;
\displaystyle {{\mu }_{r}} = 1.644
Solution
For crown glass
\displaystyle {{\mu }_{v}}= 1.522 ;
\displaystyle {{\mu }_{r}} = 1.514
for mean ray \displaystyle \mu = \frac{{{{\mu }_{V}}+{{\mu }_{R}}}}{2}\,=\,\frac{{1.522\,+\,1.514}}{2}\,=\,1.518
Hence, the dispersive power of crown glass
\displaystyle \omega = \frac{{{{\mu }_{V}}-{{\mu }_{r}}}}{\mu -1}\,=\,\frac{{1.522-1.514}}{{1.518}} = 0.00527
For flint glass
\displaystyle {{\mu }_{v}}= 1.662 ;
\displaystyle {{\mu }_{r}} = 1.644
for mean ray \displaystyle \mu = \frac{{{{\mu }_{V}}+{{\mu }_{R}}}}{2}\,=\,\frac{{1.662\,+\,1.644}}{2}\,= 1.653
\displaystyle \omega = \frac{{{{\mu }_{v}}-{{\mu }_{R}}}}{{\mu -1}}\,=\,\frac{{1.662\,-\,1.644}}{{(1.653-1)}} = 0.0276
Illustration
Find the angle of a prism of dispersive power 0.021 and refractive index 1.53 to form an achromatic combination with the prism of angle \displaystyle 4.2{}^\circ and dispersive power 0.045 having refractive index 1.65. Also calculate the resultant deviation.
Solution
For first prism
\displaystyle \omega = 0.021; \displaystyle \mu = 1.53;
For second prism
\displaystyle {{\omega}^{\prime}} = 0.045; \displaystyle {{\mu}^{\prime}}= 1.65 and \displaystyle {{A}^{\prime}}={{4.2}^{o}}
For no dispersion
\displaystyle \omega \delta +{{\omega}^{\prime}}{{\delta}^{\prime}}=0
or, \displaystyle \omega (\mu -1)A+{{\omega}^{ \prime}}({{\mu}^{ \prime}} -1){{A}^{\prime}}=0
or, A = – \frac{{{{\omega}^{ \prime}} {{A}^{\prime}} \,({{\mu}^{ \prime}} -1)}}{{(\mu -1)}}\,=\,-\,\frac{{.045\,\times \,4.2\,\times \,(1.65\,-1)}}{{.021\,\times \,(1.53-1)}} = \displaystyle 11.4{}^\circ
Net deviation = \displaystyle \delta +{{\delta}^{\prime}}
= \displaystyle (\mu \text{ }-1)A+\text{ }({{\mu}^{\prime}}-\text{ }1){{A}^{\prime}}= – \displaystyle 11.4{}^\circ (1.53-1) + \displaystyle 4.2{}^\circ (1.65-1)
= – \displaystyle 3.12{}^\circ
Practice Questions (Basic Level)
Q.1
A ray of light falls normally on a refracting face of a prism of refractive index 1.5. If the ray just fails to emerge from the prism. Then the angle of prism is
(a) {{\sin }^{{-1}}}\left( {\frac{2}{3}} \right)
(b) {{\cos }^{{-1}}}\left( {\frac{2}{3}} \right)
(c) {{\sin }^{{-1}}}\left( {\frac{1}{2}} \right)
(d) {{\sin }^{{-1}}}\left( {\frac{1}{2}} \right)
Ans. (a)
Q.2
A glass prism of refractive index 1.5 is immersed in water (m = 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, if
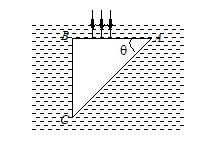
(a) \sin \theta \ge \frac{8}{9}
(b) \sin \theta \le \frac{2}{3}
(c) \sin \theta =\frac{4}{5}
(d) \frac{2}{3}<\sin \theta <\frac{8}{9}
Ans. (a)
Q.3
Light is incident normally on face AB of a prism as shown in figure. A liquid of refractive index m is placed on face AC of the prism. The prism is made of glass of refractive index 3/2. The limits of m for which total internal reflection cannot takes place on face AC is
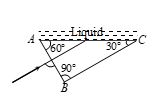
(a) \frac{{3\sqrt{3}}}{4}> m > \frac{{3\sqrt{3}}}{4}
(b) \mu <\frac{{3\sqrt{3}}}{4}
(c) \mu >\sqrt{3}
(d) \mu <\frac{{\sqrt{3}}}{2}
Ans. (b)
Q.4
A ray of light falls on a prism ABC (AB = BC) and travels as shown in figure. The refractive index of the prism material should be greater than
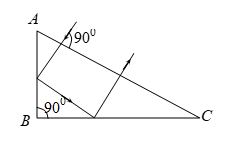
(a) 4/3
(b) \sqrt{2}
(c) 1.5
(d) \sqrt{3}
Ans. (b)
Q.5
We have two equilateral prisms A and B. They are made of materials having refractive index 1.5 and 1.6. For minimum deviation, incident angle will be
(a) small for prism A
(b) small for prism B
(c) equal for both the prisms
(d) can’t be predicted
Ans. (a)
Q.6
A light ray is incident upon a prism in minimum deviation position and suffers a deviation of 34°. If the shaded half of the prism is knocked off, the ray will
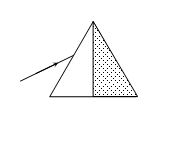
(a) Suffer a deviation of 34°
(b) Suffer a deviation of 68°
(c) Suffer a deviation of 17°
(d) Not come out of the prism
Ans. (c)
Q.7
The light ray is incident at angle of 60° on a prism of angle 45°. When the light ray falls on the other surface at 90°, the refractive index of the material of prism m and the angle of deviation d are given by
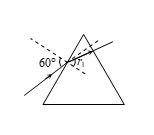
(a) \mu =\sqrt{{\frac{3}{2}}},\,\,\delta =30{}^\circ
(b) \mu =1.5,\,\,\delta =15{}^\circ
(c) \mu =\frac{{\sqrt{3}}}{2},\,\,\delta =30{}^\circ
(d) \mu =\sqrt{{\frac{3}{2}}},\,\delta =15{}^\circ
Ans. (d)
Q.8
For a material, the refractive indices for red, violet and yellow colour light are respectively 1.52, 1.64 and 1.60. The dispersive power of the material is
(a) 2 (b) 0.45 (c) 0.2 (d) 0.045
Ans. (c)
Q.9
A prism (m = 1.5) has a refracting angle of 30°. The deviation of a monochromatic ray incident normally on its one surface will be (sin48°36¢ = 0.75)
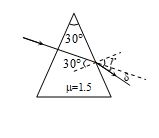
(a) 18°36¢ (b) 22°38¢ (c) 18° (d) 22°1
Ans. (a)
Practice Questions (JEE Main Level)
Q.1
A ray of light makes normal incidence on the diagonal face of a right-angled prism as shown in figure. If \displaystyle \theta = 37o then the angle of deviation is (sin 37o = 3/5)
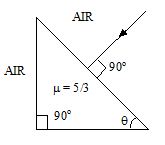
(a) 53o
(b) 127o
(c) 106o
(d) 90o
Ans (c)
Q.2
\displaystyle \eta number of identical equilateral prisms are kept in contact as shown in figure. If deviation through a single prism is \displaystyle \delta then consider the following statements (m is an integer).

(i) if ( \displaystyle \eta = 2m) deviation through \displaystyle \eta prisms is zero
(ii) if ( \displaystyle \eta = 2m +1) deviation through system of \displaystyle \eta prisms is \displaystyle \delta
(iii) if \displaystyle \eta = 2m deviation through system of \displaystyle \eta prisms is \displaystyle \delta
(iv) if \displaystyle \eta = 2m + 1 deviation through system of \displaystyle \eta prisms is zero
(a) statements (i) & (iii) are true
(b) statements (i) and (ii) are true
(c) statements (i) and (iv) are true
(d) statements (iii) and (iv) are true
Ans (b)
Q.3
Two parallel light rays pass through an isosceles prism of refractive index \sqrt{{3/2}} as shown in figure. The angle between the two emergent rays is
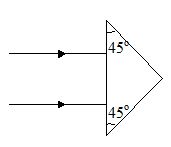
(a) 15o
(b) 30o
(c) 45o
(d) 60o
Ans (b)
Q.4
What is the minimum value of the refractive index for a 90º – 45º – 45º prism which is used to deviate a beam through 90º by total internal reflection?
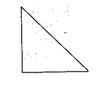
(a) 3/2
(b) \displaystyle \sqrt{3}
(c) \displaystyle \sqrt{2}
(d) 5/3
Ans (c)
Q.5
Light is incident normally on face AB of a prism as shown in figure. A liquid of refractive index \displaystyle \mu is placed on face AC of the prism. The prism is made of glass of refractive index 3/2. The limits of \displaystyle \pi for which total internal reflection takes place on face AC is
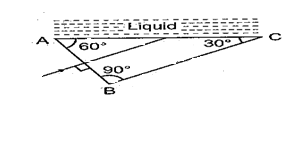
(a) \displaystyle \mu \,>\,\frac{{\sqrt{3}}}{2}
(b) \displaystyle \mu \,<\,\frac{{3\sqrt{3}}}{4}
(c) \displaystyle \mu \,<\sqrt{3}
(d) \displaystyle \mu \,<\frac{{\sqrt{3}}}{2}
Ans (b)
Q.6
A prism having refractive index \sqrt{2} and refracting angle 30o, has one of the refracting surfaces polished. A beam of light incident on the other refracting surface will trace its path if the angle of incidence is
(a) 0o (b) 30o (c) 45o (d) 60o
Ans. (c)
Q.7
A ray of light is incident at an angle i on one surface of a prism of small angle A and emerges normally from the opposite surface. If the refractive index of the material of the prism is m, the angle of incidence i is nearly equal to
(a) \frac{A}{\mu }
(b) \frac{A}{{2\mu }}
(c) mA
(d) \frac{{\mu A}}{2}
Ans. (c)
Q.8
The angle of a prism is A. Its one surface is silvered. Light rays falling at an angle of incidence 2A on first surface retrace the same path after suffering reflection at the second silvered surface. The refractive index of material is
(a) 2 sin A (b) 2 cos A (c) (1/2) cos A (d) tan A
Ans. (b)
Q.9
A thin prism P1 with angle 4° and made from glass of refractive index of 1.54 is combined with another thin prism P2 made from glass of refractive index 1.72 to produce dispersion without deviation. The angle of the prism P2 is
(a) 5.33° (b) 4° (c) 3° (d) 2.6°
Ans. (c)
Q.10
A prism can have a maximum refracting angle of (C = critical angle
(a) 60o (b) C (c) 2C (d) slightly less than 180o]
Ans. (c)
11.
A ray is incident perpendicular to one face of an equilateral prism as in figure. What is the minimum value of the refractive index required for total internal reflection at the second face?
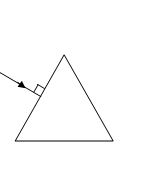
(a) 1.15
(b) 3.0
(c) 1.0
(d) 2.0
Ans (a)
Practice Questions (JEE Advance Level)
1.
In the figure shown, a ray is incident on the face ‘oa’ of the prism at an angle i. The emergent ray is parallel to the face ‘ob’. If the angle of prism is A = 30o and the refractive index µ= \displaystyle \frac{2}{{\sqrt{3}}}, then find the angle of incidence, and the angle of deviation. State whether the deviation is clockwise or anti-clockwise.
Take sin35o = \displaystyle \frac{1}{{\sqrt{3}}}
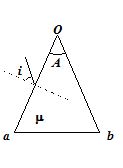
(a)25o
(b)35o
(c)50o
(d)90o
Ans (a)
2.
A ray is obliquely incident on a prism of refractive index m as shown in figure. Then the maximum value of a for which there is an emergent ray along face AC is given by
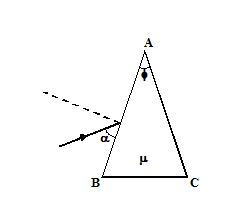
(a) \displaystyle \cos \alpha =\mu \sin (\phi -{{\theta }_{c}})
(b) \displaystyle \cos \alpha =\mu \sin (\phi +{{\theta }_{c}})
(c) \displaystyle \cos (\alpha -\phi )=\mu \sin (\phi +{{\theta }_{c}})
(d) \displaystyle \sin \alpha =\mu \cos (\phi -{{\theta }_{c}})
where Θc is the critical angle for total internal reflection.
Ans : (a)
Comprehension Based Question (3 and 4)
A prism of refracting angle 30o is coated with a thin film of transparent material of refractive index 2.2 on face AC of the prism. A light of wavelength 6600 Å is incident on face AB such that angle of incidence is 60o
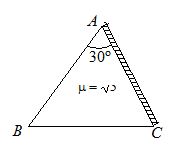
31.
The angle of emergence, and
[Given refractive index of the material of the prism is ]
(a) angle of emergence is 30
(b) angle of emergence is 50
(c) angle of emergence is 0
(d) angle of emergence is 25
Ans (c)
32.
The minimum value of thickness of the coated film on the face AC for which the light emerging from the face has maximum intensity.
(a) 1200 Å
(b) 1300 Å
(c) 1400 Å
(d) 1500 Å
Ans (d)
Comprehension Based Question (5 and 6)
Two parallel beams of light P and Q (separation d) containing radiations of wavelengths 4000Å and 5000 Å (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in the figure. The refractive index of the prism as a function of wavelength is given by the relation, m(l) = 1.20 + b/l2 where l in Å and b is positive constant. The value of b is such that the condition for total reflection at the face AC is just satisfied for one wave length and is not satisfied for the other.
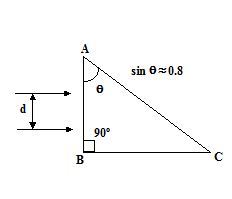
5.
Find the value of b
(a) 1.0 x 105 Å2
(b) 3.0 x 105 Å2
(c) 5.0 x 105 Å2
(d) 8.0 x 105 Å2
Ans (d)
6.
Find the deviation of the beams transmitted through the face AC
(a) 27.13o
(b) 30o
(c) 25o
(d) 25.50o
Ans (a)
7.
The cross-section of a prism is shown in the figure. One of its refracting surfaces (AC) is given by y = x2. A ray of light traveling parallel to x-axis is incident normally on face AB and refracted. Find the minimum distance of the incident ray from point A to get refracted ray from surface AC.
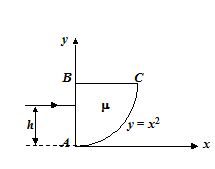
(a) h=\frac{{{{\mu }^{2}}-1}}{4}
(b) h=\frac{{{{\mu }^{3}}-1}}{5}
(c) h=\frac{{{{\mu }^{9}}-1}}{3}
(d) h=\frac{{{{\mu }^{5}}-1}}{5}
Ans (a)
