Video Lecture
Theory For Making Notes
Refration of light at plane surface
In a homogeneous medium, light rays travel in a straight line. Whenever a ray of light passes from one transparent medium to another, it gets deviated from its original path while crossing the interface of the two media (except in case of normal incidence). This phenomenon of deviation or bending of light rays from their original path while passing from one medium to another is called refraction.
In the diagram given below
AB is Incident ray.
BC is Refracted ray
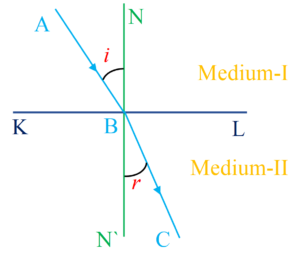
NBN’ is The normal to the refracting surface KBL at the point of incident
\displaystyle \angle i is the angle of incidence.
\displaystyle \angle r is the angle of refraction.
KL is the interface or boundary separating the two mediums.
In the second medium, the ray either bends towards the normal or away from the normal with respect to its path in the first medium.
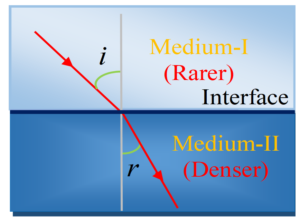
If the refracted ray bends towards the normal with respect to the incident ray, then the second medium is said to be optically denser as compared to the first medium.
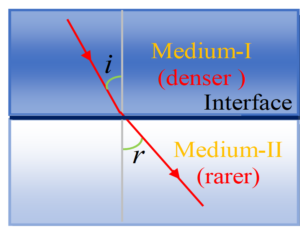
If the refracted ray bends away from the normal, then the second medium is said to be (optically) rarer as compared to the first medium.
Laws of Refraction
The phenomenon of refraction takes place according to the following two laws:
(i) The incident ray, the refracted ray and the normal to the refracting surface at the point of incidence, all lie in the same plane.
(ii) The ratio of sine of the angle of incidence to the sine of the angle of refraction is a constant for any two given media and for light of given colour.This law is called Snell’s law
If the angle of incidence and the angle of refraction be i and r respectively, then \frac{{\sin \,i}}{{\sin \,\,r}} = constant. (Snell’s law)
Some Important Points
(i)
According to Snell’s law, \frac{{\sin \,i}}{{\sin \,r}} = constant. This constant is known as refractive index (R. I.) of the second medium with respect to the first medium. It is denoted by \displaystyle _{1}{{\mu }_{2}} (or 1n2).
(ii)
Refractive index is the relative property of the two media. If the first medium carrying the incident ray is air (strictly vacuum), then the ratio \frac{{\sin \,i}}{{\sin \,\,r}} is called the absolute refractive index of the second medium. It is dented by \displaystyle \mu or n.
(iii)
According to the wave theory of light.
\displaystyle _{1}{{\mu }_{2}} = \frac{{\sin \,i}}{{\sin \,\,r}}
so \displaystyle _{1}{{\mu }_{2}}= \frac{{\text{velocity}\,\,\text{of}\,\,\text{light}\,\,\text{in}\,\,\text{medium}\,\,\text{1}}}{{\text{velocity}\,\,\text{of}\,\,\text{light}\,\,\text{in}\,\,\text{medium}\,\,\text{2}}} = \frac{{{{v}_{1}}}}{{{{v}_{2}}}}
Hence, the absolute refractive index of the medium is given by
\displaystyle \mu = \frac{{\text{velocity}\,\,\text{of}\,\,\text{light}\,\,\text{in}\,\,\text{vacuum}\,}}{{\text{velocity}\,\,\text{of}\,\,\text{light}\,\,\text{in}\,\,\text{medium}\,}}\,\,=\,\,\frac{c}{v}
(iv)
If the absolute refractive indices of the media 1 and 2 are \displaystyle {{\mu }_{1}} and \displaystyle {{\mu }_{2}} respectively,
then
\displaystyle _{1}{{\mu }_{2}} = \frac{{{{v}_{1}}}}{{{{v}_{2}}}} = \frac{{c/\,{{v}_{1}}}}{{c/{{v}_{2}}}}\,=\,\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}
(v)
We know \displaystyle _{1}{{\mu }_{2}} = \frac{{\sin \,i}}{{\sin \,\,r}}\,=\,\,\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}
or \displaystyle {{\mu }_{1}}sini = \displaystyle {{\mu }_{2}} sinr
This is the most general formula for the refraction at a surface.
(vi)
We have
\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}\,=\,\frac{{c/{{v}_{2}}}}{{c/{{v}_{1}}}}\,=\,\frac{{{{v}_{1}}}}{{{{v}_{2}}}}
or {{v}_{2}}{{µ}_{2}}={{v}_{1}}{{µ}_{1}}
or v. \mu = constant
This shows that the higher is the refractive index of a medium, lesser is the velocity of light in that medium. Thus, a medium having higher absolute refractive index is called optically denser; while the one having smaller absolute refractive index is called to be optically rarer.
(vii)
The frequency of light remains unchanged while passing from one medium to another. Hence,
\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}\,=\,\frac{{{{v}_{1}}}}{{{{v}_{2}}}}\,=\,\frac{{v{{\lambda }_{1}}}}{{v{{\lambda }_{2}}}}\,=\,\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}
(viii)
If the ray of light is incident normally on a boundary, i.e. \displaystyle \angle i = 0, then from Snell’s law
\displaystyle {{\mu }_{1}} sini = \displaystyle {{\mu }_{2}}sinr
putting i=0 we get sin r = 0
or \displaystyle \angle r = 0
Thus, light in the second medium will pass undeviated.
Principle of Reversibility of Light Rays
Any actual ray of light in an optical system, if reversed in direction, will retrace the same path backward
In simple word if a ray can travel on a path in one direction ,it can retrace the same path in the backward direction when sent backward. In the diagram given below the small mirror is used to send the light in the backward direction. This is called the principle of reversibility of light.
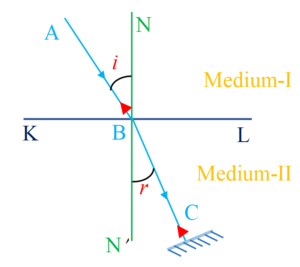
When a ray of light travels from first medium to the second medium, we have
\displaystyle _{1}{{\mu }_{2}} = \frac{{\sin \,i}}{{\sin \,\,r}} … (i)
When the path of the ray is reversed, it travels from medium-II to medium-I.
Using Snell’s Law. We have
\displaystyle _{2}{{\mu }_{1}} = \frac{{\sin \,r}}{{\sin \,i}} … (ii)
Multiplying (i) and (ii), we get,
\displaystyle _{1}{{\mu }_{2}} × \displaystyle _{2}{{\mu }_{1}} = 1
or \displaystyle _{1}{{\mu }_{2}} = \frac{1}{{_{2}{{\mu }_{1}}}}
Deviation of a ray due to Refraction
When a ray of light passes from one medium to other it deviates from its path.
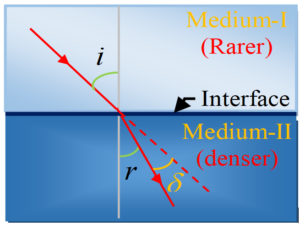
The angle of deviation is the angle between the actual path (shown by dotted red line) and the deviated path (refracted light in the diagram)
Hence \displaystyle \delta =\left| {i-r} \right|
Refraction through a glass slab
When a light ray passes through a glass slab having parallel faces, it gets refracted twice before finally emerging out of it.
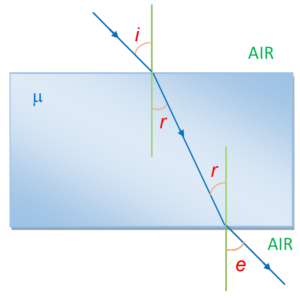
First refraction takes place from air to glass.
So \displaystyle \mu = \,\frac{{\sin \,i}}{{\sin \,\,r}} … (i)
The second refraction takes place from glass to air.
So \frac{1}{\mu }\,=\,\frac{{\sin \,r}}{{\sin \,\,e}} … (ii)
From equation (i) substitute the value of \mu in equation (ii), we get \frac{{\sin \,i}}{{\sin \,r}}\,\,=\,\,\frac{{\sin \,e}}{{\sin \,\,r}}
or i = e
Thus, the emergent ray is parallel to the incident ray.
Lateral shift in the ray while passing through the glass slab
The perpendicular distance between the incident ray and the emergent ray, when the light is incident obliquely on a parallel sided refracting glass slab is called lateral shift.
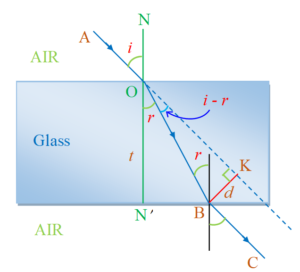
In right-angled triangle OBK, we have
\displaystyle \angle BOK = i – r
hence sin (i – r ) = \frac{d}{{OB}}
or d = OB sin (i – r) … (i)
In right angled triangle ON’B, we have
cosr = \frac{{\mathbf{{ON}^{\prime}} }}{{\mathbf{OB}}}
or OB = \frac{t}{{\cos \,r}}
Substituting the above value of OB in equation (i), we get
d = \frac{t}{{\cos \,\,r}} sin ( i – r )
Apparent Depth and Normal Shift
Case I:
When the object is in denser medium and the observer is in rarer medium (near normal incidence)
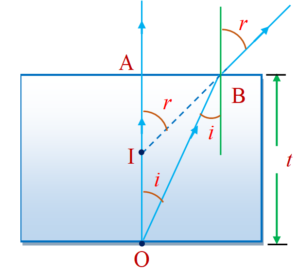
When an object O is in denser medium of depth ‘t’ and absolute refractive index \displaystyle \mu and is viewed almost normally to the surface from the outside rarer medium (say air), its image is seen at I. AO is the real depth of the object. AI is the apparent depth of the object. OI is called apparent shift.
According to Snell’s law
\frac{1}{\mu }\,=\,\frac{{\sin \,i}}{{\sin \,\,r}}
or \frac{1}{\mu }\,=\,\frac{{\tan \,i}}{{\tan \,r}} ( \because i and r are small angles)
or \displaystyle \mu = \frac{{\tan \,r}}{{\tan \,i}}
or, \displaystyle \mu = \frac{{\mathbf{AB}}}{{\mathbf{AI}}}\,\times \,\frac{{\mathbf{AO}}}{{\mathbf{AB}}}
or \displaystyle \mu = \frac{{\mathbf{AO}}}{{\mathbf{AI}}}
or \displaystyle \mu = \frac{{\text{Real}\,\,\text{depth}}}{{\text{Apparent}\,\,\text{depth}}}
Also, apparent depth = \frac{{\text{Real}\,\,\text{depth}}}{\text{ }\!\!\mu\!\!\text{ }}
hence apparent depth = \frac{t}{\mu }
and apparent shift OI is given as
OI = t – t/ \displaystyle \mu
or OI = t [1– \frac{1}{\mu }]
Case II:
When the object is in rarer medium and the observer is in denser medium (Near normal incidence).
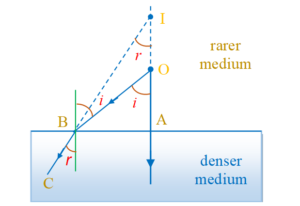
When an object O in rarer medium (say air) is seen from within a denser medium (say water), the image of O appears to be raised up to I.
The real height = AO
The apparent height = AI ; and the
Apparent shift = OI
The refraction is taking place from the rarer medium to the denser medium. So, according to Snell’s law,
\mu = \frac{{\sin \,\,i}}{{\sin \,\,r}}
or \displaystyle \mu = \frac{{\tan \,i\,}}{{\tan \,r}} ( \because I and r are small angles)
or \displaystyle \mu = \frac{{\mathbf{AB}}}{{\mathbf{AO}}}\,\,\times \,\,\frac{{\mathbf{AI}}}{{\mathbf{AB}}}
or \displaystyle \mu = \frac{{\mathbf{AI}}}{{\mathbf{AO}}}
hence \displaystyle \mu = \frac{{\text{Apparent}\,\,\text{height}}}{{\text{Real}\,\,\text{height}}}
Case III:
If a beaker is filled with immiscible transparent liquids of refracting indices, {{\mu }_{1}},{{\mu }_{2}},{{\mu }_{3}}\ldots , filled up to heights {{d}_{1}},{{d}_{2}},{{d}_{3}}\ldots respectively then the apparent depth is:
\frac{{{{d}_{1}}}}{{{{\mu }_{1}}}}+\frac{{{{d}_{2}}}}{{{{\mu }_{2}}}},\frac{{{{d}_{3}}}}{{{{\mu }_{3}}}}+\ldots
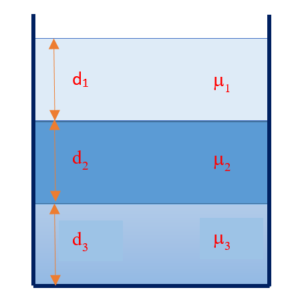
and equivalent refractive index, \text{ }\!\!\mu\!\!\text{ }=\frac{{\text{real}\ \text{depth}}}{{\text{apparent}\ \text{depth}}}=\frac{{{{d}_{1}}+{{d}_{2}}+\ldots }}{{\frac{{{{d}_{1}}}}{{{{\mu }_{1}}}}+\frac{{{{d}_{2}}}}{{{{\mu }_{2}}}}\ldots }}=\frac{{\sum{{{{d}_{i}}}}}}{{\sum{{\frac{{{{d}_{i}}}}{{{{\mu }_{i}}}}}}}}
Note: If we have two liquids of equal density i.e. \displaystyle {{d}_{1}}={{d}_{2}},
the equivalent refractive index will be given by
\displaystyle \mu =\left[ {\frac{{2{{\mu }_{1}}{{\mu }_{2}}}}{{{{\mu }_{1}}+{{\mu }_{2}}}}} \right] (i.e. harmonic mean of {{\mu}_{1}} and {{\mu}_{2}} )
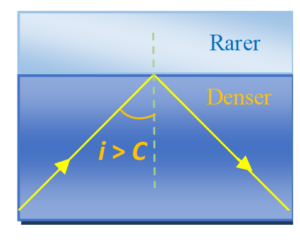
Total internal reflection
If a ray of light travelling in a denser medium strikes a rarer medium at an angle of incidence i which is greater than the critical angle C (or \displaystyle {{\theta}_{C}}), it gets totally reflected back into the same medium. This phenomenon is called as ‘total internal reflection’.
Critical angle
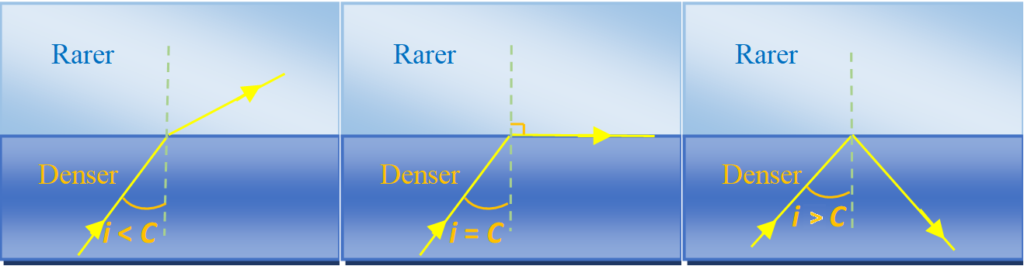
The angle of incidence for which the angle of refraction is \displaystyle {{90}^{o}} is called the critical angle for that interface. It is generally denoted by \displaystyle {{\theta}_{C}} or simply C.
Let \displaystyle {{\mu }_{R}} be the refractive index of the rarer medium and \displaystyle {{\mu }_{D}} be the refractive index of the denser medium. Obviously, \displaystyle {{\mu }_{r}} < \displaystyle {{\mu }_{D}}
From Snell’s law
\frac{{\sin \,C}}{{\sin \,\,90{}^\circ }}\,\,=\,\,\frac{{{{\mu }_{R}}}}{{{{\mu }_{D}}}}
or \frac{{\sin \,C}}{1}\,=\,\frac{{{{\mu }_{R}}}}{{{{\mu }_{D}}}}
or sinC = \frac{1}{\mu }.
where \displaystyle \mu = \frac{{{{\mu }_{D}}}}{{{{\mu }_{R}}}} is refractive index of the denser medium w.r. t. the rarer medium.
Factors on which Critical angle depends
(i)
Refractive index of two media
(ii)
Colour of light (wavelength)
(iii)
Temperature of the medium. Actually Critical angle increases
on increasing temperature.
Applications of total internal reflection
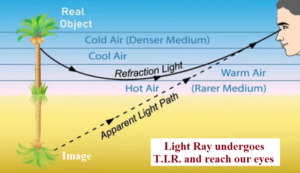
Mirage
It is caused by total internal reflection in deserts where due to heating of the earth, refractive index of air near the surface of earth becomes lesser than above it. Light from distant objects reaches the surface of earth with i > C so that total internal reflection will take place and we see the image of an object along with the object as shown in figure creating an illusion of water near the object.
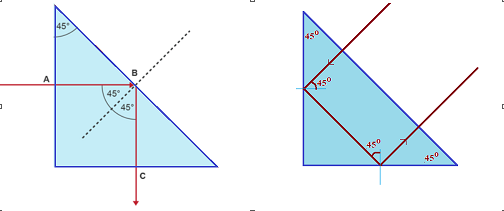
Totally reflecting prism
These prisms are \displaystyle {{45}^{o}}-{{90}^{o}}-{{45}^{o}}.They use total internal reflection to deviate the light rays at certain angles as shown below.
(a) Angle of deviation = \displaystyle {{90}^{o}}.
(b) Angle of deviation = \displaystyle {{180}^{o}}
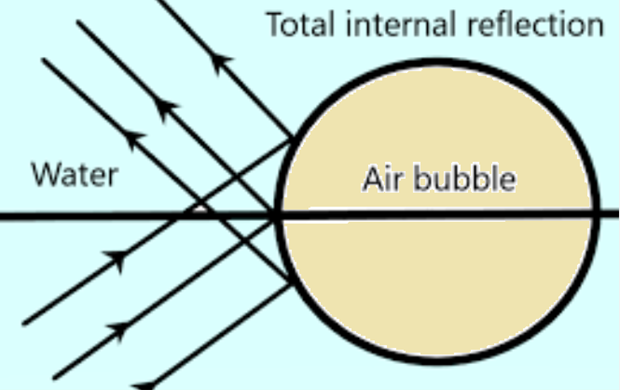
Shining of air Bubble
An air bubble in water shines due to total internal reflection at its outer surface. In this case the light propagates from denser medium (water) to rarer medium (air). If the angle of incidence is greater than the critical angle then the total internal reflection takes place and the bubble shines.
Optical fiber
It is extremely thin having a radius of few microns and long strand of very fine quality glass or quartz (Fiber core in the diagram). Each strand is coated with a thin layer of material of low refractive index so as to avoid passage of light from one fiber to the other. The refractive index of the coating material is less than that of the strand. This coating is known as cladding.
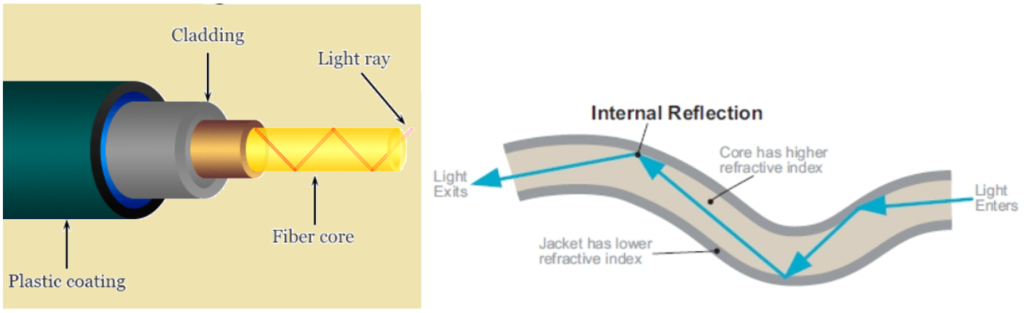
When light enters at one end of the optical fiber at a small angle, it goes inside the fiber. This light falls on the interface separating the fiber and the coating at an angle, which is greater than the critical angle. Due to multiple total internal reflections at different points the light comes out of the other end without any loss in intensity.
Uses of optical fibers
(i) They are used to transmit light without any loss in its intensity over distances of several kilometers.
(ii) They are used in the manufacture of medical instruments called endoscopes. These help the doctors to see deeply into the human body. Hence the doctor can visually examine the stomach and intestines etc. of a patient.
(iii) They are used to transmit the images of the objects.
(iv) They are used in transmitting electrical signals from another place to one with help of transducers.
(v) They are used in telecommunications for transmitting signals. A single fiber is able to transmit multiple signals (say 3000) simultaneously, without any interference, whereas the electric wire can transmit only one signal at a time.
(vi) They are used to transfer huge data because the frequency of light is about \displaystyle {{10}^{8}} times that of microwaves.
Refraction at a single spherical Convex surface
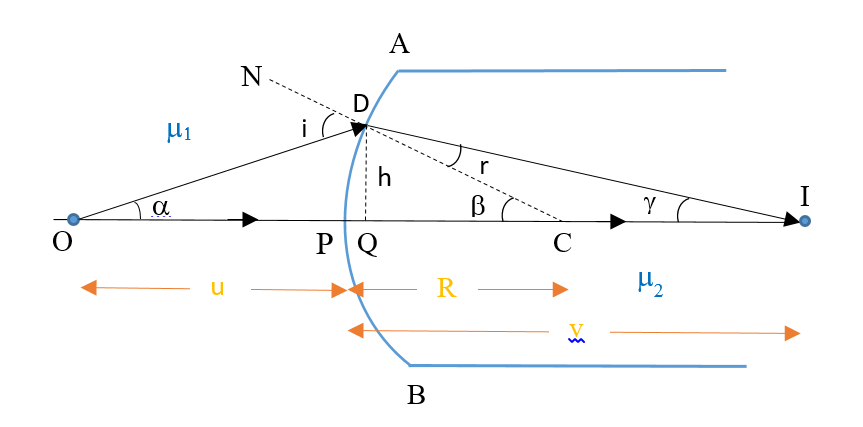
Consider a point object O placed in front of a spherical surface separating two mediums. The incident rays OD and OP meet at point I after refraction. The line NC represent a normal at the point of incidence D. Here C be the center of curvature of the surface.
From the figure
i=\alpha +\beta …(i) (being exterior angle of \displaystyle \Delta OCD)
Also
\beta =r+\gamma (being exterior angle of \displaystyle \Delta CDI)
or r=\beta -\gamma …(ii)
Also by Snell’s law
\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}=\frac{{\sin i}}{{\sin r}}=\frac{i}{r} (if i & r are small)
hence from (i) and (ii)
\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}=\frac{{\alpha +\beta }}{{\beta -\gamma }},
By cross-multiplication,
{{\mu }_{1}}(\alpha +\beta )={{\mu }_{2}}(\beta -\gamma )
\Rightarrow {{\mu }_{1}}\alpha +{{\mu }_{1}}\beta ={{\mu }_{2}}\beta -{{\mu }_{2}}\gamma
\Rightarrow {{\mu }_{1}}\alpha +{{\mu }_{2}}\gamma =({{\mu }_{2}}-{{\mu }_{1}})\beta
because if \displaystyle \alpha ,\beta ,\gamma are very small then \tan \alpha =\alpha ,\tan \beta =\beta ,\tan \gamma =\gamma hence we can write the above equation as
{{\mu }_{1}}\tan \alpha +{{\mu }_{2}}\tan \gamma =({{\mu }_{2}}-{{\mu }_{1}})\tan \beta
{{\mu }_{1}}\frac{h}{{\mathbf{QO}}}+{{\mu }_{2}}\frac{h}{{\mathbf{QI}}}=({{\mu }_{2}}-{{\mu }_{1}})\frac{h}{{\mathbf{QC}}}
If \displaystyle \alpha is small i.e., rays are paraxial & R is large, then PQ is a negligible distance hence point Q will be very close to point P therefor we can replace point Q by P so we get
{{\mu }_{1}}\frac{1}{{\mathbf{PO}}}+{{\mu }_{2}}\frac{1}{{\mathbf{PI}}}=({{\mu }_{2}}-{{\mu }_{1}})\frac{1}{{\mathbf{PC}}}
Now from the figure put OP = -u , PI = v and PC = R to get the final formula
\frac{{{{\mu }_{1}}}}{{-u}}+\frac{{{{\mu }_{2}}}}{v}=\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{R}
or \displaystyle {\frac{{{{\mu }_{2}}}}{v}-\frac{{{{\mu }_{1}}}}{u}=\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{R}}
Note:
If first medium is air, then \displaystyle {{\mu }_{1}} becomes 1, hence the formula becomes \frac{\mu }{v}-\frac{1}{u}=\frac{{\mu -1}}{R}.
Important points:
(i)
These equations are valid for all refracting surfaces convex, concave or plane. In case of plane refracting surface the radius R can be taken as \infty .
(ii)
The rules for signs for a single refracting surface are same as for spherical mirrors.
Illustration
A ray of light is incident at an angle of \displaystyle {{60}^{o}} on one face of a rectangular glass slab of thickness 0.1 m and refractive index 1.5. Calculate the lateral shift produced.
Solution
Here i = \displaystyle {{60}^{o}}; \displaystyle \mu = 1.5 and t = 0.1 m
Now, \displaystyle \mu = \frac{{\sin \,i}}{{\sin \,\,r}}
or sin r = \frac{{\sin \,i}}{\mu }\,=\,\,\frac{{\sin \,\,60{}^\circ }}{{1.5}} = \frac{{.866}}{{1.5}} = .5773
or r = \displaystyle {{35}^{o}}{{6}^{\prime}}
Now, lateral shift
d = \frac{t}{{\cos \,r}}\,\,\sin \,\,(i\,-\,r)
= \frac{{0.1}}{{\cos \,35{}^\circ {{6}^{\prime}} }} sin ( \displaystyle {{60}^{o}}-{{35}^{o}}{{6}^{\prime}})
= 0.0512 m
Illustration
A person looking through the telescope just sees a point on the rim at the bottom of a cylindrical vessel when the vessel is empty. When the vessel is completely filled with a liquid of refractive index 1.5, he observes a mark at the centre B of the bottom, without moving the telescope or the vessel. What is the height of the vessel, if the diameter of its cross-section is 10cm?
Solution
Consider a ray from B along the normal and the other as shown in figure. Let h be the height of the vessel. Then
\sin \theta =\frac{5}{{\sqrt{{{{h}^{2}}+{{5}^{2}}}}}}
and \sin {{\theta}^{\prime}} =\frac{5}{{\sqrt{{\frac{{{{h}^{2}}}}{4}+{{5}^{2}}}}}}
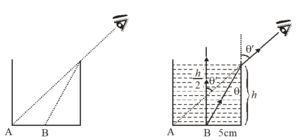
By applying the general refraction formula
({{\mu }_{1}}\sin {{\theta }_{1}}={{\mu }_{2}}\sin {{\theta }_{2}})
we have 1.5\sin \theta =1.\sin{{ \theta}^{ \prime}}
or 1.5\times \frac{5}{{\sqrt{{{{h}^{2}}+{{5}^{2}}}}}}=\frac{5}{{\sqrt{{\frac{{{{h}^{2}}}}{4}+{{5}^{2}}}}}}
or 1.5\sqrt{{\frac{{{{h}^{2}}}}{4}+25}}=\sqrt{{{{h}^{2}}+25}}
or h = 8.45 cm.
Illustration
A fish rising vertically to the surface of water in a lake uniformly at the rate of 3 m/s observes a king fisher bird diving vertically towards water at the rate 9 m/s vertically above it. If the refractive index of water is 4/3, find the actual velocity of the dive of the bird.
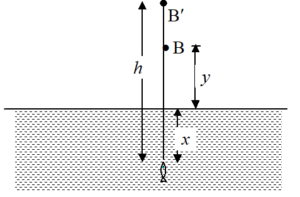
Solution
If at any instant, the fish is at a depth x below water surface while the bird at a height y above the surface, then the apparent height of the bird from the surface as seen by the fish will be given by
\displaystyle \mu = \frac{{\text{Apparent}\,\,\text{height}}}{{\text{Real}\,\,\text{height}}}
or Apparent height = \displaystyle \mu y
So the total apparent distance of the bird as seen by the fish in water will be
h = x + \displaystyle \mu y
or \frac{{dh}}{{dt}}\,=\,\frac{{dx}}{{dt}} + \displaystyle \mu \frac{{dy}}{{dt}}
or 9 = 3 + \mu \,\left( {\frac{{dy}}{{dt}}} \right)
or \frac{{dy}}{{dt}}\,=\,\frac{6}{{(4/3)}}
= 4.5 m/s
Illustration
A ray of light from a denser medium strikes a rarer medium at an angle of incidence i. If the reflected and the refracted rays are mutually perpendicular to each other, what is the value of the critical angle?
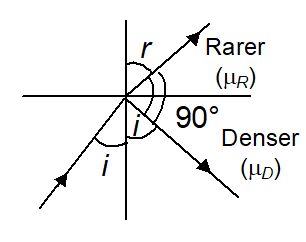
Solution
From Snell’s law, we have
\frac{{\sin \,i}}{{\sin \,r}}\,\,=\,\frac{{{{\mu }_{R}}}}{{{{\mu }_{D}}}}
or \displaystyle \mu = \frac{{{{\mu }_{D}}}}{{{{\mu }_{R}}}}\,=\,\frac{{\sin \,r}}{{\sin \,\,i}} … (i)
According to the given problem.
\displaystyle i+r+{{90}^{o}}={{180}^{o}}
or \displaystyle r={{90}^{o}}-i
Substituting the above value of r in equation (i), we get
\displaystyle \mu = \frac{{\sin \,\,(90-i)}}{{\sin \,\,i}}
or \displaystyle \mu = cot i … (ii)
By definition
C = sin–1 \left( {\frac{1}{\mu }} \right)
or C = \displaystyle {{\sin }^{{-1}}} \left( {\frac{1}{{\cot \,i}}} \right) (using equation (ii)
or C = \displaystyle {{\sin }^{{-1}}} (tan i )
Illustration
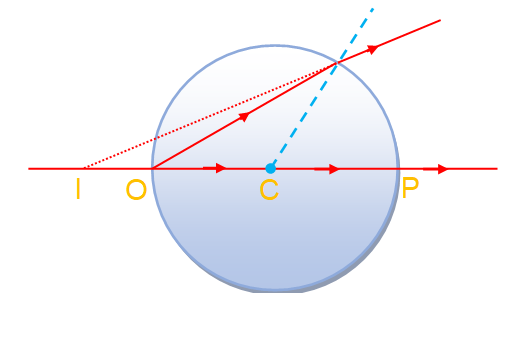
If a mark of size 0.2 cm on the surface of a glass sphere of diameter 10 cm and \displaystyle \mu = 1.5 is viewed through the diametrically opposite point, where will the image be seen and of what size?
Solution
As the mark is on one surface, refraction will take place on the other surface (which is curved). Further refraction is taking place from glass to air. So,
\displaystyle {{\mu }_{1}} = 1.5
\displaystyle {{\mu }_{2}}= 1
R = – 5 cm, u = – 10 cm, v = ?
Using the formula
\frac{{{{\mu }_{2}}}}{v}\,-\,\frac{{{{\mu }_{1}}}}{u}\,=\,\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{R},
we have
\frac{1}{v}\,-\,\frac{{1.5}}{{(-10)}}\,=\,\frac{{1-1.5}}{{-5}}
or, v = – 20 cm
Hence, the image is at a distance of 20 cm from P towards O.
In case of refraction at a curved surface, we have
m = \frac{I}{O}\,=\,\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}\,\,\frac{v}{u}\,=\,\frac{{(1.5)\,\times \,\,(-20)}}{{1\,\times \,(-10)}}\,=\,+\,3
So, the image is virtual, erect and of size I = m × O = 3 × 0.2 = 0.6 cm
Illustration
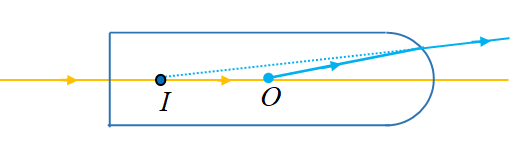
A transparent rod 40 cm long is cut flat at one end and rounded to a hemispherical surface 12 cm radius at the other end. A small object is embedded within the rod along its axis and half way between its ends. When viewed from the flat end of the rod, the object appears 12.5 cm deep. What is its apparent depth when viewed from the curved end?
Solution
Case I:
When the object is viewed from the flat surface:
Real depth of the object = 20 cm
Apparent depth = 12.5 cm
Using, \displaystyle \mu = \frac{{\text{Real}\,\,\text{depth}}}{{\text{Apparent}\,\,\text{depth}}},
we have, \displaystyle \mu = \frac{{20}}{{12.5}}\,=\,1.6
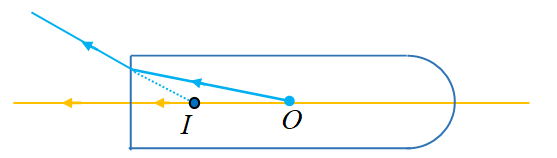
Case II:
When the object is viewed through the curved surface
Here the refraction is taking place at the single curved surface. So we will use
\frac{{{{\mu }_{2}}}}{v}\,-\,\frac{{{{\mu }_{1}}}}{u}\,=\,\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{R}
Here,
\displaystyle {{\mu }_{1}}= 1.6
\displaystyle {{\mu }_{2}} = 1
u = – 20 cm
v = ?
R = – 12 cm
So \frac{1}{v}\,-\,\frac{{1.6}}{{(-20)}}\,=\,\frac{{1-1.6}}{{-12}}
or v = – 33.3 cm
Hence the object appears 33.3 cm deep from the curved surface
Practice Questions (Basic Level)
Q.1
The principle of optical fibre is
(a) Diffraction
(b) Polarisation
(c) Interference
(d) Total Internal reflection
Ans. (d)
Q.2
A ray of light strikes a glass plate at an angle of 60° with the vertical. If the reflected and refracted rays are perpendicular to each other, the refractive index of glass is
(a) \frac{{\sqrt{3}}}{2}
(b) \frac{3}{2}
(c) \frac{1}{2}
(d) \sqrt{3}
Ans. (d)
Q.3
Light travels through a glass plate of thickness t and having refractive index m. If c be the velocity of light in vacuum, the time taken by the light to travel this thickness of glass is
(a) \frac{t}{{\mu \ c}}
(b) t m c
(c) \frac{{\mu \,t}}{c}
(d) \frac{{\mu \,t}}{c}
Ans. (c)
Q.4
The length of a vertical pole above the surface of a lake of water (n = 4/3) is 24 cm. To an under-water fish just below the water surface the tip of the pole appears to be
(a) 18 cm above the surface
(b) 24 cm above the surface
(c) 32 cm above the surface
(d) 36 cm above the surface
Ans. (c)
Q.5
A ray incident at a point at an angle of incidence of 600 enters a glass sphere of R.1. and gets reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is
(a) 500 (b) 600 (c) 900 (d) 400
Ans. (c)
Q.6
A circular beam of light of diameter d = 2 cm falls on a plane surface of glass. The angle of incidence is 600 and refractive index of glass is m = 3/2. The diameter of the refracted beam is
(a) 4.0 cm (b) 3.0 cm (c) 3.26 cm (d) 2.52 cm
Ans. (c)
Q.7
Light wave enters from medium 1 to medium 2. Its velocity in 2nd medium is double from 1st. For total internal reflection the angle of incidence must be greater than
(a) 30° (b) 60° (c) 45° (d) 90°
Ans. (a)
Q.8
The refractive index of water is 4/3 and that of glass is 5/3. Then the critical angle for a ray of light entering in water from glass will be
(a) {{\sin }^{{-1}}}\left( {\frac{4}{5}} \right)
(b) {{\sin }^{{-1}}}\left( {\frac{5}{4}} \right)
(c) {{\sin }^{{-1}}}\left( {\frac{{20}}{9}} \right)
(d) {{\sin }^{{-1}}}\left( {\frac{9}{{20}}} \right)
Ans. (a)
Q.9
A plano-convex lens has a thickness of 4 cm. When placed on a horizontal table with curved surface in contact with it, the apparent depth of the bottom most point of the lens is found to be 3 cm. If the lens is inverted such that the plane face is in contact with the table, the apparent depth of the centre of plane face is found to be 25/8 cm. The focal length of the lens is
(a) 50 cm (b) 75 cm (c) 100 cm (d) 150 cm
Ans. (b)
Q.10
A light ray falls on a square slab at an angle 45°. What must be the minimum index of refraction of glass, if total internal reflection takes place at the vertical face?
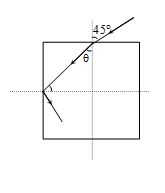
(a) \frac{{\sqrt{3}}}{2}
(b) \sqrt{{\frac{3}{2}}}
(c) \frac{3}{2}
(d) \frac{3}{{\sqrt{2}}}
Ans. (b)
Q.11
A spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O, and PO =OQ. The distance PO is equal to
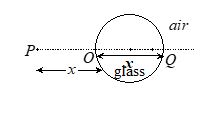
(a) 5R (b) 3R (c) 2R (d) 1.5R
Ans. (a)
Q.12
A ray of light passes through four transparent media with refractive indices m1, m2, m3 and m4 as shown in the figure. The surface of all media are parallel. If the emergent ray CD is parallel to the incident ray AB, then
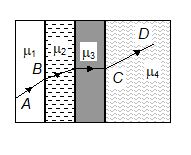
(a) m1 = m2 (b) m2 = m3 (c) m3 = m4 (d) m4 = m1
Ans. (d)
Practice Questions (JEE Main Level)
Q.1
A plane mirror is placed at the bottom of a tank containing a liquid of refractive index . P is a small object at a height h above the mirror. An observer O, vertically above P, outside the liquid, observes P and its image in the mirror. The apparent distance between these two will be
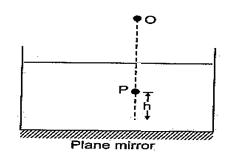
(a) \displaystyle 2\mu h
(b) \displaystyle \frac{{2h}}{\mu }
(c) \displaystyle \frac{{2h}}{{\mu -1}}
(d) \displaystyle h\left( {1+\frac{1}{\mu }} \right)
Ans (b)
Q.2
One side of a glass slab is silvered as shown. A ray of light is incident on the other side at angle of incidence \displaystyle i=45{}^\text{o}. Refractive index of glass is given as 1.5. The deviation of the ray of light from its initial path when it comes out of the slab is
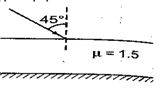
(a) 90º
(b) 180º
(c) 120º
(d) 45º
Ans (a)
Q.3
Consider the situation shown in figure. Water \displaystyle \left( {{{\mu }_{w}}=\frac{4}{3}} \right) is filled in a beaker upto a height of 10cm. A plane mirror is fixed at a height of 5 cm from the surface of water. Distance of image from the mirror after reflection from it of an object O at the bottom of the beaker is
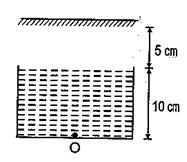
(a) 15 cm
(b) 12.5 cm
(c) 7.5 cm
(d) 10 cm
Ans (b)
Q.4
In the figure shown, \displaystyle {{\mu }_{1}}>{{\mu }_{2}}>{{\mu }_{3}}. What are the limits of angle i so that it is neither get total internal reflection at AB nor at CD ?
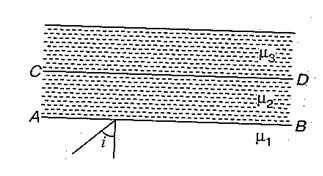
(a) \displaystyle \sin \,i\,<\,\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}
(b) \displaystyle \sin \,i\,<\,\frac{{{{\mu }_{3}}}}{{{{\mu }_{1}}}}
(c) \displaystyle \sin \,i\,<\,\frac{{{{\mu }_{3}}}}{{{{\mu }_{2}}}}
(d) None of these
Ans (b)
Q.5
A point object O is placed slightly above the centre C of a glass sphere as shown in figure. If it is viewed almost normally from above the sphere, its image is seen
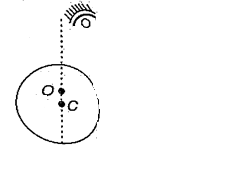
(a) at C
(b) above C
(c) below C
(d) may be above of below C
Ans (b)
Q.6
How much water should be filled in a container 21 cm in height so that it appears half filled when viewed from the top of the container?
(a) 8.0 cm (b) 10.5 cm (c) 12.0 cm (d) 14 cm
Ans. (d)
Q.7
If imj represents the refractive index when a ray of light goes from medium i to medium j, then the product 2m1 ´ 3m2 ´ 4m3 is equal to
(a) 3m1 (b) 3m2 (c) 1/1m4 (d) 1/4m2
Ans. (c)
Q.8
A ray of light from a denser medium strikes a rare medium at angle of incidence i. The reflected and the refracted rays make an angle of 90° with each other. The angles of reflection and refraction are r and r¢ respectively. The critical angle is
(a) sin–1 (tan r)
(b) sin–1 (cot i)
(c) sin–1 (tan r¢)
(d) sin–1 (sin i)
Ans. (a)
Q.9
A ray of light passes from vacuum into a medium of refractive index m. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
(a) cos–1 (m/2)
(b) sin–1 (m/2)
(c) 2 cos–1 (m/2)
(d) 2 sin–1 (m/2)
Ans. (c)
Q.10
The critical angle of light going from medium A into medium B is q. The speed of light in medium A is v. The speed of light in medium B is
(a) \frac{v}{{\sin \theta }}
(b) v sin q
(c) \frac{v}{{\tan \theta }}
(d) v tan q
Ans. (a)
Q.11
A bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is and that of the bird as estimated by the fish is , then the reactive index of liquid is
(a) \displaystyle \frac{{{{h}_{2}}}}{{{{h}_{1}}}}
(b) \displaystyle \frac{{{{h}_{1}}}}{{{{h}_{2}}}}
(c) \displaystyle \frac{{{{h}_{1}}+{{h}_{2}}}}{{{{h}_{1}}-{{h}_{2}}}}
(d) \displaystyle \frac{{{{h}_{1}}-{{h}_{2}}}}{{{{h}_{1}}+{{h}_{2}}}}
Ans. (a)
Q.12
A ray incident at an angle of incidence 60º enters a glass sphere of \displaystyle \mu =\sqrt{3}and it is reflected and refracted at the farther surface of the sphere. The angle between reflected and refracted rays at this surface is
(a) 120º (b) 90º (c) 60º (d) 150º
Ans. (b)
Q.13
Critical angle of glass is \displaystyle {{\theta }_{1}} and that of water is \displaystyle {{\theta }_{2}}. The critical angle for water and glass surface would be ( \displaystyle {{\mu }_{g}}=3/2,\,\,{{\mu }_{w}}=4/3)
(a) less than \displaystyle {{\theta }_{2}}
(b) between \displaystyle {{\theta }_{1}} and \displaystyle {{\theta }_{2}}
(c) greater than \displaystyle {{\theta }_{2}}
(d) less than \displaystyle {{\theta }_{1}}
Ans. (c)
Q.14
A 2 cm diameter coin rests flat on the bottom of a bowl in which the water is 20cm deep
( \displaystyle {{\mu }_{w}}=4/3). If the coin is viewed directly from above, what is its apparent diameter?
(a) 2 cm (b) 1.5 cm (c) 2.67 cm (d) 1.67 cm
Ans. (a)
15.
AB and CD are two slabs. The medium between the slabs has refractive index 2. Find the minimum angle of incidence at Q so that the ray is totally reflected by both the slabs.
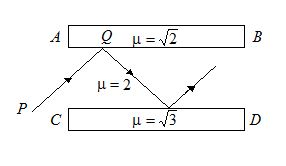
(a) 50o
(b) 90o
(c) 60o
(d) 30o
Ans (C)
16.
Figure shows a ray of light incident at an angle i on a glass slab of thickness t and refractive index m. Show that the lateral displacement, d, is given by
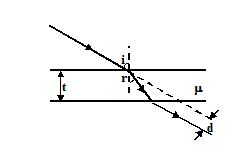
(a)t sin i \left( {1-\frac{{\cos i}}{{\sqrt{{{{\mu }^{2}}-{{{\sin }}^{3}}i}}}}} \left)
(b)t sin i \left( {1-\frac{{\sini}}{{\sqrt{{{{\mu }^{2}}-{{{\sin }}^{2}}i}}}}} \right)
(c)t sin i \left( {1-\frac{{\cos i}}{{\sqrt{{{{\mu }^{2}}-{{{\sin }}^{2}}i}}}}} \right)
(d)t sin i \left( {1-\frac{{\cos i}}{{\sqrt{{{{\mu }^{3}}-{{{\sin }}^{3}}i}}}}} \right)
Ans (c)
17.
A ray traveling in vacuum enters a long fiber of refractive index 1.5. At the curved surface the ray undergoes total internal reflection
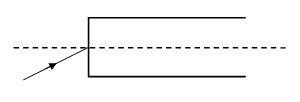
(a) for any angle of incidence.
(b) for angle of incidence between 15o and 45o
(c) for any angle of incidence between 0o and 30o
(d) for angle of incidence equal to 20o
Ans : (a)
18.
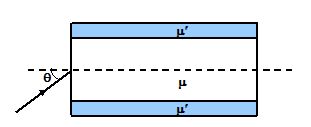
A glass cylinder of index m is surrounded by a sheath of index m¢. The surrounding medium has index m0. Show that the maximum angle q at which light will undergo total internal reflection is given by
(a) \sqrt{{{{\mu }^{2}}-\mu {{‘}^{2}}}}
(b) \sqrt{{{{\mu }^{5}}-\mu {{‘}^{5}}}}
(c) \sqrt{{{{\mu }^{3}}-\mu {{‘}^{3}}}}
(d) \sqrt{{{{\mu }^{9}}-\mu {{‘}^{9}}}}
Ans (a)
19.
A hemispherical block of glass (m = 1.5) of radius 3 cm has a circular spot at its center. When viewed vertically from above, where is the image of the spot?
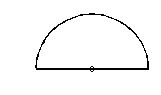
(a)at the centre
(b) in the right
(c) in the Left
(d) at the Mid
Ans (a)
Comprehension Based Question (20 and 21)
Locate the image of a small object produced by a glass sphere (n = 1.5) of radius 4 cm given that the object is located in air at
20
infinity
(a)3 cm from the centre.
(b)6 cm from the centre
(c)8 cm from the centre
(d)2 cm from the centre
Ans(b)
21.
20 cm from the centre of the sphere.
(a)8.50 cm from the centre
(b)8.57 cm from the centre
(c)8.65 cm from the centre
(d)8.00 cm from the centre
Ans(b)
Practice Questions (JEE Advance Level)
Comprehension Based Question (1 and 2)
A light ray enters into a medium whose refractive index varies along the x-axis as \mu (x)={{\mu }_{0}}\sqrt{{1+0.25x}} where m0 =1The medium is bounded by the planes x = 0,x = 1m and y = 0. If the ray enters at the origin at an angle q0 = 30° with the horizontal.
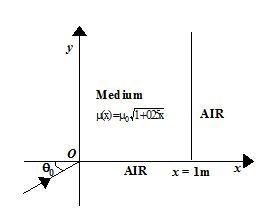
1.
Determine the trajectory of the light ray.
(a) 3 \displaystyle \left[ {\sqrt{{3+x}}-\sqrt{2}} \right]
(b) 4 \displaystyle \left[ {\sqrt{{4+x}}-\sqrt{4}} \right]
(c) 2 \displaystyle \left[ {\sqrt{{3+x}}-\sqrt{3}} \right]
(d) \displaystyle \left[ {\sqrt{{2+x}}-\sqrt{2}} \right]
Ans (c)
2.
Find the position at which it comes out of the medium.
(a)0.35m
(b) 0.54m
(c)0.40m
(d)0.20m
Ans (b)
3.
Figure shows an irregular block of material of refractive index \sqrt{2}. A ray of light strikes the face AB as shown in the figure. After refraction it is incident on a spherical surface CD of radius of curvature 0.4 m and enters a medium of refractive index 1.514 to meet PQ at E. Find the distance OEupto two places of decimal.
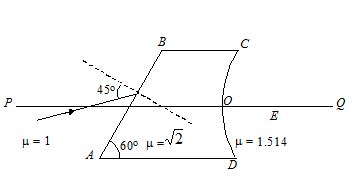
(a) 6.00 m
(b) 6.06 m
(c) 5.00 m
(d) 6.05 m
Ans (b)

