Video Lecture
Theory For Making Notes
Lens
A lens is a transparent medium bounded by two refracting surfaces such that at least one of the refracting surfaces is curved.
If the thickness of the lens is negligibly small in comparison to the object distance or the image distance, the lens is called thin. Here we shall limit our-self to thin lenses.
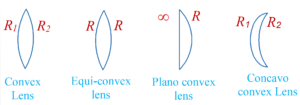
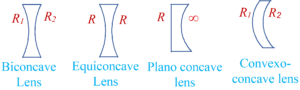
Types of lenses
Depending on the convex or concave shape of the surfaces and their radius R broadly, lenses are of the following types:
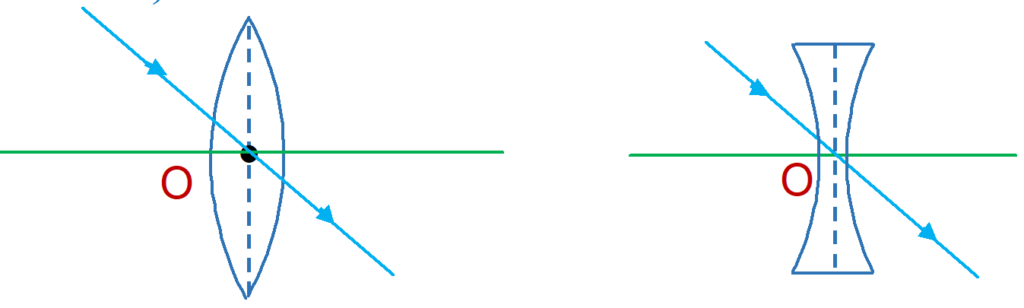
Optical centre:
Optical centre is a point for a given lens through which any ray passes undeviated
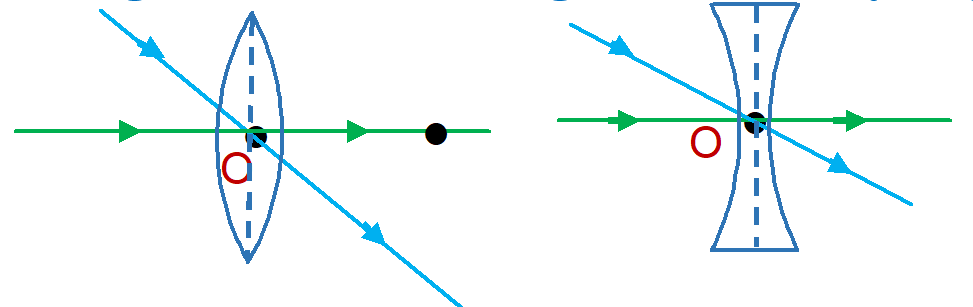
Principal axis
The line joining the centres of curvature of the two bounding surfaces is called the principal axis.
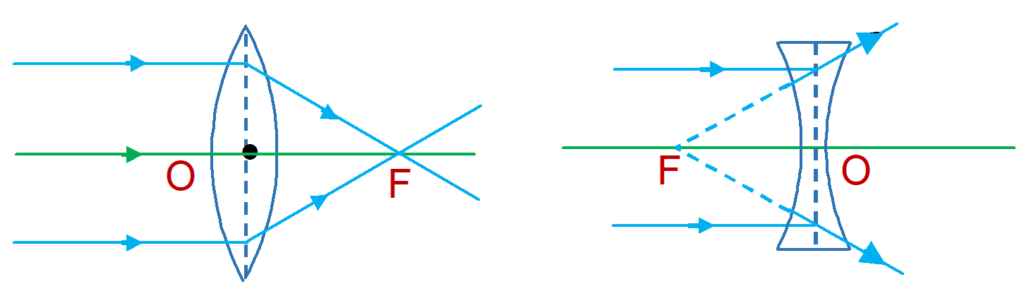
Focus (F)
A parallel beam of light, parallel and close to the principal axis of the lens after refraction passes through a fixed point on the
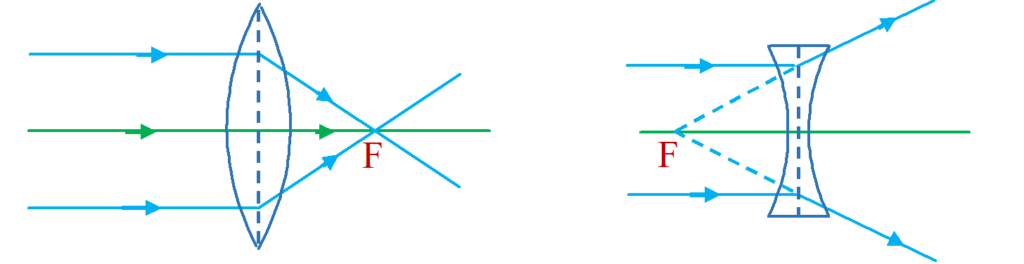
principal axis (in case of convex lens) or appear to diverge from a point on the principal axis (in case of concave lens). This point is called the principal focus or focus of the lens. It is generally denoted by F.
Lenses have two foci because light can strike the lens from both the sides.
Focal length (f)
The distance between the optical centre and the focus of a lens is called its focal length. It is denoted by f.
Sign convention
(i) Whenever and wherever possible, rays of light are taken to travel from left to right.
(ii) Distances are measured along the principal axis from the optical centre of the lens.
(iii) Distances measured along the principal axis in the direction of the incident rays are taken as positive while those measured against the direction of the incident rays are taken negative.
(iv) Distances measured above the principal axis are taken as positive and those measured below the principal axis are taken as negative.
Example:

Rules for image formation
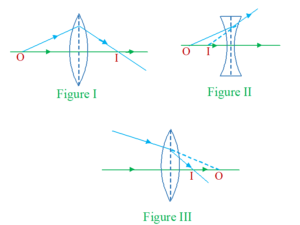
(i) A ray passing through the optical centre of the lens proceeds undeviated through the lens. (By the definition of optical centre)
(ii) A ray passing parallel to the principal axis after refraction through the lens passes or appear to pass through the focus. (By the definition of the focus)
(iii) A ray through the focus or directed towards the focus, after refraction from the lens, becomes parallel to the principal axis. (Principle of reversibility of light)
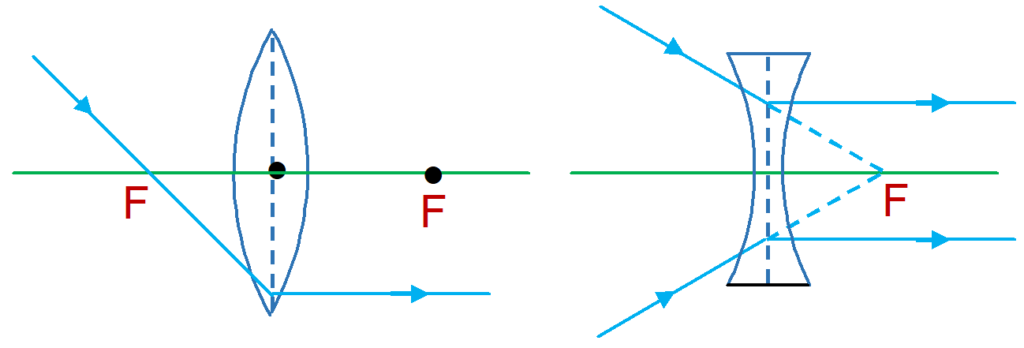
Image formation by a convex lens of the linear object
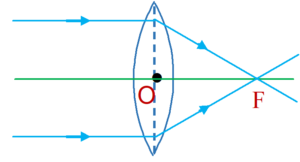
(i) When the object is at infinity:
The image is formed at F. It is real, inverted and highly diminished.
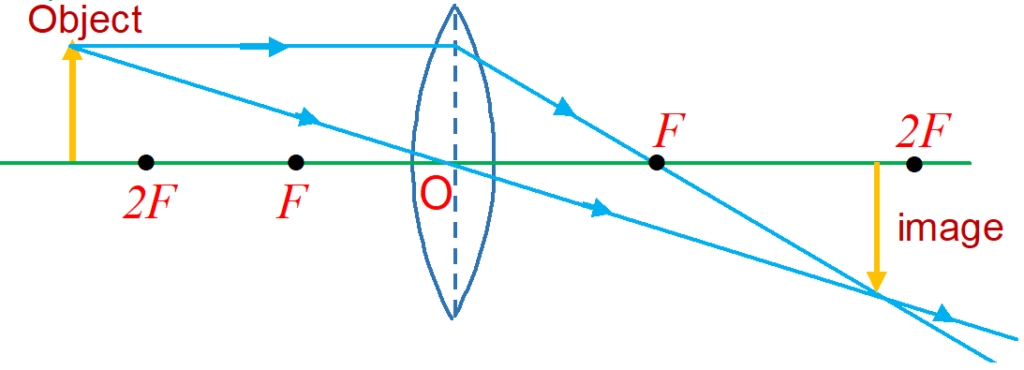
(ii) When the object is beyond 2 F:
The image is formed between F and 2F. It is real, inverted and diminished.
(iii) When the object is at 2F:
The image is formed at 2F. It is real, inverted and of the same size.
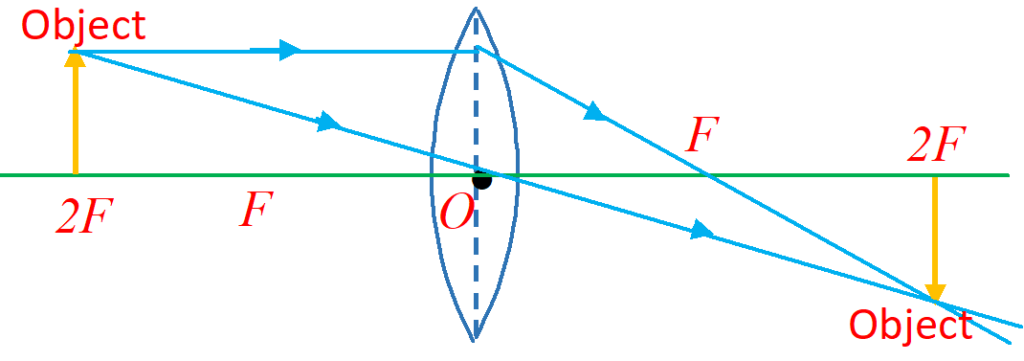
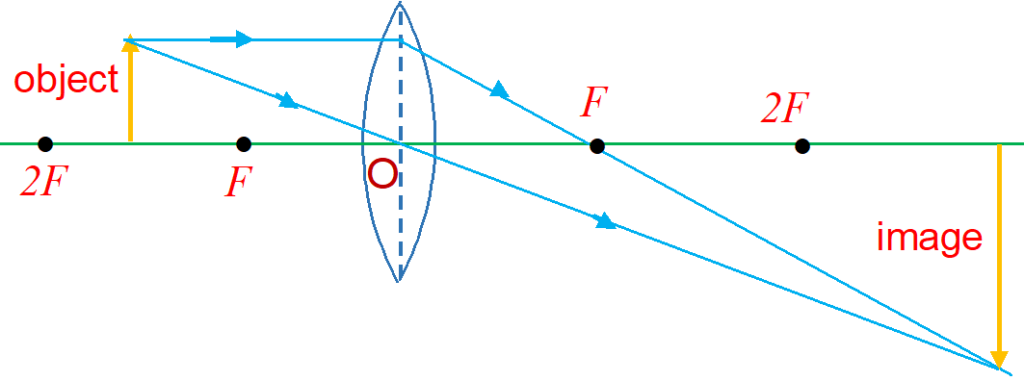
(iv) When the object is between F and 2F :
The image is formed beyond 2F (i.e., between 2F and [katex} \infty [/katex}). It is real, inverted and enlarged.
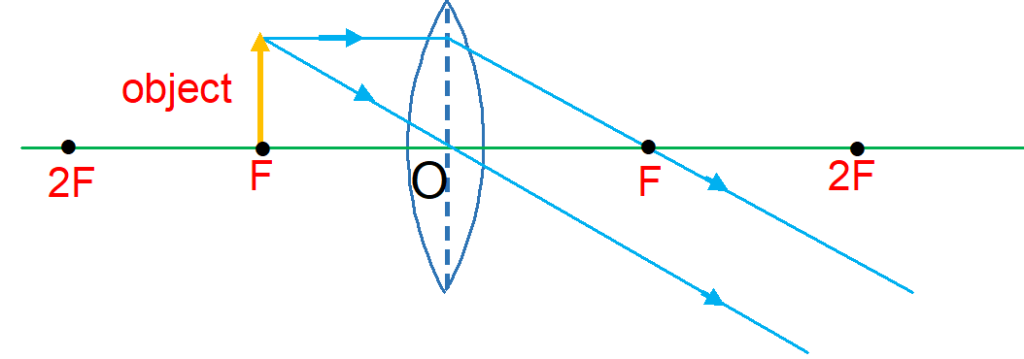
(v) When the object is at F:
The image is formed at infinity. It is real, inverted and highly diminished.
(vi) When the object is between F and O:
The image is on the same side as the object is. It is virtual, erect and magnified.
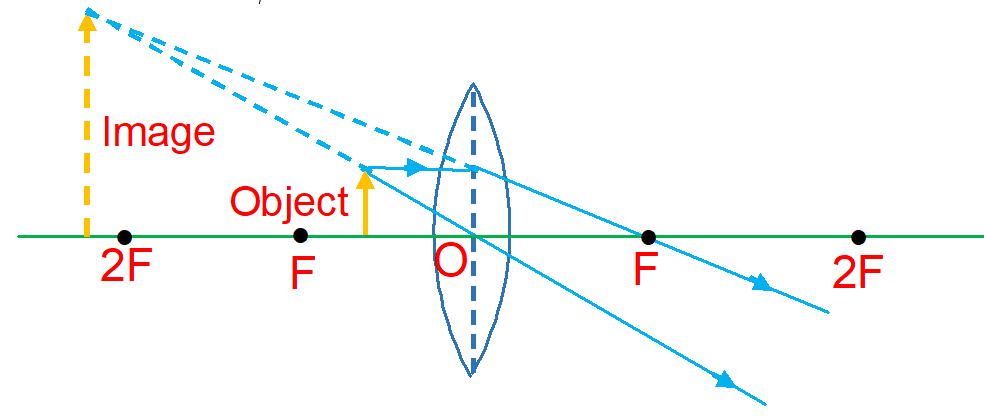
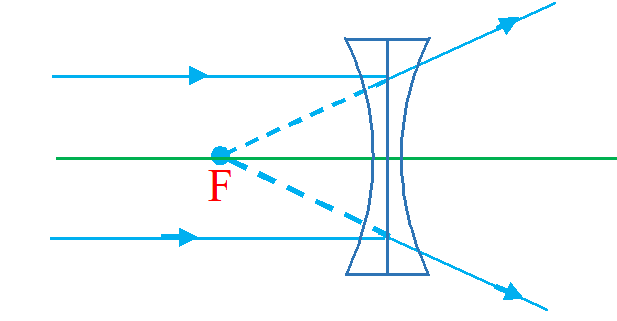
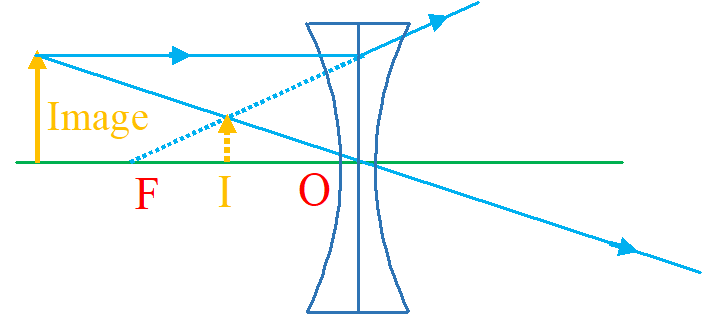
Image formation by a concave
(i) When the object is at infinity:
The image is formed at the focus. It is virtual, erect and highly diminished.
(ii) When the object is infront of the lens:
The image is formed between F and the optical centre. It is virtual, erect and diminished.
Lens formula
For a convex lens
Consider a case when an object AB is place in front of a lens. Let the real image is formed as A’B’.
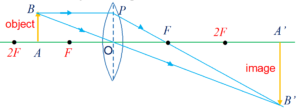
From the figure it is clear that \displaystyle \Delta ABO & \displaystyle \Delta A’B’O are similar,
\frac{{AB}}{{A\prime B\prime }}=\frac{{OB}}{{OB\prime }} ( But AB= OP from the figure)
\Rightarrow \frac{{OP}}{{A\prime B\prime }}=\frac{{OB}}{{OB\prime }} …(i)
and \displaystyle \Delta OPF & \displaystyle \Delta FA’ B’ are similar,
therefore \frac{{\mathbf{OP}}}{{\mathbf{A}\prime \mathbf{B}\prime }}=\frac{{\mathbf{OF}}}{{\mathbf{FB}\prime }} …(ii)
Comparing (i) and (iii), we get
From equation (i) and (ii)
\frac{{\mathbf{OB}}}{{\mathbf{OB}\prime }}=\frac{{\mathbf{OF}}}{{\mathbf{FB}\prime }}
Now lets put
OB = -u ,
OB’ = v ,
and OF = f
so we get
\frac{{-u}}{v}=\frac{f}{{v-f}}
\Rightarrow \text{ }-uv+uf=vf
Dividing each term by uvf, we get
-\frac{1}{f}+\frac{1}{v}=\frac{1}{u}
or \ {\frac{1}{f}=\frac{1}{v}-\frac{1}{u}}
This is called lens formula for a thin lens.
Lens formula
For a concave lens
Consider a case when an object AB is place in front of a lens. Let the virtual image is formed as A’B’.
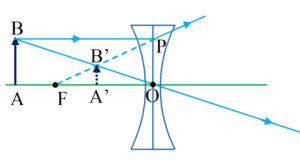
\displaystyle \Delta ABO & \displaystyle \Delta A’B’O are similar,
therefore \frac{{\mathbf{AB}}}{{\mathbf{A}\prime \mathbf{B}\prime }}=\frac{{\mathbf{OP}}}{{\mathbf{A}\prime \mathbf{B}\prime }}=\frac{{\mathbf{BO}}}{{\mathbf{B}\prime \mathbf{O}}} …(1)
\displaystyle \Delta OPF & \displaystyle \Delta B’A’F are similar,
therefore \frac{{\mathbf{OP}}}{{\mathbf{A}\prime \mathbf{B}\prime }}=\frac{{\mathbf{OF}}}{{\mathbf{FB}\prime }} …(2)
Comparing (1) and (2), we get \frac{{\mathbf{OB}}}{{\mathbf{OB}\prime }}=\frac{{\mathbf{OF}}}{{\mathbf{FB}\prime }}
Using sign convention, we get
\frac{{-u}}{{-v}}=\frac{{-f}}{{(-f)-(-v)}}
or \frac{u}{v}=\frac{f}{{f-v}}
or uf – uv = vf
or uv = uf – vf
Dividing each term by uvf, we get
\frac{1}{f}=\frac{1}{v}-\frac{1}{u}
So the lens formula is same for all types of lenses.
Linear magnification (m)
For a convex lens:
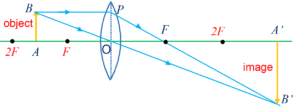
\displaystyle \Delta ABO & \displaystyle \Delta A’B’O are similar,
therefore \frac{{\mathbf{A}\prime \mathbf{B}\prime }}{{\mathbf{AB}}}=\frac{{\mathbf{B}\prime \mathbf{O}}}{{\mathbf{BO}}}
Using sign convention, we get
\frac{{-\mathbf{I}}}{\mathbf{O}}=\frac{v}{{-u}}
therefore
m=\frac{\mathbf{I}}{\mathbf{O}}=\frac{v}{u}
Note: There is no minus sign before (v/u) as was in case of a convex mirror.
For a concave lens:
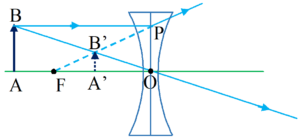
ABO & \displaystyle \Delta A’B’O are similar,
therefore \frac{{\mathbf{A}\prime \mathbf{B}\prime }}{{\mathbf{AB}}}=\frac{{\mathbf{OB}\prime }}{{\mathbf{OB}}}
using sign convention, we get
\frac{\mathbf{I}}{\mathbf{O}}=\frac{{-v}}{{-u}}
or
m=\frac{I}{O} =\frac{v}{u}
Power of a lens
The power of a lens is defined as P = \frac{1}{f} where f must be expressed in metres.
The SI unit of power of a lens is \displaystyle {{m}^{{-1}}}. It is also known as dioptre (D). The focal length of a convex lens is positive. So, the power of a convex lens is positive. The focal length of a concave lens is negative. So, the power of a concave lens is negative.
Note that the focal length of a lens depends on the medium in which it is kept. Therefore the power of a lens also depends on the medium.
Combination of lenses and mirrors
When several lenses or mirrors are used co-axially, the image formation is considered one after another in steps. The image formed by the lens facing the object serves as object for the next lens or mirror; the image formed by the second lens (or mirror) acts as object for the third and so on. The total magnification in such situations will be given by
m = \frac{I}{O}\,=\,\frac{{{{I}_{\mathbf{1}}}}}{O}\,\times \,\,\frac{{{{I}_{\mathbf{2}}}}}{{{{I}_{\mathbf{1}}}}}\,\times …
or, \displaystyle m={{m}_{1}}\times {{m}_{2}}\times {{m}_{3}}~\times \text{ }\ldots ..
Equivalent focal length (F) and power (P) of two lenses kept in contact:
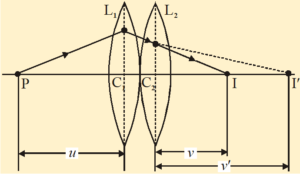
Consider a point object placed at P. Let I’ is the image formed of object O by first lens \displaystyle {{L}_{1}}. Thus I’ acts as virtual object for the second lens \displaystyle {{L}_{2}}. Let I be the image formed of this virtual object I’ by the second lens \displaystyle {{L}_{2}}.
therefore for first lens \frac{1}{{v\prime }}-\frac{1}{u}=\frac{1}{f} …(i)
and for second lens \frac{1}{v}-\frac{1}{{v\prime }}=\frac{1}{{{{f}_{2}}}} …(ii)
By adding, (i) and (ii) we get
\frac{1}{v}-\frac{1}{u}=\frac{1}{{{{f}_{1}}}}+\frac{1}{{{{f}_{2}}}}
Now, if we consider both the lens as one only whose equivalent focal length is F, then
\frac{1}{v}-\frac{1}{u}=\frac{1}{F}
Form (i) and (ii), we get
\frac{1}{F}=\frac{1}{{{{f}_{1}}}}+\frac{1}{{{{f}_{2}}}}
Accordingly, {P={{P}_{1}}+{{P}_{2}}}
Where P stands for power.
Note:
1.
For convex lenses \displaystyle {{f}_{1}}, \displaystyle {{f}_{2}}, \displaystyle {{P}_{1}}, and \displaystyle {{P}_{2}} all are (+). For concave lens they are all (–).
2.
If the two lenses of focal lengths \displaystyle {{f}_{1}} and \displaystyle {{f}_{2}}are placed coaxially separated by a distance d, the focal length f of both lenses together is given by
{\frac{1}{f}=\frac{1}{{{{f}_{1}}}}+\frac{1}{{{{f}_{2}}}}-\frac{d}{{{{f}_{1}}{{f}_{2}}}}}
or P={{P}_{1}}+{{P}_{2}}-d\,{{P}_{1}}{{P}_{2}}
Displacement method to determine the focal length of a convex lens
Let us consider a real object `O’ and a screen `S’ fixed at a distance D apart. A convex lens is placed between them.
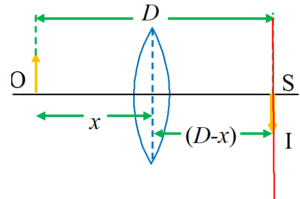
Let us consider a real object `O’ and a screen `S’ fixed at a distance D apart. A convex lens is placed between them.
Let x be the distance of the object from the lens when its real image `I’ is obtained on the screen.
So we have , u = – x
v = + (D – x)
f = + f
Using these values in the lens formula, we have
\frac{1}{{(D-x)}}\,-\frac{1}{{-x}}\,=\,\frac{1}{f}
or, \frac{1}{{(D-x)}}\,+\,\frac{1}{x}\,=\,\frac{1}{f}
or, \frac{D}{{(D-x)\,x}}\,=\,\frac{1}{f}
or, \displaystyle {{x}^{2}} – Dx + Df = 0
or, x = \frac{{D\,\pm \,\sqrt{{{{D}^{2}}-4Df}}}}{2}\,=\,\frac{{D\,\pm \,\sqrt{{D(D-4f)}}}}{2}
Now, there are three possibilities.
(i) If D < 4f
then in this case, x will be imaginary and so physically no position of lens is possible.
(ii) If D = 4 f
then in this case, x = \frac{D}{2}=\,2f. So only one position of the lens will be possible and in this situation.
v = D – x = 4f – 2f = 2f ( = x)
(iii) If D > 4f
in this situation both the roots of x will be real.
Thus \displaystyle {{x}_{1}} = \frac{{D\,-\,\sqrt{{D(D-4f)}}}}{2}
and \displaystyle {{x}_{2}} = \frac{{D+\sqrt{{D\,(D-\,4f)}}}}{2}
So if D > 4f, these are two positions of lens at distances \displaystyle {{x}_{1}} and \displaystyle {{x}_{2}} from the object for which real image is obtained on the screen. This method is called ‘Displacement method’ and is used in laboratory to determine the focal length of the convex lens.

In case of displacement method, if the distance between two positions of the lens is L, then
L = \displaystyle {{x}_{2}}-{{x}_{1}} = \sqrt{{D\,(D\,-\,4\,f)}}
or \displaystyle {{L}^{2}}={{D}^{2}}4Df
Þ f = \frac{{{{D}^{2}}-{{L}^{2}}}}{{4\,D}}
We have
L = ( \displaystyle {{x}_{2}}-{{x}_{1}})
and D = \displaystyle {{x}_{2}}+{{x}_{1}}
therefore
\displaystyle {{x}_{1}} = \frac{{D-L}}{2}\,;\,\,{{x}_{2}}\,=\,\,\frac{{D+L}}{2}\,
Now, \displaystyle {{x}_{2}}+{{x}_{1}} = \frac{{D-L}}{2}\,+\,\frac{{D+L}}{2}\,=\,D
\Rightarrow \displaystyle {{x}_{1}}=D{{x}_{2}} & \displaystyle {{x}_{2}}=D{{x}_{1}}
Hence object and image distances are interchanged in the two positions of the lens. Let the magnification be \displaystyle {{m}_{1}} and \displaystyle {{m}_{2}}.
therefore
\displaystyle {{m}_{1}} = \frac{{(D\,-\,{{x}_{1}})}}{{-{{x}_{1}}}}\,=\,\frac{{{{x}_{2}}}}{{{{x}_{1}}}}
and
\displaystyle {{m}_{2}} = \frac{{(D-{{x}_{2}})}}{{-{{x}_{2}}}}\,=\,-\,\frac{{{{x}_{1}}}}{{{{x}_{2}}}}
Now, \displaystyle {{m}_{1}}\times {{m}_{2}} = \frac{{{{x}_{2}}}}{{-{{x}_{1}}}}\,\times \,\frac{{-{{x}_{1}}}}{{{{x}_{2}}}}= 1
or \frac{{{{\mathbf{I}}_{\mathbf{1}}}}}{\mathbf{O}}\,\,\frac{{{{\mathbf{I}}_{\mathbf{2}}}}}{\mathbf{O}}\,\,=\,\,\mathbf{1}
Þ O = object size = \sqrt{{{{I}_{1}}{{I}_{2}}}}
i.e., the size of the object is the geometric mean of the sizes of the two images.
Illustration
A magnifying lens has a focal length of 10 cm. (i) Where should the object be placed if the image is to be 30 cm from the lens? (ii) What will be the magnification?
Solution
(i)
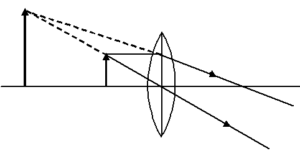
In case of magnifying lens, the lens is convergent and the image is erect, virtual and enlarged and between infinity and the object on the same side of the lens as shown in the above diagram.
So, here f = + 10 cm; v = – 30 cm
Let x be the object distance
Using lens formula \frac{1}{f}\,=\,\frac{1}{v}\,-\,\frac{1}{u}\,,
we have, \frac{1}{{-30}}\,-\,\frac{1}{{((-x)}}\,=\,\frac{1}{{10}}
Þ x = 7.5 cm
(ii) m = \frac{\mathbf{I}}{\mathbf{O}}\,=\,\frac{v}{u}\,=\,\frac{{-30}}{{-8.5}} = + 4
Thus, the image is erect and virtual and four times of the object.
Illustration
An object 25 cm high is placed in front of a convex lens of focal length 30 cm. If the height of the image formed is 50 cm, find the distance between the object and the image?
Solution
We have
\displaystyle \left| m \right| = \frac{\mathbf{I}}{\mathbf{O}}\,=\,\frac{v}{u}\,=\,\frac{{50}}{{25}}\,=\,2
There are two possibilities
(i)
If the image is inverted (i.e., real)
m = \frac{v}{u}\,=\,-\,2
or v = – 2u
Let x be the object distance in this case
We have
u = – x ,
v = + 2 x ,
f = + 30 cm
Using lens formula, we have
\frac{1}{{2x}}\,-\,\frac{1}{{-x}} = \frac{1}{{30}}
or x = 45 cm
Hence, the distance between the object and the image = 45 + 90 = 135 cm.
(ii)
If the image is erect (i.e., virtual)
m = \frac{v}{u}\,=\,+\,2
Let x’ be the object distance
we have u = – x ¢ ,
v = – 2 x¢ ,
f = + 30
Using the lens formula, we have \frac{1}{{-2x\,\prime }}\,+\,\frac{1}{x}\,=\,\frac{1}{{30}}
Þ x¢ = 15 cm
Hence, the distance between the object and the image = 15 cm
Illustration
Two thin lenses, both of 10 cm focal length- one convex and other concave, are placed 5 cm apart. An object is placed 20 cm in front of the convex lens. Find the nature and position of the final image.
Solution
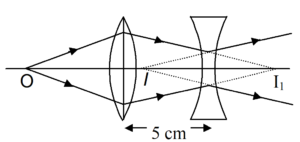
For refraction at the convex lens,
we have u = – 20 cm,
\displaystyle {{f}_{1}} = + 10 cm,
v = \displaystyle {{v}_{1}} = ?
Using lens formula,
we have \frac{1}{{{{v}_{1}}}}\,-\,\frac{1}{{(-20)}}\,=\,\,\frac{1}{{10}}
Þ \displaystyle {{v}_{1}} = 0 + 20 cm
The convex lens produces converging rays trying to meet at \displaystyle {{l}_{1}}, 20 cm from the convex lens, i.e., 15 cm behind the concave lens.
\displaystyle {{l}_{1}} will serve as a virtual object for the concave lens.
For refraction at the concave lens.
We have
u = + 15 cm,
f = – 10 cm,
v = ?
Using lens formula, we have
\frac{1}{v}\,-\,\frac{1}{{15}}\,=\,-\,\frac{1}{{10}}
Þ v = – 30 cm
Hence the final image is virtual and is located at 30 cm to the left of concave lens.
Illustration
A point object is placed at a distance of 12 cm on the axis of a convex lens of focal length 10 cm. On the other side of the lens, a convex mirror is placed at the distance of 10 cm from the lens such that the image formed by the combination coincides with the object itself. What is the focal length of the mirror?
Solution
For the refraction at the convex lens, we have
u = – 12 cm; v = ? f = + 10 cm
Using lens formula, we have
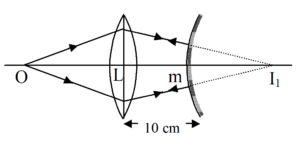
\frac{1}{v}\,-\,\frac{1}{{(-12)}}\,=\,\frac{1}{{10}}
or, v = + 60 cm
Thus, in the absence of the convex mirror, convex lens will form the image \displaystyle {{l}_{1}}, at a distance of 60 cm behind the lens. As the mirror is at a distance of 10 cm from the lens, \displaystyle {{l}_{1}} will be at a distance of (60 – 10) = 50 cm from the mirror i.e., \displaystyle M{{l}_{1}} = 50 cm.
Now, as the final image \displaystyle {{l}_{2}} is formed at the object itself, the rays after reflection from the mirror retraces its path i.e., the rays on the mirror are incident normally, i.e., \displaystyle {{l}_{1}} is the centre of the mirror so that
R = \displaystyle M{{l}_{1}} = + 50 cm
and f = \frac{R}{2}\,=\,\frac{{50}}{2}\,\,= + 25 cm
Illustration
An object is kept at a distance of 100 cm from a screen. A convex lens placed between them produces a real & magnified image on the screen. If the lens is shifted 30 cm towards the screen, real image is again obtained. Find the focal length of the lens. Also calculate the size of the object if the image sizes are 16 mm and 9 mm respectively.
Solution
Here, D = 100 cm; L = 30 cm
therefore
f = \frac{{{{D}^{2}}-{{L}^{2}}}}{{4\,D}}\,=\,\,\frac{{{{{(100)}}^{2}}-{{{(30)}}^{2}}}}{{4\,(100)}}= \frac{{91}}{4} cm
\displaystyle {{l}_{1}} = 16 mm; \displaystyle {{l}_{2}} = 9 mm
therefore Object size = \sqrt{{{{I}_{1}}\,{{I}_{2}}}}\,=\,\sqrt{{16\,\times \,9}} = 12 mm
Illustration
The distance between two point sources of light is 24 cm. Find out where you will place a converging lens of focal length 9 cm, if the images of both sources are formed at the same point.
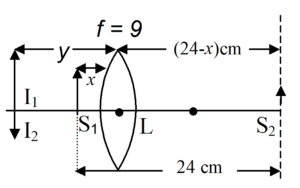
Solution
As images of both sources are coincident, the lens must be placed between the sources such that \displaystyle {{S}_{1}} forms the virtual image on same side while \displaystyle {{S}_{2}} real image on opposite side as shown in figure. Now if x cm and y cm are the distances of sources \displaystyle {{S}_{1}} and its image from lens L respectively.
\frac{1}{{-y}}\,-\,\frac{1}{{-x}}\,=\,\frac{1}{9}
Now as the distance between \displaystyle {{S}_{1}} and \displaystyle {{S}_{2}} is is 24 cm, the distance of \displaystyle {{S}_{2}} from lens L, i.e., u will be (24 – x) cm and as image of \displaystyle {{S}_{2}} is coincident with that of \displaystyle {{S}_{1}}, v = y. So for \displaystyle {{S}_{2}}
\frac{1}{y}\,-\,\frac{1}{{-(24-x)}}\,=\,\frac{1}{9}
Adding Equation (1) and (2),
\frac{1}{x}\,+\,\frac{1}{{(24-x)}}=\,\frac{2}{9}
i.e., \displaystyle {{x}^{2}}\text{ }24x+\text{ }108\text{ }=\text{ }0
so that x = \frac{1}{2}\,\left[ {24\,\pm \,\sqrt{{{{{24}}^{2}}-4\,\times \,108}}} \right] or, x = 12 ± 6 i.e., x = 6 cm or 18 cm
So the lens must be placed at a distance of 6 cm or 18 cm from one of the sources.
Illustration
An object is placed infront of a concave mirror of focal length f. A virtual image is formed with a magnification of 2. To obtain a real image of same magnification, by what distance must the object has to be moved ?
Solution
In the first case. Let x be the distance of object from the mirror. Then
u = – x
v = + 2x
f = –f
Using \displaystyle \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
Or \displaystyle \frac{1}{{2x}}-\frac{1}{x}=-\frac{1}{f}
Or \displaystyle x=\frac{f}{2}
In the second case, let y be the distance of the object from the mirror. Then
u = – y, v = – 2 y and
f = – f
So \displaystyle \frac{1}{{-2y}}-\frac{1}{y}=-\frac{1}{f}
therefore
\displaystyle y=\frac{3}{2}f
So, object will have to be moved by a distance of y – x, i.e., f.
Illustration
A plano convex glass lens (µg = 3/2) of radius of curvature R = 10 cm is placed at a distance of b from a concave lens of focal length 20 cm. What should be the distance a of a point object O from the plano convex lens so that the position of final image is independent of b
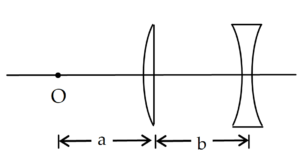
Solution
Focal length of plano convex lens is
\displaystyle \frac{1}{f}=\left( {\frac{3}{2}-1} \right)\,\,\left( {\frac{1}{{10}}-\frac{1}{\infty }} \right)
Or f = 20 cm
If point object O is placed at a distance of 20 cm from the plano convex lens ray become parallel and final image is formed at second focus or 20 cm from concave lens which is independent of b.
Illustration
In figure, length of the object AB is 9 cm. Find the nature and position of the final image and also its length. Assume that each lens is a thin lens.
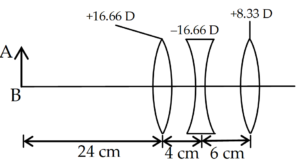
Solution
Action of first lens
Focal length \displaystyle =\frac{1}{{16.66}}=0.06\ \text{m}=6\ \text{cm}
u = – 24 cm
Using \displaystyle \frac{1}{v}-\frac{1}{u}=\frac{1}{f}
\displaystyle \frac{1}{v}+\frac{1}{{24}}=\frac{1}{6}
\displaystyle \frac{1}{v}=\frac{1}{6}-\frac{1}{{24}}
or v = 8 cm
This image would be real and inverted (with respect to object AB).
Its magnification \displaystyle {{m}_{1}}=\frac{v}{u}=\frac{8}{{-24}}=-\frac{1}{3}
Action of second lens
Image formed by first lens, being at distance 8 cm right of first lens, would act as virtual object for the second lens.
Focal length \displaystyle =\frac{1}{{-16.66}}=-0.06\ \text{m}=-6\ \text{cm}
u = + 4 cm [distance of image formed by first lens from the second lens]
\displaystyle \frac{1}{v}-\frac{1}{4}=-\frac{1}{6}
therefore \displaystyle \frac{1}{v}=\frac{1}{4}-\frac{1}{6}=\frac{1}{{12}}
therefore v = 12 cm
Thus the second lens forms an image 12 cm to its right. This image is real and its magnification,
\displaystyle {{m}_{2}}=\frac{v}{u}=\frac{{12}}{4}=3
Thus it is also erect relative to image formed by the first lens.
Action of third lens
Image formed by the second lens, being 12 cm to its right, will act as a virtual object for the third lens.
Focal length \displaystyle =\frac{1}{{8.33}}=0.12\ \text{m}=12\ \text{cm}
\displaystyle u=+6\ \text{cm} [distance of image formed by second lens from the third lens]
therefore \displaystyle \frac{1}{v}-\frac{1}{6}=\frac{1}{{12}}
or \displaystyle \frac{1}{v}=\frac{1}{{12}}+\frac{1}{6}
therefore v = 4 cm
Thus the final image forms 4 cm to the right of third lens. The image will be real and its magnification,
\displaystyle {{m}_{3}}=\frac{v}{u}=\frac{4}{6}=\frac{2}{3}
This image is erect relative to the image formed by second lens.
Total magnification \displaystyle m={{m}_{1}}\times {{m}_{2}}\times {{m}_{3}}
\displaystyle =-\frac{1}{3}\times 3\times \frac{2}{3}
therefore \displaystyle m=-\frac{2}{3}
Hence the final image is, relative to the given object, inverted and also reduced in size. It forms 4 cm right of the third lens and it is a real image.
To obtain length of the final image
\displaystyle m=\frac{I}{O}=-\frac{2}{3}
therefore \displaystyle I=-\frac{2}{3}\times 9=-6\ \text{cm}
Practice Questions (Basic Level)
Q.1
An object is placed at a distance of 3f from a convex lens of focal length f. A slab of refractive index m is placed in between lens and object. The image of the object will be formed nearest to the object if thickness of the slab is
(a) f
(b) 2f
(c) \frac{f}{{\mu -1}}
(d) \frac{{\mu f}}{{\mu -1}}
Ans. (d)
Q.2
A concave lens of focal length 10 cm and a convex lens of focal length 20 cm are placed certain distance apart. If parallel rays incident on one lens become converging after passing through other lens, then the separation between the lenses must be greater than
(a) zero (b) 5 cm (c) 10 cm (d) 9 cm
Ans. (c)
Q.3
The distance between an object and the screen is 100 cm. A lens produces an image on the screen when placed at either of the positions 40 cm apart. The power of the lens is nearly
(a) 3 dioptres (b) 5 dioptres (c) 7 dioptres (d) 9 dioptres
Ans. (b)
Q.4
If two lenses of power +5 diopters are mounted at some distance apart, the combination will always behave like a diverging lens if the distance between them is
(a) Greater than 40 cm
(b) Equal than 40 cm
(c) Equal to 10 cm
(d) Less than 10 cm
Ans. (a)
Q.5
A convex lens of focal length 12 cm is made of glass of m = \frac{3}{2}. What will be its focal length when immersed in liquid of m = \frac{5}{4}
(a) 6 cm (b) 12 cm (c) 24 cm (d) 30 cm
Ans. (d)
Q.6
A lens of power +2 diopters is placed in contact with a lens of power –1 diopter. The combination will behave like
(a) A convergent lens of focal length 50 cm
(b) A divergent lens of focal length 100 cm
(c) A convergent lens of focal length 100 cm
(d) A convergent lens of focal length 200 cm
Ans. (c)
Q.7
A concave lens of focal length F produces an image equal to 1/n of size of object, the distance of the image, from the lens is
(a) (n+1)F
(b) (n-1)F
(c) \left( {\frac{{n+1}}{n}} \right)F
(d) \left( {\frac{{n-1}}{n}} \right)F
Ans. (d)
Q.8
A convex lens A of focal length 20 cm and a concave lens B of focal length 5 cm are kept along the same axis with a distance d between them. If a parallel beam of light falling on A leaves B as a parallel beam, then the distance d in cm will be
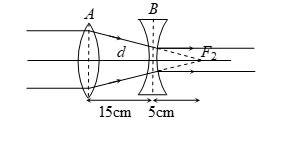
(a) 25 (b) 15 (c) 30 (d) 50
Ans. (b)
Q.9
Two convex lenses placed in contact form the image of a distant object at P. If the lens B is moved to the right, the image will
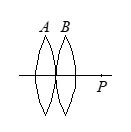
(a) move to the left
(b) move to the right
(c) remain at P
(d) move either to the left or right, depending upon focal lengths of the lenses
Ans. (b)
Practice Questions (JEE Main Level)
Q.1
A thin plano-convex glass lens (m = 1.5) has its plane surface silvered and R is the radius of curvature of curved part, then which of the following ray diagram is true for an object placed at O?
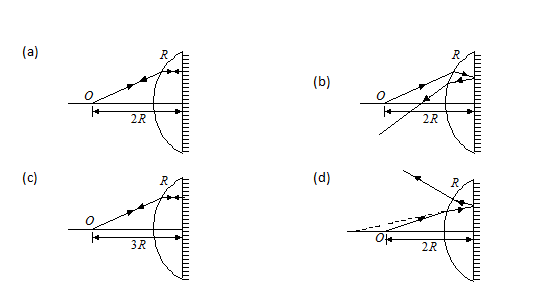
Ans (a)
Q.2
Two convex lenses placed in contact form the image of a distant object at P. If the lens B is moved to the right, the image will
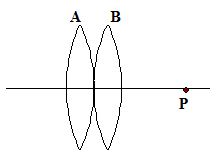
(a) move to the left
(b) move to the right
(c) remain at P
(d) move either to the left or right, depending upon focal lengths of the lenses
Ans (b)
Q.3
An object, a convex lens of focal length 20 cm and a plane mirror are arranged as shown in the figure. How far behind the mirror is the final image formed?
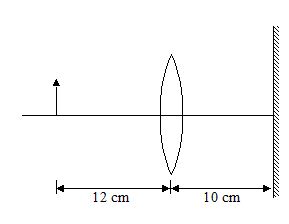
(a) 30 cm
(b) 20 cm
(c) 40 cm
(d) 50 cm
Ans (a)
Q.4
A plano convex glass lens ( \displaystyle {{\mu }_{g}}=3/2) of radius of curvature R = 10 cm is placed at a distance b from a concave lens of focal length 20 cm. What should be the distance a of a point object O from the plano convex lens so that the position of final image is always at same distance from concave lens
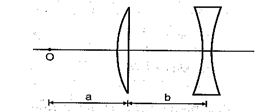
(a) 40 cm
(b) 60 cm
(c) 30 cm
(d) 20 cm
Ans (d)
Q.5
A convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object is placed at a distance of 20 cm from the lens. Then
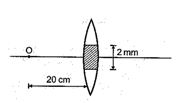
(a) only one image will be formed by the lens
(b) the distance between the two images formed by such a lens is 6 mm
(c) the distance between the images is 4 mm
(d) the distance between the images is 2 mm
Ans (a)
Q.6
A converging lens of focal length 20 cm and diameter 5 cm is cut along the line AB. The upper part of the lens shown in the diagram is now used to form an image of a point P placed 30 cm away from it on the line XY. The image of P will be formed
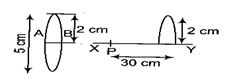
(a) 0.5 cm above XY
(b) 1 cm below XY
(c) on XY
(d) 1.5 cm below XY
Ans (d)
Q.7
A point object is kept at the first focus of a convex lens. If the lens starts moving towards right with a constant velocity, the image will
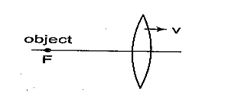
(a) always move towards right
(b) always move towards left
(c) first move towards right and then towards left
(d) first move towards left and then towards right
Ans (d)
Q.8
A convex lens of focal length 20 cm is placed co-axially with a concave lens of
focal length 5 cm. The parallel beam incident on convex lens leaves the concave lens as a parallel beam. The separation between the lenses is
(a) 20 cm (b) 15 cm (c) 25 cm (d) 10 cm
Ans. (d)
Q.9
An object is placed first at infinity and then at 20 cm from the object side focal plane of a convex lens. The two images thus formed are 5 cm apart. The focal length of the lens is
(a) 5 cm (b) 10 cm (c) 15 cm (d) 20 cm
Ans. (b)
Q.10
The minimum distance between an object and its real image formed by a convex lens of focal length f is
(a) 2f (b) 4f (c) 6f (d) none of these
Ans. (b)
Q.11
When the object is at distances u1 and u2 from the optical center of a convex lens, a real and a virtual image of the same magnification is obtained. The focal length of the lens is
(a) \frac{{{{u}_{1}}-{{u}_{2}}}}{2}
(b) 2{{u}_{1}}
(c) 2{{u}_{2}}
(d) \frac{{{{u}_{1}}+{{u}_{2}}}}{2}
Ans. (d)
Q.12
A point P is at a distance of h from the principle axis of a convex lens of focal length f lying inside the lens. The deviation of incident ray incident at the point P is independent of
(a) h
(b) f
(c) distance of object
(d) cannot be determined
Ans. (a)
Q.13
Two convex lenses of focal length 10 cm and 20 cm respectively placed coaxially and are separated by some distance d. The whole system behaves like a concave lens. One of the possible value of d is
(a) 15 cm (b) 20 cm (c) 25 cm (d) 40 cm
Ans.. (c)
Q.14
Two point sources \displaystyle {{S}_{1}} and \displaystyle {{S}_{2}} are 24 cm apart. Where should a convex lens of focal length 9 cm be placed in between them so that the images of both sources are formed at the same place ?
(a) 6 cm from \displaystyle {{S}_{1}}
(b) 15 cm from \displaystyle {{S}_{1}}
(c) 10 cm from \displaystyle {{S}_{1}}
(d) 12 cm from \displaystyle {{S}_{1}}
Ans. (a)
Q.15
A convex lens forms a real image three times larger than the object on a screen. Object and screen are moved until the image becomes twice the size of the object. If the shift of the object is 6 cm. The shift of screen is
(a) 36 cm (b) 72 cm (c) 18 cm (d) 9 cm
Ans. (a)
16.
An object of height 2 cm is 20 cm from a converging lens (f = 10cm), which is located at a distance 12 cm in front of a diverging lens (f = -15 cm). Find the location of the final image and its transverse magnification. Draw a ray diagram.
(a)17.9 cm; -2.50
(b)20.10 cm; -5.00
(c)15.5 cm;-3.00
(d)17.1 cm; -2.14
Ans (d)
Practice Questions (JEE Advance Level)
1.
A point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2 m. It then cut into two halves each of which is displaced by 0.0005 m as shown in figure. Find the position of the image. If more than one image is formed, find their number and the distance between them.
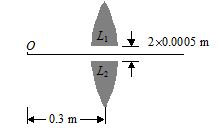
(a) 2; 0.003 m
(b) 3; 0.009 m
(c) 4; 0.008 m
(d) 5; 0.005 m
Ans (a)
2.
An object is approaching a thin convex lens of focal length 0.3 m with a speed of 0.01 m/s. Find the magnitudes of the rates of change of position and lateral magnification of image when the object is at a distance of 0.4 m from the lens.
(a)0.02 m/s, 0.4 s-1
(b)0.09 m/s, 0.3 s-1
(c)0.05 m/s, 0.5 s-1
(d)0.01 m/s, 0.8 s-1
Ans (b)
3.
The image of a fixed point object inside water (mw = 1/3) is formed by a thin convex lens placed just outside the plane water surface at a distance of 9 cm from the lens. When this lens is put just inside the water surface, the image of the object is formed at a distance of 10 cm from the lens. Find the focal length of the lens given that the refractive index of the material of the lens is 1.5.
(a)20 cm
(b)60 cm
(c)30 cm
(d)50 cm
Ans (d)
4.
In the given figure there are two thin lenses of same focal length f arranged with their principal axes inclined at an angle a. The separation between the optical centers of the lenses is 2f. A point object lies on the principal axis of the convex lens at a large distance to the left of convex lens. Find the co-ordinates of the final image formed by the system of lenses taking O as the origin of co-ordinate axes.
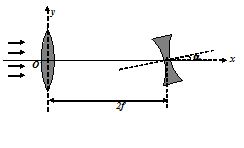
(a) \left( {f\left( {\frac{{4+2\cos \alpha }}{{4+\cos \alpha }}} \right),\,\,\,0} \right)
(b) \left( {f\left( {\frac{{2+2\cos \alpha }}{{2+\cos \alpha }}} \right),\,\,\,0} \right)
(c) \left( {f\left( {\frac{{1+2\cos \alpha }}{{1+\cos \alpha }}} \right),\,\,\,0} \right)
(d) \left( {f\left( {\frac{{3+2\cos \alpha }}{{3+\cos \alpha }}} \right),\,\,\,0} \right)
Ans (c)
