Video Lecture
Theory For Making Notes
Reflection by Spherical mirrors
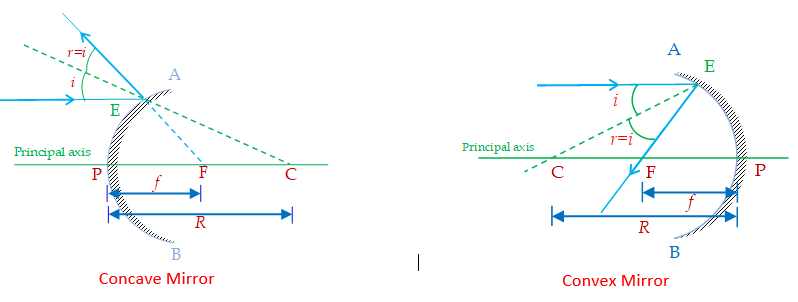
A spherical mirror is a part of a spherical reflecting surface. When the reflection takes place from the inner surface and outer surface is polished or silvered, the mirror is known as concave mirror. When the reflection takes place from the outer surface and the inner surface is polished or silvered, the mirror is known as convex mirror as shown in the diagram shown below
Important Terms Used in Spherical Mirrors
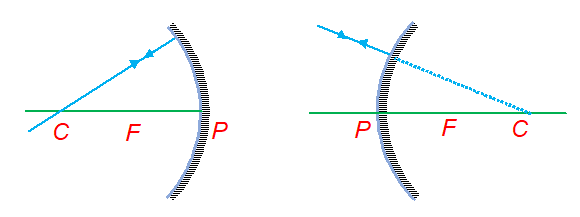
- The centre of curvature of a mirror is the centre of the spherical surface of which the mirror is a part (point C in figure)
- The radius of curvature R is the radius of spherical surface of which the mirror is a part (distance CP in figure).
- The pole of the mirror is the point at which the principal axis intersect the mirror. Normally when the rays fall symmetrically on the mirror then the geometrical centre of the mirror serves as pole. (The point P in the figure).
- The principal axis is the line joining the centre of curvature C with the pole P of the mirror
- The principal focus is the point on the principal axis, through which a ray of light parallel to the principal axis, after reflection, passes (in case of concave mirror) or appears to pass (in case of concave mirror) (point F in figure)
- Focal length is the distance between the pole P and the principal focus F. It is represented by f (distance PF in figure). For a spherical mirror of small aperture, the focal length is half of the radius of curvature (f = R/2).
The aperture is the diameter of the mirror (length AB in figure). It may be used to find the maximum effective area of mirror which receives the light rays when they are incident parallel to the principal axis.
Mirror formula
For all spherical mirrors with small aperture the following relation holds good
\displaystyle \frac{1}{u}+\frac{1}{v}=\frac{2}{R}=\frac{1}{f}
Where,
u = distance of the object from the pole of mirror,
v = distance of the image from the pole of mirror,
f = focal length of the mirror and R = radius of curvature the mirror
Newton’s Formula
In case of spherical mirrors if object distance ( {{x}_{1}}) and image distance {{x}_{2}}) are measured from focus instead of pole,
u=(f+{{x}_{1}}) and u=(f+{{x}_{2}}). Thus, the mirror formula
\frac{1}{v}+\frac{1}{u}=\frac{1}{f} reduces to \frac{1}{{(f+{{x}_{2}})}}+\frac{1}{{(f+{{x}_{1}})}}=\frac{1}{f}
which on simplification gives {{f}^{2}}={{x}_{1}}{{x}_{2}}
This is called Newton’s formula.
Working Rules for image formation
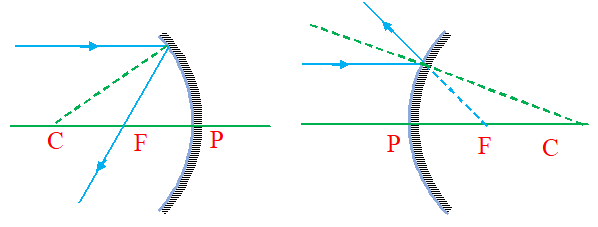
The reflection of light rays and formation of images are shown with the help of ray diagrams. Some typical incident rays and the corresponding reflected rays are shown below.
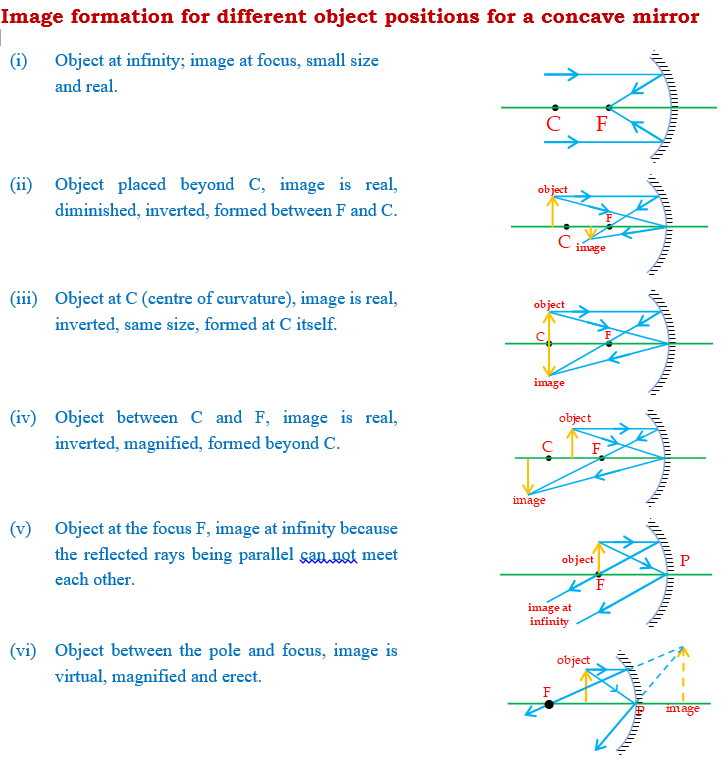
(i) A ray passing parallel to the principal axis after reflection from the spherical mirror passes or appears to pass through its focus (by the definition of focus)
(ii)A ray passing through or directed towards focus after reflection from the spherical mirror becomes parallel to the principal axis (by the principle of reversibility of light).
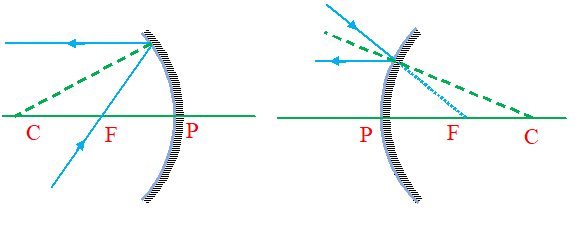
(iii)A ray passing through or directed towards the centre of curvature, after reflection from the spherical mirror, retraces its path (as for it \displaystyle \angle i= 0 and so \displaystyle \angle r = 0)
In case of image formation unless stated otherwise, object is taken to be real and we consider only rays that are close to the principal axis and that make small angles with it. Such rays are called paraxial rays. In practice this condition may be achieved by using a mirror whose size is much smaller than the radius of curvature of the surface. Otherwise the image will be distorted.
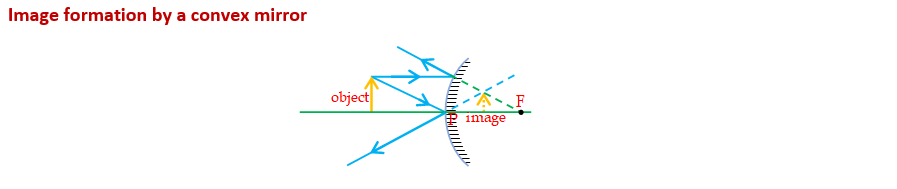
(i) In case of convex mirror, when an object is placed in front of the mirror (anywhere), then the image is always formed behind the mirror.
(ii) The image is always virtual, erect and smaller in size in the case of a real object.
(iii) As the object is taken away from the pole, the size of the image goes on decreasing and when the object lies at infinity, a point size image is formed.
(iv) The convex mirror always forms a diminished and erect image, irrespective of the position of the object. Because of this, it is used as a rear view mirror.
Sign convention
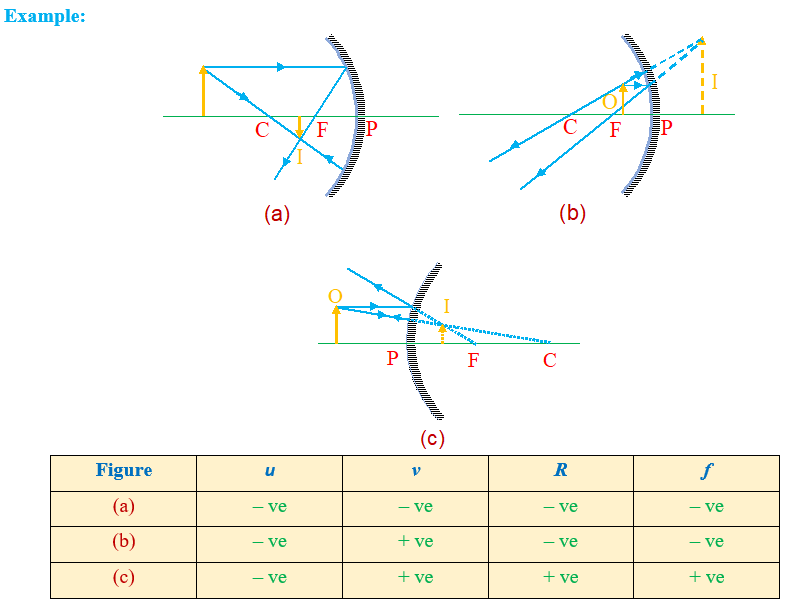
(i)
All the distances along the principal axis (i.e., u, v and f) are measured with respect to pole of a mirror.
(ii)
Distances measured in the direction of incident light ray are taken as positive and those measured opposite to the direction of incident light ray as negative.
(iii)
The distances (heights) measured above the principal axis are taken as positive while distances below the principal axis are taken as negative.
(iv)
According to this sign convention, the focal length and radius of curvature of a concave mirror are negative, while those of convex mirror are positive.
Different Types Of Magnification
Linear Magnification due to a mirror
(i)
Transverse or linear magnification m is defined as
\displaystyle m=\frac{{\text{size}\,\,\text{of}\,\,\text{image}\,\,\text{(I)}}}{{\text{size}\,\,\text{of}\,\,\text{object}\,\,\text{(O)}}}
(ii)
It can be proved that for both concave and convex mirrors:
\displaystyle m=-\frac{v}{u}
or \displaystyle m=\frac{f}{{f-u}}
or \displaystyle m=\frac{{f-v}}{f}
(iii)
(a) If \displaystyle \left| m \right|>1, the image is enlarged,
(b) If \displaystyle \left| m \right|=1, the image is of same size,
(c) If \displaystyle \left| m \right|<1, the image is diminished,
(d) If m > 0, the image is erect,
(e) If m < 0, the image is inverted
Longitudinal Magnification / Axial magnification due to a mirror
Case-1
When a object `O’ of finite length AB lies along the principle axis.
Let the two ends of the object `A’ and `B’ are at a distance of u2 and u1 from the pole.
Hence the length of object AB = \displaystyle {{u}_{2}}-{{u}_{1}}
Let the image of Point A is at A’ and that of B is at B’. Therefore A’B’ is the length of the image. Hence A’B’ = \displaystyle {{v}_{2}}-{{v}_{1}}
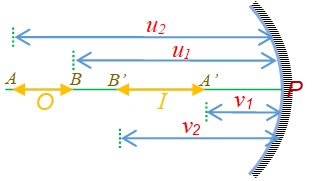
then the longitudinal or axial magnification
{{m}_{{axial}}}=\frac{{A’B'(Length\text{ }of\text{ }image)}}{{AB(Length\text{ }of\text{ object})}}=\frac{{-({{v}_{2}}-{{v}_{1}})}}{{({{u}_{2}}-{{u}_{1}})}}
if {{u}_{1}} and {{u}_{2}} are given we can find {{v}_{1}} and {{v}_{2}} from mirror formula
Case-2
When a very small object `O’ lies along the principle axis.
Then the length of the object AB = du
And the length of the image A’B’ = dv
hence {{m}_{{axial}}}=\frac{{A’B'(Length\text{ }of\text{ }image)}}{{AB(Length\text{ }of\text{ object})}}=\frac{{-dv}}{{du}}
we know the mirror formula is
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}.
Differentiating this (Taking focal length f as constant) we get
-\frac{{dv}}{{du}}={{\left( {\frac{v}{u}} \right)}^{2}}
But by using mirror formula we can prove that
{{\left( {\frac{v}{u}} \right)}^{2}}={{\left( {\frac{f}{{f-u}}} \right)}^{2}}={{\left( {\frac{{f-v}}{f}} \right)}^{2}}
hence finally
{{m}_{{axial}}}=-\frac{{dv}}{{du}}={{\left( {\frac{v}{u}} \right)}^{2}} ={{\left( {\frac{f}{{f-u}}} \right)}^{2}}={{\left( {\frac{{f-v}}{f}} \right)}^{2}}
Also
{{m}_{{axial}}}=-\frac{{dv}}{{du}}={{\left( {\frac{v}{u}} \right)}^{2}}=m_{{linear}}^{2} ( \therefore \text{ }\,{{m}_{{linear}}}=-\frac{v}{u})
Areal magnification Due To Mirror
If a 2D-object is placed with it’s plane perpendicular to principle axis. It’s Areal magnification
{{m}_{{areal}}}=\frac{{\text{Area}\,\text{of}\,\text{image}\,({{A}_{i}})}}{{\text{Area}\,\text{of}\,\text{object}\,({{A}_{o}})}}
\Rightarrow \,\,\,{{m}_{{areal}}}=m_{{linear}}^{2}=\frac{{{{A}_{i}}}}{{{{A}_{o}}}}
Illustration
A concave mirror has a radius of curvature of 24 cm. How far is an object from the mirror if the image formed is:
(a) virtual and 3.0 times the size of the object.
(b) real and 3.0 times the size of the object.
Solution
Given R = – 24 cm ( concave mirror)
Hence, f = \displaystyle \frac{R}{2} = – 12 cm
(a)
Image is virtual and 3 times larger. Hence, u is negative and v is positive. Simultaneously, \displaystyle |v|\,\,=\,\,3\,\,|u|. So let,
u = – x
then v = + 3x
Substituting in the mirror formula \displaystyle \frac{1}{v}+\frac{1}{u}=\frac{1}{f}, we have
\displaystyle \frac{1}{{3x}}-\frac{1}{x}=\frac{1}{{-12}}
or x = 8 cm
(b)
Image is real and three times larger. Hence u and v both negative and \displaystyle |v|\,\,=\,\,3|u|.
So let,
u = – x
then, v = – 3x
Substituting in mirror formula, we have
\displaystyle \frac{1}{{-3x}}-\frac{1}{x}=-\frac{1}{{12}}
or x = 16 cm
hence object distance is 16 cm.
Illustration
An object is placed in front of a convex mirror at a distance of 50 cm. A plane mirror is introduced covering the lower half of the convex mirror. If the distance between the object and the plane mirror is 30 cm, it is found that there is no parallax between the images formed by the two mirrors. Calculate the radius of curvature of the convex mirror.
Solution
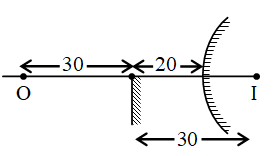
Since the object is at 30 cm in front of the plane mirror, its image will be formed at 30 cm behind the plane mirror. Therefore distance of image from the convex mirror = 10 cm
Now for convex mirror
u = – 50, \displaystyle v=+\frac{1}{{10}}
\displaystyle \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
\displaystyle \frac{1}{{10}}-\frac{1}{{50}}=\frac{1}{f}
or f = 12.5 cm
Illustration
A thin rod of length f/3 is placed along the optic axis of a concave mirror of focal length f such that its image which is real and elongated just touches the rod. Calculate the magnification of mirror.
Solution
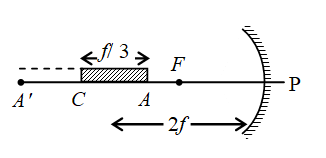
The image of the rod placed along the optic axis will touch the rod only when one end of the rod AC is at the centre of curvature of the concave mirror.
As shown in the figure if AC = f/3 and PC = 2f.
Since the end C of the rod lies at centre of curvature of the rod, its image will form at C itself. Now for the end A of the rod
u = 2f – f/3 = \displaystyle \frac{{5f}}{3}
Now \displaystyle \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
\displaystyle \frac{1}{v}+\frac{1}{{-5f/3}}=\frac{1}{{-f}}
\displaystyle \frac{1}{v}=\frac{3}{{5f}}-\frac{1}{f}=-\frac{2}{{5f}}
or \displaystyle v=-\frac{{5f}}{2}
or \displaystyle P{A}’=\frac{{5f}}{2}
hence the Length of the image = \displaystyle \frac{{5f}}{2}-2f=\frac{f}{2}
Therefore magnification = \displaystyle \frac{{C{A}’}}{{CA}}=\frac{{f/2}}{{f/3}}=1.5
Illustration
An object is placed in front of a concave mirror at a distance of 7.5 cm from it. If the real image is formed at a distance of 30 cm from the mirror, find the focal length of the mirror. What would be the focal length if the image is virtual.
Solution
Case I: When the image is real.
We have u = – 7.5 cm; v = – 30 cm; f = ?
We know \frac{1}{v}\,+\,\frac{1}{u}\,=\,\frac{1}{f}
or, f = \frac{{uv}}{{u\,+\,v}} = = – 6 cm
The negative sign shows that the spherical mirror is concave.
Case II: When the image is virtual
In this case, u = – 7.5 cm, v = + 30 cm
We know \frac{1}{v}\,+\,\frac{1}{u}\,=\,\frac{1}{f}
or, f = \frac{{uv}}{{u\,+\,v}}\,=\,\frac{{(-75)\,\,(30)}}{{-7.5\,+\,30}}= – 10 cm
Illustration
An object 5 cm high is placed 30 cm from a convex mirror whose focal length is 20 cm. Find the position, size and nature of the image.
Solution
We have u = – 30 cm; v = ? f = + 20 cm
We know \frac{1}{v}\,+\,\frac{1}{u}\,=\,\frac{1}{f}
or, v = \frac{{uf}}{{u\,-\,f}} = \frac{{(-30)\,\,(+20)}}{{-30\,-\,20}} + 12 cm
The image is formed 12 cm behind the mirror. It is virtual and erect.
Now, m = \frac{\mathbf{I}}{\mathbf{O}}\,=\,-\,\frac{v}{u}\,=\,-\,\frac{{12}}{{-30}}
or, I = \frac{2}{5}\,\times \,\,\,O\,\,=\,\,\frac{2}{5}\,\times \,\,5 = + 2 cm
Hence the height of the image = + 2 cm
The positive sign indicates that the image is erect.
Illustration
An object 0.2 cm high is placed 15 cm from a concave mirror of focal length 5 cm. Find the position and size of the image.
Solution
We have u = –15 cm; v = ? f = – 5 cm
We know that \frac{1}{v}\,+\,\frac{1}{u}\,=\,\frac{1}{f}
or, v = \frac{{u\,f}}{{u\,-\,f}}\,=\,\frac{{(-15)\,(-5)}}{{-15\,+\,5}} = – 7.5 cm
The image is formed at a distance of 7.5 cm in front of mirror.
Now, m = \frac{I}{O}\,=\frac{-v}{u}
or, \frac{I}{O}\,=\,-\,\frac{{(-7.5)}}{{(-15)}}
or, I=\frac{1}{2}(-0.2)=-0.1\,\mathbf{cm}
The negative sign indicates that image is inverted.
Illustration
Two rays are incident on a spherical concave mirror of radius R = 5cm parallel to its optical axis at distances 3 cm and h2 = 4cm. Determine the value \Delta xif distance between the points at which these rays intersect the optical axis after being reflected from the mirror is \frac{{\Delta x}}{{24}} cm.
Solution
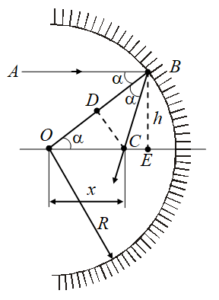
Let O be the centre of the spherical surface of the mirror, ABC the ray incident at a distance BE from the mirror axis, and OB = R. From the right triangle OBE, we find that \sin \alpha =h/R. The triangle OBC is isosceles since \angle ABO=\angle BOCand \angle BOC=\angle ABO as alternate-interior angles. Hence OD = BD = R/2. From the triangle ODC, we obtain
x=\frac{R}{{2\cos \alpha }}=\frac{{{{R}^{2}}}}{{2\sqrt{{{{R}^{2}}-{{h}^{2}}}}}}
{{x}_{1}}-{{x}_{2}}=\frac{{25}}{{24}} cm \therefore \,\,\Delta x=25
Illustration
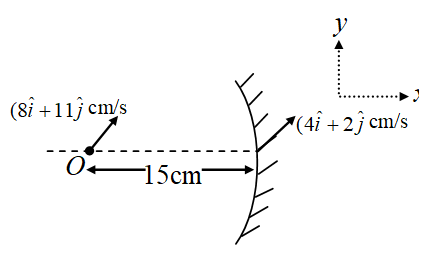
A point object is located at a distance 15 cm from the pole of a concave mirror of focal length 10 cm on its principal axis is moving with a velocity (8\hat{i}+11\hat{j})cm/s and velocity of mirror is (4\hat{i}+2\hat{j})cm/s as shown. If \vec{V} is the velocity of image. Then find the value of \left| {\ \vec{V}\ } \right| (in cm/s)
Solution
{{\vec{V}}_{{\text{obj,}\ \text{mirror}}}}=4\hat{i}+9\hat{j}
\frac{{dx}}{{dt}}=4,\frac{{dy}}{{dt}}=9
u=-x
-\frac{1}{{10}}=\frac{1}{V}+\frac{1}{{-x}}
V=\frac{{-10x}}{{x-10}}
{{V}_{{1x}}}=\frac{{dV}}{{dt}}={{\left( {\frac{{10}}{{x-10}}} \right)}^{2}}\left( {\frac{{dx}}{{dt}}} \right)
{{V}_{{1x}}}=-16
m=-\frac{V}{{-x}}=\frac{{-10}}{{x-10}}=\frac{{y_{1}^{0}}}{y}
{{V}_{{1y}}}=-\left( {\frac{{10}}{{x-10}}} \right)\frac{{dy}}{{dt}}
{{V}_{{1y}}}=-18
{{\vec{V}}_{{\text{image,mirror}}}}=-16\hat{i}-18\hat{j}
{{\vec{V}}_{{\text{image}}}}=-12\hat{i}-16\hat{j}
\left| V \right|=20 cm/s
Practice Questions (Basic Level)
Q.1
A concave mirror of focal length f produces an image n times the size of the object. If the image is real then the distance of the object from the mirror is
(a) \left( {n-1} \right)f
(b) \frac{{\left( {n-1} \right)}}{n}f
(c) \frac{{\left( {n+1} \right)}}{n}f
(d) \left( {n+1} \right)f
Ans. (c)
Q.2
For a concave mirror of focal length 20 cm, if the object is at a distance of 30 cm from the pole, then the nature of the image and its magnification will be
(a) real and –2
(b) virtual and –2
(c) real and +2
(d) virtual and +2
Ans. (a)
Q.3
The relation between lateral magnification m, object distance u and focal length f of a spherical mirror is
(a) m=\frac{{f-u}}{f}
(b) m=\frac{f}{{f+u}}
(c) m=\frac{{f+u}}{f}
(d) m=\frac{f}{{f-u}}
Ans. (d)
Q.4
An object 1 cm tall is placed in front of a mirror at a distance of 4 cm. In order to produce an upright image of 3cm height one needs a
(a) convex mirror of radius of curvature 12 cm
(b) concave mirror of radius of curvature 12 cm
(c) concave mirror of radius of curvature 4 cm
(d) plane mirror of height 12 cm\
Ans. (b)
Q.5
An object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by the mirror is
(a) Real and at 20 cm from the mirror
(b) Virtual and at 20 cm from the mirror
(c) Virtual and at (20/3) cm from the mirror
(d) Real and at (20/3) cm from the mirror
Ans. (c)
Q.6
An object is placed in front of a convex mirror at a distance of 50 cm. A plane mirror is introduced covering the lower half of the convex mirror. If the distance between the object and the plane mirror is 30 cm, there is no parallax between the images formed by the two mirrors. The radius of curvature of the convex mirror (in cm) is
(a) 60 (b) 50 (c) 30 (d) 25
Ans. (d)
Q.7
Rays are converging towards a convex mirror, final image will be
(a) real
(b) virtual
(c) may be real or virtual
(d) image will not form
Ans. (a)
8.
A concave mirror has a focal length of 36cm. At what position should an object be placed for its image to be erect and be magnified by a factor of three?
(a) 20 cm
(b) 22 cm
(c) 24 cm
(d) 30 cm
Ans (c)
9.
An object of height 0.5 cm is placed 18 cm from a curved mirror. The erect image is 2 cm high. What is the focal length of the mirror ?
(a) 50 cm
(b) 10 cm
(c) 30 cm
(d) 24 cm
Ans (d)
10.
A real object 27 cm from a concave mirror produces a real image 15.9 cm from the mirror. What is the image position for an object placed 15 cm from the mirror?
(a) 50 cm
(b) 10 cm
(c)30 cm
(d)100 cm
Ans (c)
11.
An object is 60 cm from a concave mirror. The size of the real image is 40% of the size of the object. What is the radius of curvature of the mirror?
(a)34.3 cm
(b)32.0 cm
(c) 25.5 cm
(d) 50.0 cm
Ans (a)
12.
A convex mirror of focal length 30cm produces an image with a magnification
of 0.4. Where is the object?
(a)45 cm
(b)90 cm
(c)25 cm
(d) 50 cm
Ans (a)
13.
A concave mirror produces an image 40% larger when a real object is 20cm from the mirror. Determine the possible focal lengths of the mirror.
(a)10.5 cm; 50 cm
(b)11.7 cm; 70 cm
(c)12.5 cm; 80 cm
(d)13.7 cm; 90 cm
Ans (c)
14.
The longitudinal magnification `mL’ for a very small object and linear magnification `m’ for a mirror are related as
(a)mL=m
(b) mL=(m)1/2
(c)mL=m2
(d) mL=m3.
Ans : (c)
Practice Questions (JEE Main Level)
Q.1
An object is placed at a distance u from a concave mirror and its real image is received on a screen placed at a distance of v from the mirror. If f is the focal length of the mirror, then the graph between 1/v versus 1/u is

Ans (b)
Q.2
In the figure shown, the image of a real object is formed at point I. AB is the principal axis of the mirror. The mirror must be
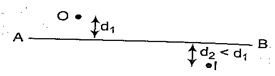
(a) concave and placed towards right of I
(b) concave and placed towards left of I
(c) convex and placed towards right of I
(d) convex and placed towards left of I
Ans (a)
Q.3
An object is placed in front of a concave mirror of focal length f as shown in figure. Choose the correct shape of the image.

Ans (b)
Q.4
A point object is kept between a plane mirror and a concave mirror facing each other. The distance between the mirrors is 22.5 cm. The radius of curvature of the concave mirror is 20 cm. What should be the distance of the object from the concave mirror so that after two successive reflections the final image is formed on the object itself? (Consider first reflection from concave mirror.)
(a) 5 cm (b) 15 cm (c) 10 cm (d) 7.5 cm
Ans. (b)
Q.5
A luminous point object is moving along the principal axis of a concave mirror of focal length 12 cm towards it. When its distance from the mirror is 20 cm its velocity is 4 cm/s. The velocity of the image in cm/s at that instant is
(a) 6, towards the mirror
(b) 6, away from the mirror
(c) 9, away from the mirror
(d) 9, towards the mirror
Ans. (c)
Q.6
The passenger side-view mirror on an automobile often has the notation ‘objects seen in mirror are closer than they appear’. Is the image really farther away than the object?
(a) Yes, the image is smaller and farther away than the object.
(b) No, the image is smaller and closer than the object.
(c) No, the image is larger and closer than the object.
(d) Yes, the image is larger and farther away than the object.
Ans. (b)
Q.7
Focal length of a convex mirror is 10 cm
(a) image of an object placed at 20 cm is also at 20 cm
(b) image of an object placed at 10 cm is at infinity
(c) both (a) and (b) are wrong
(d) both (a) and (b) are correct
Ans. (c)
Q.8
A concave mirror has a focal length 20 cm. The distance between the two positions of the object for which the image size is double of the object size is
(a) 20 cm (b) 40 cm (c) 30 cm (d) 60 cm
Ans. (a)
Q.9
An infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is at a distance \displaystyle u\,>\,f from the mirror. Its image will have a length
(a) \displaystyle \frac{{uf}}{{u-f}}
(b) \displaystyle \frac{{uf}}{{u+f}}
(c) \displaystyle \frac{{{{f}^{2}}}}{{u+f}}
(d) \displaystyle \frac{{{{f}^{2}}}}{{u-f}}
Ans. (d)
Q.10
An object is placed infront of a concave mirror of focal length f. A virtual image is formed with a magnification of 2. To obtain a real image of same magnification, the object has to move by a distance
(a) f (b) f/2 (c) 3f/2 (d) 2f/3
Ans. (a)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
