Video Lecture
Theory For Making Notes
Young’s Double-slit Experiment
One of the earliest demonstrations of such interference effect was first done by Thomas Young in 1801, establishing the wave character of light. Young allowed sunlight to fall on a pinhole S0, punched in a screen A as shown in Figure. The emergent light spreads out and falls on pinholes {{S}_{1}} and {{S}_{2}}, punched in the screen B.(To show distinctly the light from {{S}_{1}} and {{S}_{2}} are shown in different colors in the diagram). Pinholes {{S}_{1}} and {{S}_{2}} act as coherent sources. Again, two overlapping spherical waves expand into space to the right of screen B. Figure shows how Young produced an interference pattern by allowing the waves from pinholes {{S}_{1}} and {{S}_{2}} to overlap on screen C.
Analytical treatment of Young’s Double slit experiment
To analyze the interference pattern and investigate the spacing of the interference fringes, consider the geometry in figure. Let S be a narrow slit illuminated by monochromatic light, and {{S}_{1}} and {{S}_{2}} two parallel narrow slits very close to each other and equidistant from S.
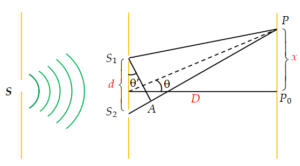
The light from S arrive at {{S}_{1}} and {{S}_{2}} in the same phase. Beyond {{S}_{1}} and {{S}_{2}} the waves proceed as if they started from {{S}_{1}} and {{S}_{2}} with the same phase because the two slits are equidistant from S.
It is assumed that the waves start out at the same phase, because the two slits {{S}_{1}} and {{S}_{2}} are equidistant from S. Furthermore, the amplitudes are the same, because {{S}_{1}} and {{S}_{2}} are the same size slits and very close to each other. Hence these waves produce an interference pattern on a screen placed parallel to {{S}_{1}} and {{S}_{2}}.
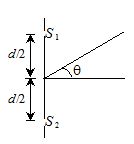
To find the intensity at a point P on the screen, we join {{S}_{1}}P and {{S}_{2}}P. The two waves arrive at P from {{S}_{1}} and {{S}_{2}} having traversed different paths {{S}_{1}}P and {{S}_{2}}P. Let us calculate this path difference {{S}_{2}}P – {{S}_{1}}P. Let,
x = distance of P from Po, the central point on the screen
d = separation of two slits {{S}_{1}} and {{S}_{2}}
D = distance of slits from the screen.
The corresponding path difference is the distance {{S}_{2}}A in figure, where the line {{S}_{1}}A has been drawn to make {{S}_{1}} and A equidistant from P. As Young’s experiment is usually done with \displaystyle D>>d, the angle \displaystyle \theta and \displaystyle \theta’ are nearly same and they are small.
Hence, we may assume triangle {{S}_{1}}A{{S}_{2}} as a right-angled triangle
and {{S}_{2}} \displaystyle A=dsin\theta ‘=dsin\theta ~=~dtan\theta ; as for small \displaystyle \theta , \displaystyle sin\theta =\text{ }tan\theta .
As can be seen from the figure, \displaystyle tan\theta =\frac{x}{D}.
therefore \displaystyle {{S}_{2}}P-{{S}_{1}}P={{S}_{2}}A=\frac{{xd}}{D}
Now the intensity at the point P is a maximum or minimum according as the path difference
{{S}_{2}}P – {{S}_{1}} P is an integral multiple of wavelength or an odd multiple of half wavelength. Hence, for bright fringes (maxima)
\displaystyle {{S}_{2}}P-{{S}_{1}}P=\frac{{xd}}{D}=0,\ \pm \lambda ,\ \pm 2\lambda ,\ \pm 3\lambda ,\,\,\pm 4\lambda …=n\lambda
Hence \displaystyle x=\frac{{n\lambda D\ \ }}{d}
(hers x gives the position of bright fringes from the central bright fringe)
where \displaystyle n=0,\pm 1,\pm 2,\pm 3,…
The number n is called the order of the fringe. Thus the fringes with n = 0, 1, 2, …. etc. are called zero, first, second…..etc. orders. The zeroth order fringe corresponds to the central maximum, the first order fringe (n = 1) corresponds to the first bright fringe on either side of the central maximum, and so on. For dark fringes (minima),
We know that \displaystyle {{S}_{2}}P-{{S}_{1}}P=\frac{{xd}}{D}
For dark fringe \displaystyle \frac{{xd}}{D} =\pm \frac{\lambda }{2},\pm \ \frac{{3\lambda }}{2},\pm \ \frac{{5\lambda }}{2}…=\left( {n-\frac{1}{2}} \right)\lambda
Hence \displaystyle x=\left( {2n-1} \right)\frac{{\lambda D}}{{2d}} (hers x gives the position of dark fringes from the central bright fringe)
where \displaystyle n=\pm 1,\pm 2,\pm 3,…
Fringe Width
It is the linear separation between the centres of two consecutive bright or dark fringe.
If \displaystyle {{x}_{n}} and \displaystyle {{x}_{n+1}} denote the distances of nth and (n + 1)th bright fringes, then
\displaystyle {{x}_{n}}=n\lambda\frac{D}{d}
and \displaystyle {{x}_{{n+1}}}=(n+1)\lambda\frac{D}{d}
The spacing between the nth and (n+1)th fringes (bright) is given by
\displaystyle \omega ={{x}_{{n+1}}}-{{x}_{n}}
so \displaystyle \omega=(n+1)\lambda\frac{D}{d} -n\lambda\frac{D}{d}
hence \displaystyle \omega=\frac{{\lambda D}}{d}
It is independent of n. Hence, the spacing between any two consecutive bright fringes is the same. Similarly, it can be shown that the spacing between two dark fringes is also \displaystyle \frac{{\lambda D}}{d}. The spacing between any two consecutive bright or dark fringes is called the fringe-width, which is denoted by \displaystyle \omega. Thus
\displaystyle \omega =\frac{{\lambda D}}{d}
One also finds, by experiment, that fringe-width
(i) varies directly with D
(ii) varies directly with the wave-length \displaystyle \lambda of the light used
(iii) varies inversely with the distance d between the slits
(iv) varies inversely with refractive index of medium used between slits and screen
The fringe-widths are so fine that to see them, one usually uses magnifier or eye-piece.
Intensity Distribution in the Fringe-System
To find the intensity, we rewrite Eq.,
\displaystyle I=I_{1}^{{}}+I_{2}^{{}}+2\sqrt{{{{I}_{1}}{{I}_{2}}}}\cos \phi
or \displaystyle I=a_{1}^{2}+a_{2}^{2}+2{{a}_{1}}{{a}_{2}}\cos \phi
If the slits are identical in shape and size then we can take \displaystyle {{a}_{1}}={{a}_{2}}=a
hence \displaystyle I=2{{a}^{2}}(1+\cos \phi )
or \displaystyle I=4{{a}^{2}}{{\cos }^{2}}\frac{\phi }{2}
Here \displaystyle 4{{a}^{2}} is the maximum intensity at the bright fringe and we can denote it by \displaystyle {{I}_{o}} ,
so finally we get \displaystyle I={{I}_{o}}{{\cos }^{2}}\frac{\phi }{2}
At the bright fringe the phase difference is given by \displaystyle \phi =\text{ }0,\text{ }2\pi ,\text{ }4\pi \ldots .,
this gives \displaystyle I=4{{a}^{2}} i.e at bright fringe the intensity is 4 times the intensity of either beam.
At the dark fringe the phase difference is given by If \displaystyle \phi =\text{ }3\pi ,\text{ }5\pi \ldots ., ,so the intensity is zero.
In between, the intensity varies as \displaystyle I={{I}_{o}}{{\cos }^{2}}\frac{\phi }{2}.
Figure shows a plot of the intensity against the phase difference. Thus, as shown in figure, the intensity in the interference pattern varies between \displaystyle I=4{{a}^{2}} ( \displaystyle {{I}_{o}}) and zero.
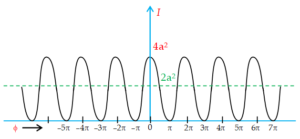
Now each beam, acting separately, would
contribute \displaystyle I={{a}^{2}} , and so, without interference, we would have a uniform intensity of \displaystyle I=2{{a}^{2}} , as indicated by the broken line.
Average Intensity
Let us obtain the average intensity on the screen for \displaystyle \pi fringes. We have
\displaystyle {{I}_{{average}}}=\frac{{\int\limits_{0}^{\pi }{{Id\phi }}}}{{\int\limits_{0}^{\pi }{{d\phi }}}}
\displaystyle =\frac{{\int\limits_{0}^{\pi }{{\left( {4{{a}^{2}}{{{\cos }}^{2}}\frac{\phi }{2}} \right)d\phi }}}}{{\int\limits_{0}^{\pi }{{d\phi }}}}
\displaystyle =\frac{{\int\limits_{0}^{\pi }{{(2{{a}^{2}}+2{{a}^{2}}\cos \phi )d\phi }}}}{{\int\limits_{0}^{\pi }{{d\phi }}}}\ \ \ \left( {\because \ \ 1+\cos \theta ={{{\cos }}^{2}}\frac{\theta }{2}} \right)
\displaystyle =\frac{{[2{{a}^{2}}\phi +2{{a}^{2}}\sin \phi ]_{0}^{\pi }}}{{[\phi ]_{0}^{\pi }}}
\displaystyle =\frac{{2{{a}^{2}}\pi }}{\pi }
\displaystyle =2{{a}^{2}}
Thus, the average intensity is equal to the sum of the separate intensities. That is whatever energy apparently disappears at the minima is actually present at the maxima. Hence there is no net loss or gain in the energy of the medium during interference and therefore there is no violation of the law of conservation of energy in the phenomenon of interference.
Spl.case : For two waves of same intensity `I’ and having a constant phase difference of \displaystyle \phi , the resultant intensity is given by
\displaystyle {{I}_{R}}=2I+2I\cos \phi
\displaystyle (\because \ \ {{I}_{1}}={{I}_{2}}=I)
\displaystyle =2I(1+\cos \phi )
\displaystyle hence\text{ }{{I}_{R}}=4I{{\cos }^{2}}\frac{\phi }{2}
Therefore, we find that when two waves of the same frequency travel in approximately the same direction and have a phase difference that remains constant with the passage of time, the resultant intensity of light in not distributed uniformly in space means we do not get a uniform light in space.(Here for better understanding the space can be considered as a screen )The non-uniform distribution of the light intensity due to the superposition of two waves is called interference.
At some points in the space or screen where the phase difference \displaystyle \phi is equal to \displaystyle 2n\pi the intensity becomes maximum and the interference at these points is called constructive interference. At some other points in the space or screen where the phase difference \displaystyle \phi is equal to \displaystyle \left( {2n+1} \right)\pi the intensity is minimum and the interference at these points is called destructive interference.
The average intensity on the screen is exactly what should exist in the absence of interference. Means there is no net loss or gain of energy but there is a redistribution of energy during interference.
Displacement of Fringes
When a thin transparent plate, say of glass or mica, is introduced in the path of one of the two interfering beams, as shown in figure. It is observed that the entire fringe-pattern is displaced to a point towards the beam in the path of which the plate is introduced.
Suppose a thin transparent plate of thickness t and refractive index \mu is introduced in the path of one of the constituent interfering beams of light (say in the path of {{S}_{1}}P, shown in figure). Now, light from {{S}_{1}} travel partly in air and partly in the plate. For the light path from {{S}_{1}} to P, the distance traveled in air is ({{S}_{1}}P – t), and that in the plate is t.Suppose, c and v be the velocities of light in the air and in the plate, respectively. If the time taken by light beam to reach from {{S}_{1}} to P is, T, then
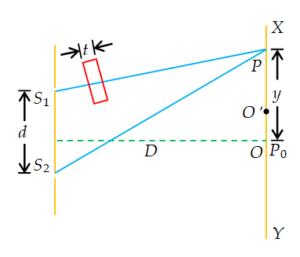
\displaystyle T=\frac{{{{S}_{1}P}-t}}{c}+\frac{t}{v}
or, \displaystyle T=\frac{{{{S}_{1}}P-t}}{c}+\frac{{\mu t}}{c}\ \ \ \left( {\because \ \ \ v=\frac{c}{\mu }} \right)
\displaystyle =\frac{{{{S}_{1}}P+(\mu -1)\ t}}{c}
Thus the effective path in air from {{S}_{1}} to P is [{{S}_{1}}P + (\mu – 1)]t i.e., the air path {{S}_{1}}P is increased by an amount (\mu – 1)t , due to the introduction of the plate of material of refractive index, \mu .
Let O be the position of the central bright fringe in the absence of the plate, the optical paths {{S}_{1}}O and {{S}_{2}}O being equal. On introducing the plate, the two optical paths become unequal. Therefore, the central fringe is shifted to \displaystyle O’, such that at \displaystyle O’ the two optical paths become equal. A similar argument applies to all the fringes. Now, at any point P, the effective path difference is given by \Delta x
where \Delta x = {{S}_{2}}P – [{{S}_{1}}P + \displaystyle (\mu – 1)t]
= ({{S}_{2}}P – {{S}_{1}}P) – \displaystyle (\mu – 1)t
As we know in the absence of thin sheet.
\displaystyle {{S}_{2}}P-{{S}_{1}}P=\frac{{xd}}{D}
Hence effective path difference \Delta x at \displaystyle P=\frac{{xd}}{D}-(\mu -1)t
If the point P is to be the centre of the nth bright fringe, the effective path difference should be equal to \displaystyle n\lambda i.e.,
\displaystyle \frac{{{{x}_{n}}d}}{D}-(\mu -1)t=n\lambda
or
\displaystyle {{x}_{n}}=\frac{D}{d}[n\lambda +(\mu -1)t] …(i)
In the absence of the plate (t = 0), the distance of the nth bright fringe from O is \displaystyle \frac{{n\lambda D}}{d}.
Therefore displacement `S’ of the nth bright fringe is given by the difference of the two positions of nth fringe i.e with plate and without plate
hence \displaystyle S=\frac{D}{d}[n\lambda +(\mu -1)t]-\frac{{n\lambda D}}{d}
\displaystyle \Rightarrow \text{ }S=\frac{D}{d}[(\mu -1)t] …(ii)
The shift is independent of the order of the fringe, showing that shift is the same for all the bright fringes. Similarly, it can be shown that the displacement of any dark fringe is also given by Eq. (ii). Thus, the entire fringe-system is displaced through a distance \displaystyle \frac{D}{d}(\mu -1)t towards the side on which the plate is placed. The fringe-width is given by :
\displaystyle \beta ={{x}_{{n+1}}}-{{x}_{n}}
\displaystyle =\frac{D}{d}[(n+1)\lambda +(\mu -1)t]-\frac{D}{d}[n\lambda +(\mu -1)t] (see Eq. (i))
\displaystyle =\frac{{D\lambda }}{d}
which is the same as before the introduction of the plate.
This phenomena of shift in fringes enables us to determine the thickness of extremely thin transparent sheets (like that of mica) by measuring the shift of the fringe system.
Illustration
Two waves of same frequency but of amplitudes a and 2a respectively superimpose over each other. The amplitude at a point where the phase difference is \displaystyle \frac{{3\pi }}{2} will be
Solution
Here
\displaystyle a\,\,=\,\,\sqrt{{a_{1}^{2}+a_{2}^{2}\,\,+\,\,2{{a}_{1}}\,\,{{a}_{2}}\,\,\,\cos \,\,\phi }}
\displaystyle =\,\,\,\sqrt{{{{a}^{2}}\,\,+\,\,{{{(2a)}}^{2}}+2a\,\,\cdot \,\,2a\,\cdot \,\,\cos \,\,\frac{{3\pi }}{2}}}
= \displaystyle \sqrt{{{{a}^{2}}+4{{a}^{2}}+4{{a}^{2}}\times \,\,0}}
= \displaystyle \sqrt{{5\,\,{{a}^{2}}}}
= \displaystyle \sqrt{5}\,\,a
Illustration
Two coherent sound sources are at distances \displaystyle {{x}_{1}}= 0.2 m and \displaystyle {{x}_{2}}= 0.48 m from a point. Calculate the intensity of the resultant wave at that point if the frequency of each wave is 400 Hz and velocity of wave in the medium is v = 448 m/s. The intensity of each wave is \displaystyle {{I}_{o}} = 60 \displaystyle W/{{m}^{2}}?
Solution
Path difference, \displaystyle \Delta x={{x}_{2}}-{{x}_{1}}=0.48-0.2=0.28m
\displaystyle \phi =\frac{{2\pi }}{\lambda }\Delta x=\left( {\frac{{2\pi }}{{c/\nu }}} \right)\Delta x=\frac{{2\pi \left( {400} \right)\left( {0.28} \right)}}{{448}}=\frac{\pi }{2}
\displaystyle I={{I}_{1}}+{{I}_{2}}+2\sqrt{{{{I}_{1}}{{I}_{2}}}}\cos \phi
or \displaystyle I={{I}_{o}}+{{I}_{o}}+2{{I}_{o}}\cos \left( {\pi /2} \right)
\displaystyle =2{{I}_{o}}=2\left( {60} \right)=120\text{ }W/{{m}^{2}}
Illustration
Consider interference due to two coherent waves of same frequency and constant phase difference having intensities I and 4I, respectively. What is the resultant intensity when the phase difference between these two waves is \displaystyle \pi /2 and \displaystyle \pi ?
Solution
According to Eq.
\displaystyle I={{I}_{1}}+{{I}_{2}}+2\sqrt{{{{I}_{1}}{{I}_{2}}}}\cos \delta
Given : \displaystyle {{I}_{1}} =I and \displaystyle {{I}_{2}} =4I,
so I = 5 I + 2 I \displaystyle \sqrt{4}\ \cos \delta
= 5 I + 4 I \displaystyle \cos \delta
Hence \displaystyle {{I}_{{\pi /2}}}=5I+4I\cos 90{}^\circ =5I
\displaystyle {{I}_{\pi}}=5I + 4I \displaystyle \cos \pi = I
Illustration
A light source emits light of two wavelengths \displaystyle {{\lambda }_{1}}=4300{{A}^{o}} and \displaystyle {{\lambda }_{2}}=5100{{A}^{o}}. The source is used in a double slit interference experiment. The distance between the slit is 0.025 mm and between source and screen is 1.5 m. Calculate the separation between the third order bright fringes due to these two wavelengths.
Solution
D = 1.5 m , d = 0.025 mm , \displaystyle {{\lambda }_{1}}=4300{{A}^{o}}, \displaystyle {{\lambda }_{2}}=5100{{A}^{o}}
n = 3
\displaystyle {{x}_{1}} = \displaystyle \frac{{n{{\lambda }_{1}}D}}{d} & x2 = \displaystyle \frac{{n{{\lambda }_{2}}D}}{d}
\displaystyle {{x}_{2}}-{{x}_{1}} = \displaystyle \frac{{nD}}{d}({{\lambda }_{2}}-{{\lambda }_{1}})
= 1.44 cm.
Illustration
In young’s double slit experiment fringe width is found to be 0.4 mm. If the whole apparatus is immersed in water of refractive index 4/3 without disturbing the geometrical arrangement, find the new fringe width.
Solution
\displaystyle\beta = \displaystyle \frac{{\lambda D}}{d} and
\displaystyle\beta’ = \displaystyle \frac{{{\lambda }’D}}{d}
\displaystyle \frac{{{\beta }’}}{\beta }=\frac{{{\lambda }’}}{\lambda }=\frac{1}{\mu }
\displaystyle \beta ‘=\frac{\beta }{\mu }= 0.3 mm
Illustration
Interference fringes are produced by a double slit arrangement and a piece of plane parallel glass of refractive index 1.5 is interposed in one of the interfering beam. If the fringes are displaced through 30 fringe widths for light of wavelength \displaystyle 6\times {{10}^{{-5}}} cm, find the thickness of the plate.
Solution
If a transparent plate of thickness t and refractive index m is introduced in the path of one of the interfering waves, the entire fringe pattern shifts by
S = \displaystyle \frac{D}{d}(\mu – 1)t)
Now S = 30 \displaystyle\beta = 30 \displaystyle \frac{{D\lambda }}{d}
hence 30 \displaystyle \frac{{D\lambda }}{d}=\frac{D}{d}(\mu -1)t
so t = \displaystyle 3.6\times {{10}^{{-3}}}cm.
Illustration
Fringes are produced using light of wavelength \displaystyle \lambda=4800{{A}^{o}} in a double-slit experiment. One of the slits is covered by a thin plate of glass of refractive index 1.4 and other slit by another plate of glass of double the thickness and of refractive index 1.7. During this process, the central bright fringe shifts to a position originally occupied by the fifth bright fringe from the centre. Find the thickness of each glass plate.
Solution
Let \beta is the fringe width
Path difference = \displaystyle {{S}_{2}P}-{{S}_{1}P} = \displaystyle \frac{{xd}}{D}
New path difference = \displaystyle {{S}_{2}P}+\text{ }({{\mu }_{2}}-\text{ }1)\text{ }2t\text{ }-{{S}_{1}P}-\text{ }({{\mu }_{1}}-\text{ }1)\text{ }.\text{ }t
= \displaystyle \frac{{xd}}{D}+2({{\mu }_{2}}-1)t – ({{\mu}_{1}} – 1)t
For, zero order fringe occurs at a distance given by
\displaystyle \frac{{xd}}{D}+2({{\mu }_{2}}-1)t – ({{\mu}_{1}} – 1)t = 0
so x = \displaystyle \left[ {({{\mu }_{1}}-1)t-2({{\mu }_{2}}-1)t} \right]\frac{D}{d}
= \displaystyle \left[ {({{\mu }_{1}}-1)t-2({{\mu }_{2}}-1)t} \right]\frac{\beta }{\lambda } [ \because \beta = \displaystyle \frac{{\lambda D}}{d} ]
put x = 5 \displaystyle\beta ,
hence t = \displaystyle -2.4\times {{10}^{{-6}}} m (– ve sign indicates that shift would take place towards 2nd slit and hence x should have been – ve because t cannot be negative)
therefore t = 2.4 \displaystyle \mum and 2t = 4.8 \displaystyle \mum.
Illustration
A beam of light consisting of two wavelength 6500 \displaystyle {{A}^{o}} and 5200 \displaystyle {{A}^{o}} is used to obtain interference fringes in a Young’s double slit experiment what is the least distance from the centre maximum where the bright fringes due to both the wave lengths coincide?
The distance between the slit is 2mm and the distance between the plane of the slits and the screen is 120 cm.
Solution
\displaystyle \frac{{nD{{\lambda }_{1}}}}{d}=\frac{{mD{{\lambda }_{2}}}}{d}
\displaystyle \frac{n}{m}=\frac{{5200}}{{6500}}=\frac{4}{5}
x = \displaystyle \frac{{4\times 120\times 6500\times {{{10}}^{{-6}}}}}{{2/1000}}=1.56mm
Illustration
Two beams of light having intensities I and 4I interfere to produce a fringe pattern on the screen phase difference between the beams is \displaystyle \pi /2 at point A and \displaystyle \pi at point B. Then find the difference between resultant intensities at A & B.
Solution
Given \displaystyle {{I}_{1}}=I, & \displaystyle {{I}_{2}}=4I
\displaystyle {{I}_{A}}=\text{ }{{I}_{1}}+\text{ }{{I}_{2}} + 2 \displaystyle \sqrt{{{{I}_{1}}+{{I}_{2}}}}\cos \frac{\pi }{2} = 5I
\displaystyle {{I}_{B}}=\text{ }{{I}_{1}}+\text{ }{{I}_{2}}+ 2 \displaystyle \sqrt{{{{I}_{1}}{{I}_{2}}}}\cos \pi = I
\displaystyle {{I}_{A}}-{{I}_{B}}=4I
Illustration
In Young’s experiment wavelength of red light is \displaystyle 7.8\times {{10}^{{-8}}} cm and that of blue light is \displaystyle 5.2\times {{10}^{{-8}}}cm. Find the value of n for which \displaystyle {{(n+1)}^{{th}}} blue bright line coincides with nth red fringe.
Solution
As \displaystyle {{n}_{1}}{{\lambda }_{1}}=\text{ }{{n}_{2}}{{\lambda }_{2}}
\displaystyle \frac{{{{n}_{2}}}}{{{{n}_{1}}}}=\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}=\frac{{7.8\times {{{10}}^{{-8}}}}}{{5.2\times {{{10}}^{{-8}}}}}=\frac{3}{2}
also \displaystyle {{n}_{2}}\text{ }{{n}_{1}}=\text{ }1 i.e. \displaystyle {{n}_{1}}=\text{ 2}
Illustration
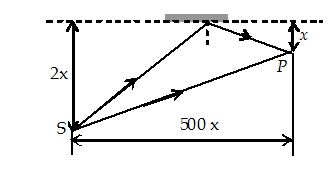
A vessel ABCD of 10cm width has two small slits {{S}_{1}} and {{S}_{2}} sealed with identical glass plates of equal thickness. The distance between the slits is 0.8 mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of {{S}_{1}} and {{S}_{2}}. A monochromatic light source is kept at S, 40cm below P and 2m from the vessel, to illuminate the slits as shown in the figure.
(a) Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ.
(b) Now, a liquid is poured into the vessel and filled up to OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid.
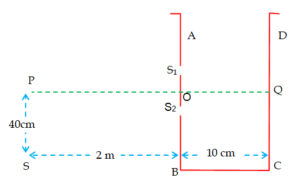
Solution
(a) For central maxima, optical path difference between the two rays must be zero. Also, since ( \displaystyle {{D}_{1}} and \displaystyle {{D}_{2}})>>d
\displaystyle \therefore d\text{ }sin\theta =\text{ }d\text{ }sin\alpha
\displaystyle \Rightarrow \text{ tan}\theta =\text{ tan}\alpha
\displaystyle \Rightarrow ~h/{{D}_{1} }=\text{ }x/{{D}_{2}}
therefore y = 2 cm
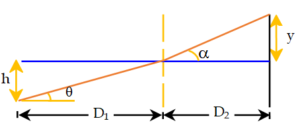
(b) \displaystyle (\mu -\text{ }1){{D}_{2}}=\text{ }d\text{ }sin\theta
solving we get, \displaystyle\mu = 1.0016.
Illustration
In a Young’s double slit experiment set-up, source S of wavelength 5000 \displaystyle {{A}^{o}} illuminates two slits {{S}_{1}} and {{S}_{2}}, which act as two coherent sources. The source S oscillates about its shown position according to the equation along y-axis, \displaystyle y=0.5\text{ }sin\pi t, where y is in millimeters and t in seconds.
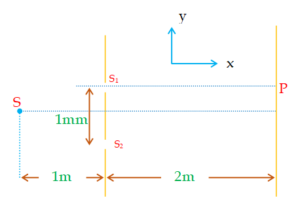
Find
(a) position of the central maxima as a function of time
(b) minimum value of t for which the intensity at point P on the screen exactly in front of the upper slit becomes maximum.
Solution
(a) For central maxima, path difference = 0
S{{S}_{2}} + {{S}_{2}}C – (S{{S}_{1}} + {{S}_{1}}C) = 0
Þ (S{{S}_{2}} – S{{S}_{1}}) + ({{S}_{2}}C – {{S}_{1}}C) = 0
Þ \displaystyle \frac{{dy}}{b}+\frac{{d{{y}_{1}}}}{D}=0
Þ \displaystyle {{y}_{1}}=\frac{{yD}}{b}
= – 2( \displaystyle 0.5sin\pi t) mm
\displaystyle {{y}_{1}}=- sin\pi t mm
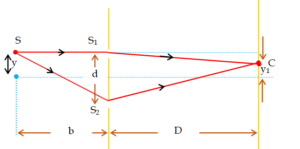
(b) Path difference \displaystyle \grave{\ }\Delta p’ at point P = S{{S}_{2}} – S{{S}_{1}} + ({{S}_{2}}P – {{S}_{1}}P)
\displaystyle \Delta p = \displaystyle \frac{{dy}}{b}+\frac{{d(d/2)}}{D} For intensity to be maximum
\displaystyle \Delta p=n\lambda
hence \displaystyle \frac{{dy}}{b}+\frac{{{{d}^{2}}}}{{2D}} = nl
Putting values, we get
0.5 ( \displaystyle sin\pi t) + 0.25 = 0.5 n
i.e. \displaystyle sin\pi t= \displaystyle \frac{{0.5n-0.25}}{{0.5}}
For minimum value of t, n = 1
hence t = \displaystyle \frac{1}{6} = 0.167 s.
Illustration
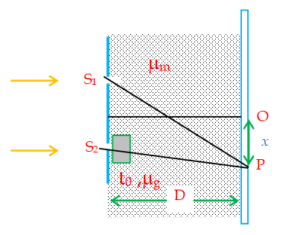
In a Young’s double slit experiment the region between the slits and the screen is filled with a liquid whose concentration starts changing at t = 0 and because of that its refractive index also changes with time as \displaystyle {{\mu }_{m}} = \displaystyle \frac{5}{2}-\frac{t}{4}. The final value of refractive index is found to be \displaystyle \frac{5}{4}. The separation between the slits is d = 2 mm and between the slit and screen is D = 1m. The thickness of glass plate shown in the figure is 36 \displaystyle\mu m and its refractive index is 1.5.
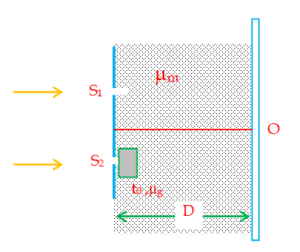
(a) Find the position of central maxima as a function of time and the time when it is at O.
(b) Find the speed of central maxima when it is at O.
Solution
(a) \displaystyle {{({{S}_{1}}P)}_{{OP}}} = \displaystyle {{\mu }_{m}} ({{S}_{1}}P)
\displaystyle {{({{S}_{2}}P)}_{{OP}}}= \displaystyle {{\mu }_{m}} ({{S}_{2}}P) \displaystyle +\text{ }({{\mu }_{g}}-{{\mu }_{m}}){{t}_{0}}
\ Optical path difference : \displaystyle {{(\Delta x)}_{{OP}}} = \displaystyle {{({{S}_{2}}P)}_{{OP}}} – \displaystyle {{({{S}_{1}}P)}_{{OP}}}
\displaystyle {{(\Delta x)}_{{OP}}}= \displaystyle {{\mu }_{m}} ({{S}_{2}}P – {{S}_{1}}P) + \displaystyle +\text{ }({{\mu }_{g}}-{{\mu }_{m}}){{t}_{0}}
\displaystyle {{(\Delta x)}_{{OP}}}= \frac{{{{\mu }_{m}}xd}}{D}+({{\mu }_{g}}-{{\mu }_{m}}){{t}_{0}}
For Central max., \displaystyle {{(\Delta x)}_{{OP}}}= 0
\ x = – \displaystyle \frac{{({{\mu }_{g}}-{{\mu }_{m}})}}{{{{\mu }_{m}}}}\frac{{{{t}_{0}}D}}{d}
x = \displaystyle \frac{{(4-t){{t}_{0}}D}}{{(10-t)d}} —-(a)
When at ‘O’, x = 0
\ t = 4 sec.
(b) To get the speed just differentiate x (equation (a)] w.r.t. time t and put t = 4 .
Speed of central max.
v = \displaystyle \left| {\frac{{dx}}{{dt}}} \right|=\frac{{6D{{t}_{0}}}}{{{{{(10-t)}}^{2}}d}}
When it is at O, t = 4 sec.
\displaystyle v=\frac{{6D{{t}_{0}}}}{{36d}}=\frac{{1\times 36\times 1\times {{{10}}^{{-6}}}}}{{6\times 2\times {{{10}}^{{-3}}}}}
= \displaystyle 3\times {{10}^{{-3}}}m/sec = 3 mm/sec.
Illustration
A point source S emitting light of wavelength 600 nm is placed at a very small height h above a flat reflecting surface AB (see figure). The intensity of the reflected light is 36% of the incident intensity. Interference fringes are observed on a screen placed parallel to the reflecting surface at a very large distance D from it.
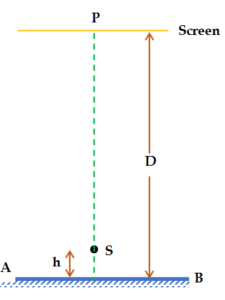
(a) What is the shape of the interference fringes on the screen?
(b) Calculate the ratio of the minimum to the maximum intensities in the interference fringes formed near the point P (shown in the figure).
(c) If the intensity at point P corresponds to a maximum, calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
Solution
(a) As there is symmetry about the line SP, fringes will be circular.
(b) \displaystyle \frac{{{{I}_{{\min }}}}}{{{{I}_{{\max }}}}}={{\left( {\frac{{\sqrt{I}-\sqrt{{0.36I}}}}{{\sqrt{I}+\sqrt{{0.36I}}}}} \right)}^{2}}={{\left( {\frac{{0.4}}{{1.6}}} \right)}^{2}}=\frac{1}{{16}}
(c) For maximum at P, path difference = \displaystyle n\lambda .
If AB is shifted by a distance x, it will cause an additional path difference of 2x.
2x = \displaystyle \lambda (for minimum value of x)
Þ x = \displaystyle \lambda /2 = 300 nm
Illustration
Find the maximum intensity in case of interference of n identical waves each of intensity I0 if the interference is
(i) coherent (ii) incoherent
Solution
(i) In case of two coherent sources, \displaystyle {{I}_{R}}={{I}_{1}}+{{I}_{2}} + 2 \sqrt{{{{I}_{1}}{{I}_{2}}}} \displaystyle \cos \phi
\displaystyle {{I}_{R}} will be maximum when \displaystyle \cos \phi = maximum = 1
\displaystyle \therefore {{\left( {{{I}_{{max}}}} \right)}_{{co}}}={{I}_{1}}+{{I}_{2}} + 2 \sqrt{{{{I}_{1}}{{I}_{2}}}} = {{\left( {\sqrt{{{{I}_{1}}}}+\,\sqrt{{{{I}_{2}}}}} \right)}^{2}}
So for n identical waves each of intensity \displaystyle {{I}_{o}},
\displaystyle {{\left( {{{I}_{{max}}}} \right)}_{{co}}} = ( \sqrt{{{{I}_{0}}}}\,+\,\sqrt{{{{I}_{0}}}} … )2 = (n \sqrt{{{{I}_{0}}}})2 = \displaystyle {{n}^{2}}{{I}_{0}}
(ii) In case of incoherent sources,
\displaystyle {{I}_{R}}={{I}_{1}}+{{I}_{2}}+…. +{{I}_{n}}
= \displaystyle {{I}_{0}}+\text{ }{{I}_{0}}+ …(n times) = \displaystyle n{{I}_{o}}
Practice Questions (JEE Main Level)
1.
In the Young’s double slit experiment apparatus shown in figure, the ratio of maximum to minimum intensity on the screen is 9. The wavelength of light used is \displaystyle \lambda , then the value of Y is :
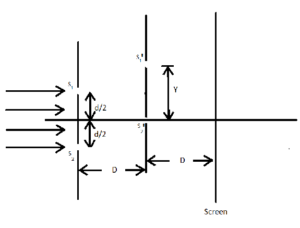
(a) \displaystyle \frac{{\lambda D}}{d}
(b) \displaystyle \frac{{\lambda D}}{{2d}}
(c) \displaystyle \frac{{\lambda D}}{{3d}}
(d) \displaystyle \frac{{\lambda D}}{{4d}}
Ans (d)
2.
The maximum intensity in Young’s double slit experiment is Io. Distance between the silts is d = 5 \displaystyle \lambda , where \displaystyle \lambda is the wavelength of monochromatic light used in the experiment. What will be the intensity of light in front of one of the slits on a screen at a distance D = 10 d?
(a) \displaystyle \frac{{{{I}_{o}}}}{2}
(b) \displaystyle \frac{3}{4}{{I}_{o}}
(c) \displaystyle {{I}_{o}}
(d) \displaystyle \frac{{{{I}_{o}}}}{4}
Ans (a)
3.
When one of the slits of Young’s experiment is covered with a transparent sheet of thickness 4.8 mm, the central fringe shifts to a position originally occupied by the 30th bright fringe. What should be the thickness of the sheet if the central fringe has to shift to the position occupied by 20th bright fringe?
(a) 3.8 mm
(b) 1.6 mm
(c) 7.6 mm
(d) 3.2 mm
Ans (d)
4.
In the ideal double-slit experiment, when a glass plate ( \displaystyle \mu = 1.5) of thickness t is introduced in the path of one of the intersecting beams (wavelength \displaystyle \lambda ) the intensity at the position where the central maximumoccurred previously remains unchanged. The minimum thickness of the glass plate is?
(a) 2 \displaystyle \lambda
(b) 2 \displaystyle \lambda /3
(c) \displaystyle \lambda /3
(d) \displaystyle \lambda
Ans (a)
5.
In the Young’s double slit experiment a point P on the central bright fringe is such that intensity of point P is 1/4 times the maximum intensity, distance between the slits is d and wavelength \displaystyle \lambda . Then angular separation of point P is
(a) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{d}} \right)
(b) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{{2d}}} \right)
(c) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{{3d}}} \right)
(d) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{{4d}}} \right)
Ans (c)
6.
In an interference arrangement similar to Young’s double-slit experiment, the slits and are illuminated with coherent microwave sources, each of frequency Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d=150.0m. The intensity I\left( \theta \right) is measured as a function of \theta , where \theta is defined as shown. If {{I}_{0}} is the maximum intensity, then I\left( \theta \right) for 0\le \theta \le 90{}^\circ is given by
(a) I\left( \theta \right)={{I}_{0}}/2for \theta =30{}^\circ
(b) I\left( \theta \right)={{I}_{0}}/4for \theta =90{}^\circ
(c) I\left( \theta \right)={{I}_{0}}for \theta =0{}^\circ
(d) I\left( \theta \right)is constant for all values of \theta
Ans (b)
7.
In a double slit experiment instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
(a) the intensities of both the maxima and the minima increase
(b) the intensity of the maxima increases and the minima has zero intensity
(c) the intensity of the maxima decreases and that of the minima increases
(d) the intensity of the maxima decrease and the minima has zero intensity
Ans (d)
8.
Two beams of light having intensities I and \displaystyle 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is \pi /2 at point and \pi at point . Then the difference between the resultant intensities at and is
(a) \displaystyle 4I
(b) \displaystyle 4I
(c) \displaystyle 5I
(d) \displaystyle 7I
Ans (c)
9.
In a Young’s double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600 nm is used. If the wavelength of light is changed to 400 nm, number of fringes observed in the same segment of the screen is given by
(a) 12
(b) 18
(c) 24
(d) 30
Ans (d)
10.
White light is used to illuminate the two slits in Young’s Double Slit experiment. The separation between the slits is b and the screen is at a distance d(>> b) from the slits. At a point on the screen directly in front of any of the slits, certain wavelength are missing. Some of these missing wavelength are
(a) \displaystyle \lambda \,=\,\frac{{{{b}^{2}}}}{d}
(b) \displaystyle \lambda \,=\,\frac{{{{b}^{2}}}}{{3d}}
(c) Both (a) and (b)
(d) \displaystyle \lambda \,=\,\frac{{2{{b}^{2}}}}{{3d}}
Ans (c)
11.
A thin slice is cut out of a glass cylinder along a plane parallel to its axis. The slice is placed on a flat glass plate as shown. The observed interference fringes from this combination shall be
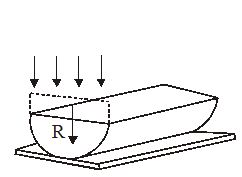
(a) straight
(b) circular
(c) equally spaced
(d) having fringe spacing which increases as we go outwards
Ans (d)
12.
In Young’s experiment, let P and Q be the two slits. A thin film of thickness t and refractive index n is placed in front of P. If \displaystyle \beta be the fringe width and \displaystyle \lambda be the wavelength of light then the central maxima will shift
(a) towards \displaystyle P\,\,\,by\,\,\,t(n1)\frac{\beta }{\lambda }
(b) towards \displaystyle Q\,\,by\,\,t(n1)\frac{\beta }{\lambda }
(c) towards \displaystyle P\,\,by\,\,nt\frac{\beta }{\lambda }
(d) towards \displaystyle Q\,\,by\,\,nt\frac{\beta }{\lambda }
Ans (a)
13.
Light of wavelength \displaystyle {{\lambda }_{0}}in air enters a medium of refractive index n. If two points A and B in this medium lie along the path of this light at a distance x, then phase difference \displaystyle {{\varnothing }_{0}} between these two points is
(a) \displaystyle {{\phi }_{0}}\,=\,\frac{1}{n}\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
(b) \displaystyle {{\phi }_{0}}\,=\,n\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
(c) \displaystyle {{\phi }_{0}}\,=\,(n1)\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
(d) \displaystyle {{\phi }_{0}}\,=\,\frac{1}{{(n1)}}\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
Ans (b)
14.
In Young’s double slit experiment, the slits are 2 mm apart and are illuminated with a mixture of two wavelengths \displaystyle {{\lambda }_{o}}\,=\,750\,nm\,\,\,and\,\,\lambda \,=\,900\,nm. The minimum distance from the common central bright fringe on a screen 2 m from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other is
(a) 1.5 mm
(b) 3 mm
(c) 4.5 mm
(d) 6 mm
Ans (c)
15.
In the ideal double slit experiment, when a glass plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength \displaystyle \lambda ) the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass plate is
(a) 2 \displaystyle \lambda
(b) \displaystyle \frac{{2\lambda }}{3}
(c) \displaystyle \frac{\lambda }{3}
(d) \displaystyle \lambda
Ans (a)
16.
Two wavelengths of light \displaystyle {{\lambda }_{1}} and \displaystyle {{\lambda }_{2}} are sent through a Young’s double slit apparatus simultaneously. If the third order l1 bright fringe coincides with the fourth order \displaystyle {{\lambda }_{2}}bright fringe then
(a) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{4}{3}
(b) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{3}{4}
(c) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{5}{4}
(d) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{4}{5}
Ans (a)
17.
Two identical sources each of intensity Iohave a separation \displaystyle d\,=\,\frac{\lambda }{8}, where \displaystyle \lambda is the wavelength of the waves emitted by either source. The phase difference of the sources is \displaystyle \frac{\pi }{4}. The intensity distribution I(q) in the radiation filed as a function of[ \displaystyle \theta ], which specifies the direction from the sources to the distant observation point P is given by
(a) \displaystyle I\,(\theta )\,=\,{{I}_{o}}\,{{\cos }^{2}}\,\theta
(b) \displaystyle I\,(\theta )\,=\,\frac{{{{I}_{o}}}}{4}\,{{\cos }^{2}}\,\left( {\frac{{\pi \theta }}{8}} \right)
(c) \displaystyle I\,(\theta )\,=\,4{{I}_{o}}{{\cos }^{2}}\,\left( {\frac{\pi }{8}\,(\sin \theta \,+\,1)} \right)
(d) \displaystyle I\,(\theta )\,=\,{{I}_{o}}{{\sin }^{2}}\,\theta
Ans (c)
18.
In a double slit experiment, instead of taking slits of equal widths, one slit is made twice as wide as the other. Then in the interference pattern
(a) the intensities of both the maxima and the minima increase
(b) the intensity of the maxima increases and minima has zero intensity
(c) the intensity of the maxima decreases and that of minima increases
(d) the intensity of the maxima decreases and the minima has zero intensity
Ans (a)
19.
In a Fresnel biprism set-up, l is the distance of the prism from the source slit, A is the angle of the prism and \displaystyle \mu is the refractive index of the material of the prism. Then the separation between the two virtual sources will be equal to
(a) lA ( \displaystyle \mu – 1)/2
(b) 2lA ( \displaystyle \mu – 1)
(c) 3lA ( \displaystyle \mu – 1)
(d) 4lA( \displaystyle \mu – 1)
Ans (c)
20.
Consider a usual set up of Young’s double slit experiment with slits of equal intensity as shown in the figure. Take ‘O’ as origin and the Y axis as indicated. If average intensity between y1 = – \displaystyle \frac{{\lambda D}}{{4d}} and y2 = + \displaystyle \frac{{\lambda D}}{{4d}} equals ‘n’ times the intensity of maxima, then ‘n’ equals
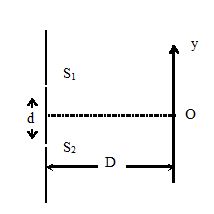
(a) \displaystyle \frac{1}{2}\left( {1+\frac{2}{\pi }} \right)
(b) \displaystyle 2\left( {1+\frac{2}{\pi }} \right)
(c) \displaystyle \left( {1+\frac{2}{\pi }} \right)
(d) \displaystyle \frac{1}{2}\left( {1-\frac{2}{\pi }} \right)
Ans (a)
21.
In a Young’s double slit experiment, the fringes are displaced by a distance ‘x’ when a glass plate of refractive index 1.5 is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is (3/2)x. The refractive index of second plate is
(a) 1.75
(b) 1.50
(c) 1.25
(d) 1.00
Ans (c)
22.
Which of the following is not an essential condition for interference
(a) The two interfering waves must be propagated in almost the same direction or the two interfering waves must intersect at very small angle
(b) The waves must have the same period and wavelength
(c) The amplitude of the two waves must be equal
(d) The two interfering beams of light must originate from the same source
Ans (c)
23.
To demonstrate the phenomenon of interference we require
(a) two sources which emit radiation’s of the same frequency
(b) two sources which emit radiations of nearly the same frequency
(c) two sources which emit radiations of the same frequency and have a definite phase relationship
(d) two sources which emit radiations of different frequencies
Ans (c)
24.
A bright fringe in Young’s double-slit experiment is 1.5 cm from the center of the pattern. The light has a wave length of 612 nm and falls on a screen 1.4 m from the slits, whose separation is 0.4 mm. How many dark fringes are there between the center and the bright fringe at 1.5 cm?
(a)5 fringes
(b)7 fringes
(c)10 fringes
(d)2 fringes
Ans (b)
25.
Light of wavelength 627 nm illuminates two slits. What is the minimum path difference between the waves from the slits for the resultant intensity to fall to 25% of the central maximum?
(a)200nm
(b)205 nm
(c)209 nm
(d)215 nm
Ans (c)
26.
In a Young’s double slit experiment, two wavelengths of 500 nm and 700 nm were used. What is the minimum distance from the central maximum where their maximas coincide again? Take D/d = 103. Symbols have their usual meanings.
(a)5.0 mm
(b)3.5 mm
(c)2.0 mm
(d)3.0 mm
Ans (b)
Practice Questions (JEE Advance Level)
Comprehension Based Question (1 to 3)
Plane waves are incident on a pair of slits at angle a, as shown in figure.
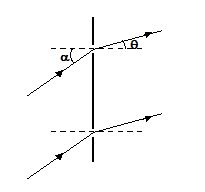
1.
What is the path difference between the rays leaving at angle q as shown? (The screen is far away).
(a)d(sinΘ – sinα)
(b)d(sinΘ + sinα)
(c) (sinΘ – sinaα)
(d)d(sinΘ – sin0)
Ans (a)
2.
At what value of q is the central peak located?
(a) Θ = 0
(b) Θ = α
(c) Θ = 5
(d) Θ = 1
Ans (b)
3.
What is the minimum value of a for which the intensity at the centre of the screen is a minimum?
(a) sin-2(λ/2d)
(b) sin-1(λ/2d)
(c) sin-3(λ/2d)
(d) sin-5(λ/2d)
Ans (b)
4.
A vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between the slits is 0.8 mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S, 40 cm below P and 2 m from the vessel, to illuminate the slits as shown in the figure below. Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ. Now, a liquid is poured into the vessel and filled uptoOQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid.
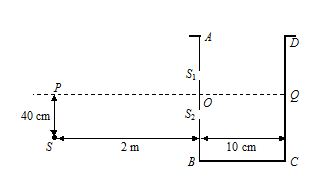
(a)5 cm, 1.0020
(b)2 cm, 1.0016
(c)6 cm, 1.0050
(d)2 cm, 1.05
Ans (b)
Comprehension Based Question (5 and 6)
In the arrangement shown in the figure, light of wavelength 6000 Å is incident on slits S1 and S2. Slits S3 and S4 have been opened such that S3 is the position of first maximum above the central maximum and S4 is the position where intensity is same as that of the light used, below the central maximum closest to it. The point O is equidistant from S1&S2 and O¢ is equidistant from S3&S4. The intensity of incident light is Io.
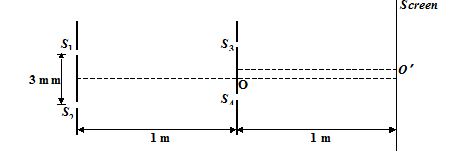
5.
the intensity at O¢ (on the screen) and
(a) 3{{I}_{o}}
(b) 1{{I}_{o}}
(c) 5{{I}_{o}}
(d) 2{{I}_{o}}
Ans (a)
6.
intensity of brightest fringe.
(a) 6{{I}_{o}}
(b) 9{{I}_{o}}
(c) 3{{I}_{o}}
(d) 2{{I}_{o}}
Ans(b)
