Video Lecture
Theory For Making Notes





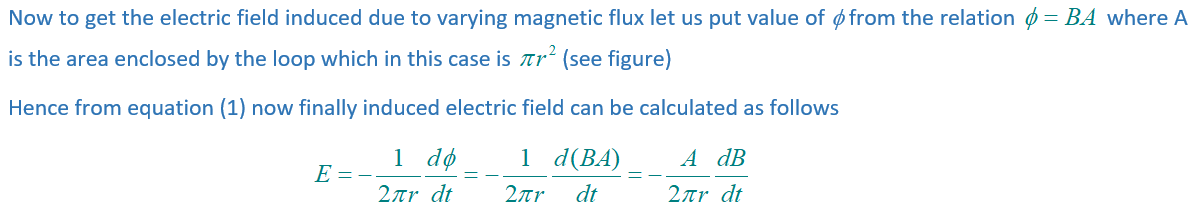

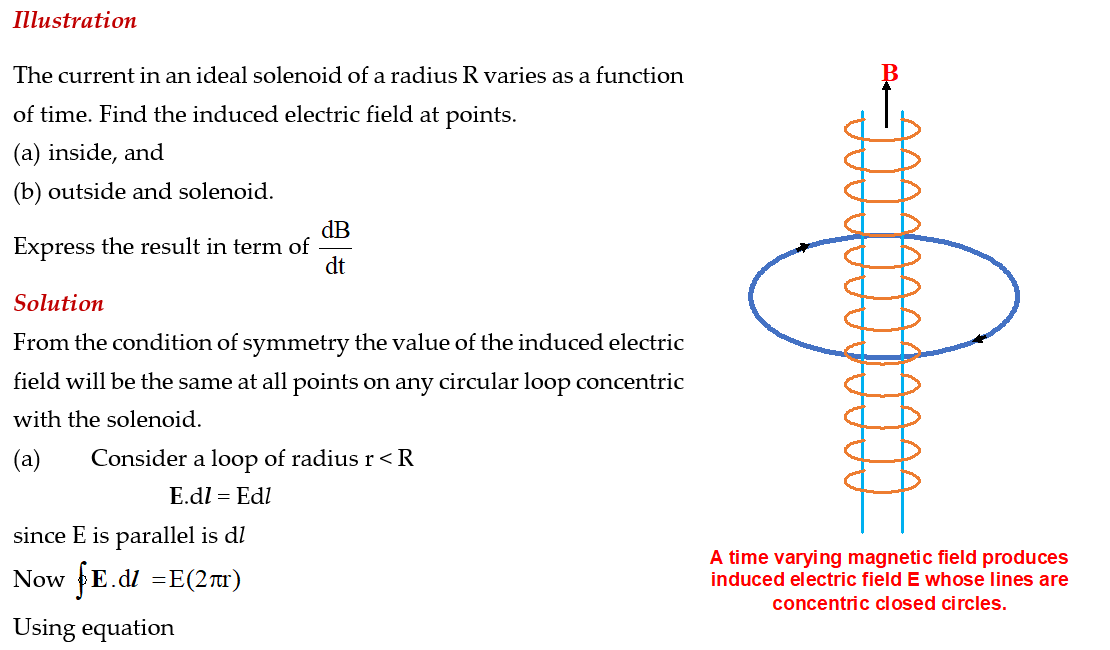
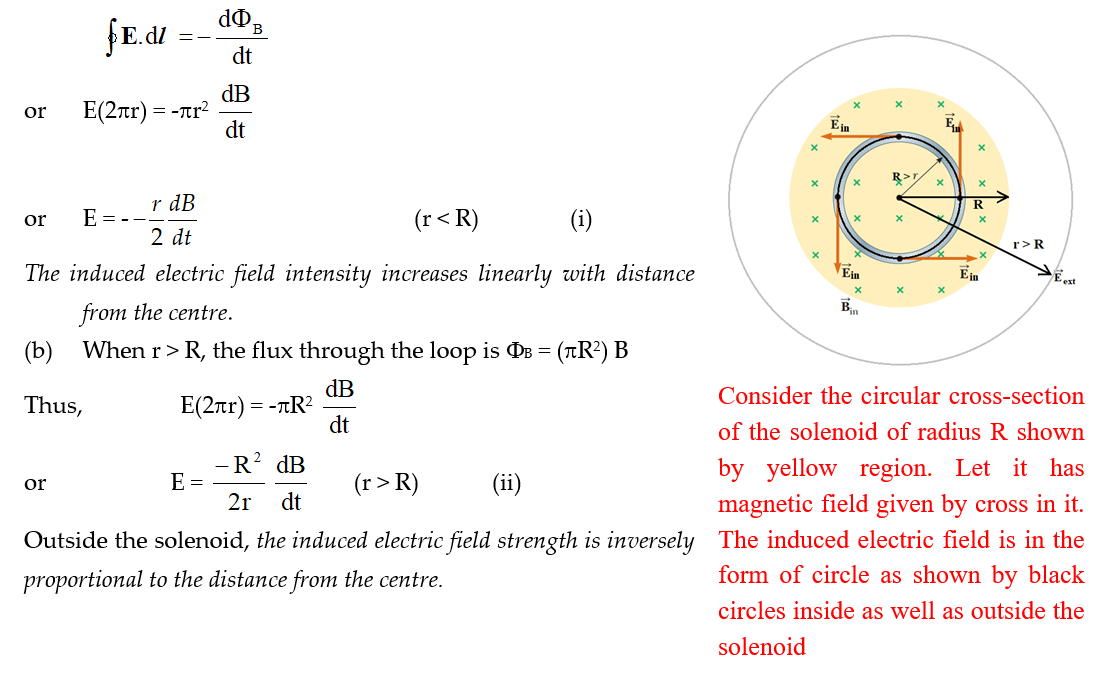
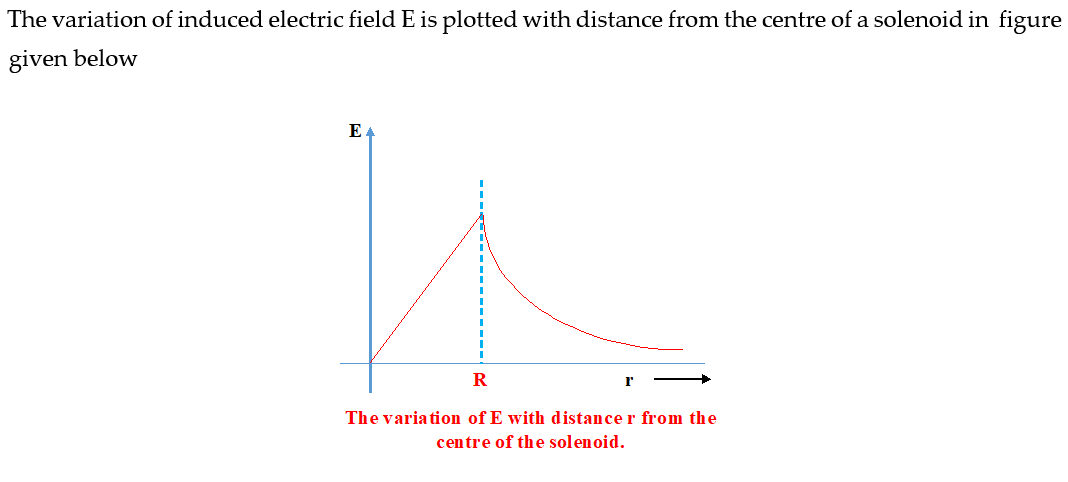
Practice Questions (Level-1)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-2)
Q.1
Figure shows two coils made from the same wire and of radii a and b. They are placed in a magnetic field perpendicular to their plane which varies as B = Bo sin wt. If the resistance of the two coils be R, then what is current in the loop?
(a) \frac{{\omega {{B}_{o}}\cos \omega t}}{R}
(b) \frac{{\omega \pi \left( {{{a}^{2}}-{{b}^{2}}} \right)}}{R}{{B}_{o}}\cos \omega t
(c) \frac{{\pi \left( {{{a}^{2}}-{{b}^{2}}} \right)}}{R}{{B}_{o}}\cos \omega t
(d) \frac{{\omega \pi \left( {{{a}^{2}}+{{b}^{2}}} \right)}}{R}{{B}_{o}}\cos \omega t
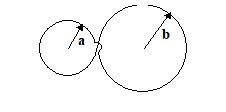
Ans. (b)
Q.2
An equilateral triangular loop having a resistance R and length of each side l is placed in a magnetic field which is varying at \frac{{dB}}{{dt}}=1\,T/S. The induced current in the loop will be
(a) \frac{{\sqrt{3}}}{4}\frac{{{{l}^{2}}}}{R}
(b) \frac{4}{{\sqrt{3}}}\frac{{{{l}^{2}}}}{R}
(c) \frac{{\sqrt{3}}}{4}\frac{R}{{{{l}^{2}}}}
(d) \frac{4}{{\sqrt{3}}}\frac{R}{{{{l}^{2}}}}
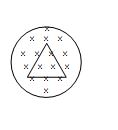
Ans. (a)
Q.3
A conducting circular loop is placed in a uniform magnetic field of induction B tesla with its plane normal to the field. Now the radius of the loop starts shrinking at the rate (dr/dt). Then the induced e.m.f. at the instant when the radius is r will be
(a) \pi rB\left( {\frac{{dr}}{{dt}}} \right)
(b) 2\pi rB\left( {\frac{{dr}}{{dt}}} \right)
(c) \pi {{r}^{2}}\left( {\frac{{dB}}{{dt}}} \right)
(d) B\frac{{\pi {{r}^{2}}}}{2}\frac{{dr}}{{dt}}
Ans. (b)
Q.4
A uniform but time varying magnetic field exists in cylindrical region and directed into the paper. If field decreases with time and a positive charge placed at any point inside the region, then it moves
(a) along 1 (b) along 2 (c) along 3 (d) along 4
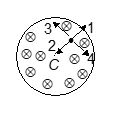
Ans. (c)
Q.5
A uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the paper and the magnitude of the field is increasing at a constant rate a. There is a straight conducing rod of length 2R placed as shown in the figure. The magnitude of induced emf across the rod is
(a) pR2a
(b) \frac{{\pi {{R}^{2}}\alpha }}{2}
(c) \frac{{{{R}^{2}}\alpha }}{{\sqrt{2}}}
(d) \frac{{\pi {{R}^{2}}\alpha }}{4}
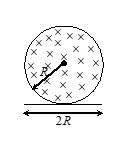
Ans. (d)
Q.6
A uniform magnetic field is confined in a cylindrical region of radius R. If the magnetic field is increased at a constant rate, then the variation of electric field (E) with the distance (r) from the axis of cylindrical region can best represented by
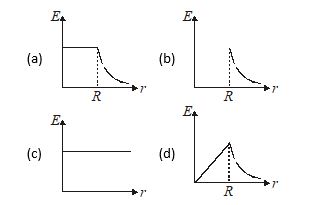
Ans. (d)
