Video Lecture
Theory For Making Notes





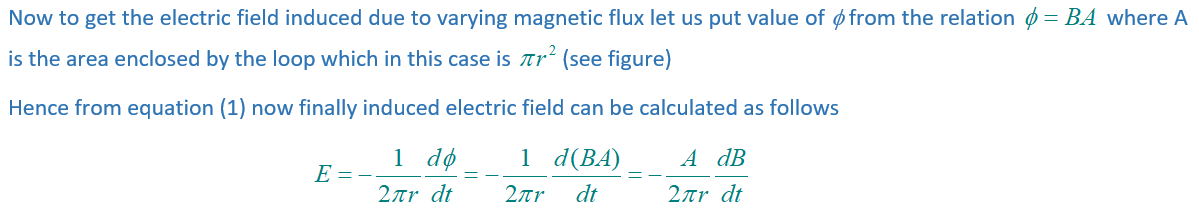

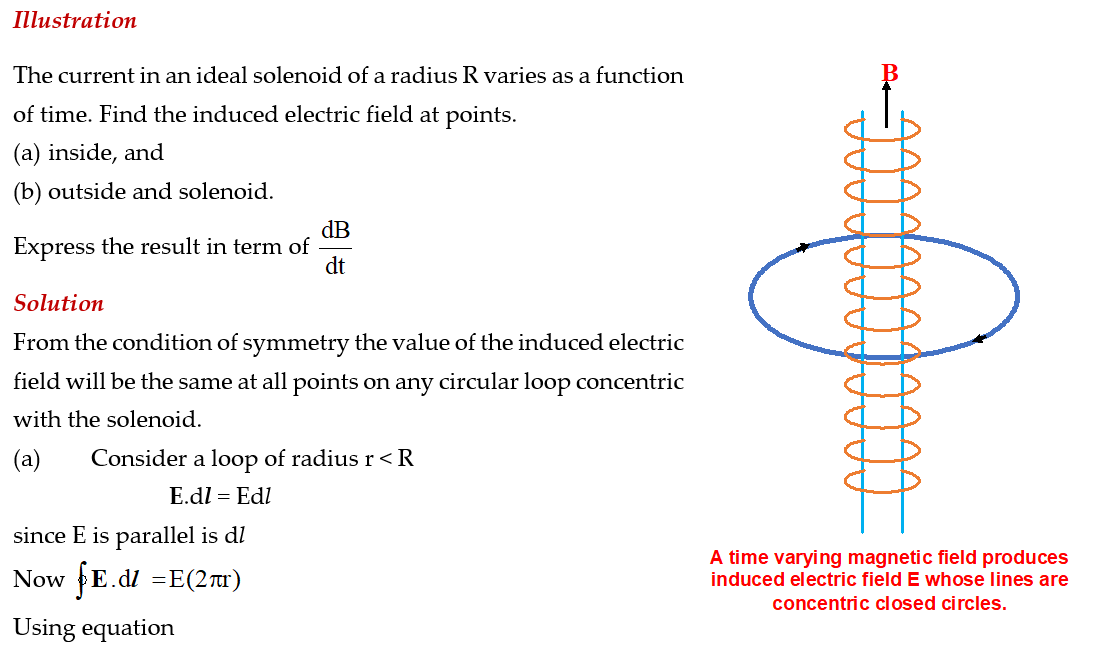
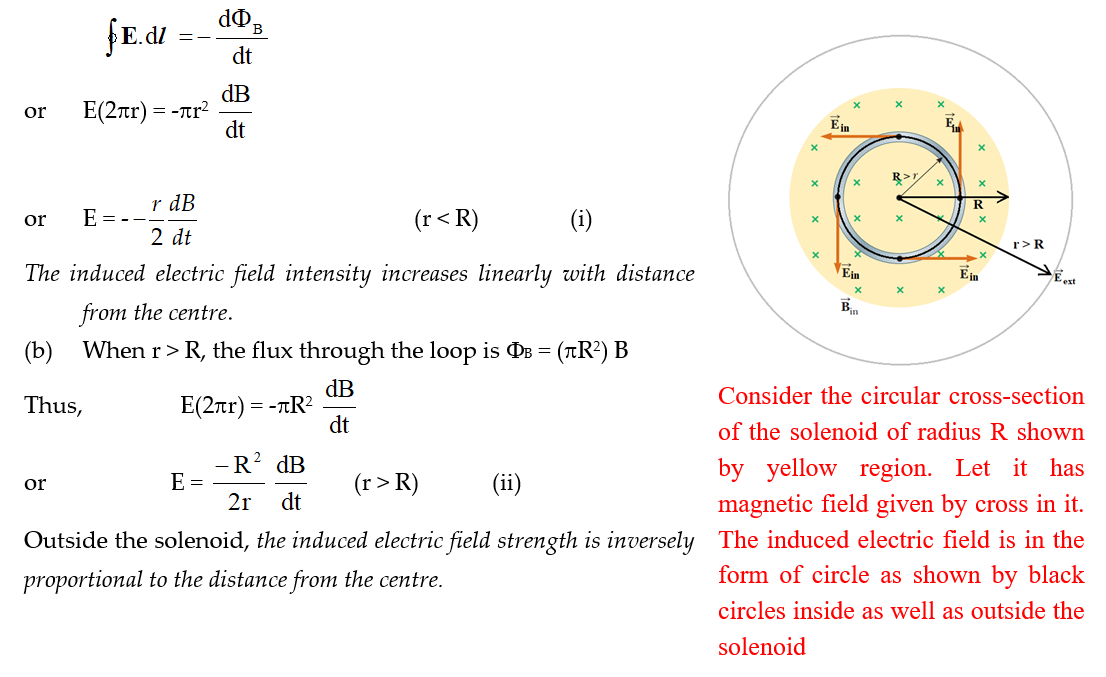
Practice Questions (Basic Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Main Level)
Q.1
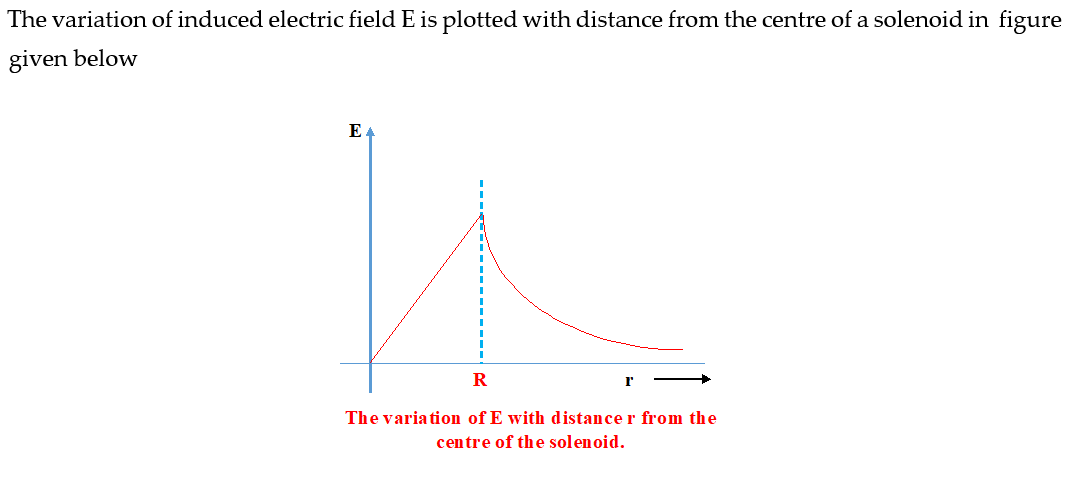
Figure shows two coils made from the same wire and of radii a and b. They are placed in a magnetic field perpendicular to their plane which varies as B = Bo sin wt. If the resistance of the two coils be R, then what is current in the loop?
(a) \frac{{\omega {{B}_{o}}\cos \omega t}}{R}
(b) \frac{{\omega \pi \left( {{{a}^{2}}-{{b}^{2}}} \right)}}{R}{{B}_{o}}\cos \omega t
(c) \frac{{\pi \left( {{{a}^{2}}-{{b}^{2}}} \right)}}{R}{{B}_{o}}\cos \omega t
(d) \frac{{\omega \pi \left( {{{a}^{2}}+{{b}^{2}}} \right)}}{R}{{B}_{o}}\cos \omega t
Ans. (b)
Q.2
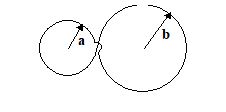
An equilateral triangular loop having a resistance R and length of each side l is placed in a magnetic field which is varying at \frac{{dB}}{{dt}}=1\,T/S. The induced current in the loop will be
(a) \frac{{\sqrt{3}}}{4}\frac{{{{l}^{2}}}}{R}
(b) \frac{4}{{\sqrt{3}}}\frac{{{{l}^{2}}}}{R}
(c) \frac{{\sqrt{3}}}{4}\frac{R}{{{{l}^{2}}}}
(d) \frac{4}{{\sqrt{3}}}\frac{R}{{{{l}^{2}}}}
Ans. (a)
Q.3
A conducting circular loop is placed in a uniform magnetic field of induction B tesla with its plane normal to the field. Now the radius of the loop starts shrinking at the rate (dr/dt). Then the induced e.m.f. at the instant when the radius is r will be
(a) \pi rB\left( {\frac{{dr}}{{dt}}} \right)
(b) 2\pi rB\left( {\frac{{dr}}{{dt}}} \right)
(c) \pi {{r}^{2}}\left( {\frac{{dB}}{{dt}}} \right)
(d) B\frac{{\pi {{r}^{2}}}}{2}\frac{{dr}}{{dt}}
Ans. (b)
Q.4
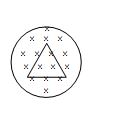
A uniform but time varying magnetic field exists in cylindrical region and directed into the paper. If field decreases with time and a positive charge placed at any point inside the region, then it moves
(a) along 1 (b) along 2 (c) along 3 (d) along 4
Ans. (c)
Q.5
A uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the paper and the magnitude of the field is increasing at a constant rate a. There is a straight conducing rod of length 2R placed as shown in the figure. The magnitude of induced emf across the rod is
(a) pR2a
(b) \frac{{\pi {{R}^{2}}\alpha }}{2}
(c) \frac{{{{R}^{2}}\alpha }}{{\sqrt{2}}}
(d) \frac{{\pi {{R}^{2}}\alpha }}{4}
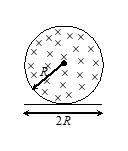
Ans. (d)
Q.6
A uniform magnetic field is confined in a cylindrical region of radius R. If the magnetic field is increased at a constant rate, then the variation of electric field (E) with the distance (r) from the axis of cylindrical region can best represented by
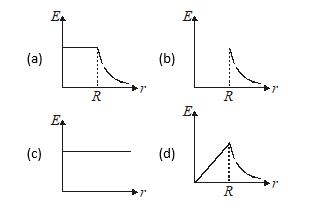
Ans. (d)
Practice Questions (JEE Advance Level)
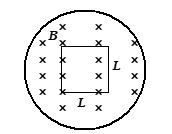
Q.1
Figure shows a square loop of side L perpendicular to the uniform field of a solenoid. Evaluate \oint{{\vec{E}}}. d \vec{l} around the loop.
(a) 4L\frac{{dB}}{{dt}}
(b) 2{{L}^{2}}\frac{{dB}}{{dt}}
(c) L\frac{{dB}}{{dt}}
(d) {{L}^{2}}\frac{{dB}}{{dt}}
Ans : (d)
Q.2
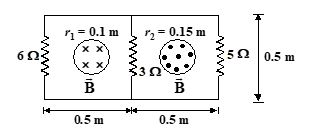
Two infinitely long solenoids (shown in cross-section) pass through a circuit as shown in the figure.
The magnitude of B inside each is the same and is increasing at the rate of
100 T/s. The current in 6ohm, 5ohm and 3ohm resistors are respectively
(a) 0.06A, 0.85A, 0.91A
(b) 2.06A, 1.85A,1.91A
(c) 0.06A, 2.85A,3.91A
(d) 1.06A, 0.85A,2.91A
Ans : (a)